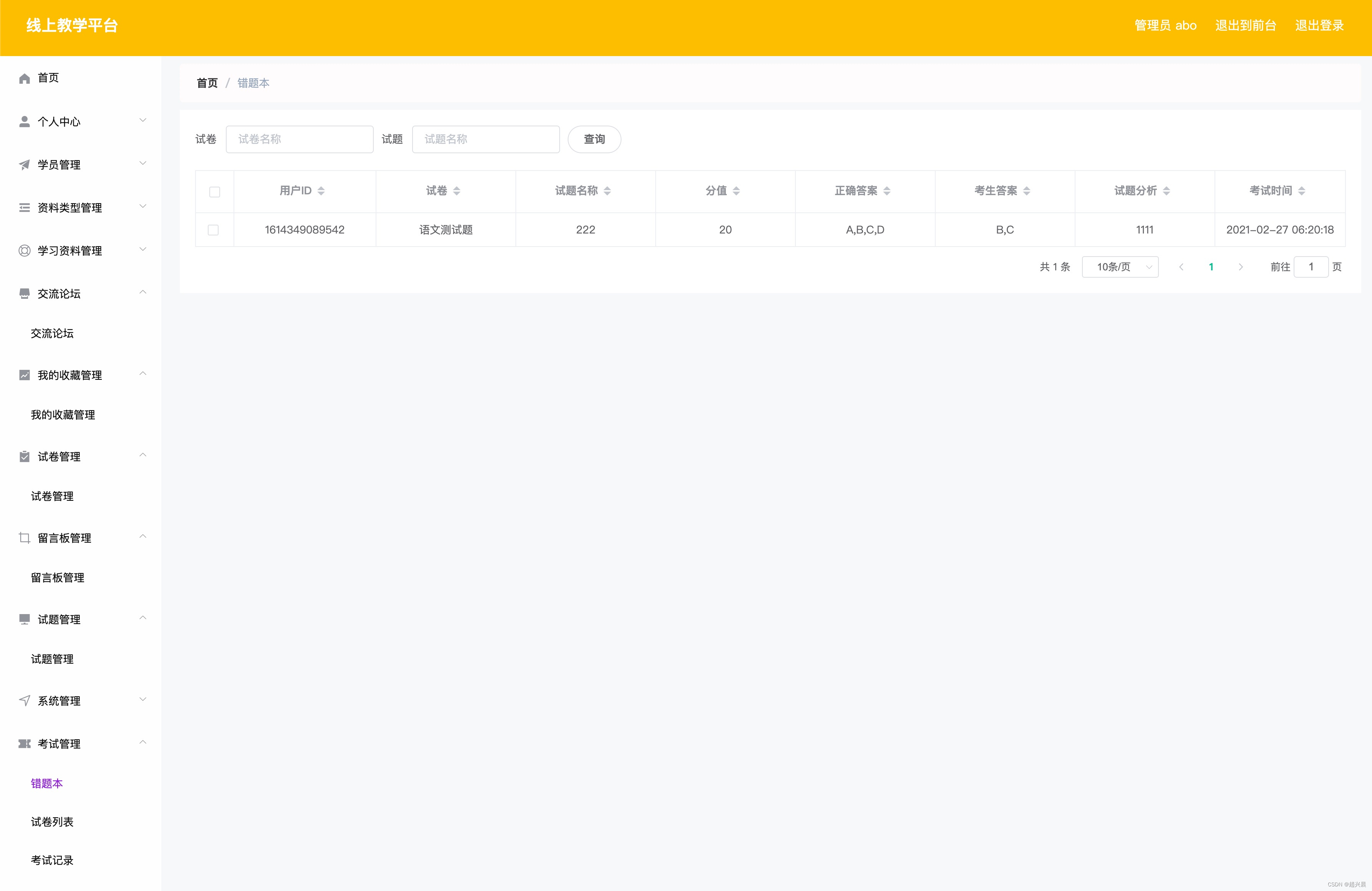
目录
- 第 9 周 17、 大规模机器学习(Large Scale Machine Learning)
- 17.3 小批量梯度下降
- 17.4 随机梯度下降收敛
第 9 周 17、 大规模机器学习(Large Scale Machine Learning)
17.3 小批量梯度下降
小批量梯度下降算法是介于批量梯度下降算法和随机梯度下降算法之间的算法,每计算常数𝑏次训练实例,便更新一次参数 𝜃 。
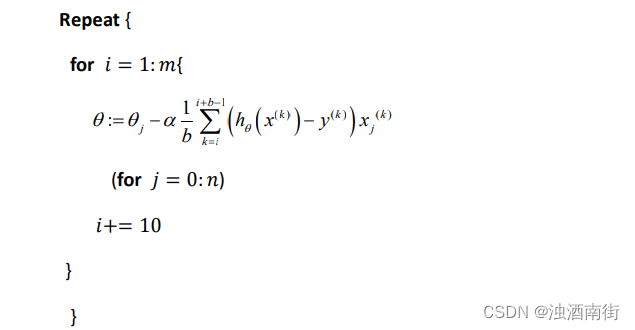
通常我们会令 𝑏 在 2-100 之间。这样做的好处在于,我们可以用向量化的方式来循环𝑏个训练实例,如果我们用的线性代数函数库比较好,能够支持平行处理,那么算法的总体表现将不受影响(与随机梯度下降相同)。
17.4 随机梯度下降收敛
现在我们介绍随机梯度下降算法的调试,以及学习率 𝛼 的选取。
在批量梯度下降中,我们可以令代价函数𝐽为迭代次数的函数,绘制图表,根据图表来判断梯度下降是否收敛。但是,在大规模的训练集的情况下,这是不现实的,因为计算代价太大了。
在随机梯度下降中,我们在每一次更新 𝜃 之前都计算一次代价,然后每𝑥次迭代后,求出这𝑥次对训练实例计算代价的平均值,然后绘制这些平均值与𝑥次迭代的次数之间的函数图表。
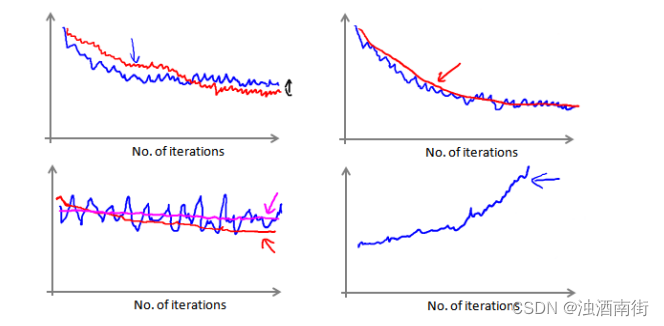
当我们绘制这样的图表时,可能会得到一个颠簸不平但是不会明显减少的函数图像(如上面左下图中蓝线所示)。我们可以增加𝛼来使得函数更加平缓,也许便能看出下降的趋势了(如上面左下图中红线所示);或者可能函数图表仍然是颠簸不平且不下降的(如洋红色线所示),那么我们的模型本身可能存在一些错误。
如果我们得到的曲线如上面右下方所示,不断地上升,那么我们可能会需要选择一个较小的学习率𝛼。
我们也可以令学习率随着迭代次数的增加而减小,例如令:
α = c o n s t 1 i t e r a t i o n N u m b e r + c o n s t 2 α=\frac{const_1}{iterationNumber + const_2} α=iterationNumber+const2const1
随着我们不断地靠近全局最小值,通过减小学习率,我们迫使算法收敛而非在最小值附近徘徊。 但是通常我们不需要这样做便能有非常好的效果了,对𝛼进行调整所耗费的计算通常不值得
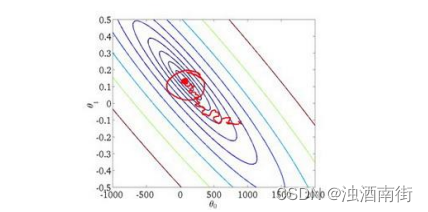
总结下,这段视频中,我们介绍了一种方法,近似地监测出随机梯度下降算法在最优化代价函数中的表现,这种方法不需要定时地扫描整个训练集,来算出整个样本集的代价函数,而是只需要每次对最后 1000 个,或者多少个样本,求一下平均值。应用这种方法,你既可以保证随机梯度下降法正在正常运转和收敛,也可以用它来调整学习速率𝛼的大小。