动量梯度下降算法(Momentum)是利用指数加权移动平均的思想来实现梯度下降的算法。让我们先来回顾一下基础的梯度下降方法以及看看它有哪些不足之处。接着引出动量梯度下降算法,在理解了它的原理后看看它是如何规避之前方法的不足的。
如果不知道指数加权平均是什么?可以看看我上一篇文章:
【机器学习300问】80、指数加权平均数是什么?![]() http://t.csdnimg.cn/4tFBg
http://t.csdnimg.cn/4tFBg
一、通过举例来感性认识
(1)基础梯度下降法:缓慢探索的徒步者
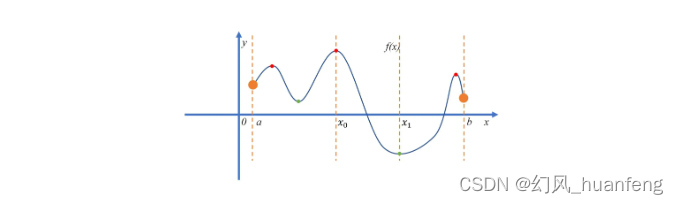
想象你是一位徒步者,站在一座多山的地形上,你的目标是到达最低点——山谷底部。你只能看到你周围有限的视野,看不到整个地形的全貌。为了决定往哪个方向走,你每走一步都会探测脚下的斜率,即地面倾斜的方向,然后沿着这个方向向下走一小步。这就是基础梯度下降法的工作原理,它按照当前位置的梯度(即损失函数下降最快的方向)逐步调整参数,以期达到最小损失值。
问题:如果地形中有许多小山包和凹陷(局部极小值),基础梯度下降可能会在这些局部低点附近徘徊,很难跳出并找到全局最低点。此外,在山谷较为平坦的区域,由于梯度变小,前进速度会大大减慢,可能导致收敛速度很慢。
(2)动量梯度下降法:带上滑板的探险者
现在,我们将徒步者换成了一个携带滑板的探险者,还是同样站在山顶,目标相同——到达山谷底部。除了根据当前的斜率决定滑行方向外,他还拥有一个特别的滑板,这个滑板能够累积之前的滑行速度。
当探险者开始下滑时,他的滑板不仅受到当前斜坡直接影响,还保留了前一次滑行的动量。这意味着,如果他在连续的斜坡上滑行,即使某个斜坡不如之前的陡峭,他也不会立刻慢下来,而是会凭借着积累起来的速度继续快速前进。相反,如果遇到反向的斜坡(相当于梯度方向的突然改变),滑板的动量也会帮助他更加平滑地调整方向,而不是立刻停下来或倒退。
二、通过定义来理性认识
动量梯度下降(Momentum Gradient Descent)算法是一种用于加速梯度下降算法收敛的方法,在数学上,它通过在梯度更新过程中引入“动量”来平滑序列变量更新,具体定义如下:
对于一个要优化的目标函数 ,其中
是参数向量,动量梯度下降算法在每次迭代
时对参数
进行更新,更新规则为:
在这个更新规则中:
是在时间步
的更新向量(可被认为是速度)它代表参数向量沿负梯度方向移动的大小和方向。
是动量因子(可称为摩擦系数)介于
区间,它衡量前一时间步更新向量
对当前更新的影响。较大的
值意味着前一步更新的影响更加持久,使得算法在参数空间内移动更加平滑。
是学习率,控制每一步沿梯度方向更新的大小。
-
是目标函数
关于参数向量
在
处的梯度,指示了目标函数下降最快的方向。
通过这种方式,动量项累积了过去的梯度信息,赋予了更新过程一种“惯性”,有助于算法在优化过程中更快地穿越平坦区域,减少振荡,并能更好地逃离局部极小值点。因此,动量梯度下降算法确实利用了指数加权平均的数学原理来改善了标准梯度下降的性能。
三、动量梯度下降法的优点
动量梯度下降法通过引入动量机制,提高了在非凸优化问题中寻找较好解的能力,并且通常能够更快且更稳定地收敛。具体来说有如下优点:
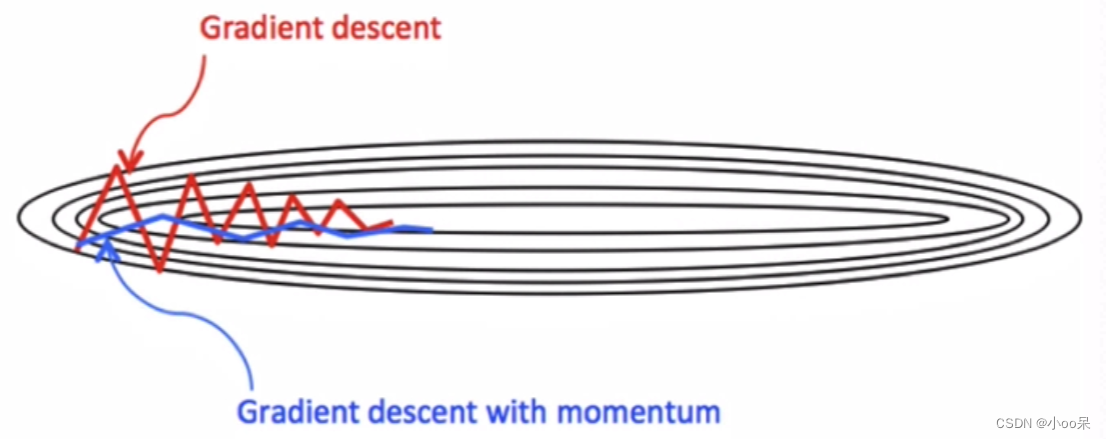
(1)减少振荡
在局部极小值附近,由于动量的作用,动量梯度下降能够减少在两侧的来回振荡,更容易跳出局部最优,寻找全局最优解。
(2)加快收敛
在接近最优解的平坦区域,即便梯度变小,动量项仍能提供一定的更新方向,维持一定的下降速度,加快收敛过程。
(3)克服局部极小值
在复杂的损失函数地形中,动量可以帮助算法更有效地穿越局部极小值(梯度接近零但不是极值点的地方),因为它结合了历史信息,不会轻易停止。