一、选题背景
近年来,人类大量燃烧煤炭、天然气等含碳燃料导致温室气 体过度排放,大量温室气体强烈吸收地面辐射中的红外线,造 成温室效应不断累积,使得地球温度上升,造成全球气候变暖。
气象温度的预测一直以来都是天气预测的重点问题,天气 不仅直接影响人们的健康、甚至影响人们的心情;此外,天气变 化还会影响一个国家的经济状况。....
二、方案论证(设计理念)
时间序列是按照统计将某一个事物的统计量发生的先后顺序的值按照统计时间排列的数列。时间序列分析通过已经发生的序列数值规律,来预测未来序列的数值情况,通常应用于连续序列的预测问题。例如:金融领域对下一个交易日大盘点数的预测;未来天气情况的预测;下一个时刻某种商品的销量情况的预测;电影票房变化情况的预测。简而言之,时间序列就是我们在不同时间点或者时间段上的对于某一种现象或行为观察得到的一组序列。
三、过程论述
数据来源为全球暖化数据集,在其中本文选取了中国主要城市天气状况表(月)该数据集,其中选择了北京市的数据情况,具体情况如下:
 首先进行数据的读取和相应的展示:
首先进行数据的读取和相应的展示:
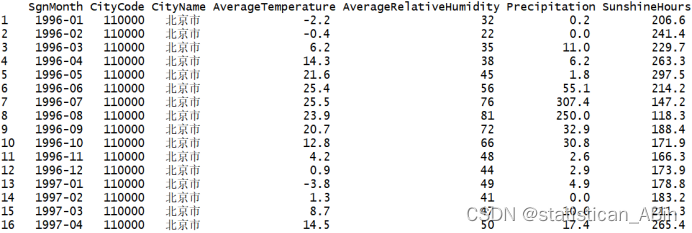
描述性统计分析

接下来进行数据的可视化展示:

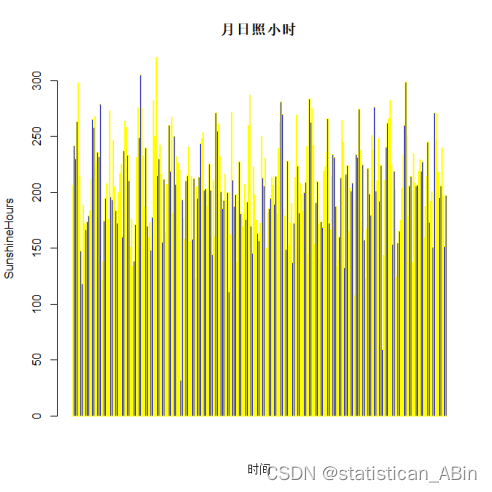
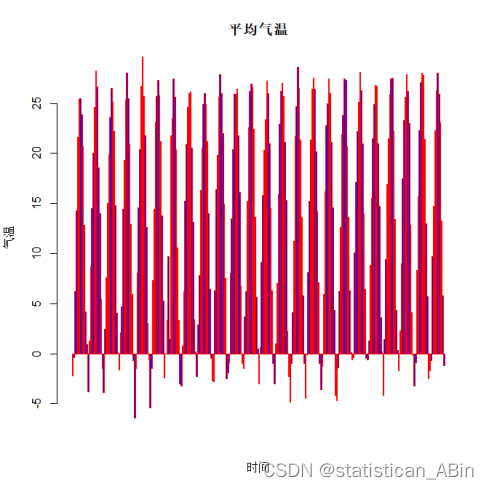
从上面四幅图可以看出,特别是最后一图,北京市1996-2019年的气温图,气温图有着极强的周期性、季节性。随后画出北京市1996-2019年的气温时序图。
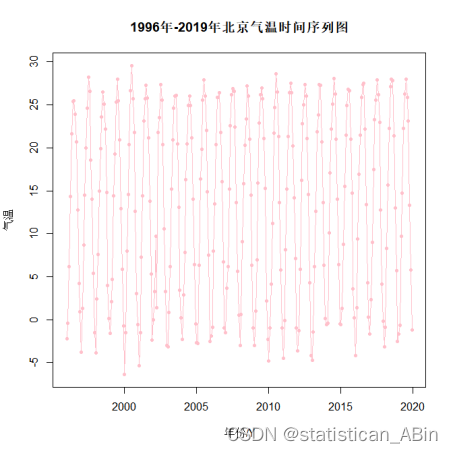
四、结果分析
进行模型构建前,要对序列数据纯随机性检验。可以判断数据是否具有建模的条件,如果没有,则没有意义建模。
表1 时间序列数据纯随机检验
| 滞后期数 | 卡方统计量 | P值 |
| 滞后6期P值 | 808.94 | 0.000 |
| 滞后12期P值 滞后18期P值 | 1216.9 2387.9 | 0.000 0.000 |
从上表结果可以看出,其p值均小于0.05,即在显著性水平为5%情况下,拒绝原假设,则可以进行建模
下面进行ADF检验,查看其平稳性,随后就进行模型自动定阶:
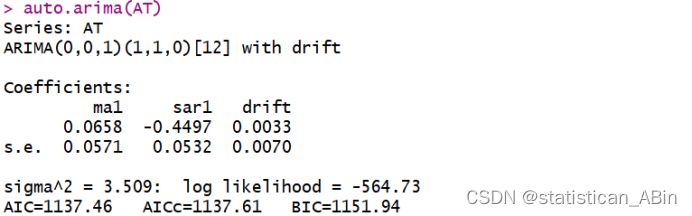

随后展示序列状态分布的qq图,情况如下:

模型预测
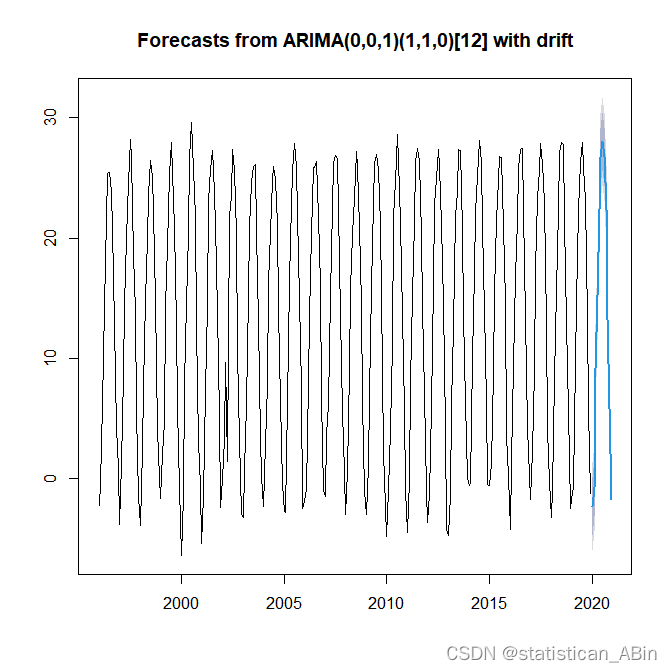
五、课程设计总结
在本研究中,选取了北京市1996-1至2019-12的数据进行研究,首先查看数据的具体情况,随后进行可视化,画出了其他变量的直方图,如气温、降水量、日照量等等,随后针对气温进行建模和分析,在建模前进行了一系列的检验,针对具有极强的季节性和周期性数据,本文最终的模型选择为ARIMA(0,0,1)(1,1,0)[12],最终预测了12其,即2020年全年的气温变化,直观的看,模型预测的较好,都较好的抓取了前面数据的特征,预测的结果也较符合客观规律。
代码:
library(openxlsx)
dataset<- read.xlsx("气温.xlsx", sheet = 1)
#View(dataset)
dataset
summary(dataset)#####描述性统计分析
###画出柱状图
###相对湿度
AverageRelativeHumidity<-dataset$AverageRelativeHumidity
AverageRelativeHumidity
barplot(AverageTemperature,xlab="时间",ylab="湿度",col="blue",main="平均相对湿度",border="blue")
###Precipitation降水量
Precipitation<-dataset$Precipitation
Precipitation
barplot(Precipitation,xlab="时间",ylab="Precipitation",col="blue",main="Precipitation降水量",border="green")
##月日照SunshineHours
SunshineHours<-dataset$SunshineHours
SunshineHours
barplot(SunshineHours,xlab="时间",ylab="SunshineHours",col="blue",main="月日照小时",border="yellow")
##平均气温
AverageTemperature<-dataset$AverageTemperature
AverageTemperature
barplot(AverageTemperature,xlab="时间",ylab="气温",col="blue",main="平均气温",border="red")###北京气温时间序列图
AverageTemperature
AT<-ts(AverageTemperature,start=c(1996),frequency=12)
AT
plot(AT,type="o",pch=20,main="1996年-2019年北京气温时间序列图",xlab = "年份/Y",ylab="气温",col = "pink")
#白噪声检验
for(i in 1:3) print(Box.test(AT,type = "Ljung-Box",lag=6*i))
###非白噪声,可建模###自动定阶
auto.arima(AT)
###模型拟合
AT.fit<-auto.arima(AT)
AT.fit
##模型评判选择
arima<-auto.arima(AT,trace=T)
accuracy(AT.fit)#模型预测
per_AT<-forecast(AT.fit,h=12)
per_AT
plot(per_AT)创作不易,希望大家多多点赞收藏和评论!