一:题目

二:原理讲解
解决这个题目 ,我们得先理解它的原理。
1:
首先假设两个指针,一个快指针fast,一个慢指针slow,fast一次移动两个节点,slow一次移动一个节点。(前面的直线代表进入环前面的节点,后面的圆圈就代表入环后的所有节点)
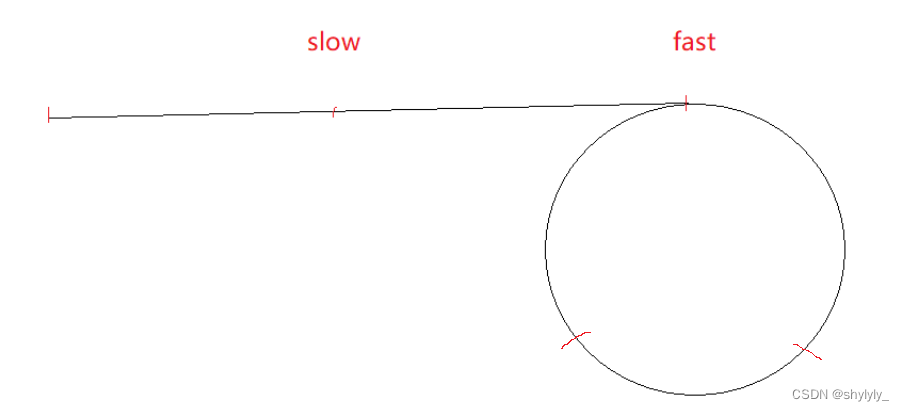
由博主前文环形链表(判断链表中是否有环)的讲解-CSDN博客可知,如果这是一个带环链表,那么二者fast和slow,最后会在环里相遇。
2:
二者相遇
第一种情况: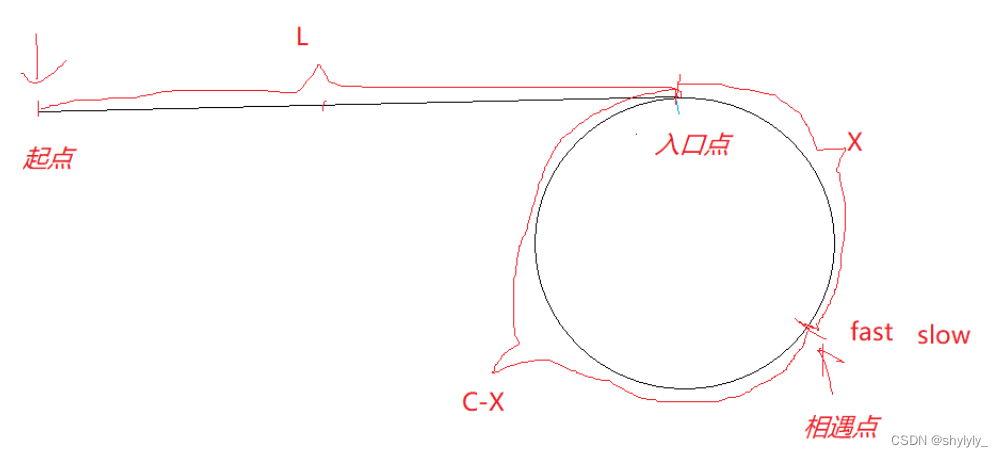
此时:我们假设起点到入口点的距离为L,环的周长为C,入口点到相遇点的距离为X。
因为:在截止相遇的那一刻,fast走的距离是slow的两倍。
由上图可知,slow走的距离为L+X,fast走的距离是L+C+X,
所以 2(L+X )= L+C+X,化简可得,L = C - X。
L = C - X是什么意思,意思就是,如果一个点从相遇点开始走(相遇点到入口点的距离是C-X),一个点从起点开始走(起点到入口点的距离是L),他们会在入口点相遇。
这个结论的意义是什么?
意义在于 :入口点就是我们题目要求的入环的第一个节点,而相遇点我们在前文中环形链表(判断链表中是否有环)的讲解-CSDN博客可以轻松得到。
但是这个分析是不完整的。
不完整的原因:
(因为还有第二种情况)
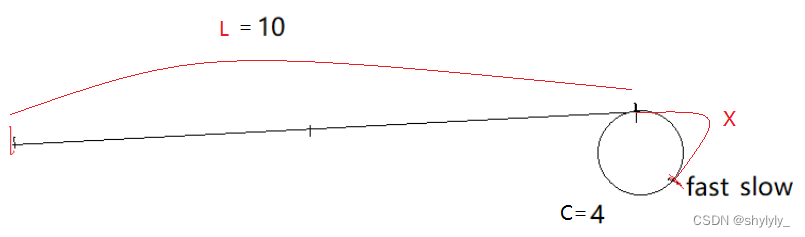
如果L = C - X,由图可知,当环比较小的时候,比如图中的C=4,进环前的节点很多的时候。
L = C - X,在这种情况下不会成立。
3:
完整的分析:
fast走的路程的确是slow 的两倍,但是fast不一定只是L+C+X,在第二种情况我们可以知道,fast应该在slow进入环之前,就已经可能在这个环内走了几圈。
所以正确的表达式应该是:2(L+X )= L+ n * C + X 。
n代表走的圈数:
由情况1可知,在slow进入环之前,fast在环内走的长度一圈都没有,在slow进入环后,fast开始追赶,最后走了一点距离,追上了slow,此时fast在slow进入环之前在环里走的距离+在slow进入环之后在环里追击所走的距离= 一圈,所以n的最低取值为1。(n≥1)
将2(L+X )= L+ n * C + X ,化简得到:L = C - X + (N-1) * C。
怎么理解 情况2 的结论:L = C - X + (N-1) * C 和 情况1: L = C - X 的区别?
情况1:如果一个指针a从相遇点开始走,一个指针b从起点开始走,他们会在入口点相遇。
情况2:如果一个指针a从相遇点开始走,一个指针b从起点开始走,他们会在入口点相遇。
看似两者一致,但是区别在于:
情况1:a指针从相遇点开始走到和b指针在入口点相遇的时候,a指针在环内只走了 C - X,一圈不到的长度。
情况2:a指针从相遇点开始走到和b指针在入口点相遇的时候,a指针在环内走了 C - X + (N-1) * C ,走了N-1圈 ,然后再走了C - X 的长度。
代码展示:

结论:当我们通过快慢指针得到相遇节点,一个指针从相遇节点开始走,一个指针从起点开始走,二者会在环的入口节点相遇。

![[单片机课设]十字路口交通灯的设计](https://img-blog.csdnimg.cn/direct/d1f68f1c2e1f4a758454b54511f9163f.png)