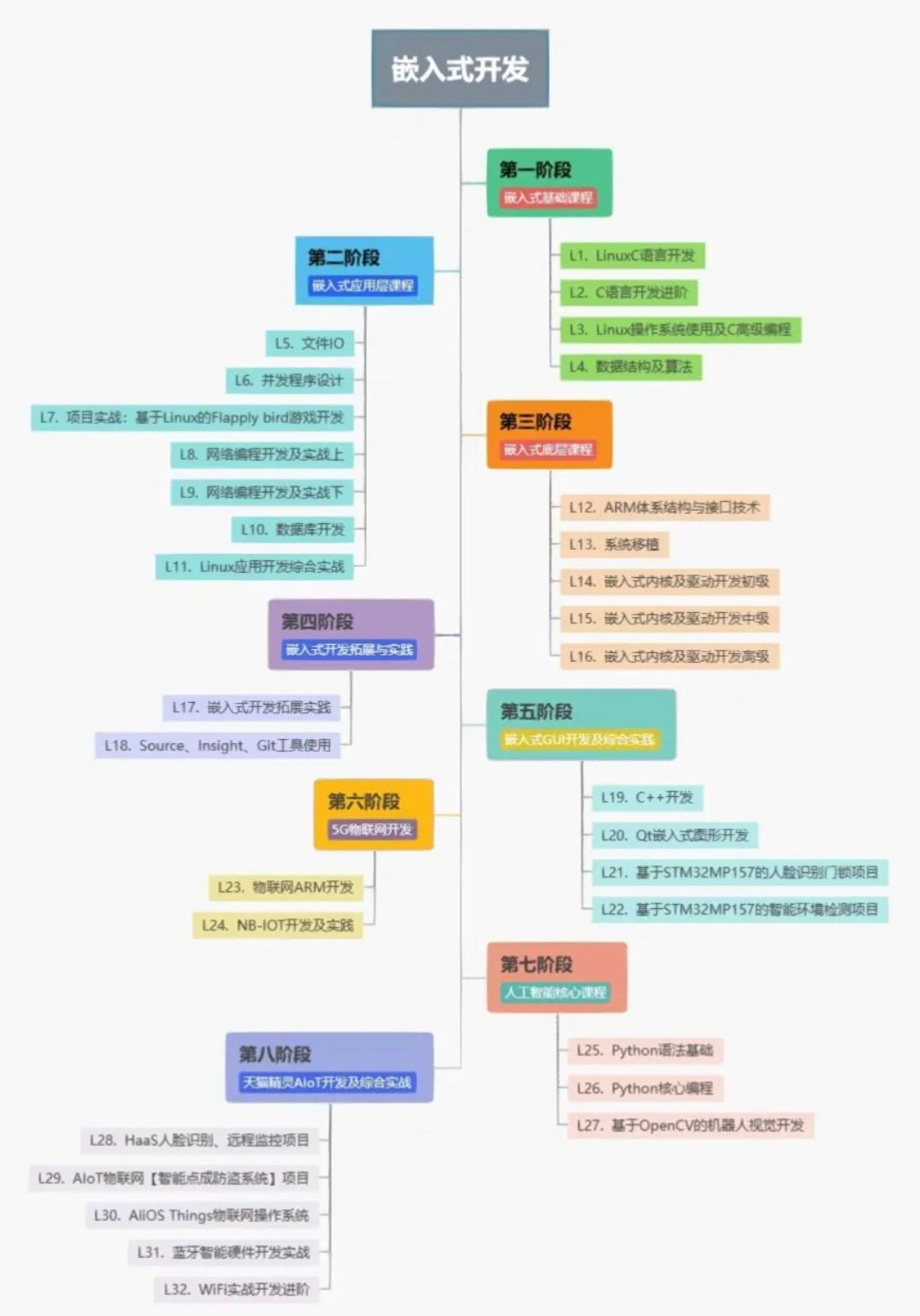
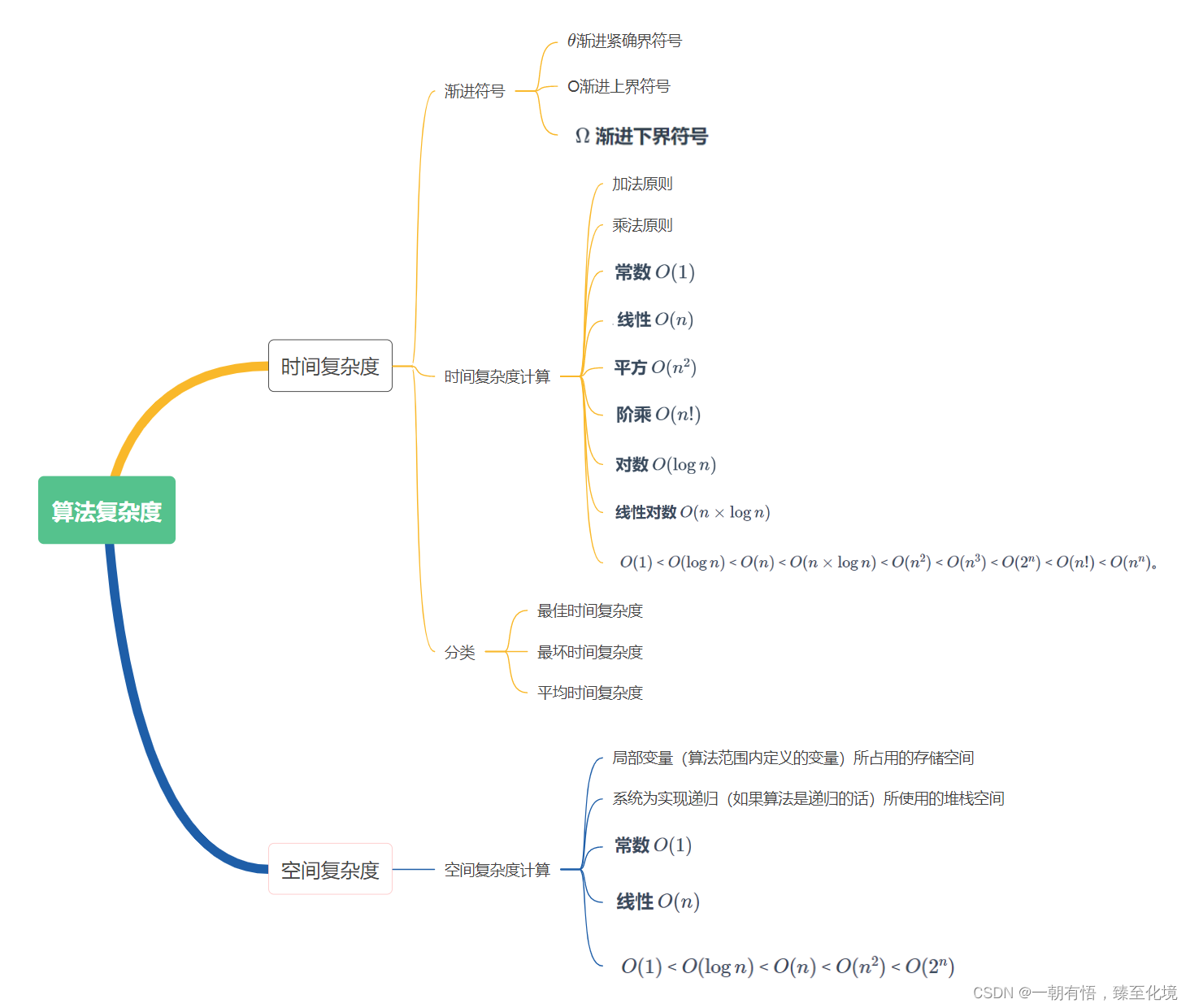
对于时间复杂度，主要包括三种情况：

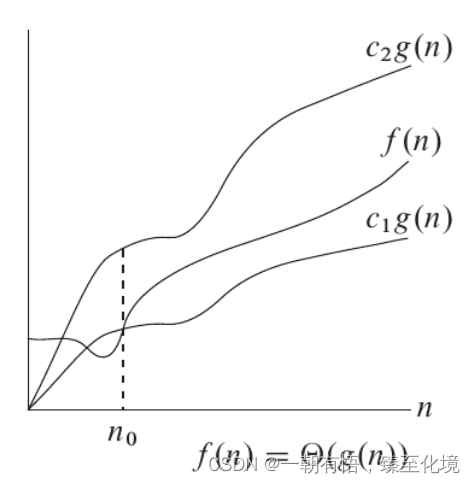
渐进紧确界：

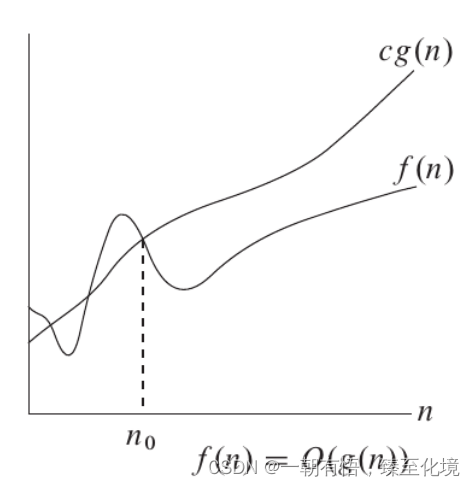
O渐进上界：

渐进下界：

加法原则：不同的时间复杂度相加取阶数最高的

乘法原则：不同的时间复杂度相乘，结果为时间复杂度的乘积 

阶乘时间复杂度一般出现在全排列和旅行商问题中，而对数时间复杂度一般出现在分治算法中。

对于平均时间复杂度举例

def find(nums, val):pos = -1for i in range(n):if nums[i] == val:pos = ibreakreturn pos

在这个代码中，最好时间复杂度为O(1)，最坏时间复杂度为O(n)。这样时间复杂度就不唯一，所以此时我们需要计算平均时间复杂度。对于这个算法总共有n+1种情况，即在n个位置上找到指定元素和最终没有找到指定元素。对其求平均即可得，所以平均时间复杂度就为O(n)。

空间时间复杂度的计算就较为简单，主要包括局部变量所占用的存储空间和进行递归时所使用的堆栈空间。 一般将算法的辅助空间作为评判算法空间复杂度大小的标准。