前言

本篇旨在介绍使用向上调整建堆与向下调整建堆的时间复杂度. 以及topk问题

博客主页: 酷酷学!!!
感谢关注~

建堆的时间复杂度

堆排序是一种优于冒泡排序的算法, 那么在进行堆排序之前, 我们需要先创建堆, 为什么说堆排序的是优于冒泡排序的呢? 那么这个建堆的时间复杂度是多少呢?

void HeapSort(int* a, int n)
{//降序//创建小堆//向下调整创建,从最有一个非叶子节点//时间复杂度O(N)for (int i = (n-1-1)/2; i>=0; i--){Adjustdown(a, n, i);}//堆创建之后,交换第一个节点与最后一个节点,//时间复杂度为O(N*logN)int end = n-1;while (end > 0){Swap(&a[0], &a[end]);Adjustdown(a, end, 0);end--;}
}

首先来看向下调整算法建堆的时间复杂度, 因为堆是完全二叉树，而满二叉树也是完全二叉树，此处为了简化使用满二叉树来证明(时间复杂度本来看的就是近似值，多几个结点不影响最终结果)：

假设高度为h的二叉树, 结点的个数为N, 可以计算出高度h与结点个数之间的关系如下图所示:

向下调整算法, 从最后一个非叶子结点开始向下调整, 也就是第h-1层, 需要向下移动一层, 第h-2层需要向下移动2层, … , 第一层则需要向下移动h-1层, 第二层的结点需要向下移动h-2层. 依次类推, 如图所示.

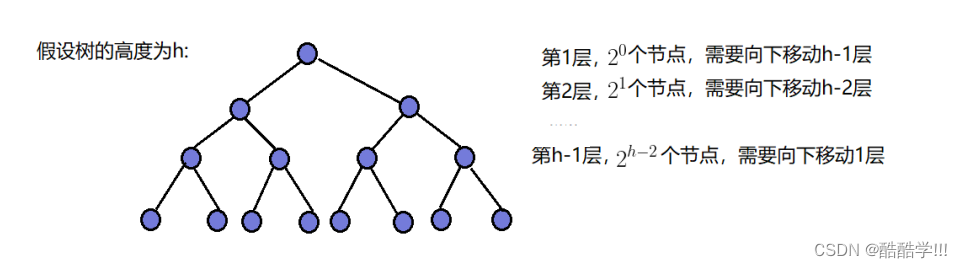
可以看出节点数量多的层调整次数少, 结点数量少的层调整次数多 . 错位相减法则可以计算出T(N) = 2^h - 1 - h, 带入h与N的关系则得出向下调整建堆的时间复杂度为O(N).

void Heapsort(int* a,int n)
{//时间复杂度为O(N*logN)for (int i = 1; i < n; i++){AdjustUP(a, i);}//时间复杂度为O(N*logN)int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);end--;}
}

使用向上调整建堆, 计算其时间复杂度, 如下

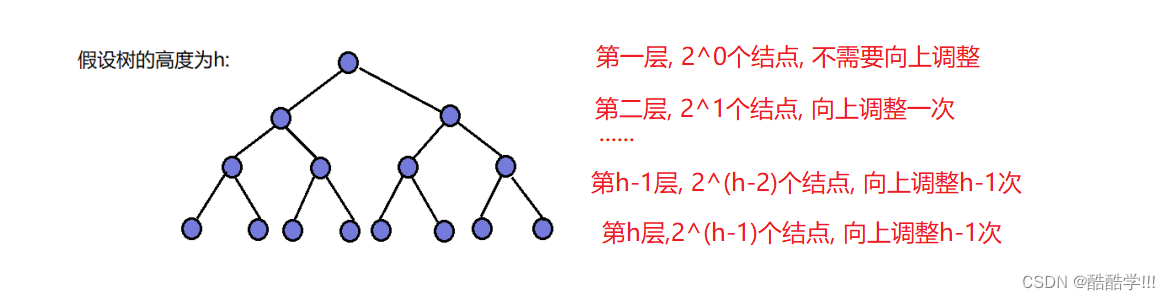
总计调整次数为

使用错位相减法计算:

可以看出结点数多的层, 调整次数也多, 结点数少的层, 调整次数少, 时间复杂度为O(N*logN), 所以一般建堆都采用向下调整建堆法.

TOPK问题

TOP-K问题：即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。
比如：专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
对于Top-K问题，能想到的最简单直接的方式就是排序，但是：如果数据量非常大，排序就不太可取了(可能数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决，基本思路如下：

1. 用数据集合中前K个元素来建堆

前k个最大的元素，则建小堆
前k个最小的元素，则建大堆

2. 用剩余的N-K个元素依次与堆顶元素来比较，不满足则替换堆顶元素

将剩余N-K个元素依次与堆顶元素比完之后，堆中剩余的K个元素就是所求的前K个最小或者最大的元素。

例如: 求十万个数据中最大的前K个数, 要求只有1kb内存, 这些数据存储在磁盘中

首先先用前k个数建一个小堆, 剩下的N-K个元素依次与堆顶元素进行比较, 如果大于堆顶元素, 则替换堆顶元素, 并且向下调整堆, 结束后, 堆中数据即最大的k个元素.

代码如下:

第一步先使用随机数生成十万个数据

void CreateNDate()
{// 造数据int n = 100000;srand(time(0));const char* file = "data.txt";FILE* fin = fopen(file, "w");if (fin == NULL){perror("fopen error");return;}for (int i = 0; i < n; ++i){int x = (rand()+i) % 10000000;fprintf(fin, "%d\n", x);}fclose(fin);
}

读取数据, 并且用前k个数据创建一个小堆, 然后读取剩下的数据, 如果比堆顶数据大, 就替代堆顶数据进入堆, 然后向下调整堆.

void TestHeap()
{int k;printf("请输入k>:");scanf("%d", &k);int* kminheap = (int*)malloc(sizeof(int) * k);if (kminheap == NULL){perror("malloc fail");return;}const char* file = "data.txt";FILE* fout = fopen(file, "r");if (fout == NULL){perror("fopen error");return;}// 读取文件中前k个数for (int i = 0; i < k; i++){fscanf(fout, "%d", &kminheap[i]);}// 建K个数的小堆for (int i = (k-1-1)/2; i>=0 ; i--){AdjustDown(kminheap, k, i);}// 读取剩下的N-K个数int x = 0;while (fscanf(fout, "%d", &x) > 0){if (x > kminheap[0]){kminheap[0] = x;AdjustDown(kminheap, k, 0);}}printf("最大前%d个数：", k);for (int i = 0; i < k; i++){printf("%d ", kminheap[i]);}printf("\n");
}

int main()
{CreateNDate();TestHeap();return 0;
}

总结

建堆的时间复杂度为O(N), 使用堆排序的时间复杂度为O(N*logN), 而使用冒泡排序的时间复杂度为O(N^2), 故堆排序的效率明显高于冒泡排序, 而topk则解决了使用较小内存而求取一堆数据中最大或者最小的前k个数据.