数据测试简介

  简而言之，数据测试就是对数据的质量进行测试，查看该质量能不能被我方接受。在风控中，数据测试的主要目的是测试对方数据源是否可以较好地区分出我方申请用户的好坏，衡量质量的指标主要包括：Lift-Chart、AUC、KS、WOE、IV。
注：下面所有的解释均是从风控角度出发

Lift Chart

  Lift Chart被广泛的应用于风控阈值选择中，用来衡量某个风险分对好坏人的单调程度和区分度，它一般以两种形态出现：normal、accumulative。

• normal：直观地衡量被测试风险分数的单调性
• accumulative：有助于快速选择风险分数的阈值
  

  上图中坏人占比就是nromal，即每段样本中坏人的占比。而坏人累积占比则是accumulative，即每段样本中坏人累积占比，计算方法是“前n段坏人总数 / 前n段样本总数”。橙色的线单调递增，说明该风险分数是分数越高风险越大，整体可以看出该风险分数很稳定，绿色的线的最后一个点代表整体的坏账率为8.8%。

• 假设我方可接受的坏账风险是7%且我方承担坏账风险，那么一般情况下，会根据橙色的线去选择风险分阈值，结合图发现第6段风险分对应的坏账率为6.7%（略低于7%），所以可以再对6、7段样本进行细分从而找到7%对应的具体风险分数作为阈值，此时该分数的通过率在6%多一点
• 当是对方承担风险的时候，会根据绿色的线去选择风险分阈值，结合图发现第9段风险分对应的累积坏账率为6.9%（略低于7%），那么就可以直接用9分作为风险分阈值，此时该分数的通过率为90%

注：若每段的样本量不多（300左右），一般情况下橙色的线会出现较大的波动，这时就需要结合一定的经验进行选择阈值。

WOE

  WOE(Weight of Evidence)，衡量的是每个风险分段中坏样本与好样本的比值，和整体样本中坏样本与好样本比值的差异。WOE的取值范围是[-∞, +∞]，其绝对值越大，这种差异越大，即该风险分数段中的坏样本占比更大。
$$WO{E}_i=ln(\frac{p{y}_i}{p{n}_i})=ln(\frac{y_i/y_T}{n_i/n_T})=ln(\frac{y_i/n_i}{y_T/n_T})$$

• $p{y}_i$：第$i$段样本中坏样本占坏样本总数的比例
• $p{n}_i$：第$i$段样本中好样本占好样本总数的比例
• $y_i$：第$i$段样本中坏样本的个数
• $n_i$：第$i$段样本中好样本的个数
• $y_T$：坏样本的总个数
• $n_T$：好样本的总个数

IV

  IV(Information Value)，衡量风险分数对区分好坏人的价值，IV值的取值范围是[0, +∞)，取值越大说明该风险分数的价值越高。
$$IV=\sum _{i=1}^{|I|}I{V}_i=\sum _{i=1}^{|I|}(p{y}_i-p{n}_i)\ast WO{E}_i=\sum _{i=1}^{|I|}(p{y}_i-p{n}_i)\ast ln(\frac{y_i/n_i}{y_T/n_T})$$

• $|I|$：风险分数被分的段数

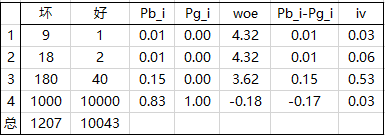
  显而易见，IV是对WOE的加权求和，其巧妙之处就是这个权重$p{y}_i-p{n}_i$。其巧妙之处如下：
  为了避免最后风险分数的价值出现负数的情况，即${\sum }_{i=1}^{|I|}WO{E}_i$不为负，那么必须对$WO{E}_i$进行一定的变换。第一个想到的是取绝对值，但是这种方法不可取，主要是因为单纯的取绝对值并不能避免每段样本量分布不均且某个（些）坏样本占比很大时对IV值的影响：

ROC

  ROC曲线用来评价模型的好坏，它的横轴是FPR（假正例率），纵轴是TPR（真正例率）。FPR衡量的是“从好样本中挑出了多少比例的好样本作为坏样本”，TPR衡量的是“从坏样本中挑出了多少比例的坏样本作为坏样本”。

AUC

  AUC是ROC曲线下的面积，AUC衡量的是模型分数的排序性。从另一个角度来讲，AUC指的是：当你随机抽取一个好样本和一个坏样本，好样本的分数大于坏样本分数的概率。AUC的取值范围是[0, 1]，AUC越大，排序性越好。

KS

  KS是ROC的另一种可视化形式，将TPR和FPR都放到了纵轴上面。