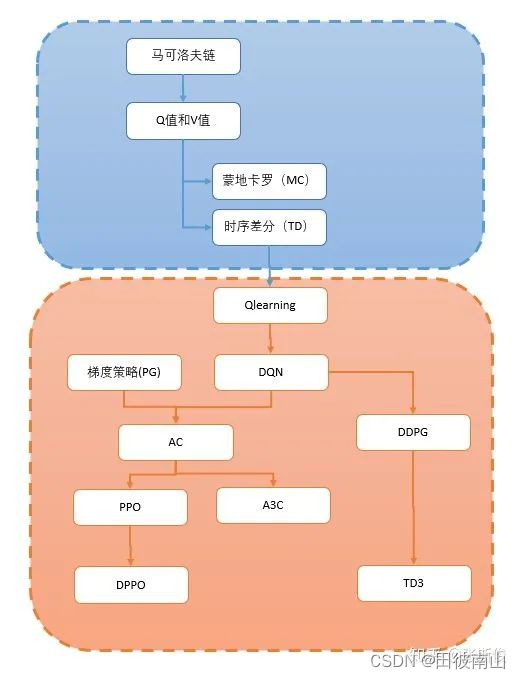
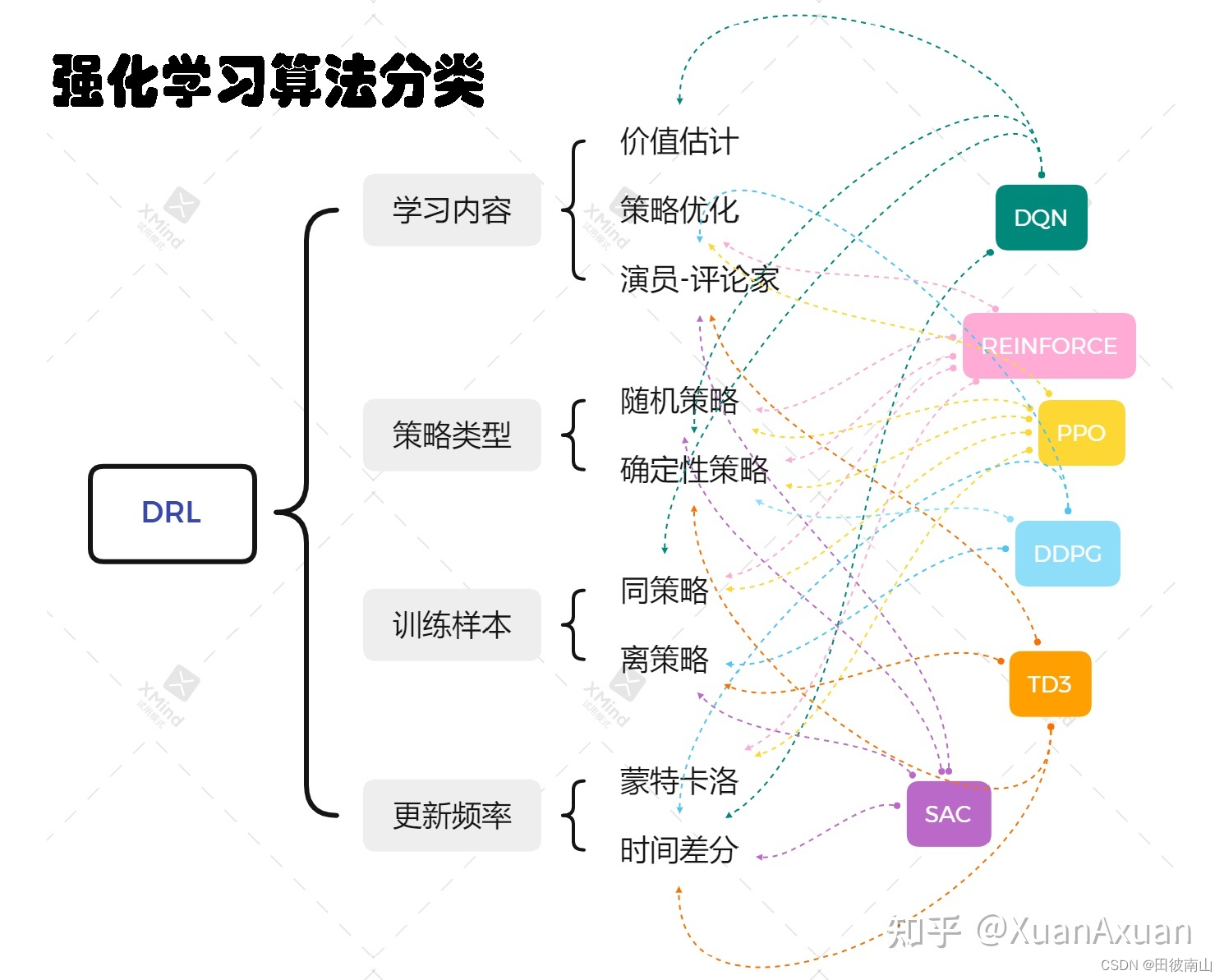
- 从上图看出,强化学习可以分成价值/策略、随机策略/确定策略、在线策略/离线策略、蒙特卡洛/时间差分这四个维度。这里分析了基础算法中除了在线策略/离线策略以外的其他维度。
(一)基础知识
一、基础概念
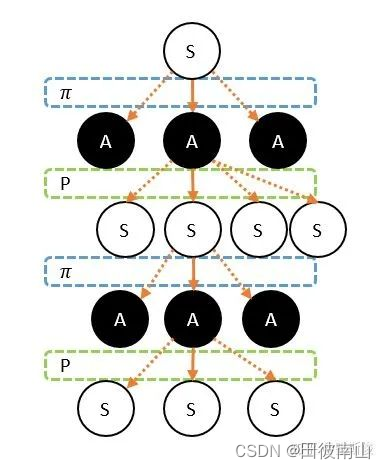
- 重点概念:状态S、动作A、策略 π \pi π、奖励r、折扣率 γ \gamma γ、回报G、转移概率P、状态价值V(s)、状态-动作价值Q(s,a)
- (状态、动作、策略、奖励、折扣率)是马尔科夫过程的五元组
- 所谓的模型实际是给出了转移概率和奖励值
- 奖励是在离开当前“情况”时获得的,这里说的“情况”包括“状态”和“动作”。因为顺序是sarsa,所以r是在动作后给出的,是一个步骤中最后给出的。
- 回报是未来长期奖励的累计。这里有一个点需要注意,这个回报可以从任意节点开始,这里的节点可以指状态也可以指动作,分别对应状态价值和状态动作价值
回报的定义
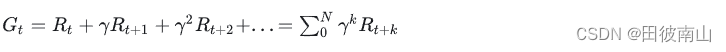
- 价值函数都是回报的期望
状态价值的定义

状态-动作价值的定义
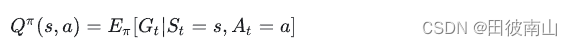
二、贝尔曼期望公式(V和Q的关系)
https://zhuanlan.zhihu.com/p/110338833
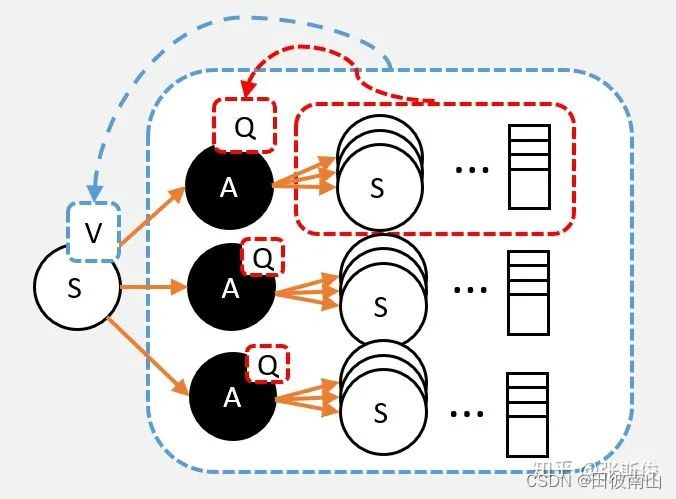
1、用Q表示V
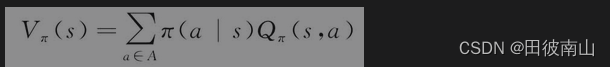
- Q的期望是V
2、用V表示Q
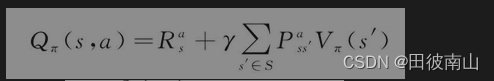
3、用下一个V表示当前的V(V迭代)
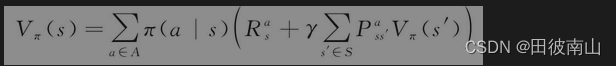
- 2带入1得到3
4、用下一个Q表示当前的Q(Q迭代)
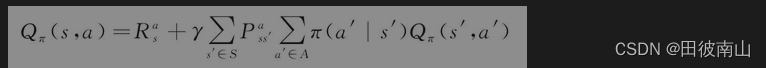
- 1带入2得到4
三、MC与TD
- 这两种算法不是应用在某一种强化学习算法上,而是广泛的存在强化学习中,所有的算法几乎都可以利用这两种思路分成两类。在基础算法的学习中,是仅次于基于值和策略以外最应当关注的分类。
1、MC:使用采样的方法,利用平均值进行估计
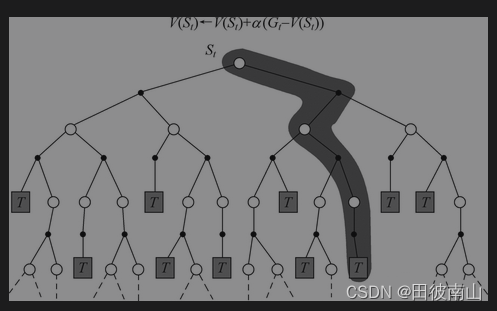
2、TD:多采一步数据,利用下一次的计算值进行估计
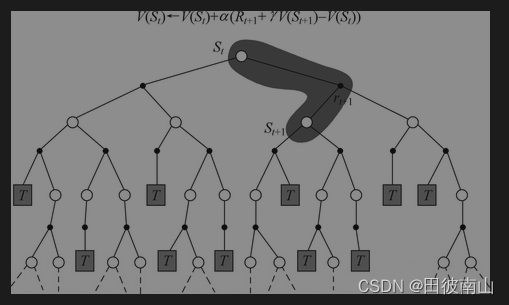
(二)基于值的强化学习
一、V更新
1、更新公式
V n e w ( s ) = V o l d ( s ) + α [ V r e a l ( s ) − V o l d ( s ) ] V_{new}(s)=V_{old}(s)+\alpha[V_{real}(s)-V_{old}(s)] Vnew(s)=Vold(s)+α[Vreal(s)−Vold(s)]
-
上式是V更新过程的理想公式,真实价值函数值与过去价值函数值的差就是应当更新价值函数的方向
V n e w ( s ) = V o l d ( s ) + α [ V e s t i m a t e ( s ) − V o l d ( s ) ] V_{new}(s)=V_{old}(s)+\alpha[V_{estimate}(s)-V_{old}(s)] Vnew(s)=Vold(s)+α[Vestimate(s)−Vold(s)] -
但是我们实际上并没有真实价值函数(要不然干嘛还要更新这个价值函数呢),所以只能用不同的方法去估计这个真实价值函数值,也就是上式。采用不同的估计方法就产生了不同的基于值的强化学习算法
-
后续Q的更新公式是一样的,思路都是一样的
2、MC
V e s t i m a t e ( s ) = G = G 1 + G 2 + … … + G n N V_{estimate}(s)=G=\frac{G_1+G_2+……+G_n}{N} Vestimate(s)=G=NG1+G2+……+Gn
V n e w ( s ) = V o l d ( s ) + α [ G − V o l d ( s ) ] V_{new}(s)=V_{old}(s)+\alpha[G-V_{old}(s)] Vnew(s)=Vold(s)+α[G−Vold(s)]
- 用采样的G估计V的真实值
3、TD(TD(0))
V e s t i m a t e ( s ) = γ V o l d ( s ′ ) + r ′ V_{estimate}(s)={\gamma}V_{old}(s')+r' Vestimate(s)=γVold(s′)+r′
V n e w ( s ) = V o l d ( s ) + α [ γ V o l d ( s ′ ) + r ′ − V o l d ( s ) ] V_{new}(s)=V_{old}(s)+\alpha[{\gamma}V_{old}(s')+r'-V_{old}(s)] Vnew(s)=Vold(s)+α[γVold(s′)+r′−Vold(s)]
- 用下一个状态的V估计现在的V真值
- 注意这里有一个特别的点,由S状态出发,S’有不同的可能状态,这里是使用了在这一次实验中策略函数实际给出的状态S‘。也就是对应着Q更新中的SARSA
二、Q更新
1、更新公式
Q n e w ( s ) = Q o l d ( s ) + α [ Q r e a l ( s ) − Q o l d ( s ) ] Q_{new}(s)=Q_{old}(s)+\alpha[Q_{real}(s)-Q_{old}(s)] Qnew(s)=Qold(s)+α[Qreal(s)−Qold(s)]
Q n e w ( s ) = Q o l d ( s ) + α [ Q e s t i m a t e ( s ) − Q o l d ( s ) ] Q_{new}(s)=Q_{old}(s)+\alpha[Q_{estimate}(s)-Q_{old}(s)] Qnew(s)=Qold(s)+α[Qestimate(s)−Qold(s)]
2、MC
Q e s t i m a t e ( s ) = G = G 1 + G 2 + … … + G n N Q_{estimate}(s)=G=\frac{G_1+G_2+……+G_n}{N} Qestimate(s)=G=NG1+G2+……+Gn
Q n e w ( s ) = Q o l d ( s ) + α [ G − Q o l d ( s ) ] Q_{new}(s)=Q_{old}(s)+\alpha[G-Q_{old}(s)] Qnew(s)=Qold(s)+α[G−Qold(s)]
- 用采样的G估计Q的真实值
- 用于估计V和Q的G,是针对不同情况(s或者(s,a))的G
3、TD
https://zhuanlan.zhihu.com/p/110338833
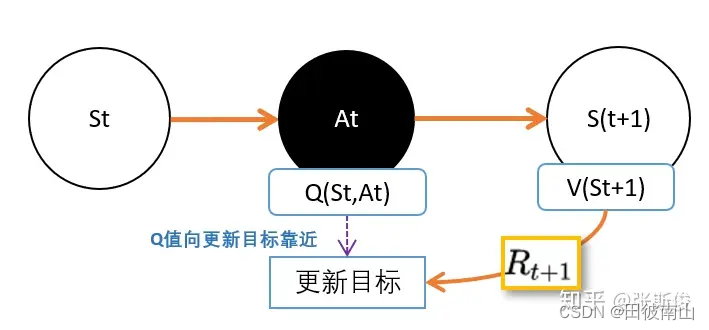
Q e s t i m a t e ( s ) = γ V o l d ( s ′ ) + r ′ Q_{estimate}(s)={\gamma}V_{old}(s')+r' Qestimate(s)=γVold(s′)+r′
Q e s t i m a t e ( s ) = γ ∑ a ∈ A π ( a ∣ s ′ ) Q π ( s ′ , a ) + r ′ Q_{estimate}(s)={\gamma}{\sum_{a\in A} \pi(a|s')Q_{\pi}(s',a)}+r' Qestimate(s)=γa∈A∑π(a∣s′)Qπ(s′,a)+r′
- 上面是完整的估计方法,但是计算量太大,反正都是估计了,旧的Q本来就不准。思路是用一个特别的Q代替V,使得Q一定程度上可以代替V,SARSA是使用旧策略输出动作的Q,Q-learning是选择Q最大的动作计算Q。
(1)SARSA
Q e s t i m a t e ( s ) ∝ [ γ Q π ( s ′ , π ( a ∣ s ′ ) ) + r ′ ] Q_{estimate}(s) \propto [{\gamma}{ Q_{\pi}(s',\pi(a|s'))}+r'] Qestimate(s)∝[γQπ(s′,π(a∣s′))+r′]
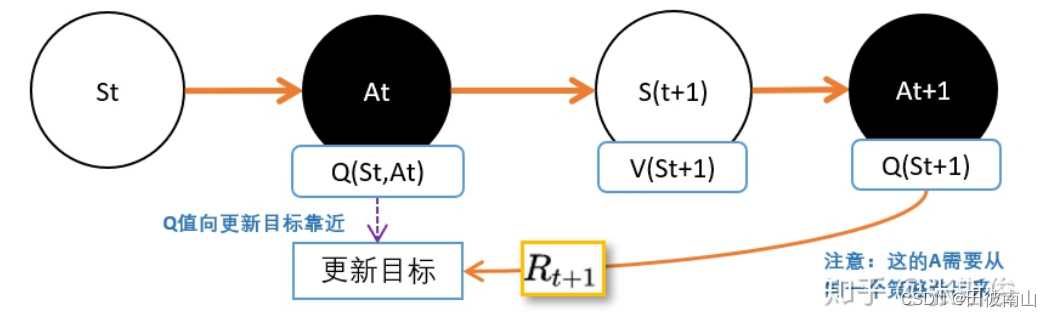
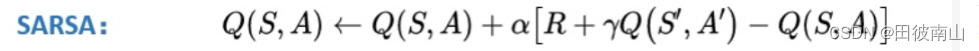
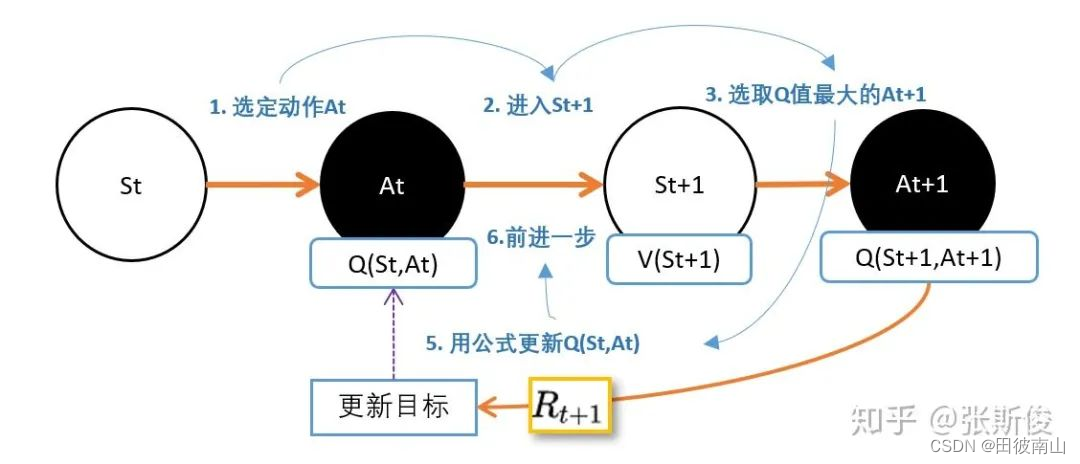
(2)Q-learning
Q e s t i m a t e ( s ) ∝ [ γ m a x a ∈ A ( Q π ( s ′ , π ( a ∣ s ′ ) ) ) + r ′ ] Q_{estimate}(s) \propto [{\gamma}{ max_{a\in A}(Q_{\pi}(s',\pi(a|s')))}+r'] Qestimate(s)∝[γmaxa∈A(Qπ(s′,π(a∣s′)))+r′]
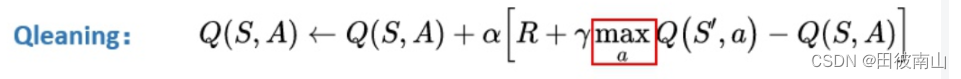
(3)DQN=Qlearning+NN
Q e s t i m a t e ( s ) = f n n ( s ) Q_{estimate}(s)=f_{nn}(s) Qestimate(s)=fnn(s)
损失函数 L o s s = Q e s t i m a t e ( s ) − Q o l d ( s ) = f n n ( s ) − Q o l d ( s ) 损失函数Loss=Q_{estimate}(s) - Q_{old}(s) = f_{nn}(s) - Q_{old}(s) 损失函数Loss=Qestimate(s)−Qold(s)=fnn(s)−Qold(s)
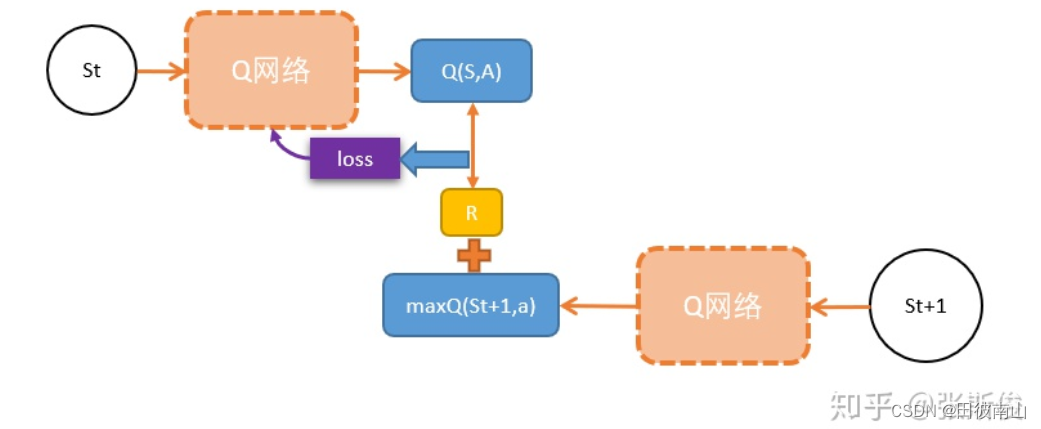
- 这里涉及到了损失函数的部分,虽然时间差分是用下一步估计这一步但是都是用的同一个Q函数,凭什么说下一步估计的更准呢?个人认为这里的思路是带奖励R的估计值会比原来的计算值更准,因为R是客观的,不断的迭代才导致最终收敛。
(三)基于策略的强化学习
- 策略梯度的应用空间更广,不仅适用于确定、离散的问题,也适用于随机、连续的问题。
- 策略梯度分为随机策略梯度和确定策略梯度,这一部分都是随机策略梯度的
一、更新公式(策略梯度)
https://www.zhihu.com/question/556911056/answer/3378158668
https://zhuanlan.zhihu.com/p/137416242
https://zhuanlan.zhihu.com/p/70260658
https://blog.csdn.net/weixin_40493501/article/details/110671785?spm=1001.2014.3001.5502
1、梯度上升最大化目标函数J
θ t + 1 = θ t + α ∇ J ( θ ) \theta_{t+1} = \theta_{t} + \alpha\nabla{J(\theta)} θt+1=θt+α∇J(θ)
- 梯度比较常用的做法是用梯度下降最小化损失函数。其实如果理解梯度的概念的话,就能明白不一定是损失函数,也不一定是最小化。
2、策略梯度定理推导
∇ J ( θ ) = E π [ ∇ l o g ( π θ ( s , a ) ) ∗ Q π ( s , a ) ] \nabla{J(\theta)}=E_{\pi}[\nabla{log(\pi_{\theta}(s,a))}*Q_{\pi}(s,a)] ∇J(θ)=Eπ[∇log(πθ(s,a))∗Qπ(s,a)]
- 问题的关键就来到了如何计算目标函数关于控制策略参数的梯度
- 这里的目标函数定义为状态价值函数V



3、从物理角度的理解
∇ J ( θ ) = E π [ ∇ l o g ( π θ ( s , a ) ) ∗ Q π ( s , a ) ] \nabla{J(\theta)}=E_{\pi}[\nabla{log(\pi_{\theta}(s,a))}*Q_{\pi}(s,a)] ∇J(θ)=Eπ[∇log(πθ(s,a))∗Qπ(s,a)]
- 上面这个公式是策略梯度定理,可以理解为“带权重的梯度”
- ∇ l o g ( π θ ( s , a ) ) \nabla{log(\pi_{\theta}(s,a))} ∇log(πθ(s,a))基本可以等价于策略关于 θ \theta θ的梯度方向,是“策略的梯度”。就像y=ax+b中的x和1,代表着改进的方向,也就是说从这个方向改变参数可以尽量快的增大或者减小后面部分的效果。要区分这里的“带权重梯度”和后续DDPG中“目标函数梯度”。
- Q π ( s , a ) Q_{\pi}(s,a) Qπ(s,a)代表着环境反馈的好与坏,如果长期奖励大于0代表好行为则沿着梯度加大,如果长期奖励小于0代表坏行为则沿着梯度减小
- 对于这个公式不同处理和估计方式,衍生出了不同基于策略的强化学习方法,就像下面这张图中给出的:

二、基于蒙特卡洛的策略梯度(REINFORCE)
∇ J ( θ ) = E π [ ∇ l o g ( π θ ( s , a ) ) ∗ Q π ( s , a ) ] \nabla{J(\theta)}=E_{\pi}[\nabla{log(\pi_{\theta}(s,a))}*Q_{\pi}(s,a)] ∇J(θ)=Eπ[∇log(πθ(s,a))∗Qπ(s,a)]
∇ J ( θ ) = ∇ l o g ( π θ ( s , a ) ) ∗ G t \nabla{J(\theta)}=\nabla{log(\pi_{\theta}(s,a))}*G_t ∇J(θ)=∇log(πθ(s,a))∗Gt
θ t + 1 = θ t + α ( ∇ l o g ( π θ ( s , a ) ) ∗ G t ) \theta_{t+1} = \theta_{t} + \alpha(\nabla{log(\pi_{\theta}(s,a))}*G_t) θt+1=θt+α(∇log(πθ(s,a))∗Gt)
- 蒙特卡洛方法就是把期望用多次采样的平均数进行估计
- 注意这里实际上做了两次蒙特卡洛,只是第二次除了去除E以外没啥作用,推导过程如下

三、基于时间差分的策略梯度
1、(演员评论家AC)
https://zhuanlan.zhihu.com/p/110998399
基于蒙特卡洛的策略梯度: θ t + 1 = θ t + α ( ∇ l o g ( π θ ( s , a ) ) ∗ G t ) \theta_{t+1} = \theta_{t} + \alpha(\nabla{log(\pi_{\theta}(s,a))}*G_t) θt+1=θt+α(∇log(πθ(s,a))∗Gt)
带基线的蒙特卡洛策略梯度: θ t + 1 = θ t + α ( ∇ l o g ( π θ ( s , a ) ) ∗ ( G t − b ) ) \theta_{t+1} = \theta_{t} + \alpha(\nabla{log(\pi_{\theta}(s,a))}*(G_t-b)) θt+1=θt+α(∇log(πθ(s,a))∗(Gt−b))
演员评论家: θ t + 1 = θ t + α ( ∇ l o g ( π θ ( s , a ) ) ∗ ( Q π ( s , a ) − V π ( s , a ) ) ) \theta_{t+1} = \theta_{t} + \alpha(\nabla{log(\pi_{\theta}(s,a))}*(Q_{\pi}(s,a)-V_{\pi}(s,a))) θt+1=θt+α(∇log(πθ(s,a))∗(Qπ(s,a)−Vπ(s,a)))
- 演员加评论者中的G不用蒙特卡洛算法就还是Q,而用Q的平均值作为基线b。Q的平均值就等于V,并定义Q-V为TD-error,可以参考下图
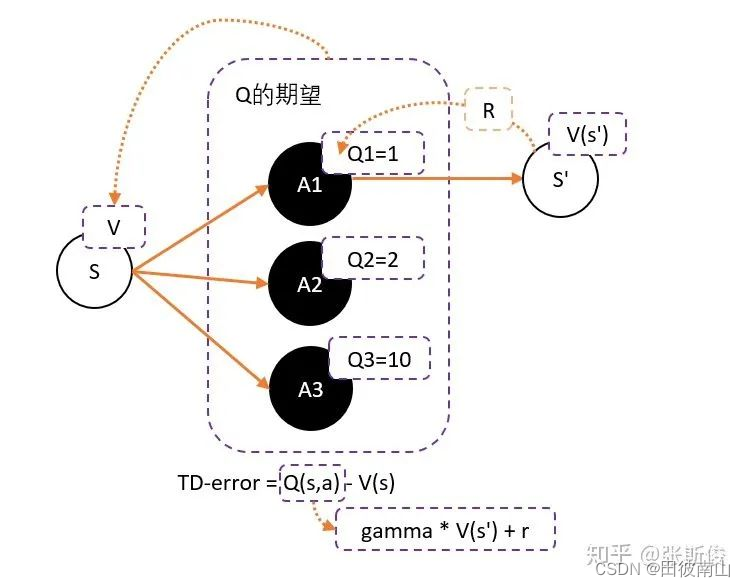
演员评论家的架构如下所示
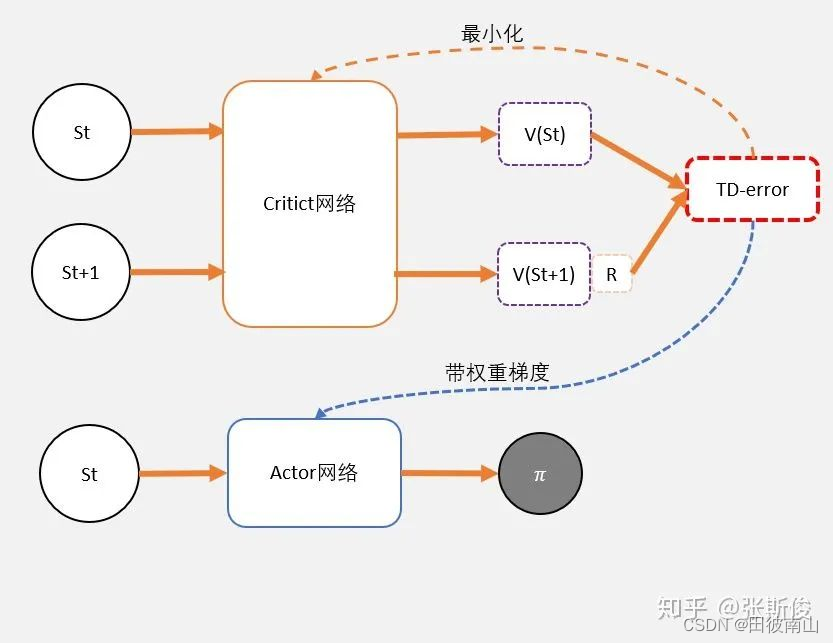
- 评论者输入状态St输出状态价值V(St),TD-error可以作为评论者的loss。这里采用了TD的思想,也就是用下一步的V估计这一步的V,认为有客观的奖励参与的估计值比单独计算的准,所以跟一般的固定标签的神经网络不同。
- 演员则把TD-error作为“权重梯度”中的“权重”
(四)结合策略和值的强化学习算法
资料:
DDPG原始论文:https://zhuanlan.zhihu.com/p/53613085
https://zhuanlan.zhihu.com/p/111257402
https://www.cnblogs.com/pinard/p/10345762.html
https://cheersyouran.github.io/2018/06/17/pg/
https://www.zhihu.com/question/65005739
一、DDPG
- DDPG也是结合策略和值的强化学习算法,同样是以策略梯度作为最核心的框架,但是是从确定性策略梯度出发的。在值的部分也做了改造,使用了DQN作为Q的估计,所以也有人认为DDPG是DQN的延申,即Qlearning->DQN->DDPG
- DDPG的特点是指定了固定的输出,也就是Actor不再输出不同动作的概率,而是输出固定的值,更像一个控制器了
- DDPG已经是可以实际应用的算法了,所以在原始算法中使用了很多工程操作,比如缓存池、软更新等,这里不进行展开,
1、确定策略梯度
∇ J ( θ ) = E [ ∇ θ Q ( s , a ) ] = E [ α ( ∇ a Q ( s , a ) ∗ ∇ θ π ( s ) ) ] \nabla{J(\theta)} = E[ \nabla_{\theta}{Q(s,a)}]=E[ \alpha(\nabla_aQ(s,a)*\nabla_\theta{\pi(s)})] ∇J(θ)=E[∇θQ(s,a)]=E[α(∇aQ(s,a)∗∇θπ(s))]
- 这个公式看起来一步就推出来了,本身就是链式法则,没什么特别的
- 但其实隐含了一个问题这个Q的梯度是在目前策略导致状态分布下计算的,更改策略后状态分布就变化了,那这个梯度方向还能保证一定是优化的方向吗?后面的证明其实就证明了仍然是优化方向
推导如下:



2、算法框架
算法框架如下:
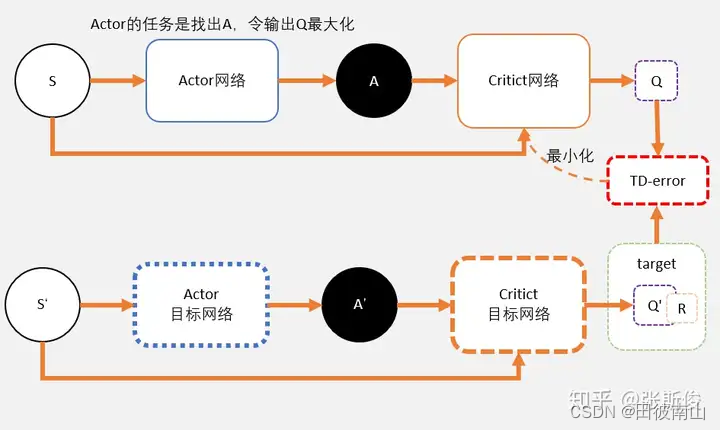
3、算法细节
(1)Critict网络
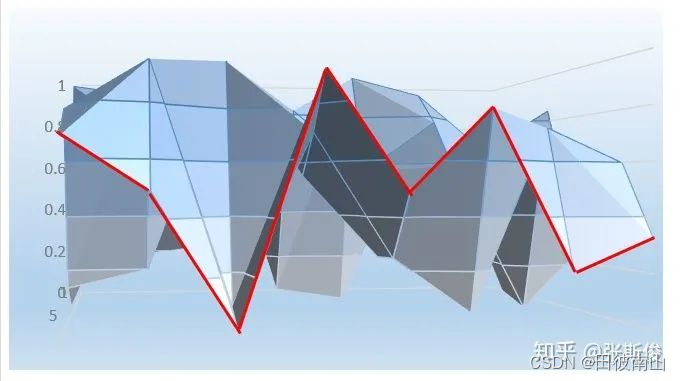
- Critict网络还是在拟合价值函数,不过这里拟合的就是动作状态价值函数了,也就是DQN拟合的那个函数,可以形象的理解为下面这个离散图上蒙上一块布,进而变为连续的。
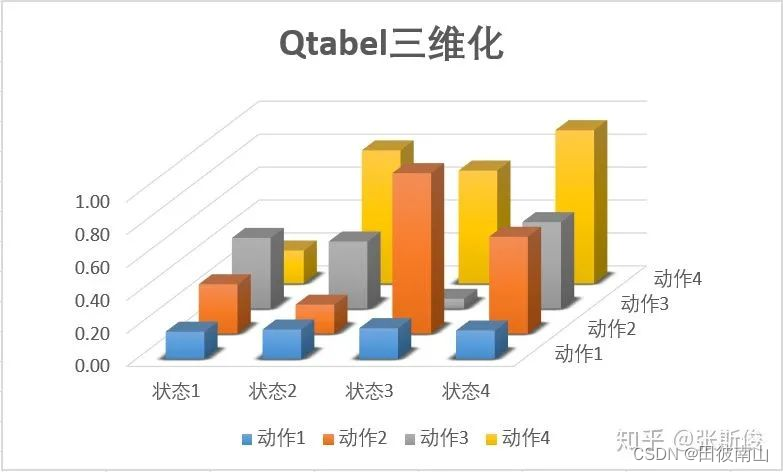
(2)Actor网络
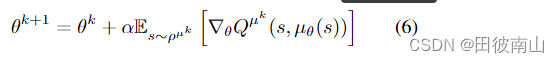
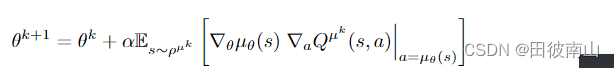
- actor实际上就是在找Q的最大值
(3)算法流程

4、物理理解
- 相较于随机策略梯度,确定策略梯度的物理理解比较直接,就是想找Q的梯度,直接最大化Q。
==============================================================================================
DDPG和随机策略梯度的比较:
确定策略梯度:理解为找最大的Q
∇ J ( θ ) = E [ ∇ θ Q ( s , a ) ] = E [ α ( ∇ a Q ( s , a ) ∗ ∇ θ π ( s ) ) ] \nabla{J(\theta)} = E[ \nabla_{\theta}{Q(s,a)}]=E[ \alpha(\nabla_aQ(s,a)*\nabla_\theta{\pi(s)})] ∇J(θ)=E[∇θQ(s,a)]=E[α(∇aQ(s,a)∗∇θπ(s))]
确定策略梯度:理解为“带权重的梯度”,G为代表好坏的权重, ∇ π \nabla{\pi} ∇π为代表方向的梯度(注意这个梯度跟目标函数梯度不同)
∇ J ( θ ) = E π [ ∇ l o g ( π θ ( s , a ) ) ∗ Q π ( s , a ) ] \nabla{J(\theta)}=E_{\pi}[\nabla{log(\pi_{\theta}(s,a))}*Q_{\pi}(s,a)] ∇J(θ)=Eπ[∇log(πθ(s,a))∗Qπ(s,a)]
- 二者都是基于目标函数的梯度上升延申出的算法,我不认为从DQN去理解DDPG更好。原始论文也说明,确定策略梯度是随机策略梯度的极限情况。
- 随机策略梯度更全面,既有基于MC的REINFORCE,也有基于TD的AC。而确定策略梯度则只有基于TD的DDPG,应该是因为Q的梯度没法采样获得吧











![[AI Google] 10个即将到来的Android生态系统更新](https://img-blog.csdnimg.cn/img_convert/eac1496c632b95c5eb8dca4a3d26ad9d.gif)