Python求解线性规划——PuLP使用教程
简洁是智慧的灵魂，冗长是肤浅的藻饰。——莎士比亚《哈姆雷特》

一、说明

PulP库是求解线性规划问题的python库，本篇告诉大家，如何使用这种库，用案例给出说明。

二、安装 PuLP 库

如果您使用的是 Anaconda[1] 的话（事实上我也更推荐这样做），需要先激活你想要安装的虚拟环境，之后在 Prompt 输入

pip install pulp

不出意外的话等一会就安装完毕。

三、线性规划简介

想必大家能点开这篇文章一定都知道线性规划是什么意思吧……那么我用两个例子再简单说一下。

3.1 线性规划

3.1.1 高考题目描述

若变量 x,y， 满足约束条件：
$$\{\begin{array}{rl}& 2x+3y-6\ge 0\\ & x+y-3\le 0\\ & y-2\le 0\end{array}$$

求 $z=3x+y$ 的最大值。

3.1.2 基本概念

首先，我们要认清在这道题中，x 和y 是可以变的，所以把它们叫做决策变量。三个不等式叫做约束条件，即 x 和 y 必须同时满足这三个不等式。我们若画出图来：

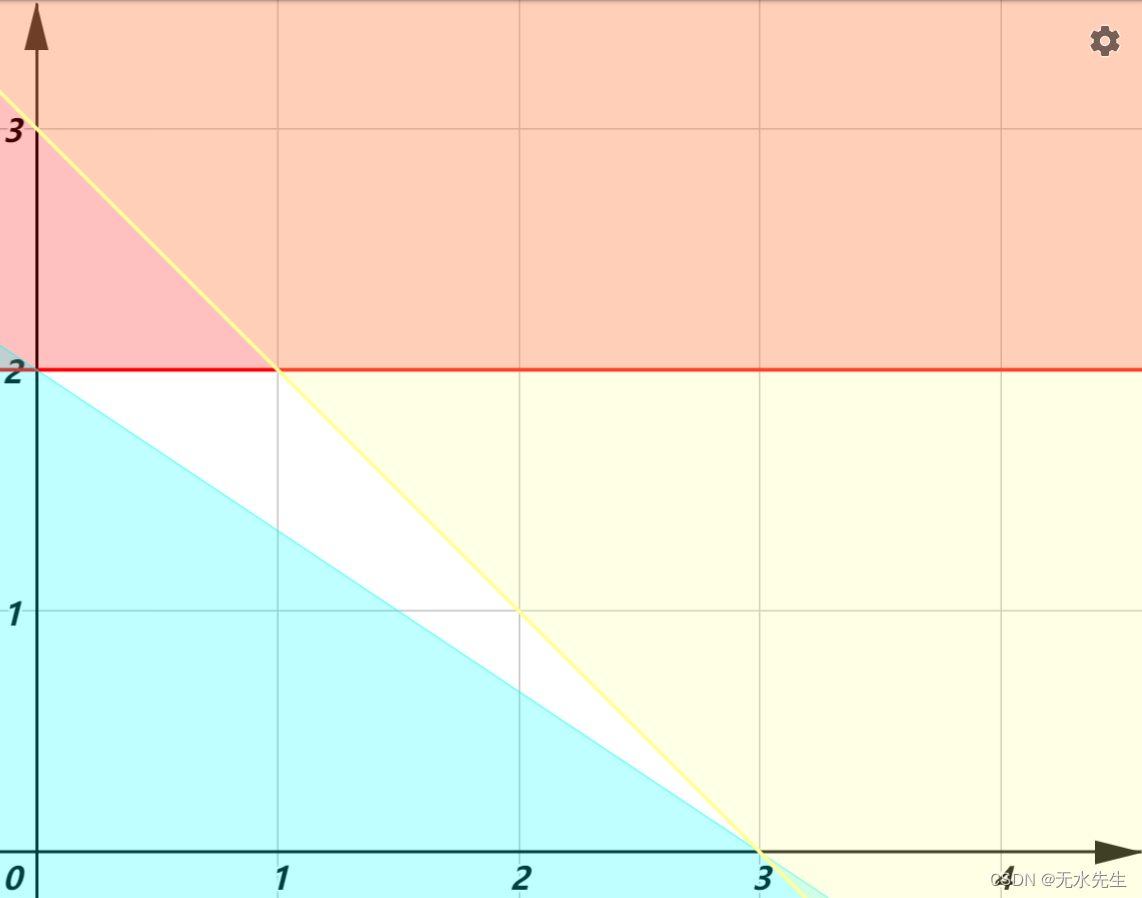
其中不满足约束条件的区域被我标上了颜色，所以 x,y 可以取得值只能在纯白区域内，这一片区域称作可行域。

再看最后的我们的目标：求 z=x+3y 的最大值。
于是 z=x+3y 就被称作目标函数，我们的工作就是求这个目标函数的最大值。

整个问题描述为：

然后怎么算？别急我们再看一个例子。

3.2 整数规划

3.2.1 题目描述[3]

汽车厂生产小、中、大三种类型的汽车，已知各类型每辆车对钢材、劳动时间的需求以及利润如下表所示。要求每月的钢材消耗不超过 600 t，总劳动时间不超过 60 000 h。试指定生产计划使得工厂每月的利润最大。

-	小型车	中型车	大型车
钢材 / t	1.5	3	5
劳动时间 / h	280	250	400
利润 / 万元	2	3	4

3.2.2 解题思路

首先，设三个决策变量，用x1,x2,x3 分别表示生产小型车、中型车、大型车的数量，但是注意要满足：

• 车的数量只能是整数；
• 车的数量大于等于 0。
  其他约束条件看题直接列：
  

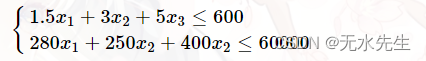
最后写出目标函数：
$$z=2x_1+3x_2+4x_3$$
综合起来整个问题描述为：

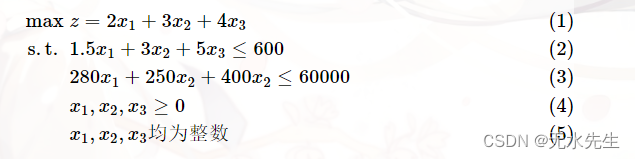
另外可以看出这个题由于涉及到三个决策变量，可行域是相当抽象的，这里就不画了 hhh~

四、求解过程

首先在最前面引入所需的pulp工具库：

import pulp as pl

这句话是引入 pulp 库并简写为 pl，一个 python 库只有在开始 import 了之后才能在后面使用。这样后面凡是用到 pulp 的功能都要写成 pl.xxx。

接下来是以下几个步骤：

• 定义模型
• 定义决策变量
• 添加约束条件
• 添加目标函数
• 模型求解
• 打印结果

4.1 定义模型

# Define the model
model = pl.LpProblem(name="My-Model", sense=pl.LpMaximize)

这个操作是使用 pl.LpProblem 创建了一个模型并赋值给变量 model，接收两个参数：

• name：模型的名字，随便起一个；
• sense：模型的类型，pl.LpMinimize是求目标函数的最小值，pl.LpMaximize 是求最大值

4.2 定义决策变量

# Define the decision variables
x = pl.LpVariable(name='x')
y = pl.LpVariable(name='y')

如果你的变量比较少的话可以简单这么写。这个意思是定义了两个浮点数变量，取值范围是整个实数域。注意等号左边的变量才是你在之后的计算式中使用的符号，而参数 name 只有在最后打印结果的时候才会被打印出来。另外如果你对变量有其他要求的话可以添加以下参数：

lowBound：变量的最小取值（不写的话默认负无穷）； upBound：变量的最大取值（默认正无穷）； cat：变量的类型，有
pl.Binary 逻辑变量、pl.Integer 整数、pl.Continuous 实数（默认值）；

如果你的变量比较多而不得不用 1, 2, 3…… 来编号，可以采用类似这样的写法：

# Define the decision variables
x = {i: pl.LpVariable(name=f"x{i}", lowBound=0, cat=pl.LpInteger) for i in range(1, 9)}

这是一次定义 8 个变量并保存在一个类似数组的结构中，变量都是正整数，分别用 x[1],x[2], …, x[8] 表示，依次命名为 x1, x2,…, x8。

注意 range(left, right) 表示的区间是左闭右开。

4.3 添加约束条件

# Add constraints
model += (2 * x + 3 * y - 6 >= 0, "constrain_1")
model += (x + 3 * y - 3 == 0, "constrain_2")

没错！如你所见就是这么简单，括号里第一个变量就是你的约束不等式或等式，第二个变量是你的自定义的约束名（可以起一个有意义的名字，当然也可以省略）。

由于一些比较数学的原因，约束条件里是不能使用大于号“>”或小于号“<”的。

如果你像前面一样把变量定义在了数组中，那么可以直接用方括号调用：

model += (2 * x[1] + 3 * x[2] - 6 >= 0)

4.4 添加目标函数

# Set the objective
model += x + 3 * y

与前面添加约束条件不同，添加目标函数这一步不用加最外层的括号。

4.5 模型求解

# Solve the optimization problem
status = model.solve()

就写这一句话，调用 model 的 solve() 方法，并把结果保存在 status 中。

 ## 4.4 打印结果# Get the results
print(f"status: {model.status}, {pl.LpStatus[model.status]}")
print(f"objective: {model.objective.value()}")for var in model.variables():print(f"{var.name}: {var.value()}")for name, constraint in model.constraints.items():print(f"{name}: {constraint.value()}")

然后你就能看到模型求解的结果了。

五、 示例代码

5.1 高考题代码

首先解决一下 3.1 的高考题：

import pulp as pl# 定义一个模型，命名为 "Model_3.1"，求最大值
model = pl.LpProblem(name="Model_3.1", sense=pl.LpMaximize)# 定义两个决策变量，取值为整个实数域
x = pl.LpVariable(name='x')
y = pl.LpVariable(name='y')# 添加三个约束条件
model += (2 * x + 3 * y - 6 >= 0)
model += (x + y - 3 <= 0)
model += (y - 2 <= 0)# 目标函数
model += x + 3 * y# 求解
status = model.solve()# 打印结果
print(f"status: {model.status}, {pl.LpStatus[model.status]}")
print(f"objective: {model.objective.value()}")for var in model.variables():print(f"{var.name}: {var.value()}")for name, constraint in model.constraints.items():print(f"{name}: {constraint.value()}")

查看结果的最后几行：

status: 1, Optimal objective: 7.0 x: 1.0 y: 2.0
_C1: 2.0
_C2: 0.0
_C3: 0.0

最大值是 7.0，在 x=1.0,y=2.0 时取到。

5.2 汽车厂代码

import pulp as pl# 定义一个模型，命名为 "Model_3.2"，求最大值
model = pl.LpProblem(name="Model_3.2", sense=pl.LpMaximize)# 定义三个决策变量，取值正整数
x = {i: pl.LpVariable(name=f"x{i}", lowBound=0, cat=pl.LpInteger) for i in range(1, 4)}# 添加约束条件
model += (1.5 * x[1] + 3 * x[2] + 5 * x[3] <= 600)
model += (280 * x[1] + 250 * x[2] + 400 * x[3] <= 60000)# 目标函数
model += 2 * x[1] + 3 * x[2] + 4 * x[3]# 求解
status = model.solve()# 打印结果
print(f"status: {model.status}, {pl.LpStatus[model.status]}")
print(f"objective: {model.objective.value()}")for var in model.variables():print(f"{var.name}: {var.value()}")for name, constraint in model.constraints.items():print(f"{name}: {constraint.value()}")

查看结果的最后几行：

status: 1, Optimal objective: 632.0 x1: 64.0 x2: 168.0 x3: 0.0
_C1: 0.0
_C2: -80.0

三种车的产量分别取 64、168、0，最大收益 632 万元。

六、结论

众所周知 Python 在各个领域如此受欢迎很大程度上是因为其有众多强大的第三方库，但是用的多了就会发现如果安装太多库就有点乱。而 Anaconda 就是一种很方便的管理 Python 环境的工具，不仅可以将不同的库分门别类管理好，更有用的是可以在电脑上安装不同版本的 Python 而不用担心会互相冲突。 ↩︎