论文链接:https://arxiv.org/abs/1808.09781
其他解读文章:https://mp.weixin.qq.com/s/cRQi3FBi9OMdO7imK2Y4Ew
摘要
顺序动态是许多现代推荐系统的一个关键特征,这些系统试图根据用户最近执行的操作来捕获用户活动的“上下文”。为了捕捉这种模式,两种方法已经激增:马尔可夫链(MC)和递归神经网络(RNN)。马尔可夫链假设用户的下一个动作可以仅根据他们最后(或最后几个)动作来预测,而 RNN 原则上允许发现长期语义。一般来说,基于 MC 的方法在极稀疏的数据集中表现最好,其中模型精简至关重要,而 RNN 在更密集的数据集中表现更好,在这些数据集中,模型复杂性更高。我们工作的目标是平衡这两个目标,通过提出一个基于自我注意力的顺序模型(SASRec),该模型允许我们捕获长期语义(如RNN),但是,使用注意力机制,根据相对较少的动作(如MC)进行预测。在每个时间步中,SASRec 都会尝试从用户的操作历史记录中确定哪些项目是“相关”的,并使用它们来预测下一个项目。广泛的实证研究表明,我们的方法在稀疏和密集数据集上都优于各种最先进的序列模型(包括基于 MC/CNN/RNN 的方法)。此外,该模型比基于CNN/RNN的可比较模型的效率高出一个数量级。注意力权重的可视化还显示了我们的模型如何自适应地处理具有不同密度的数据集,并在活动序列中发现有意义的模式。
1.引言
顺序推荐系统的目标是将用户行为的个性化模型(基于历史活动)与基于用户最近行为的“上下文”概念相结合。从顺序动态中捕获有用的模式具有挑战性,主要是因为输入空间的维度随着用作上下文的过去操作的数量呈指数增长。因此,顺序推荐的研究主要关注如何简洁地捕捉这些高阶动态。
马尔可夫链(MCs)是一个典型的例子,它假设下一个动作仅以前一个动作(或前几个动作)为条件,并已成功用于表征推荐的短程项目转换[1]。另一类工作使用递归神经网络(RNN)通过隐藏状态总结所有先前的动作,用于预测下一个动作[2]。
这两种方法虽然在特定情况下都很强大,但在某种程度上仅限于某些类型的数据。基于MC的方法通过进行强有力的简化假设,在高稀疏度设置中表现良好,但可能无法捕获更复杂场景的复杂动态。相反,RNN 虽然具有表现力,但需要大量数据(尤其是密集数据)才能优于更简单的基线。
最近,一种新的顺序模型Transfomer在机器翻译任务中实现了最先进的性能和效率[3]。与使用卷积或递归模块的现有顺序模型不同,Transformer 纯粹基于一种称为“自我注意力”的注意力机制,该机制非常高效,能够揭示句子中单词之间的句法和语义模式。
受这种方法的启发,我们试图将自我注意力机制应用于顺序推荐问题。我们希望这个想法可以解决上述两个问题,一方面能够从过去的所有行动中获取上下文(如RNN),另一方面能够仅根据少量行动(如MC)来构建预测。具体来说,我们建立了一个基于自我注意力的顺序推荐模型(SASRec),该模型在每个时间步自适应地为以前的项目分配权重(图1)。
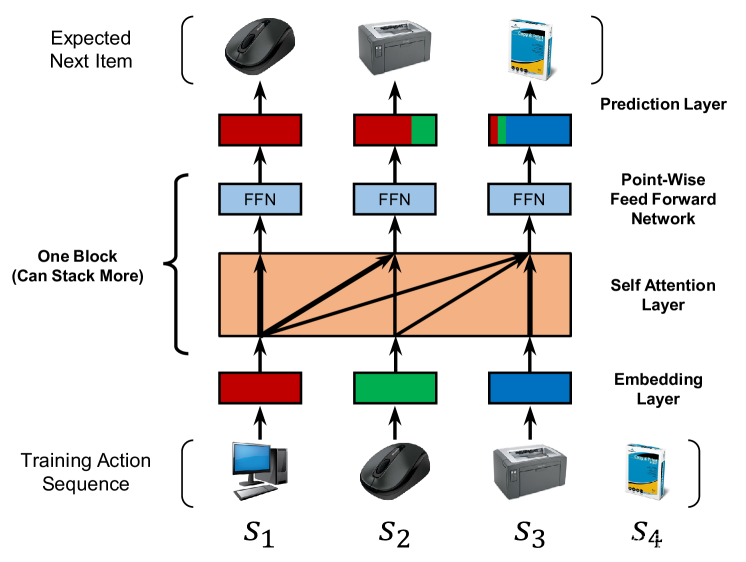
图 1:显示 SASRec 训练过程的简化图。在每个时间步中,模型都会考虑所有以前的项目,并使用注意力来“关注”与下一个操作相关的项目。
所提出的模型在几个基准数据集上明显优于最先进的基于 MC/CNN/RNN 的顺序推荐方法。特别是,我们将性能作为数据集稀疏性的函数进行研究,其中模型性能与上述模式密切相关。由于自注意力机制,SASRec倾向于考虑密集数据集上的长期依赖关系,同时关注稀疏数据集上的最新活动。事实证明,这对于自适应处理具有不同密度的数据集至关重要。
此外,SASRec 的核心组件(即自注意力块)适用于并行加速,从而使模型比基于 CNN/RNN 的替代方案快一个数量级。此外,我们分析了SASRec的复杂性和可扩展性,进行了全面的消融研究以显示关键组件的效果,并可视化了注意力权重以定性地揭示模型的行为。
2.相关工作
有几条工作线与我们密切相关。我们首先讨论一般性推荐,然后是时间性推荐,然后再讨论顺序推荐(特别是 MC 和 RNN)。最后,我们介绍注意力机制,特别是作为我们模型核心的自我注意力模块。
2-A 常规推荐
推荐系统专注于根据历史反馈(例如点击、购买、点赞)对用户和项目之间的兼容性进行建模。用户反馈可以是明确的(例如评分)或隐含的(例如点击、购买、评论)[ 4, 5]。由于解释“未观察到的”(例如未购买的)数据的模糊性,对隐式反馈进行建模可能具有挑战性。针对该问题,提出了逐点[4]和成对[5]方法来解决此类挑战。
矩阵分解(MF)方法试图揭示潜在维度,以表示用户的偏好和项目属性,并通过用户和项目嵌入之间的内积估计交互[6,7]。此外,另一项工作是基于项目相似性模型(ISM),并且没有明确地使用潜在因素对每个用户进行建模(例如FISM [ 8])。他们学习项目到项目的相似性矩阵,并通过测量项目与用户之前交互过的项目的相似性来估计用户对项目的偏好。
关于矩阵分解可以参考视频:https://www.bilibili.com/video/BV1gJ411m7Ym
基于项目相似性模型(ISM)是什么?
最近,由于深度学习技术在相关问题上的成功,各种深度学习技术被引入推荐[9]。其中一项工作试图使用神经网络来提取项目特征(例如图像 [10,11]、文本 [12,13] 等)以进行内容感知推荐。另一条工作线试图取代传统的MF。例如,NeuMF [14] 通过多层感知(MLP)估计用户偏好,而 AutoRec [15] 使用自动编码器预测评级。
[9]对基于深度学习的推荐系统的最新研究成果进行全面综述。
2-B 时序推荐
追溯到Netflix Prize数据集,通过明确建模用户活动的时间戳,时序推荐在各种任务中表现出强大的表现。TimeSVD++[16] 通过将时间分成几个段,并在每个段中分别对用户和项目进行建模,取得了很好的效果。这些模型对于理解表现出显着(短期或长期)时间“漂移”的数据集至关重要(例如,“过去 10 年电影偏好发生了怎样的变化”,或“用户在下午 4 点访问了什么样的企业?”等)[17, 18, 16]。顺序推荐(或下一物品推荐)与此设置略有不同,因为它只考虑操作的顺序,并对与时间无关的顺序模式进行建模。从本质上讲,顺序模型试图根据用户最近的活动来模拟用户行为的“上下文”,而不是考虑时间模式本身。
2-C 顺序推荐
许多顺序推荐系统试图将商品-商品转移矩阵建模,作为捕获连续项目之间顺序模式的一种手段。例如,FPMC融合了MF项和商品-商品转换项,以分别捕获长期偏好和短期转换[1]。从本质上讲,捕获的转移是一阶马尔可夫链 (MC),而高阶 MC 假设下一个动作与之前的几个动作相关。由于上次访问的商品通常是影响用户下一步行动的关键因素(本质上是提供“上下文”),因此基于一阶 MC 的方法表现出强大的性能,尤其是在稀疏数据集上 [19]。还有一些采用高阶MC的方法,考虑了更多的先前项目[20,21]。特别是,卷积序列嵌入(Caser)是一种基于CNN的方法,它将𝐿个之前的商品的嵌入矩阵视为“图像”,并应用卷积运算来提取转移[22]。
除了基于MC的方法外,另一项工作采用RNN来模拟用户序列[23,2,24,25]。例如,GRU4Rec 使用门控循环单元 (GRU) 对基于会话的推荐的点击序列进行建模 [2],改进的版本进一步提高了其 Top-N 推荐性能 [26]。在每个时间步中,RNN 将上一步的状态和当前操作作为其输入。这些依赖关系使RNN的效率降低,尽管已经提出了诸如“会话并行性”之类的技术来提高效率[2]。
2-D 注意力机制
注意力机制已被证明在各种任务中是有效的,例如图像标题[27]和机器翻译[28]等。从本质上讲,这种机制背后的思想是,每个顺序输出都依赖于某些输入的“相关”部分,这些部分是模型应依次关注的。另一个好处是,基于注意力的方法通常更容易解释。最近,注意力机制已被纳入推荐系统[29,30,31]。例如,注意力分解机(AFM)[30]学习每个特征交互对内容感知推荐的重要性。
然而,上面使用的注意力技术本质上是原始模型的附加组件(例如注意力+RNN、注意力+FMs等)。最近,一种纯粹基于注意力的序列到序列方法Transfomer[3]在机器翻译任务上实现了最先进的性能和效率,而这些任务以前由基于RNN/CNN的方法主导[32,33]。Transformer 模型在很大程度上依赖于所提出的“self-attention”模块来捕获句子中的复杂结构,并检索相关单词(源语言)以生成下一个单词(目标语言)。受Transformer的启发,我们试图建立一个基于自注意力方法的新顺序推荐模型,尽管顺序推荐的问题与机器翻译有很大不同,并且需要专门设计的模型。
3.方法论

在顺序推荐的设置中,我们给定一个用户的动作序列 S u = ( S 1 u , S 2 u , … , S ∣ S u ∣ u ) \mathcal{S}^u=\left(\mathcal{S}_1^u, \mathcal{S}_2^u, \ldots, \mathcal{S}_{\left|\mathcal{S}^u\right|}^u\right) Su=(S1u,S2u,…,S∣Su∣u),并试图预测下一个项目。在训练过程中,在时间步长𝑡,模型根据前𝑡项预测下一个项目。如图1 所示,可以方便地将模型的输入考虑为 ( S 1 u , S 2 u , … , S ∣ S u ∣ − 1 u ) \left(\mathcal{S}_1^u, \mathcal{S}_2^u, \ldots, \mathcal{S}_{\left|\mathcal{S}^u\right|-1}^u\right) (S1u,S2u,…,S∣Su∣−1u),将其预期输出视为同一序列的“移位”版本: ( S 2 u , S 3 u , … , S ∣ S u ∣ u ) \left(\mathcal{S}_2^u, \mathcal{S}_3^u, \ldots, \mathcal{S}_{\left|\mathcal{S}^u\right|}^u\right) (S2u,S3u,…,S∣Su∣u)。在本节中,我们将介绍如何通过嵌入层、多个自注意力块和预测层来构建顺序推荐模型。我们还分析了它的复杂性,并进一步讨论了SASRec与相关模型的不同之处。表一总结了我们的符号。
3-A 嵌入层
我们将训练序列 ( S 2 u , S 3 u , … , S ∣ S u ∣ u ) \left(\mathcal{S}_2^u, \mathcal{S}_3^u, \ldots, \mathcal{S}_{\left|\mathcal{S}^u\right|}^u\right) (S2u,S3u,…,S∣Su∣u)转换为固定长度序列 s = ( s 1 , s 2 , … , s n ) s=\left(s_1, s_2, \ldots, s_n\right) s=(s1,s2,…,sn),其中 n n n表示模型可以处理的最大长度。如果序列长度大于 n n n,则考虑最近的𝑛操作。如果序列长度小于𝑛,我们重复向左添加一个“填充”项,直到长度为𝑛。我们创建一个项目嵌入矩阵, M ∈ R ∣ J ∣ × d \mathbf{M} \in \mathbb{R}^{|\mathcal{J}| \times d} M∈R∣J∣×d,其中𝑑是潜在维数,并检索输入嵌入矩阵 E ∈ R n × d \mathbf{E} \in \mathbb{R}^{n \times d} E∈Rn×d,其中 E i = M s i \mathbf{E}_i=\mathbf{M}_{s_i} Ei=Msi。常量零向量𝟎用作填充项的嵌入。
位置嵌入
正如我们将在下一节中看到的,由于自注意力模型不包括任何递归或卷积模块,因此它不知道前面项目的位置。因此,我们将一个可学习的位置嵌入 P ∈ R n × d \mathbf{P} \in \mathbb{R}^{n \times d} P∈Rn×d注入到输入嵌入中:
E ^ = [ M s 1 + P 1 M s 2 + P 2 M s n + P n ] \hat{\mathbf{E}}=\left[\begin{array}{l}\mathbf{M}_{s_1}+\mathbf{P}_1 \\ \mathbf{M}_{s_2}+\mathbf{P}_2 \\ \mathbf{M}_{s_n}+\mathbf{P}_n\end{array}\right] E^= Ms1+P1Ms2+P2Msn+Pn
我们还尝试了[3]中使用的固定位置嵌入,但发现这会导致我们示例中的性能变差。我们在实验中定量和定性地分析了位置嵌入的影响。
[3]是transformer
3-B 自注意力块
The scaled dot-product attention [3] is defined as:
A t t e n t i o n ( Q , K , V ) = softmax ( Q K T d ) V Attention (\mathbf{Q}, \mathbf{K}, \mathbf{V})=\operatorname{softmax}\left(\frac{\mathbf{Q} \mathbf{K}^T}{d}\right) \mathbf{V} Attention(Q,K,V)=softmax(dQKT)V
其中 Q Q Q表示查询、 K K K键和 V V V值(每行表示一个项目)。直观地,注意力层计算所有值的加权和,其中查询𝑖
和值𝑗之间的权重与查询𝑖和键𝑗之间的交互有关。比例因子𝑑是为了避免内积值过大,尤其是在维数较高时。
Self-Attention layer
在机器翻译等NLP任务中,注意力机制通常使用𝐊=𝐕(例如使用RNN编码器-解码器进行翻译:编码器的隐藏状态是键和值,解码器的隐藏状态是查询)[28]。最近,人们提出了一种自注意力方法,它使用同一个对象作为查询、键和值[3]。在我们的例子中,自注意力操作将嵌入 E ^ \hat{\mathbf{E}} E^作为输入,通过线性投影将其转换为三个矩阵,并将它们输入到注意力层中:
S = S A ( E ^ ) = Attention ( E ^ W Q , E ^ W K , E ^ W V ) \mathbf{S}=\mathrm{SA}(\hat{\mathbf{E}})=\operatorname{Attention}\left(\hat{\mathbf{E}} \mathbf{W}^Q, \hat{\mathbf{E}} \mathbf{W}^K, \hat{\mathbf{E}} \mathbf{W}^V\right) S=SA(E^)=Attention(E^WQ,E^WK,E^WV)
其中投影矩阵 W Q , W K , w V ∈ R d × d \mathbf{W}^Q, \mathbf{W}^K, \mathbf{w}^V \in \mathbb{R}^{d \times d} WQ,WK,wV∈Rd×d,投影使模型更加灵活。例如,模型可以学习非对称交互(即<𝑖查询、键𝑗>和<查询𝑗、键𝑖>可以有不同的交互)。
Causality(因果关系)
由于序列的性质,模型在预测第 (𝑡+1)项时应仅考虑前面𝑡项。但是,自注意层( S t S_t St)的第t个输出包含后续项的嵌入,这使得模型ill-poesd(病态)。因此,我们通过禁止 Q i Q_i Qi和 K j ( j > i ) K_j(j>i) Kj(j>i)之间的所有链接来修改注意力。
Point-Wise Feed-Forward Network(逐点前馈网络)
尽管自注意力能够用自适应权重聚合所有先前项目的嵌入,但最终它仍然是一个线性模型。为了赋予模型非线性并考虑不同潜在维度之间的相互作用,我们将把一个逐点的两层的前馈网络应用于所有 S i S_i Si(共享参数):
F i = FFN ( S i ) = ReLU ( S i W ( 1 ) + b ( 1 ) ) W ( 2 ) + b ( 2 ) \mathbf{F}_i=\operatorname{FFN}\left(\mathbf{S}_i\right)=\operatorname{ReLU}\left(\mathbf{S}_i \mathbf{W}^{(1)}+\mathbf{b}^{(1)}\right) \mathbf{W}^{(2)}+\mathbf{b}^{(2)} Fi=FFN(Si)=ReLU(SiW(1)+b(1))W(2)+b(2)
其中 W ( 1 ) \mathbf{W}^{(1)} W(1), W ( 2 ) \mathbf{W}^{(2)} W(2)是 d × d d\times d d×d矩阵, b ( 1 ) \mathbf{b}^{(1)} b(1), b ( 1 ) \mathbf{b}^{(1)} b(1)是 d d d维向量。请注意, S i S_i Si和 S j S_j Sj没有交互,这意味着我们仍然防止信息泄露(从后到前)。
3-C 堆叠自注意力block
在第一个自注意力块之后, F i F_i Fi基本上聚合了所有先前项的嵌入(即 E ^ j , j ≤ i \hat{\mathbf{E}}_j, j \leq i E^j,j≤i)。但是,可能可以通过另一个基于 F F F的自注意力块来学到更复杂的item转换。具体来说,我们堆叠了自注意力块(即自注意力层和前馈网络),第 b b b层block被定义为:
S ( b ) = S A ( F ( b − 1 ) ) F i ( b ) = F F N ( S i ( b ) ) , ∀ i ∈ { 1 , 2 , … , n } , \begin{gathered} \mathbf{S}^{(b)}=\mathrm{SA}\left(\mathbf{F}^{(b-1)}\right) \\ \mathbf{F}_i^{(b)}=\mathrm{FFN}\left(\mathbf{S}_i^{(b)}\right), \quad \forall i \in\{1,2, \ldots, n\}, \end{gathered} S(b)=SA(F(b−1))Fi(b)=FFN(Si(b)),∀i∈{1,2,…,n},
第一个block定义为: S ( 1 ) = S \mathbf{S}^{(1)}=\mathbf{S} S(1)=S, F ( 1 ) = F \mathbf{F}^{(1)}=\mathbf{F} F(1)=F。
然而,当网络深入时,几个问题会加剧:1)模型容量的增加导致过拟合; 2)训练过程变得不稳定(由于梯度消失等); 3)具有更多参数的模型通常需要更多的训练时间。受[3]的启发,我们执行以下操作来缓解这些问题:
g ( x ) = x + Dropout ( g ( LayerNorm ( x ) ) ) g(x)=x+\operatorname{Dropout}(g(\text { LayerNorm }(x))) g(x)=x+Dropout(g( LayerNorm (x)))
其中𝑔(𝑥)表示自注意力层或前馈网络。也就是说,对于每个块中的层𝑔,我们在馈入𝑔的输入之前对输入𝑥应用层归一化,在𝑔的输出上应用 dropout,并将输入𝑥添加到最终输出中。下面我们将介绍这些操作。
Residual Connections(残差连接)
在某些情况下,多层神经网络已经证明了分层学习有意义特征的能力[34]。然而,在提出残差网络之前,简单地添加更多层并不容易获得更好的性能[35]。残差网络背后的核心思想是通过残差连接将低层特征传播到更高层。因此,如果低层特征有用,则模型可以轻松地将它们传播到最后一层。同样,我们假设残差连接在我们的案例中也很有用。例如,现有的顺序推荐方法表明,上次访问的项目在预测下一个项目方面起着关键作用[1,21,19]。但是,经过几次自我关注块后,上次访问的项目的嵌入与之前的所有项目纠缠在一起;添加残差连接以将上次访问项的嵌入传播到最终层将使模型更容易利用低层信息。
layer normalization(层归一化)
层归一化用于对跨特征(即零均值和单位方差)的输入进行归一化,有利于稳定和加速神经网络训练[36]。与批量归一化不同[37],层归一化中使用的统计量独立于同一批次中的其他样本。具体而言,假设输入是包含样本所有特征的向量𝐱,则操作定义为
LayerNorm ( x ) = α ⊙ x − μ σ 2 + ϵ + β , \operatorname{LayerNorm}(\mathbf{x})=\alpha \odot \frac{\mathbf{x}-\mu}{\sigma^2+\epsilon}+\boldsymbol{\beta} \text {, } LayerNorm(x)=α⊙σ2+ϵx−μ+β,
其中 ⊙ \odot ⊙是逐元素乘积(哈达玛积), μ \mu μ和 σ \sigma σ是 x \mathbf{x} x的均值和标准差, α \alpha α和 β \beta β是要学习的比例因子和偏差项。
关于Layer norm和Batch Norm,推荐看李沐讲解transformer视频的26:00开始的内容。
Dropout
为了缓解深度神经网络中的过拟合问题,“Dropout”正则化技术已被证明在各种神经网络架构中是有效的[38]。Dropout的想法很简单:在训练过程中以𝑝的概率随机“关闭”神经元,并在测试时使用所有神经元。进一步的分析指出,Dropout可以被看作是集成学习的一种形式,它考虑了大量共享参数的模型(神经元数量和输入特征呈指数级增长)[39]。我们还在embedding E ^ \hat{\mathbf{E}} E^上应用了一个dropout 层。
3-D 预测层
在𝑏个自适应和分层提取以前消费的项目信息的自注意力块之后,我们根据 F t ( b ) \mathbf{F}_t^{(b)} Ft(b)预测下一个项目(给定前 t t tt个项目)。具体来说,我们采用MF层来预测项目𝑖的可能性:
r i , t = F t ( b ) N i T r_{i, t}=\mathbf{F}_t^{(b)} \mathbf{N}_i^T ri,t=Ft(b)NiT
其中 r i , t r_{i, t} ri,t是给定前𝑡项目(即 s 1 , s 2 , … , s t s_1,s_2, \ldots, s_t s1,s2,…,st)时,下一个项目与项目i的相关性。并且 N ∈ R ∣ J ∣ × d \mathbf{N} \in \mathbb{R}^{|\mathcal{J}| \times d} N∈R∣J∣×d是项目嵌入矩阵。因此,高互动分数 r i , t r_{i, t} ri,t意味着高相关性,我们可以通过对分数进行排名来生成建议。
这里的 N \mathbf{N} N虽然也是项目嵌入矩阵,但是他和 M \mathbf{M} M不一样。他也是需要学习的。(不过下一节马上就提到了,为了减小模型大小,不使用需要学习的N矩阵)
注意,这里的T是转置
共享项目embedding
为了减小模型大小并缓解过拟合,我们考虑了另一种只使用单个项目嵌入的方案
𝐌:
r i , t = F t ( b ) M i T r_{i, t}=\mathbf{F}_t^{(b)} \mathbf{M}_i^T ri,t=Ft(b)MiT
请注意, F t ( b ) \mathbf{F}_t^{(b)} Ft(b)可以表示为取决于嵌入矩阵 M \mathbf{M} M的函数: F t ( b ) = f ( M s 1 , M s 2 , … , M s t ) \mathbf{F}_t^{(b)}=f\left(\mathbf{M}_{s_1}, \mathbf{M}_{s_2}, \ldots, \mathbf{M}_{s_t}\right) Ft(b)=f(Ms1,Ms2,…,Mst)。使用同构项嵌入的一个潜在问题是,它们的内积不能表示不对称项转换(例如,项目𝑖经常在项目𝑗后购买,反之则不然),因此 FPMC 等现有方法倾向于使用异构项嵌入。但是,我们的模型没有这个问题,因为它学习非线性变换。例如,前馈网络在使用相同的项目嵌入的情况下,也可以很容易地实现不对称性: FFN ( M i ) M j T ≠ FFN ( M j ) M i T \operatorname{FFN}\left(\mathbf{M}_i\right) \mathbf{M}_j^T \neq \operatorname{FFN}\left(\mathbf{M}_j\right) \mathbf{M}_i^T FFN(Mi)MjT=FFN(Mj)MiT。根据经验,使用共享项嵌入可以显著提高模型的性能。
显式用户建模
为了提供个性化的推荐,现有方法通常采用以下两种方法之一:1)学习表示用户偏好的显式用户嵌入(例如MF[40],FPMC[1]和Caser[22]);2)考虑用户之前的行为,并从已经访问的项目的嵌入中推导出隐式的用户的嵌入(例如FSIM [8],Fossil [21],GRU4Rec [2])。我们的方法属于后一类,因为我们通过考虑用户的所有操作来生成嵌入 F n ( b ) \mathbf{F}_n^{(b)} Fn(b)。但是,我们也可以在最后一层插入一个显式的用户嵌入,例如,通过加法:
r u , i , t = ( U u + F t ( b ) ) M i T r_{u, i, t}=\left(\mathbf{U}_u+\mathbf{F}_t^{(b)}\right) \mathbf{M}_i^T ru,i,t=(Uu+Ft(b))MiT
其中, U \mathbf{U} U是一个用户嵌入矩阵。但是,我们根据经验发现,添加显式用户嵌入并不能提高性能(可能是因为模型已经考虑了用户的所有操作)。
3-E 网络训练
回想一下,我们通过截断或填充项目将每个用户序列(不包括最后一个操作) ( S 1 u , S 2 u , … , S ∣ S u ∣ − 1 u ) \left(\mathcal{S}_1^u, \mathcal{S}_2^u, \ldots, \mathcal{S}_{\left|S^u\right|-1}^u\right) (S1u,S2u,…,S∣Su∣−1u)转换为固定长度的序列 s = { s 1 , s 2 , … , s n } s=\left\{s_1, s_2, \ldots, s_n\right\} s={s1,s2,…,sn}。我们定义 o t o_t ot为时间步长 𝑡的预期输出:
o t = { < pad > if s t is a padding item s t + 1 1 ≤ t < n S ∣ δ u ∣ u t = n o_t=\left\{\begin{array}{l}<\text { pad }>\text { if } s_t \text { is a padding item } \\ s_{t+1} \quad 1 \leq t<n \\ \mathcal{S}_{\left|\delta^u\right|}^u \quad t=n\end{array}\right. ot=⎩ ⎨ ⎧< pad > if st is a padding item st+11≤t<nS∣δu∣ut=n
其中 < p a d > <pad> <pad>表示填充项。我们的模型将一个序列𝑠作为输入,将相应的序列𝑜作为预期输出,并采用二元交叉熵损失作为目标函数:
− ∑ s u ∈ s ∑ t ∈ [ 1 , 2 , … , n ] [ log ( σ ( r o t , t ) ) + ∑ j ∉ s u log ( 1 − σ ( r j , t ) ) ] -\sum_{s^u \in s} \sum_{t \in[1,2, \ldots, n]}\left[\log \left(\sigma\left(r_{o_t, t}\right)\right)+\sum_{j \notin s^u} \log \left(1-\sigma\left(r_{j, t}\right)\right)\right] −su∈s∑t∈[1,2,…,n]∑ log(σ(rot,t))+j∈/su∑log(1−σ(rj,t))
请注意,我们忽略了其中 o t = < o_t=< ot=< pad > > >的术语。
交叉熵损失函数建议参考视频:https://www.bilibili.com/video/BV1nK4y1w7ch
论文是将预测输出为 o t o_t ot的部分作为正例,预测输出位 j j j的部分作为反例,加入到loss中考虑。其中反例中的 j j j不能来自交互序列。这意味着反例都对应那些没有出现在交互序列的项。
该网络由 Adam 优化器 [41] 优化,它是具有自适应矩估计的随机梯度下降 (SGD) 的变体。在每个epoch中,我们为每个序列中的每个时间步随机生成一个负项目𝑗。稍后将介绍更多实现细节。
3-F 复杂度分析
空间复杂度
我们模型中学习到的参数来自自注意力层、前馈网络和层归一化中的嵌入和参数。参数总数为 O ( ∣ J ∣ d + n d + d 2 ) O\left(|\mathcal{J}| d+n d+d^2\right) O(∣J∣d+nd+d2),与其他方法(例如FPMC中的 O ( ∣ U ∣ d + ∣ J ∣ d ) O(|\mathcal{U}| d+|\mathcal{J}| d) O(∣U∣d+∣J∣d))相比,这是适中的,因为它不会随着用户数量的增加而增长,并且𝑑在推荐问题中通常很小。
从这里我知道了,self-attention layer中的embedding也是要学习的
这里有一个疑问,为什么会有参数量 n × d n\times d n×d?
时间复杂度
我们模型的计算复杂度主要归因于自注意力层和前馈网络,即 O ( n 2 d + n d 2 ) O\left(n^2 d+n d^2\right) O(n2d+nd2)。主导项 O ( n 2 d ) O\left(n^2 d\right) O(n2d)来自self-atttention layer。但是, 在我们的模型中,一个方便的特性是,每个自注意力层中的计算都是完全可并行化的,这适用于 GPU 加速。相比之下,基于RNN的方法(例如GRU4Rec [ 2])依赖于时间步长(即,时间步𝑡长上的计算必须等待时间步𝑡-1长的结果),这导致了顺序操作 O ( n ) O(n) O(n)的时间。我们根据经验发现,我们的方法比基于 RNN 和 CNN 的 GPU 方法快 10 倍以上(结果与[3] 中机器翻译任务的结果相似),并且最大长度 𝑛可以很容易地扩展到几百个,这对于现有的基准数据集来说通常已经足够了。
一般地,矩阵 A ∈ R m × n A\in R^{m\times n} A∈Rm×n和矩阵 B ∈ R n × l B\in R^{n\times l} B∈Rn×l乘积的时间复杂度是 m n l mnl mnl。
在测试过程中,对于每个用户来说,在计算嵌入 F n ( b ) \mathbf{F}_n^{(b)} Fn(b)后,过程与标准MF方法相同。(𝑂(𝑑)用于评估对项目的偏好)。
处理长序列
尽管我们的实验从经验上验证了我们方法的有效性,但最终它无法扩展到很长的序列。未来有几种选择有望进行研究:1)使用有限的自我注意力[42],它只关注最近的行动而不是所有的行动,并且可以在更高层次上考虑远距离行动;2)将长序列拆分为短片段,如[22]。
3-G 讨论
我们发现 SASRec 可以看作是一些经典 CF 模型的泛化。我们还从概念上讨论了我们的方法和现有方法如何处理序列建模。
简化得到现有模型
-
因式分解马尔可夫链(FMC):FMC对一阶项转移矩阵进行因式分解,并根据最后一项 i i i预测下一项 j j j:
P ( j ∣ i ) ∝ M i T N j P(j \mid i) \propto \mathbf{M}_i^T \mathbf{N}_j P(j∣i)∝MiTNj… -
因式分解项目相似性模型(FISM)[8]:FISM通过考虑用户之前消费的项目和𝑖项目的相似性来估计对项目的𝑖偏好分数。…
这一部分讲的是SASRec是现有的CF模型的泛化。因为对这些CF模型不熟悉,故暂略。
基于MC的推荐
马尔可夫链 (MC) 可以有效地捕获局部顺序模式,假设下一个项目仅依赖于前 𝐿项目。现有的基于MC的顺序推荐方法依赖于一阶MC(例如FPMC [ 1],HRM [ 43],TransRec [ 19])或高阶MC(例如Fossil [ 21],Vista [ 20],Caser [ 22])。第一组方法往往在稀疏数据集上表现最佳。相比之下,基于高阶MC的方法有两个局限性:(1)MC的阶𝐿需要在训练前指定,而不是自适应选择;(2)性能和效率不能很好地与订单 𝐿 成比例,因此
𝐿 通常很小(例如小于5)。我们的方法解决了第一个问题,因为它可以自适应地关注相关的先前项目(例如,只关注稀疏数据集上的最后一个项目,而关注密集数据集上的更多项目)。此外,我们的模型基本上是以𝑛以前的项目为条件的,并且可以经验地扩展到数百个以前的项目,随着训练时间的适度增加,表现出性能提升。
基于RNN的推荐
另一类工作是寻求使用RNN对用户动作序列进行建模[2,26,17]。RNN通常适用于序列建模,但最近的研究表明,在某些顺序设置中,CNN和自我注意力可能更强[3,44]。我们基于自注意力的模型可以从项目相似性模型中推导出来,这是推荐序列建模的合理替代方案。对于 RNN,除了它们在并行计算中的效率低下(第 III-F 节)之外,它们的最大路径长度(从输入节点到相关输出节点)为𝑂(𝑛)。相比之下,我们的模型具有𝑂(1)最大路径长度,这有利于学习长程依赖关系[45]。
4.实验
在本节中,我们介绍了我们的实验设置和实证结果。我们的实验旨在回答以下研究问题:
RQ1:SASRec 是否优于最先进的模型,包括基于 CNN/RNN 的方法?
RQ2:SASRec 架构中各种组件的影响是什么?
RQ3:SASRec的训练效率和可扩展性(关于𝑛)如何?
RQ4:注意力权重是否能够学习与位置或项目属性相关的有意义的模式?
4-A 数据集
我们在来自三个真实世界应用程序的四个数据集上评估了我们的方法。数据集在域、平台和稀疏性方面差异很大:
-
亚马逊:一系列数据集在[46]中被引入,包括从 Amazon.com 中抓取的大量产品评论语料库。
亚马逊上的顶级商品分类被视为单独的数据集。我们考虑两个类别,“Beauty”和“Games”。该数据集以其高稀疏性和可变性而著称。 -
Steam:我们引入了一个从大型在线视频游戏分发平台 Steam 抓取的新数据集。该数据集包含 2010 年 10 月至 2018 年 1 月的 2,567,538 名用户、15,474 款游戏和 7,793,069 条英文评论。该数据集还包括可能对未来工作有用的丰富信息,例如用户的游戏时间、定价信息、媒体评分、类别、开发者等。
-
MovieLens:一个广泛使用的基准数据集,用于评估协同过滤算法。我们使用包含 100 万用户评分的版本 (MovieLens-1M)。
我们遵循了与 [19,21,1] 相同的预处理过程。对于所有数据集,我们将评论或评级的存在视为隐式反馈(即用户与项目互动),并使用时间戳来确定操作的顺序。我们会丢弃相关操作少于 5 个的用户和项目。对于分区,我们将每个用户的历史序列 S u \mathcal{S}^u Su分为三个部分:(1)用于测试的最新操作 S ∣ S u ∣ u \boldsymbol{S}_{\left|\mathcal{S}^u\right|}^u S∣Su∣u, (2)用于验证的第二个最新操作 S ∣ S u ∣ − 1 u \mathcal{S}_{\left|\mathcal{S}^u\right|-1}^u S∣Su∣−1u,以及(3)用于训练的所有剩余操作。请注意,在测试期间,输入序列包含训练操作和验证操作。
数据统计如表二所示。我们看到,两个亚马逊数据集的每位用户和每件商品的操作次数最少(平均),Steam 的每件商品的平均操作数很高,而 MovieLens-1m 是最密集的数据集。

4-B 比较方法
为了证明我们方法的有效性,我们纳入了三组推荐基线。第一组包括一般推荐方法,这些方法只考虑用户反馈,而不考虑操作的顺序:
-
PopRec:这是一个简单的基线,根据项目的受欢迎程度(即相关操作的数量)对项目进行排名。
-
贝叶斯个性化排名(BPR)[5]:BPR是从隐式反馈中学习个性化排名的经典方法。偏置矩阵分解用作基础推荐器。
第二组包含基于一阶马尔可夫链的顺序推荐方法,这些方法考虑了最新访问的项目:
- 因式分解马尔科夫链(FMC):一阶马尔可夫链方法。FMC 使用两个项目嵌入对项目转换矩阵进行分解,并仅根据上次访问的项目生成建议。
- 因式分解个性化马尔可夫链 (FPMC) [ 1]:FPMC 使用矩阵分解和因式分解一阶马尔可夫链的组合作为其推荐器,它捕获用户的长期偏好以及项目到项目的转换。
- 基于翻译的推荐 (TransRec) [19]:一种最先进的一阶顺序推荐方法,它将每个用户建模为翻译向量,以捕获从当前项目到下一个项目的过渡。
最后一组包含基于深度学习的顺序推荐系统,该系统考虑了几个(或所有)以前访问过的项目:
- GRU4Rec [2]:一种开创性的方法,它使用 RNN 对用户操作序列进行建模,以便进行基于会话的推荐。我们将每个用户的反馈序列视为一个会话。
- GRU4Rec+ [26]:GRU4Rec 的改进版本,它采用了不同的损失函数和采样策略,并在 Top-N 推荐中显示出显着的性能提升。
- 卷积序列嵌入(Caser) [ 22]:最近提出的一种基于 CNN 的方法,通过对最新项目的嵌入矩阵𝐿应用卷积运算来捕获高阶马尔可夫链,并实现了最先进的顺序推荐性能。
由于其他顺序推荐方法(例如PRME [ 47]、HRM [ 43]、Fossil [ 21])在上述数据集的基线上表现优于其他方法,因此我们省略了与它们的比较。我们也不包括 TimeSVD++ [ 16] 和 RRN [ 17] 等时间推荐方法,它们在设置上与我们这里考虑的有所不同。
为了公平地比较,我们使用 TemsorFlow 和 Adam [ 41] 优化器来实现 BPR、FMC、FPMC 和 TransRec。对于 GRU4Rec、GRU4Rec+和 Caser,我们使用相应作者提供的代码。对于除 PopRec 之外的所有方法,我们从 { 10 , 20 , 30 , 40 , 50 } \{10,20,30,40,50\} {10,20,30,40,50}考虑潜在维度𝑑。对于 BPR、FMC、FPMC 和 TransRec,
ℓ 2 ℓ_2 ℓ2正则化器从 { 0.0001 , 0.001 , 0.01 , 0.1 , 1 } \{0.0001,0.001,0.01,0.1,1\} {0.0001,0.001,0.01,0.1,1}中选择。所有其他超参数和初始化策略都是方法作者建议的策略。我们使用验证集调整超参数,如果验证性能在 20 个周期内没有提高,则终止训练。
4-C 实施细节
对于 SASRec 默认版本中的架构,我们使用两个自注意力块 (𝑏=2),并使用学习的位置嵌入。嵌入层和预测层中的项目嵌入是共享的。我们使用TensorFlow 实现 SASRec。优化器是 Adam 优化器 [41],学习速率设置为0.001,批大小为128。由于 MovieLens-1m 的稀疏性,关闭神经元的dropout率为0.2,其他三个数据集的dropout率为 0.5。MovieLens-1m 的最大序列长度设置为 200,其他三个数据集的最大序列长度 𝑛设置为 50,即与每个用户的平均操作数大致成正比。下面将检查变体和不同超参数的性能。
4-D 评估指标
我们采用两个常见的Top-N指标,即命中Rate@10和NDCG@10来评估推荐效果[14,19]。Hit@10计算了ground truth出现在前 10 个预测的项目中的次数,而NDCG@10是一个位置感知指标,它在更高的位置上分配更大的权重。请注意,由于我们每个用户只有一个测试项目,因此Hit@10等同于Recall@10,并且与Precision@10成正比。
为了避免对所有用户-项目对进行大量计算,我们遵循了 [48,14] 中的策略。对于每个用户𝑢,我们随机抽取 100 个负项目,并将这些项目与真实项目进行排名。根据这 101 个项目的排名,可以评估Hit@10和NDCG@10。
4-E 推荐表现
RQ1:SASRec 是否优于最先进的模型,包括基于 CNN/RNN 的方法?
表III显示了所有方法在四个数据集(RQ1)上的推荐性能。通过考虑所有数据集中的次优方法,出现了一种一般模式,即非神经方法(即(a)-(e))在稀疏数据集上表现更好,而神经方法(即(f)-(h))在更密集的数据集上表现更好。据推测,这是由于神经方法具有更多的参数来捕获高阶跃迁(即,它们具有表现力但容易过拟合),而精心设计但更简单的模型在高稀疏性环境中更有效。
表三:推荐表现。每行中性能最好的方法以粗体显示,每行中的第二种最佳方法下划线显示。最后两列分别显示了对非神经方法和神经方法的改进。

最后两列分别值得是SASRec对比a-e中最好的模型的提升和f-h最好的模型的提升。
我们的方法 SASRec 在稀疏和密集数据集上的表现都优于所有基线,并且与最强基线相比,平均获得了6.9% 的命中率和 9.6%的NDCG改进。一个可能的原因是,我们的模型可以自适应地处理不同数据集上不同范围内的项目(例如,在稀疏数据集上仅关注前一项,而在密集数据集上则更多)。我们在第四节-H节中进一步分析了这种行为。
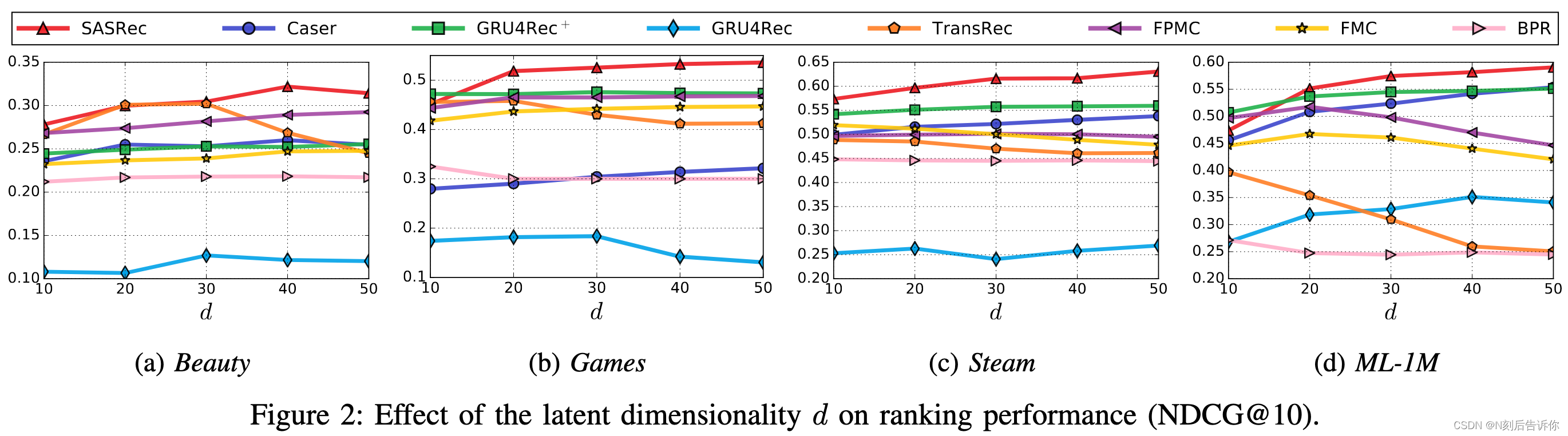
在图2中,我们显示了𝑑从10到50不等时,所有方法的NDCG@10,并分析了一个关键超参数,潜在维数𝑑的影响。我们看到,我们的模型通常受益于大量的潜在维度。对于所有数据集,在𝑑≥40时,我们的模型都实现了令人满意的性能。
4-F 消融实验
SASRec 架构中各种组件的影响是什么?
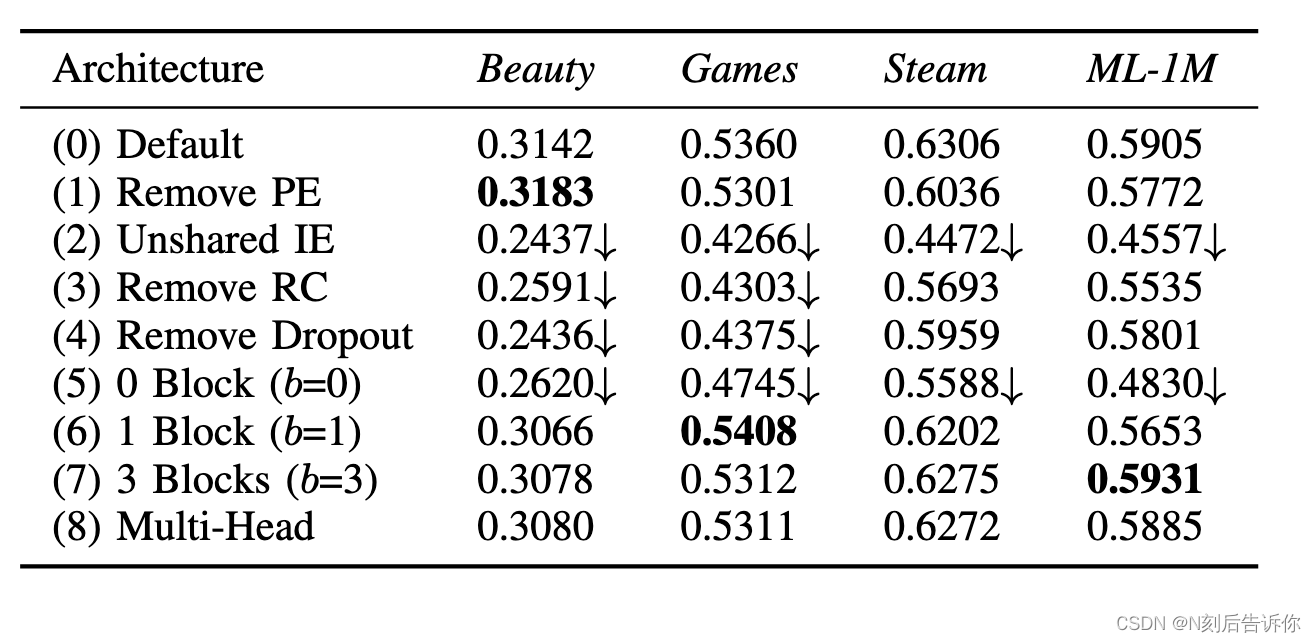
由于我们的架构中有许多组件,我们通过消融研究分析它们的影响(RQ2)。表 IV 显示了我们的默认方法及其 8 个变体在所有四个数据集上的性能(使用𝑑=50)。我们分别介绍了这些变体并分析了它们的效果:
表IV:四个数据集的消融分析(NDCG@10)。性能优于默认版本为粗体。‘↓’ 表示性能严重下降(超过 10%)。
-
(1) 删除 PE(位置嵌入):没有位置嵌入𝐏,每个项目的注意力权重仅取决于项目嵌入。也就是说,该模型根据用户过去的行为提出建议,但他们的顺序并不重要。此变体可能适用于用户序列通常较短的稀疏数据集。此变体在最稀疏数据集 (Beauty) 上的性能优于默认模型,但在其他更密集的数据集上表现更差。
-
2) 非共享 IE(项目嵌入):我们发现
使用两个项目嵌入会持续损害性能,这可能是由于过度拟合造成的。 -
(3) 删除 RC(残余连接):如果没有残余连接,我们发现性能明显更差。据推测,这是因为
较低层的信息(例如,最后一个项目的嵌入和第一个块的输出)不容易传播到最后一层,并且这些信息对于提出建议非常有用,尤其是在稀疏数据集上。 -
(4)去除Dropout:我们的结果表明,
dropout可以有效地正则化模型,从而获得更好的测试性能,特别是在稀疏数据集上。结果还表明,在密集数据集上,过拟合问题不那么严重。 -
(5)-(7) 块数:毫不奇怪,零块的结果较差,因为模型只依赖于最后一项。具有一个块的变体表现相当不错,尽管使用两个块(默认模型)仍然可以提高性能,尤其是在密集数据集上,
这意味着分层的自注意力结构有助于学习更复杂的项目转换。使用三个模块可实现与默认模型相似的性能。
-(8)多头:Transformer [ 3] 的作者发现使用“多头”注意力是有用的,它把注意力应用到ℎ子空间(每个子空间都是一个 𝑑/ℎ维空间)中。然而,在我们的案例中,双头的表现始终比单头注意力略差。这可能归因于我们的问题(𝑑=512在Transformer 中)中的小𝑑,它不适合分解成更小的子空间。
4-G 训练效率和可扩展性
RQ3:SASRec的训练效率和可扩展性(关于𝑛)如何?
我们评估了模型训练效率(RQ3)的两个方面:训练速度(一个训练周期所花费的时间)和收敛时间(达到令人满意的性能所花费的时间)。我们还根据最大长度
𝑛检查了模型的可伸缩性。所有实验均使用单个 GTX-1080 Ti GPU 进行。
训练效率
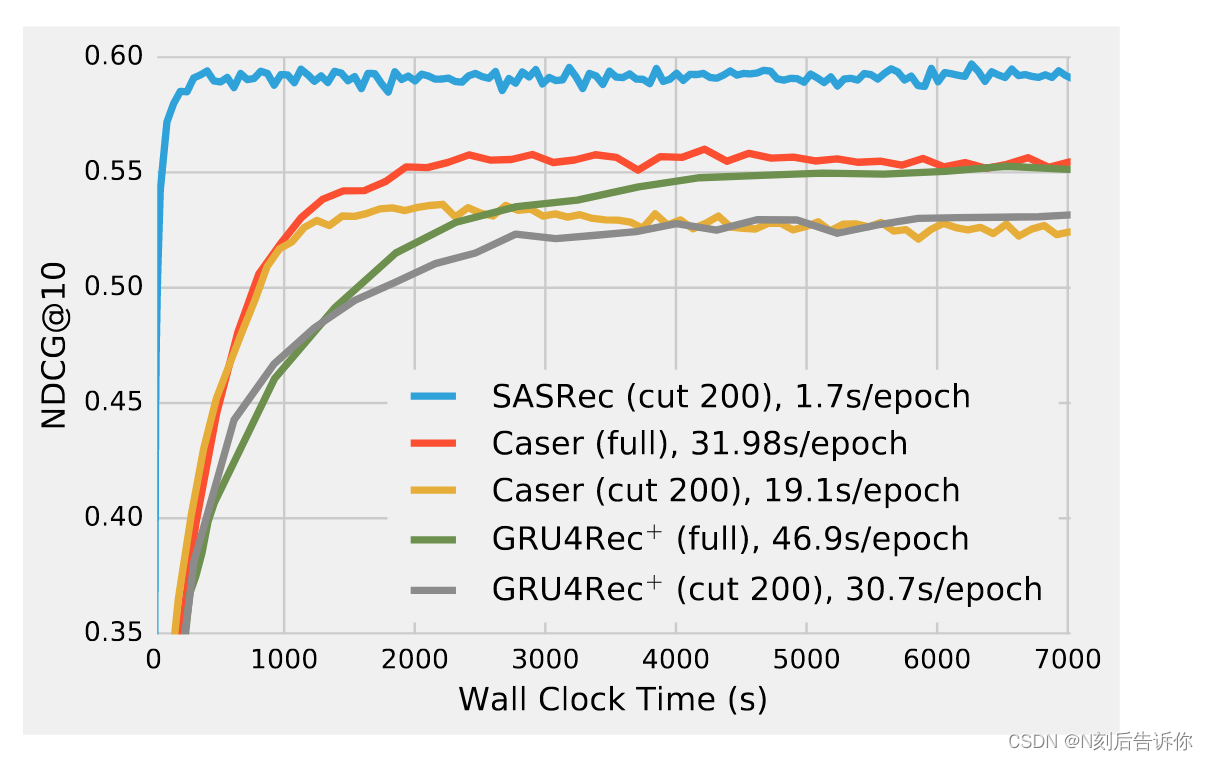
图 3 演示了基于深度学习的方法在 GPU 加速下的效率。GRU4Rec 由于性能较差而被省略。为了公平地比较,Caser 和 GRU4Rec+有两种训练选项:使用完整的训练数据或仅使用最近的 200 个动作(如 SASRec 中)。在计算速度方面,SASRec 在一个epoch内仅花费 1.7 秒进行模型更新,比 Caser(19.1 秒/周期)快 11 倍以上,比 GRU4Rec+(30.7 秒/周期)快 18 倍。我们还看到,在 ML-1M 上,SASRec 在大约 350 秒内收敛到最佳性能,而其他型号需要更长的时间。我们还发现,使用完整数据可以提高 Caser 和 GRU4Rec+的性能。
图 3:ML-1M 的训练效率。SASRec 在每个 epoch 和总训练时间方面比基于 CNN/RNN 的推荐方法快一个数量级。
可扩展性
与标准 MF 方法一样,SASRec 随用户、项目和操作的总数线性缩放。一个潜在的可扩展性问题是最大长度 𝑛,但是计算可以有效地与GPU并行化。在这里,我们用不同的𝑛方法测量了SASRec的训练时间和性能,实证研究了它的可扩展性,并分析了它在大多数情况下是否能处理顺序推荐。表 V 显示了不同序列长度下 SASRec 的性能和效率。性能越大𝑛越好,直到性能饱和(𝑛=500可能是因为 99.8% 的动作已被覆盖)。但是,即使使用𝑛=600,模型也可以在 2,000 秒内训练,这仍然比 Caser 和 GRU4Rec+快。因此,我们的模型可以很容易地扩展到多达几百个动作的用户序列,这适用于典型的审查和购买数据集。我们计划在未来研究处理超长序列的方法(在第 III-F 节中讨论)。
4-H 可视化注意力权重
注意力权重是否能够学习与位置或项目属性相关的有意义的模式?
回想一下,在时间步𝑡长中,我们模型中的自注意力机制根据它们的位置嵌入和项目嵌入自适应地为前𝑡个项目分配权重。为了回答 RQ4,我们检查了所有训练序列,并试图通过显示位置和项目的平均注意力权重来揭示有意义的模式。
位置上的注意力
图 4:不同时间步长位置的平均注意力权重的可视化。为了进行比较,基于一阶马尔可夫链的模型的热图将是一个对角矩阵。

图4显示了过去 15 个时间步长上过去15 个位置的平均注意力权重的四个热图。请注意,当我们计算平均权重时,分母是有效权重的数量,以避免在短序列中填充项目的影响。
我们考虑热图之间的一些比较:
- (a) 与 (c):这种比较表明,
该模型倾向于关注稀疏数据集 Beauty 上较新的项目,而关注密集数据集 ML-1M 上较新的项目。这是允许我们的模型自适应处理稀疏和密集数据集的关键因素,而现有方法往往集中在频谱的一端。 - (b) 与 (c):此比较显示了使用位置嵌入 (PE) 的效果。如果没有它们,注意力权重基本上均匀地分布在以前的项目上,
而默认模型 (c) 在位置上更敏感,因为它倾向于关注最近的项目。 - (c) 与 (d):由于我们的模型是分层的,这显示了不同块的注意力如何变化。显然,
高层的注意力往往集中在最近的职位上。据推测,这是因为第一个自注意力块已经考虑了之前的所有项目,而第二个块不需要考虑远处的位置。
总体而言,可视化表明,我们的自我注意力机制的行为是自适应的、位置感知的和分层的。
项之间的注意力
图 5:四个类别的电影之间的平均注意力可视化。这表明我们的模型可以发现项目的属性,并在相似的项目之间分配更大的权重。

在一些精心挑选的项目之间显示注意力权重可能在统计上没有意义。为了进行更广泛的比较,使用 MovieLens-1M,其中每部电影有几个类别,我们随机选择两个不相交的集合,每个集合包含来自 4 个类别的 200 部电影:科幻(科幻)、浪漫、动画和恐怖。第一组用于查询,第二组用作键。图 5 显示了两组之间平均注意力权重的热图。我们可以看到热图近似于一个块对角矩阵,这意味着注意力机制可以识别相似的项目(例如共享公共类别的项目),并倾向于在它们之间分配更大的权重(无需事先了解类别)。
5.结论
在这项工作中,我们提出了一种基于自我注意力的新型顺序模型SASRec,用于下一个项目推荐。SASRec 对整个用户序列进行建模(没有任何循环或卷积操作),并自适应地考虑消耗的项目进行预测。在稀疏和密集数据集上的大量实证结果表明,我们的模型优于最先进的基线,并且比基于 CNN/RNN 的方法快一个数量级。未来,我们计划通过整合丰富的上下文信息(例如停留时间、动作类型、位置、设备等)来扩展模型,并研究处理非常长的序列(例如点击)的方法。