接收简单变量的请求参数
直接使用简单变量作为形参进行接收(这里简单变量名称需要与接收的参数名称保持一致,否则需要加上@RequestParam注解):
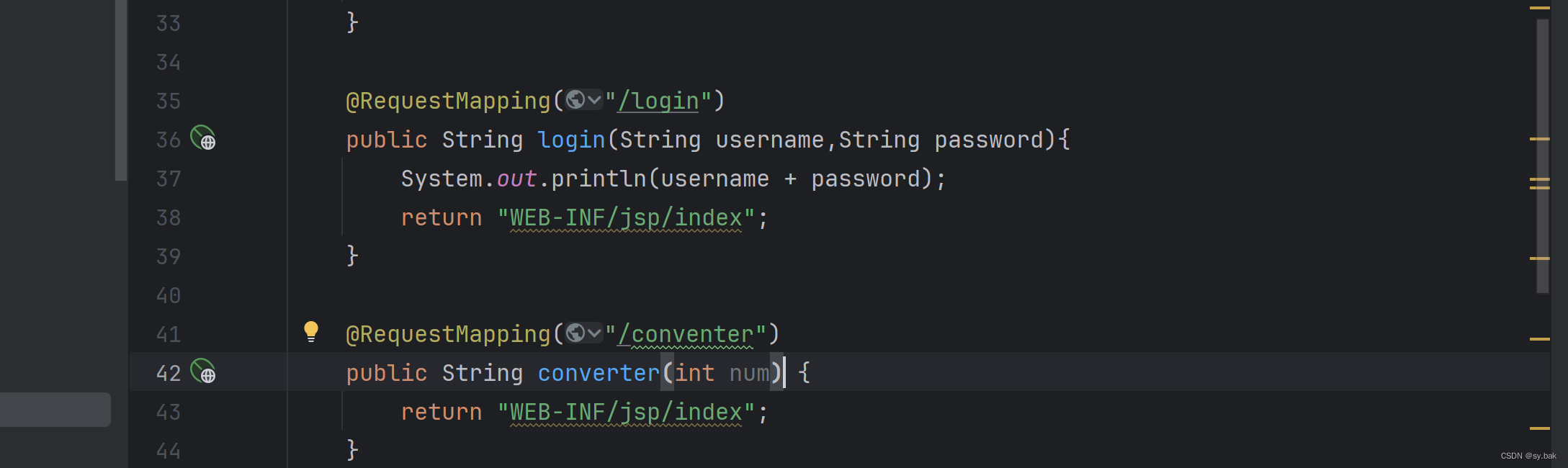
细节:
1:SpringMVC会针对常见类型(八种基本类型及其包装器,String)进行自动类型转换
2:尽量使用包装类型进行参数的接受,避免接收不到参数时报错。
接收POJO类型请求参数
什么是POJO类型?

接收方法:
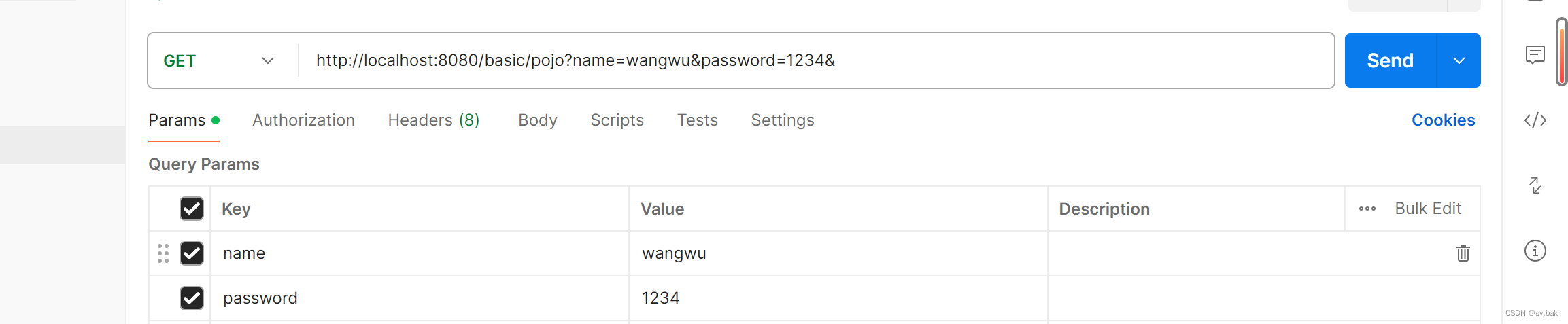
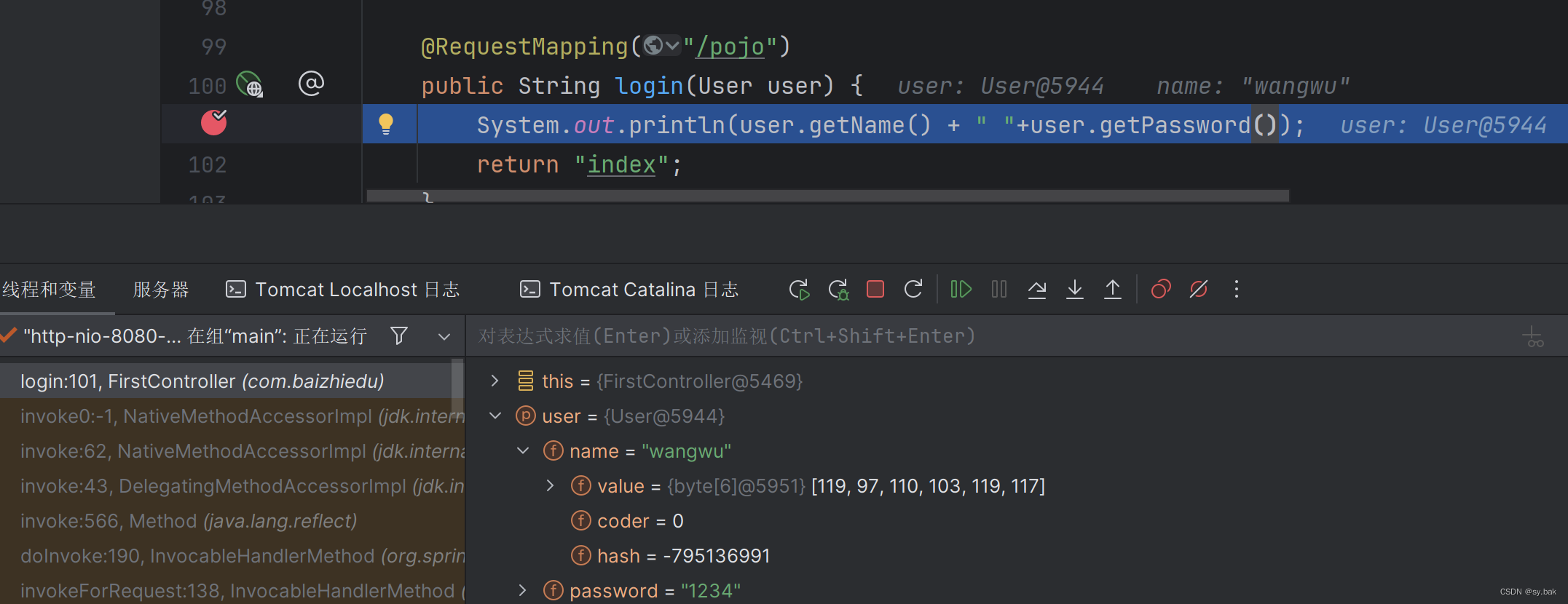
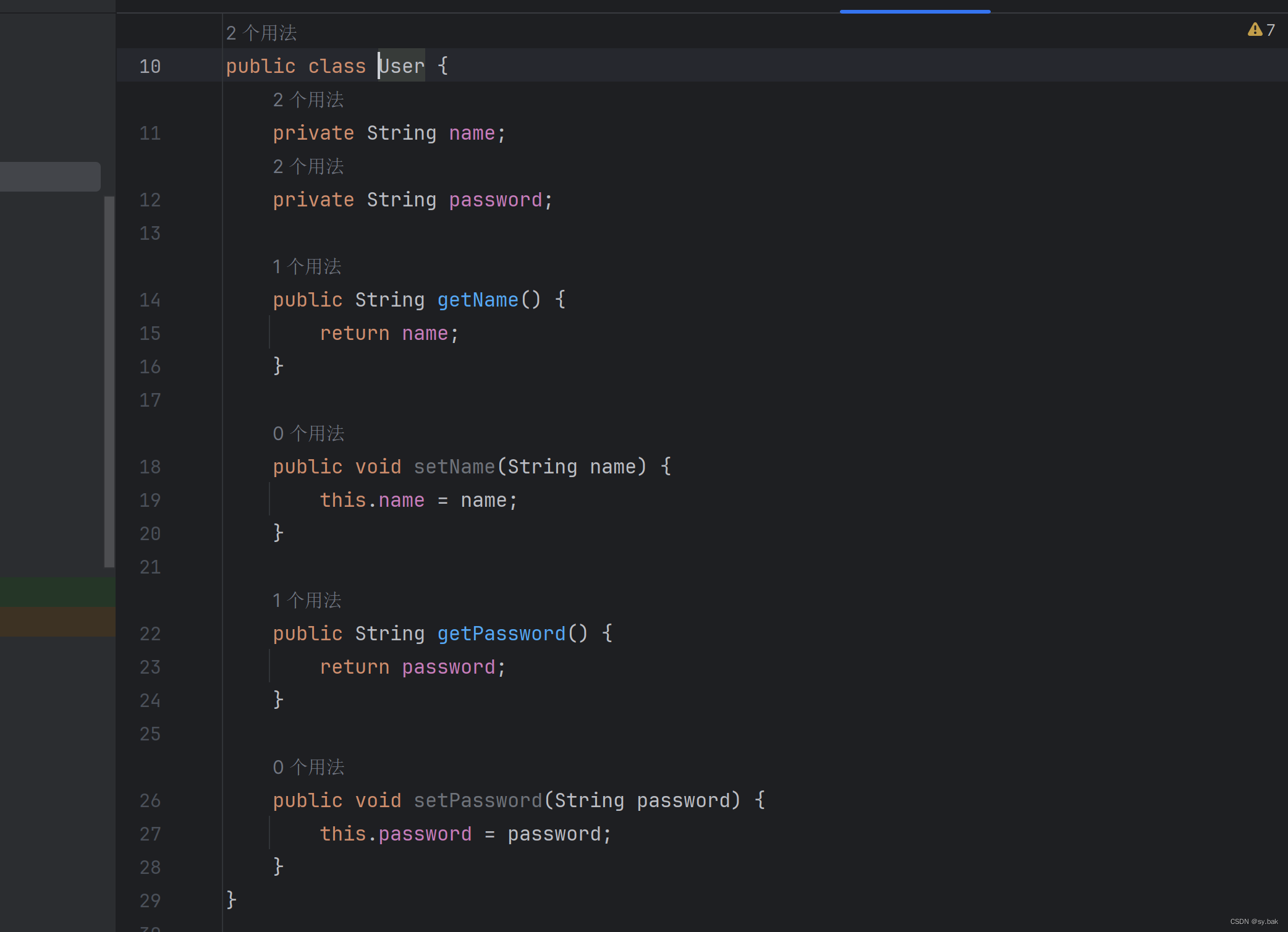
POJO接收对象时没有参数名必须与前端保持一致的要求,POJO只对对象内部有要求,POJO内部的变量必须要与接受的参数名保持一致
接收一组简单变量的请求参数
使用数组进行接收。这里遵循上述简单变量的接收规律。同样的,这里的数组名要与前端传来的参数名称保持一致。
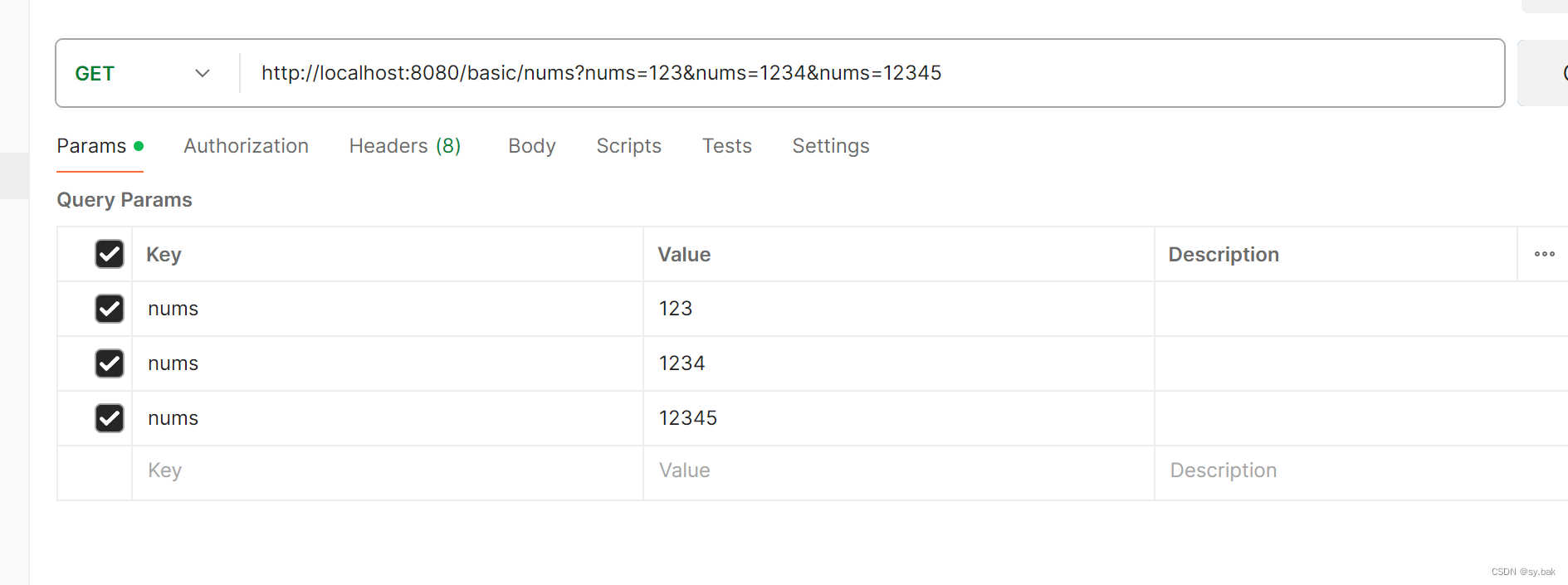
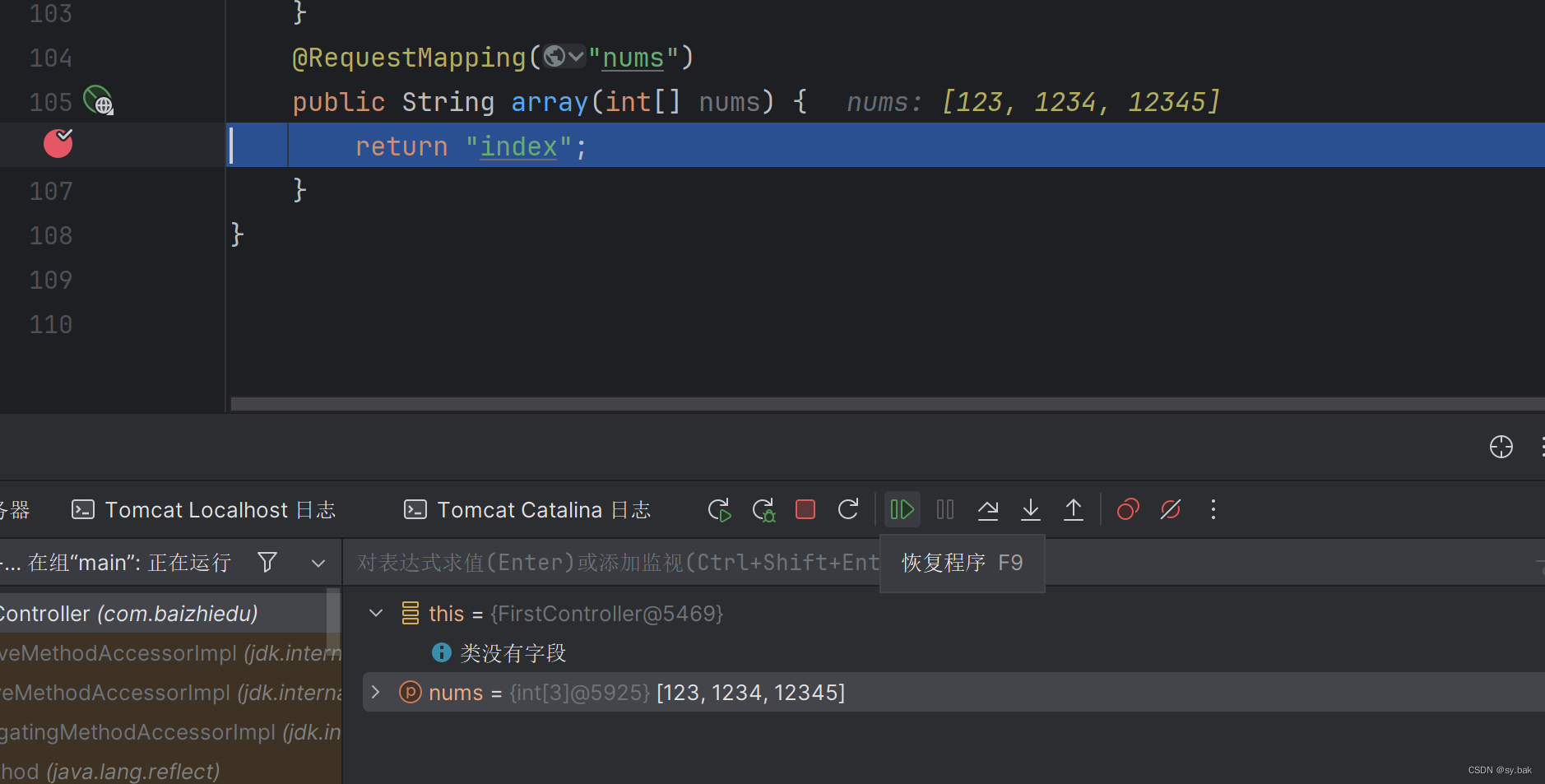
能否使用集合框架作为形参?
1:对于List这样的接口,由于没有具体的实现类所以不能作为接受请求的参数,直接回抛异常
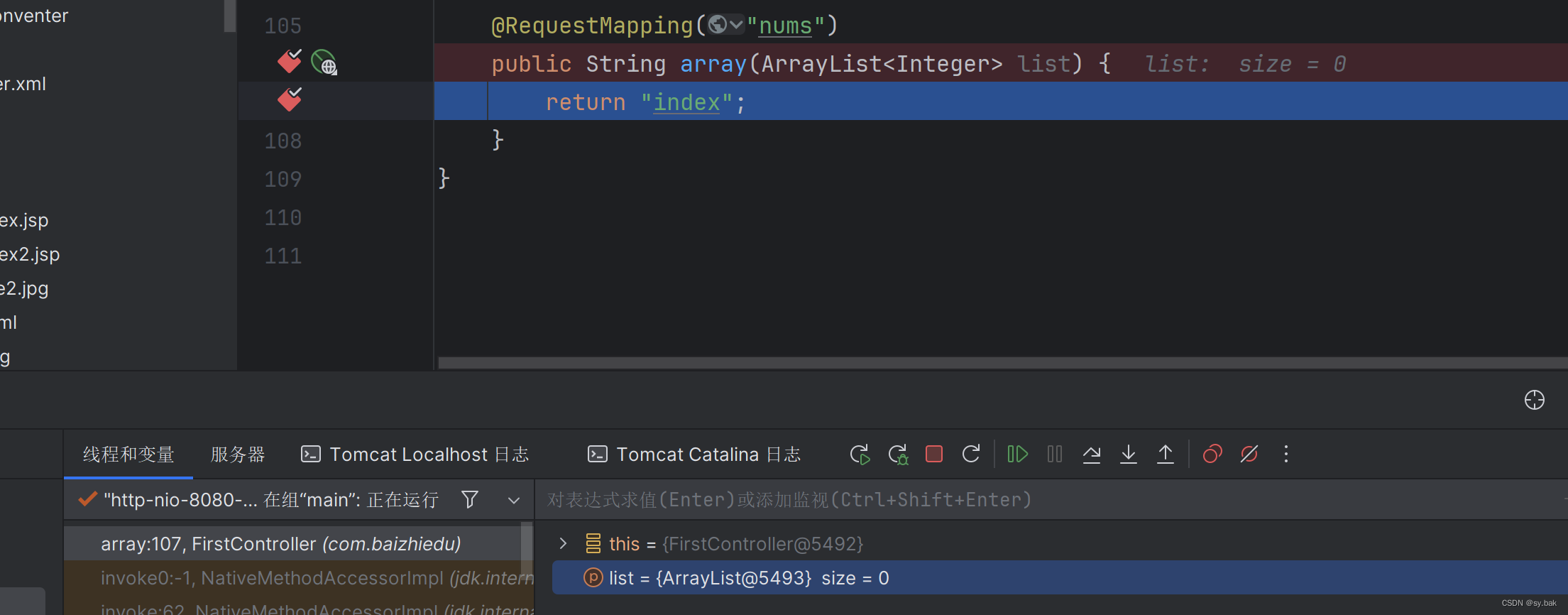
2:对于ArrayList这样的具体的实现类,类似于对象接受请求参数(pojo),spring-mvc需要通过属性名去进行参数的传递(泛型在运行时被擦除),而ArrayList是没有属性名的,所以这里ArrayList为空,拿不到任何参数。
使用List接收直接报服务器错误:
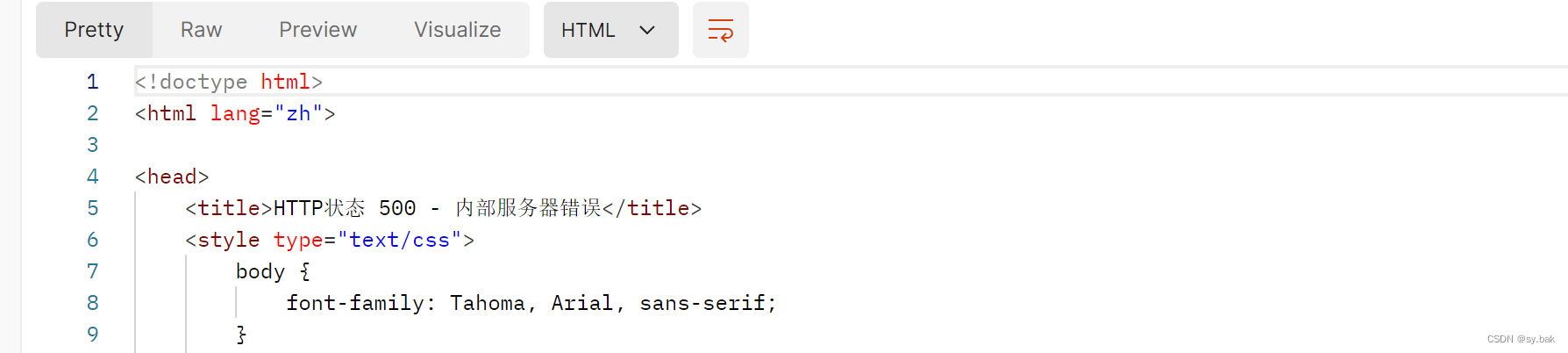
使用ArrayList没有接收到参数:
接收一组POJO类型的请求参数
自己构建一个对象,里面设置一个接收这样一组参数的对象,提供get,set方法。这里的核心是使接收这样一组参数的容器作为一个拥有get,set方法的属性。
不能使用集合框架作为形参的原因同上
自己构建一个对象,对象里面包含接收请求参数的ArrayList容器

请求构建(注意这里参数数组名称要与自己构建的对象中接收参数的容器的名称保持一致):

控制器:

接收单值动态参数
1:使用Map集合接收
2:必须使用(可变参数场景下必须使用@RequestParm注解,表示将参数映射到形参的集合中,否则形参的集合为空)
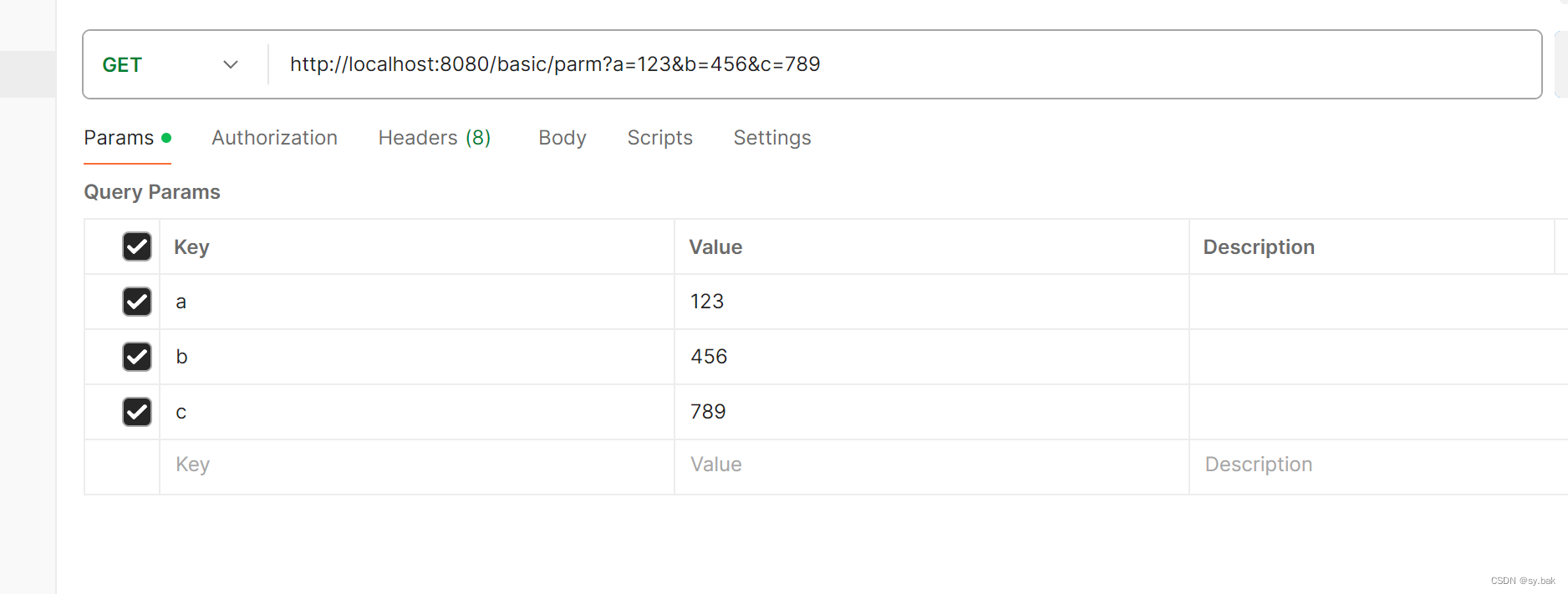
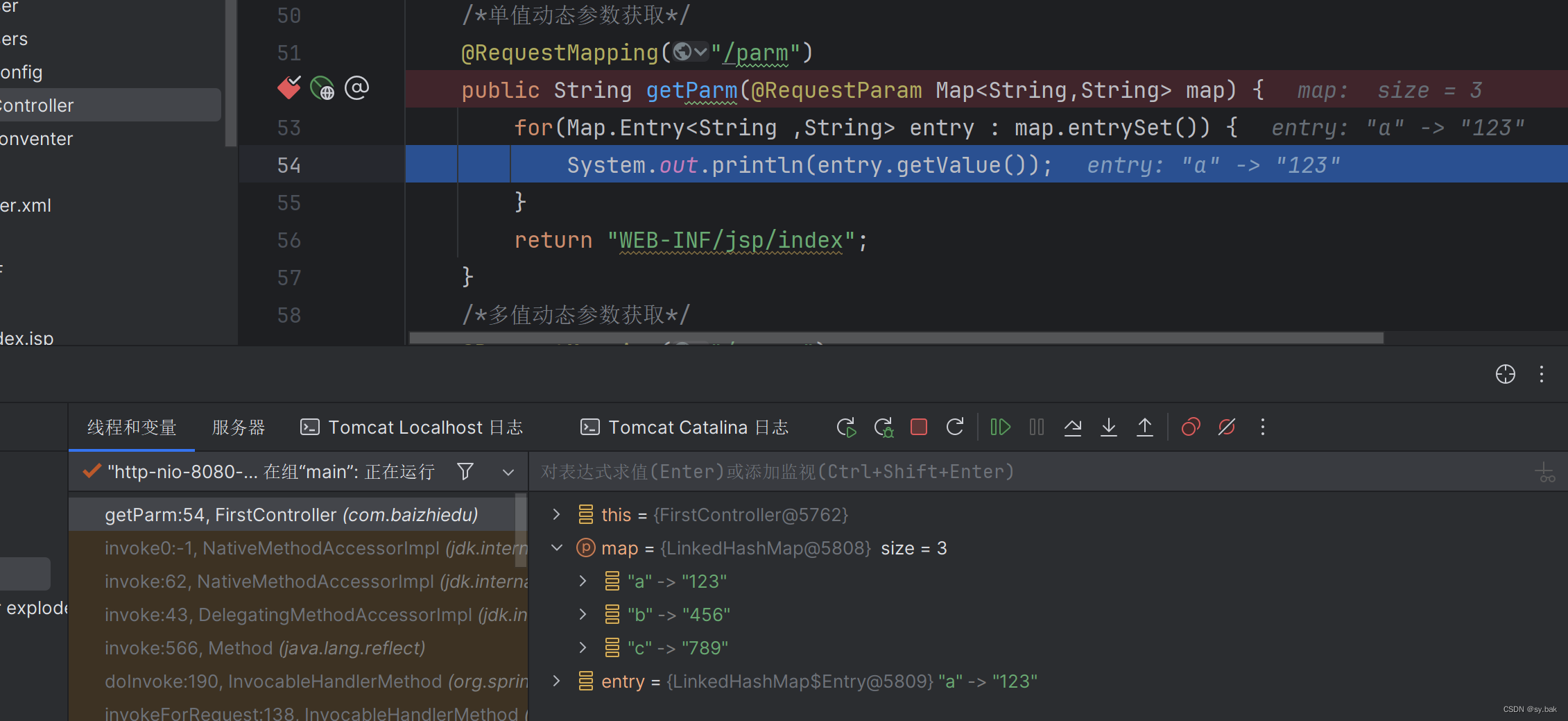
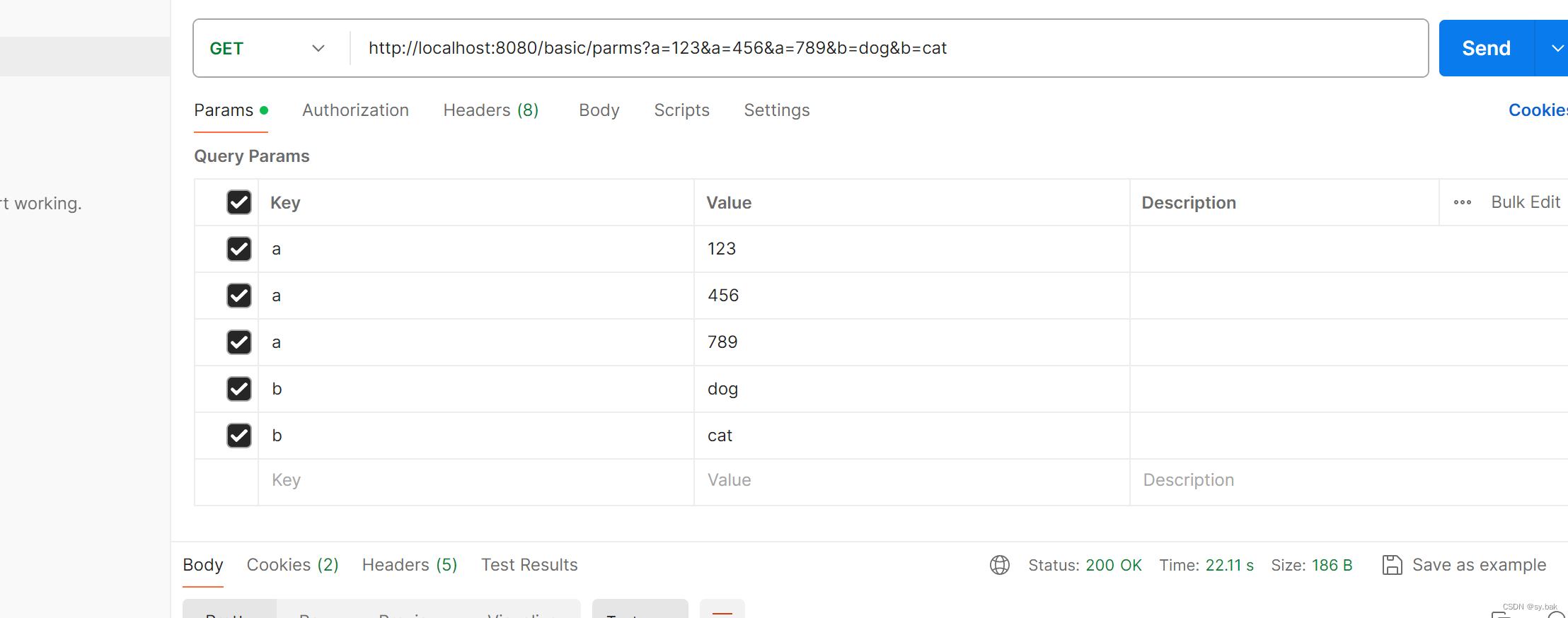
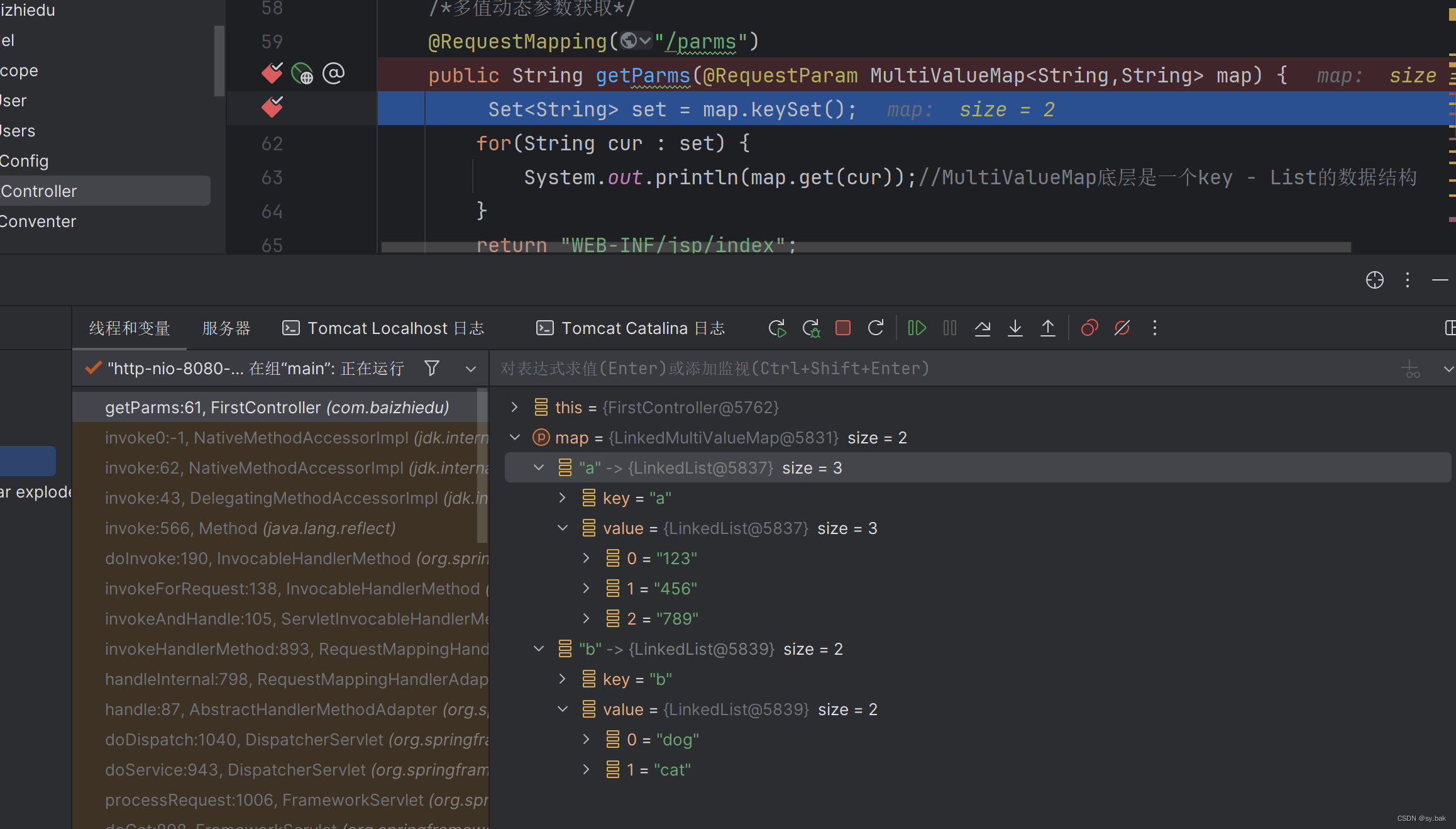
接收多值动态参数
使用MultiValueMap接收,底层是Map<K, List<V>>结构