希尔排序是对插入排序的优化,如果你不了解插入排序的话,可以先阅读这篇文章:插入排序
目录
1.插入排序的问题
2.希尔排序的思路
3.希尔排序的实现
4.希尔排序的优化
5.希尔排序的时间复杂度
1.插入排序的问题
如果用插入排序对一个逆序有序的数组排序时,时间复杂度为O(n^2),此时效率最低。
如果用插入排序对一个顺序有序的数组排序时,时间复杂度为O(n),此时效率最高。
我们发现,被排序的对象越接近有序,插入排序的效率越高,这时希尔就有了一个想法:如果可以将数组变得接近有序后再用插入排序呢?
2.希尔排序的思路
希尔排序是对插入排序的优化,它的思路是先选定一个整数作为增量,这里我们以gap(间隔)表示,将间隔为gap的数据分为一组,这样就可以分出gap组以gap为公差的等差数列的数据组。之后将这些数据组排序(把每组数据排序),之后将gap缩小,继续分组并进行排序,重复上述动作,直到gap缩小至1,此时排完了之后刚好有序。
为了让数组更接近有序的排序称为预排序,而最后一次排序是直接插入排序,而由于前面的操作使数据变得接近有序,因此最后一次直接插入排序需要移动的数据很少,效率便很高了。
下面我们来实现希尔排序。
现在我们给定如下数组,并以3为gap,可将数组根据颜色分为3组以3为公差的等差数列。
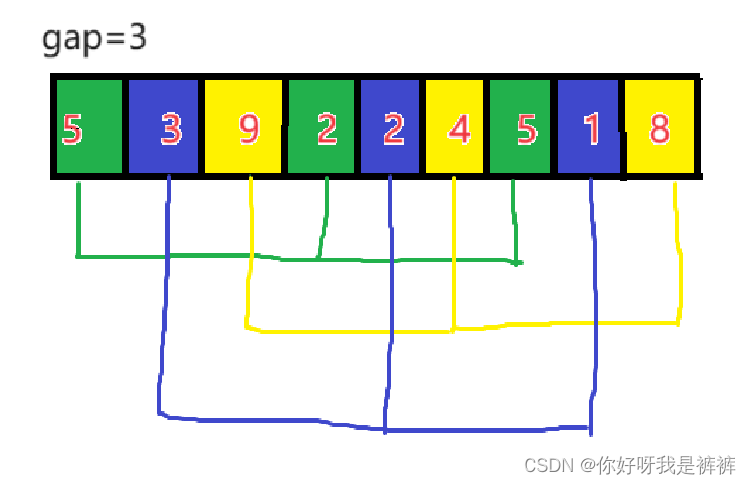
之后我们对这三组数据进行插入排序
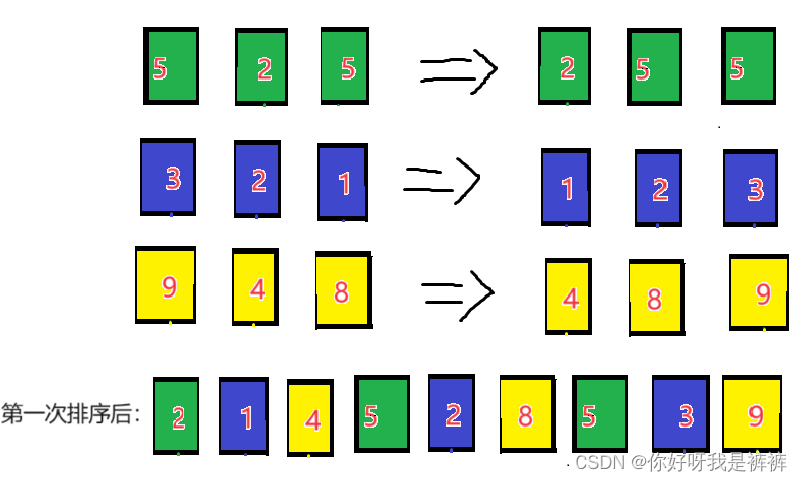
之后我们将间隔缩小, 以2为间隔,我们就可以分出两组以2为公差的等差数列。
这里也并不一定要只减少1,减少多少看我们想减少多少。

现在我们完成第二次排序

现在我们的数组已经非常接近有序,我们最后再以1为间隔,得到一组以1为间隔的等差数列,再完成最后一次排序,也就是直接插入排序,即可使得我们的数组有序。
3.希尔排序的实现
现在我们根据我们的思路来逐步实现希尔排序
第一步:以3为间隔,排序第一组绿色的

在已经学习了插入排序的基础上,我们来实现一下排序绿色
//代码中的n代表数组长度,后面的代码不再解释。
int gap = 3;
//n-gap后的数据为最后一组数据,而当i等于我们的前一组数据时
//排序的就是最后一组数据,因此结束条件为i<n-gap
for (int i = 0; i < n - gap; i += gap)
{int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;
}第二步:进行第一次排序
由于我们先前已经实现了排序绿色的,而排序蓝色的和排序黄色的不过是起始位置不同,因此我们再嵌套一层循环即可。
for (int j = 0; i < gap; j++)
{int gap = 3;//n-gap后的数据为最后一组数据,而当i等于我们的前一组数据时//排序的就是最后一组数据,因此结束条件为i<n-gapfor (int i = j; i < n - gap; i += gap){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}
}现在我们已经完成了第一次排序,那么后面的排序我们控制gap即可
for (int gap = 3; gap > 0; gap--)
{for (int j = 0; i < gap; j++){for (int i = j; i < n - gap; i += gap){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}
}这时我们发现我们的代码达到了惊人的四层循环...这段代码未免有些过于恐怖...
那我们有没有什么办法优化这段代码呢?
4.希尔排序的优化
这时有一位大佬给出了这么一个解决方法:
我们不再一次比较一个数据组,
而是先比较第一个数据组的第一个数据和第二个数据,
然后比较第二个数据组的第一个数据和第二个数据,
之后比较第三个数据组的第一个数据和第二个数据,
然后比较第二个数据组的第二个数据和第三个数据,
这么一直比较下去,就可以完成我们第一次预排序的效果。
如下图所示,相同颜色的线表示比较的数据。

代码如下所示:
int gap = 3
for (int i = 0; i < n - gap; i++)
{int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;
}现在我们已经完成了第一趟的排序,接下来我们控制gap即可。
int gap = 3;
while (gap > 0)
{for (int i = 0; i < n - gap; i++){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}gap--;
}现在这段代码看起来就舒服多了。但是我们的gap就一定每次都减1吗?
我们之前说过,预排序是为了让数组更加有序,我们只要能够让数组更加有序就可以了,没有必要每次让gap减1,gap太大了反而会有一些副作用。
这时有一位大佬写了这么一个希尔排序:
int gap = n;
while (gap > 0)
{gap /= 2;for (int i = 0; i < n - gap; i++){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}
}这里的第一趟循环以二分之数组长度为间隔,后续的循环每次都除以2。
到了最后一次循环之时,gap要么等于2,要么等于3;而它们除2都等于1。这样就保证了最后一次循环是直接插入排序,可谓是相当完美了。
现在我们将其封装在函数体内,完成最终版的希尔排序
void InsertSort(int* a, int n)
{int gap = n;while (gap > 0){gap /= 2;for (int i = 0; i < n - gap; i++){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}
}5.希尔排序的时间复杂度
我们发现我们最终版的希尔排序也拥有三层循环,于是乎我们大家就对希尔排序的效率产生了疑问.但是利用我们现有数学能力无法计算出希尔排序的时间复杂度,只能给出一个大致范围
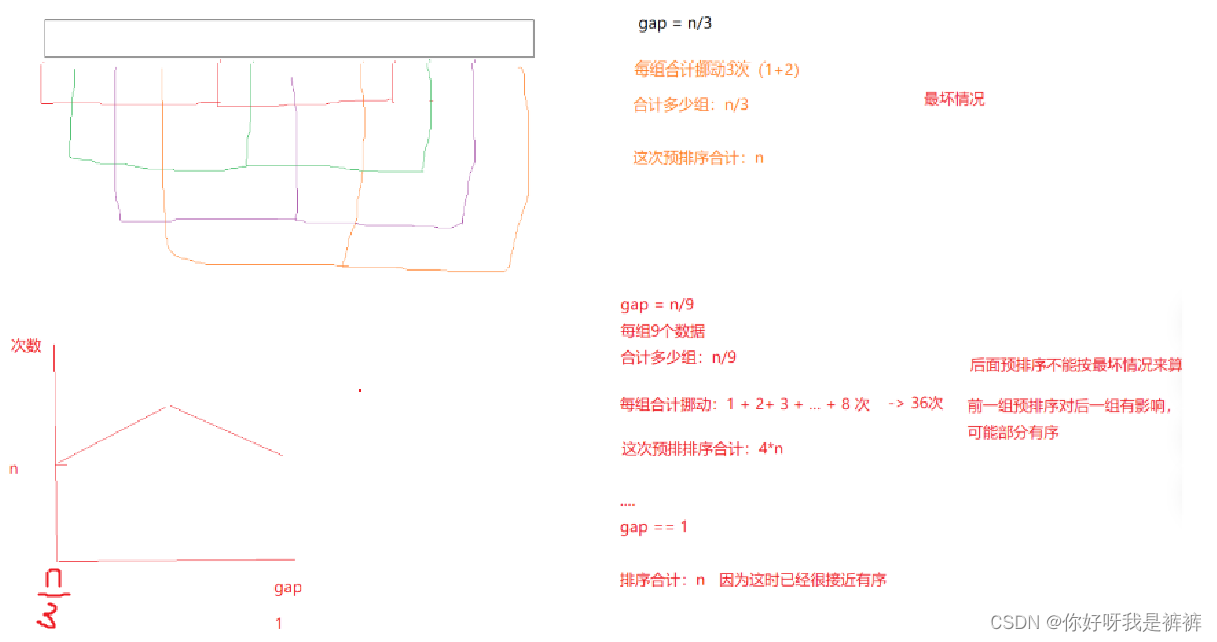
下面给出严蔚敏教授数据结构书中的相关论述:

在这里也可以给大家大概画一下图,由于每次排序都会对后续的排序产生影响,因此我们后续的排序移动的数据会越来越少,因此效率还是比较高的。


![[国产大模型简单使用介绍] 开源与免费API](https://img-blog.csdnimg.cn/img_convert/aeb7b16093020e4c1a37aef8e8ef5b97.png)



![[保姆式教程]使用目标检测模型YOLO V8 OBB进行旋转目标的检测:训练自己的数据集(基于卫星和无人机的农业大棚数据集)](https://img-blog.csdnimg.cn/direct/9df1d9d27d744a4c899f91b5e1b573ff.jpeg)