283. 移动零

283. 移动零 - 力扣（LeetCode）

数据划分、数据分块
利用数组下标充当指针
cur：从左往右扫描数组，遍历数组
dest：已处理的区间内，非零元素的最后一个位置
一共被分为三个区间
[0,dest] [dest+1,cur-1] [cur,n-1]
   非0              0             待处理  
输入：nums[0,1,0,3,12]
[1,0,0,3,12]
[1,0,0,3,12]
[1,3,0,0,12]
[1,3,12,0,0]
输出：nums[1,3,12,0,0]

cur从前往后遍历的过程中：
1. 遇到0元素：cur++;
2. 遇到非0元素：dest+1然后交换
swap(dest+1,cur);
dest++,cur++;
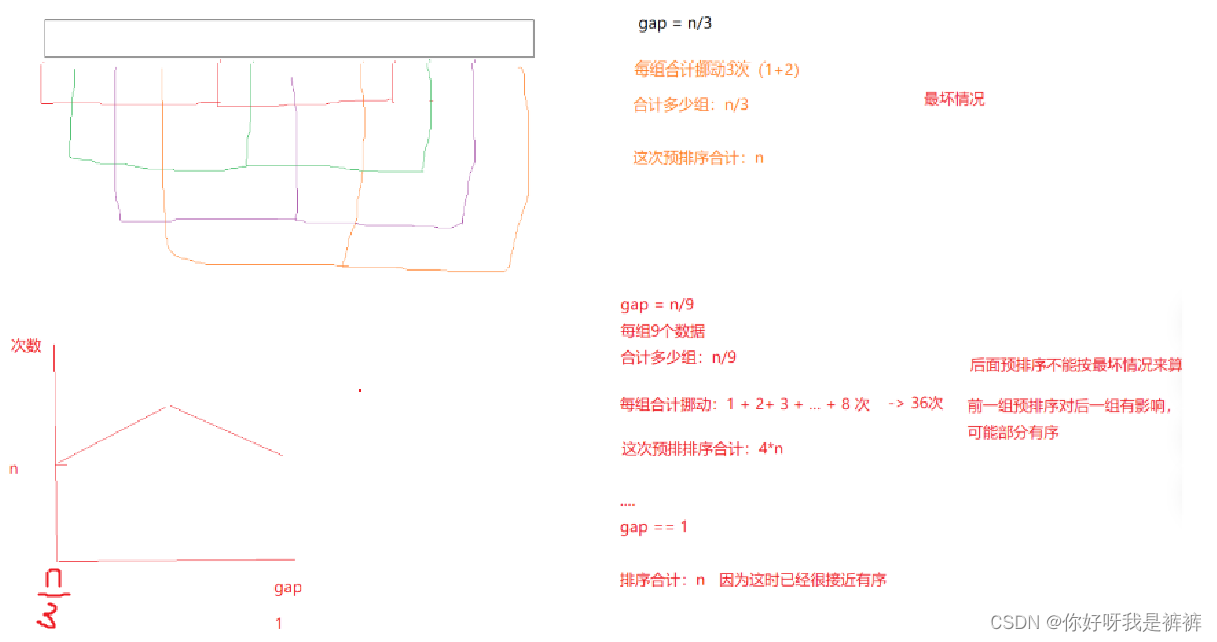
双指针是快速排序里面最核心的一步

代码：C++

class Solution {
public:void moveZeroes(vector<int>& nums) {for(int cur = 0, dest = -1; cur < nums.size(); cur++){if(nums[cur]) // nums[cur] != 0{swap(nums[++dest], nums[cur]);}}}
};

1089. 复写零

1089. 复写零 - 力扣（LeetCode）

输入：arr = [1,0,2,3,0,4,5,0]
输出：[1,0,0,2,3,0,0,4]
解释：调用函数后，输入的数组将被修改为：[1,0,0,2,3,0,0,4]

解法：双指针算法

先根据“异地”操作，然后优化成双指针下的“就地”操作
1. 先找到最后一个“复写”的数；
双指针算法
a.先判断cur位置的值
b.决定dest向后移动一步后者两步
c.判断dest是否已经到结束为止
4.cur++

2. 处理一下边界情况，如果出现cur指向0但是dest+=2之后出现越界情况的话（dest指向数组外）
n-1位置的值修改成0，让cur--，让dest-=2

3. 从后向前完成复写操作

代码：C++

class Solution 
{
public:void duplicateZeros(vector<int>& arr) {// 时间: O(n)// 空间: O(1)//1. 先找到最后一个数int cur = 0, dest = -1, n = arr.size();while(cur < n){if(arr[cur]) dest++;else dest += 2;if(dest >= n - 1) break;//dest有可能跑到n的位置，所以如果>=n了，就表明cur指向的已经是要复写的数cur++;}//2. 处理一下边界情况if(dest == n){arr[n - 1] = 0;cur--; dest -= 2;}//3. 从后向前完成复写操作while(cur >= 0){if(arr[cur]) arr[dest--] = arr[cur--];else{arr[dest--] = 0;arr[dest--] = 0; //0覆盖两次cur--;}}}
};

202. 快乐数

202. 快乐数 - 力扣（LeetCode）

 

可以抽象成：判断链表是否有环
解法：快慢双指针
1. 定义快慢指针

2. 慢指针每次向后移动一步，快指针每次向后移动两步

3. 判断相遇时候的值即可

最大当的范围就是：2.1 * 10^9 比如9999999999，一共十位数
9^2 * 10 = 810
所以是从1到810之间变化，所以一定会成环

代码：C++

class Solution {
public:int bitSum(int n) // 返回n这个数每一位上的平方和{int sum = 0;while(n){int t = n % 10; // 最低位sum += t * t;n /= 10; // 把最低位干掉}return sum;}bool isHappy(int n) {int slow = n, fast = bitSum(n);while(slow != fast){slow = bitSum(slow); // slow走一步fast = bitSum(bitSum(fast)); // fast走两步}return slow == 1;}
};