近临算法（个人总结版）

背景

近邻算法（Nearest Neighbor Algorithm）是一种基本但非常有效的分类和回归方法。最早由Fix和Hodges在1951年提出，经过几十年的发展和改进，已成为数据挖掘、模式识别和机器学习领域的重要工具。近邻算法基于相似性原则，通过查找最接近的样本进行预测。其核心思想是相似的样本具有相似的特征，因而在预测时可以参考相似样本的类别或数值。常见的近邻算法包括k近邻算法（k-Nearest Neighbors, k-NN）、KD树（KD-Tree）和球树（Ball Tree）。

一、近邻算法的基本概念

近邻算法通过比较样本之间的距离来进行分类或回归。其核心思想是相似的样本具有相似的特征，因而在预测时可以参考相似样本的类别或数值。

1.1 距离度量

常用的距离度量包括：

  • 欧氏距离（Euclidean Distance）：最常用的距离度量，适用于连续型数据。公式为：

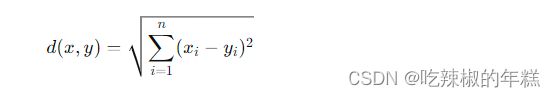
  • 曼哈顿距离（Manhattan Distance）：适用于高维空间和稀疏数据。公式为：

  • 闵可夫斯基距离（Minkowski Distance）：欧氏距离和曼哈顿距离的推广，适用于多种情况。公式为：

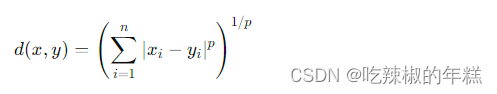
  • 余弦相似度（Cosine Similarity）：用于度量两个向量之间的夹角，相似度越大，距离越小。公式为：

1.2 算法类型

  • 分类：将新样本分类到与其最相似的样本所属的类别。
  • 回归：预测新样本的数值为与其最相似的样本数值的加权平均。

二、k近邻算法（k-NN）

2.1 基本原理

k近邻算法通过查找与目标样本最近的k个样本进行预测。对于分类任务，k个邻居中的多数类作为预测结果；对于回归任务，k个邻居的平均值作为预测结果。k近邻算法无需训练过程，直接利用所有训练数据进行预测，因此也被称为懒惰学习算法（Lazy Learning）。

2.2 具体实现

以下是k近邻算法的分类实现：

import numpy as np
from collections import Counter
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_scoreclass KNN:def __init__(self, k=3):self.k = kdef fit(self, X, y):self.X_train = Xself.y_train = ydef predict(self, X):predictions = [self._predict(x) for x in X]return np.array(predictions)def _predict(self, x):distances = [np.sqrt(np.sum((x - x_train)**2)) for x_train in self.X_train]k_indices = np.argsort(distances)[:self.k]k_nearest_labels = [self.y_train[i] for i in k_indices]most_common = Counter(k_nearest_labels).most_common(1)return most_common[0][0]# 加载示例数据集
iris = load_iris()
X, y = iris.data, iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 训练和预测
knn = KNN(k=3)
knn.fit(X_train, y_train)
predictions = knn.predict(X_test)# 计算准确率
print("Accuracy:", accuracy_score(y_test, predictions))

2.3 优劣势

优势：

  • 简单易懂：k近邻算法的基本思想简单直观，易于理解和实现。
  • 无训练过程：无需训练过程，直接利用所有训练数据进行预测。

劣势：

  • 计算复杂度高：对每个测试样本都需要计算与所有训练样本的距离，因此预测过程的计算复杂度较高，适合小规模数据集。
  • 对噪声数据敏感：k近邻算法对噪声数据较为敏感，可能影响预测结果。
  • 数据标准化要求：不同特征的量纲不同时，需对数据进行标准化处理，否则距离计算可能会受到影响。

三、KD树（KD-Tree）

3.1 基本原理

KD树是一种对k近邻算法进行优化的数据结构，通过将数据划分到k维空间中的子区域，实现高效的最近邻搜索。KD树通过递归地将数据空间划分为k维超矩形，适用于低维数据的最近邻搜索。

3.2 具体实现

以下是KD树的实现和最近邻搜索：

from scipy.spatial import KDTree# 示例数据
X = np.random.rand(10, 2)# 构建KD树
kd_tree = KDTree(X)# 查询最近邻
point = np.random.rand(1, 2)
distance, index = kd_tree.query(point)print("Nearest neighbor:", X[index])
print("Distance:", distance)

3.3 优劣势

优势：

  • 提高了k近邻搜索的效率：KD树通过分割数据空间，实现了快速的最近邻搜索，特别适合低维数据。
  • 支持动态插入和删除操作：KD树允许动态插入和删除数据点，适用于数据集动态变化的场景。

劣势：

  • 构建和维护树结构的复杂度较高：构建KD树需要较高的计算复杂度，插入和删除操作也较为复杂。
  • 维度灾难：随着维度增加，KD树的性能提升有限，高维数据的最近邻搜索效果不佳。

四、球树（Ball Tree）

4.1 基本原理

球树是一种替代KD树的结构，通过使用超球体代替超矩形来划分空间，适用于高维数据和度量空间。球树通过递归地将数据空间划分为球形区域，实现高效的最近邻搜索。

4.2 具体实现

以下是球树的实现和最近邻搜索：

from sklearn.neighbors import BallTree# 示例数据
X = np.random.rand(10, 2)# 构建球树
ball_tree = BallTree(X)# 查询最近邻
point = np.random.rand(1, 2)
dist, ind = ball_tree.query(point)print("Nearest neighbor:", X[ind])
print("Distance:", dist)

4.3 优劣势

优势：

  • 适用于高维数据：球树在高维空间中表现良好，比KD树更适合高维数据。
  • 支持多种距离度量：球树支持多种距离度量，如欧氏距离、曼哈顿距离等。

劣势：

  • 构建和维护树结构的复杂度较高：构建和维护球树需要较高的计算复杂度，插入和删除操作也较为复杂。
  • 构建时间较长：随着数据规模增加，构建球树的时间较长。

五、应用实例

5.1 手写数字识别

使用k-NN算法进行手写数字识别：

from sklearn.datasets import load_digits
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.neighbors import KNeighborsClassifier# 加载数据
digits = load_digits()
X, y = digits.data, digits.target# 预处理数据
scaler = StandardScaler()
X = scaler.fit_transform(X)# 分割数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 训练k-NN分类器
knn = KNeighborsClassifier(n_neighbors=3)
knn.fit(X_train, y_train)# 预测并计算准确率
predictions = knn.predict(X_test)
print("Accuracy:", accuracy_score(y_test, predictions))

5.2 图像检索

使用KD树进行图像特征的最近邻搜索：

from sklearn.decomposition import PCA
from sklearn.datasets import fetch_olivetti_faces
from scipy.spatial import KDTree# 加载数据
faces = fetch_olivetti_faces()
X, y = faces.data, faces.target# 降维
pca = PCA(n_components=50)
X_pca = pca.fit_transform(X)# 构建KD树
kd_tree = KDTree(X_pca)# 查询最近邻
query_image = X_pca[0].reshape(1, -1)
dist, ind = kd_tree.query(query_image, k=5)# 输出最近邻结果
print("Nearest neighbors:", ind)
print("Distances:", dist)

5.3 文章推荐

使用球树进行文章推荐：

from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.neighbors import BallTree# 示例文章
documents = ["The quick brown fox jumps over the lazy dog.","Never jump over the lazy dog quickly.","Bright vixens jump; dozy fowl quack.","Jinxed wizards pluck ivy from the big quilt.","The five boxing wizards jump quickly."
]# 计算TF-IDF特征
vectorizer = TfidfVectorizer()
X = vectorizer.fit_transform(documents).toarray()# 构建球树
ball_tree = BallTree(X, metric='cosine')# 查询最近邻
query = vectorizer.transform(["Jumping over dogs is fun."]).toarray()
dist, ind = ball_tree.query(query, k=3)# 输出最近邻结果
print("Nearest neighbors:", ind)
print("Distances:", dist)

六、总结

近邻算法是一类基础且强大的分类和回归方法，广泛应用于图像识别、推荐系统等领域。本文详细介绍了k近邻算法（k-NN）、KD树（KD-Tree）、球树（Ball Tree）的基本原理、具体实现、优劣势及应用实例。通过这些算法的学习和应用，可以有效提高分类和回归任务的性能和精度。

拓展阅读与参考文献

  1. 《统计学习方法》 - 李航
  2. 《机器学习》 - 周志华
  3. 《模式分类》 - Duda, Hart, Stork
  4. Efficient Algorithms for Nearest Neighbor Search in High Dimensions - Arya, Mount, Netanyahu, Silverman, Wu (1998)
  5. Nearest Neighbors in High-Dimensional Data: The Efficiency-Accuracy Tradeoff - Indyk, Motwani (1998)

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/331249.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

vue源码2

vue源码2

vue之mustache库的机理其实是将模板字符串转化为tokens 然后再将 tokens 转化为 dom字符串&#xff0c;如下图 对于一般的将模板字符串转化为dom字符串&#xff0c;这样不能实现复杂的功能 let data {name:小王,age:18 } let templateStr <h1>我叫{{name}},我今年{{ag…
阅读更多...
git分支常用命令

git分支常用命令

最近在用git提交代码的时候&#xff0c;发现有些命令不是很会&#xff0c;先记录几个常用分支命令&#xff0c;后续再补充&#xff0c;在执行git push命令提交代码的时候遇到报错&#xff0c;一并记录下。 1.git常用命令 新建分支&#xff1a; git branch <分支名称> 比…
阅读更多...
2025第十届美陈展

2025第十届美陈展

展位又遭疯抢&#xff01;2025第十届美陈展释放“无界之美” 美是全球通用的语言&#xff0c;人类对美的追求始终如一&#xff0c;大众审美在经历了时代的变迁后开始趋同&#xff0c;东方文明深处的美学经济开始崛起。 在如今商业迈入存量阶段&#xff0c;以品牌为突破口打造…
阅读更多...
Ai自动贴图直播项目的趋势，智享自动直播GMV增加工具

Ai自动贴图直播项目的趋势，智享自动直播GMV增加工具

在当今社会&#xff0c;直播行业正在悄然地改变着人们的生活方式。无论是在闲暇时光中放松身心&#xff0c;还是在临睡前享受休闲娱乐&#xff0c;观众们越来越习惯于通过刷短视频或者观看直播来消遣自己。根据统计数据显示&#xff0c;到2023年全球将有超过10.74亿网民&#x…
阅读更多...
前端日志收集（monitor-report v1）

前端日志收集（monitor-report v1）

为什么 为什么自己封装而不是使用三方 类似 Sentry 这种比较全面的 因为 Sentry 很大我没安装成功&#xff0c;所有才自己去封装的 为什么使用 可以帮助你简单解决前端收集错误日志、收集当前页面访问量&#xff0c;网站日活跃&#xff0c;页面访问次数&#xff0c;用户行…
阅读更多...
海外仓储管理系统：提升效率，标准化海外仓管理，科技赋能业务

海外仓储管理系统：提升效率，标准化海外仓管理，科技赋能业务

海外仓作为跨境物流的关键一环&#xff0c;完全可以说海外仓的效率直接决定了后续物流的整体运作效率。 对于海外仓而言&#xff0c;一套高效&#xff0c;易用的海外仓储系统&#xff0c;无疑将成为提升企业竞争力的重要工具&#xff0c;帮助海外仓实现从野蛮生长到标准化管理…
阅读更多...
pytorch-13_2 模型结构选择策略：层数、激活函数、神经元个数

pytorch-13_2 模型结构选择策略：层数、激活函数、神经元个数

一、拟合度概念 在所有的模型优化问题中&#xff0c;最基础的也是最核心的问题&#xff0c;就是关于模型拟合程度的探讨与优化。根据此前的讨论&#xff0c;模型如果能很好的捕捉总体规律&#xff0c;就能够有较好的未知数据的预测效果。但限制模型捕捉总体规律的原因主要有两点…
阅读更多...
02_前端三大件HTML

02_前端三大件HTML

文章目录 HTML用于网页结构搭建1. 标签2. 客户端服务器交互流程3. 专业词汇4. html语法细节5. 安装VSCODE安装插件6. Live Server插件使用7. 标题&段落&换行&列表8. 超链接标签使用9. 图片10. 表格的写法11. 表单标签*(重点)12. 下拉框13. 页面布局标签14. 块元素和…
阅读更多...
java —— 封装、继承、接口和多态

java —— 封装、继承、接口和多态

一、封装 封装是将数据和操作这些数据的方法整合成一个类。在这个类中&#xff0c;用 private 修饰符将某些数据隐藏起来&#xff0c;只通过特定的方法实现这些数据的访问和修改&#xff0c;以此实现数据的完整和安全性。 封装的步骤&#xff1a; 二、继承 继承是指把子类共有…
阅读更多...
韵搜坊 -- Elastic Stack快速入门

韵搜坊 -- Elastic Stack快速入门

文章目录 现有问题Elastic Stack介绍&#xff08;一套技术栈&#xff09;安装ES安装KibanaElasticsearch概念倒排索引Mapping分词器IK分词器&#xff08;ES插件&#xff09;打分机制 ES的几种调用方式restful api调用&#xff08;http 请求&#xff09;kibana devtools客户端调…
阅读更多...
Creating Server TCP listening socket *:6379: listen: Unknown error

Creating Server TCP listening socket *:6379: listen: Unknown error

错误&#xff1a; 解决方法&#xff1a; 在redis安装路径中打开cmd命令行窗口&#xff0c;输入 E:\Redis-x64-3.2.100>redis-server ./redis.windows.conf结果&#xff1a;
阅读更多...
Jenkins 构建 Web 项目：构建服务器和部署服务器分离的情况

Jenkins 构建 Web 项目：构建服务器和部署服务器分离的情况

构建命令 #!/bin/bash node -v pnpm -v pnpm install pnpm build:prod # 将dist打包成dist.zip zip -r dist.zip dist
阅读更多...
微软密谋超级AI大模型！LangChain带你轻松玩转大模型开发

微软密谋超级AI大模型！LangChain带你轻松玩转大模型开发

此前&#xff0c;据相关媒体报道&#xff0c;微软正在研发一款名为MAI-1的最新AI大模型&#xff0c;其参数规模或将达5000亿以上&#xff0c;远超此前微软推出的相关开源模型&#xff0c;其性能或能与谷歌的Gemini 1.5、Anthropic的Claude 3和OpenAI的GPT-4等知名大模型相匹敌。…
阅读更多...
Android 自定义图片进度条

Android 自定义图片进度条

用系统的Progressbar&#xff0c;设置图片drawable作为进度条会出现图片长度不好控制&#xff0c;容易被截断&#xff0c;或者变形的问题。而我有个需求&#xff0c;使用图片背景&#xff0c;和图片进度&#xff0c;而且在进度条头部有个闪光点效果。 如下图&#xff1a; 找了…
阅读更多...
深入探索：移动云服务器的强大之处

深入探索：移动云服务器的强大之处

文章目录 一 什么是移动云二 移动云服务器的使用三 移动云服务器的优点四 在移动云上部署node.js项目五 移动云服务器的应用场景六 移动云服务器的使用体验总结 一 什么是移动云 移动云是指用户可以通过移动设备访问云端的数据和应用&#xff0c;无需在本地设备上进行存储和处…
阅读更多...
并发编程笔记7--并发编程基础

并发编程笔记7--并发编程基础

1、线程简介 1.1、什么是线程 现代操作系统中运行一个程序&#xff0c;会为他创建一个进程。而每一个进程中又可以创建许多个线程。现代操作系统中线程是最小的调度单元。 两者关系&#xff1a;一个线程只属于一个进程&#xff0c;而一个进程可以拥有多个线程。线程是一个轻量…
阅读更多...
SQL面试题练习 —— 计算次日留存率

SQL面试题练习 —— 计算次日留存率

题目 现有用户登录记录表&#xff0c;已经按照用户日期进行去重处理。以用户登录的最早日期作为新增日期&#xff0c;请计算次日留存率是多少。 样例数据 ----------------------- | user_id | login_date | ----------------------- | aaa | 2023-12-01 | | bbb …
阅读更多...
ATmega328P加硬件看门狗MAX824L看门狗

ATmega328P加硬件看门狗MAX824L看门狗

void Reversewdt(){ //硬件喂狗&#xff0c;11PIN接MAX824L芯片WDIif (digitalRead(11) HIGH) {digitalWrite(11, LOW); //低电平} else {digitalWrite(11, HIGH); //高电平 }loop增加喂狗调用 void loop() { …… Reversewdt();//喂狗 }
阅读更多...
【活动】开源与闭源大模型：探索未来趋势的双轨道路

【活动】开源与闭源大模型：探索未来趋势的双轨道路

&#x1f308;个人主页: 鑫宝Code &#x1f525;热门专栏: 闲话杂谈&#xff5c; 炫酷HTML | JavaScript基础 ​&#x1f4ab;个人格言: "如无必要&#xff0c;勿增实体" 文章目录 开源与闭源大模型&#xff1a;探索未来趋势的双轨道路引言一、开源大模型&#…
阅读更多...
设计模式使用（成本扣除）

设计模式使用（成本扣除）

前言 名词解释 基础名词 订单金额&#xff1a;用户下单时支付的金额&#xff0c;这个最好理解 产品分成&#xff1a;也就是跟其他人合做以后我方能分到的金额&#xff0c;举个例子&#xff0c;比如用户订单金额是 100 块&#xff0c;我方的分成是 80%&#xff0c;那么也就是…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023