题目描述

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 

示例 2：

输入：height = [4,2,0,3,2,5]
输出：9

提示：

• n == height.length
• 1 <= n <= 2 * 10^4
• 0 <= height[i] <= 10^5

解题思路：

1.暴力解答：

每个位置处的积水取决于左右两边柱子的最低高度，分别从起始位置遍历到该位置得到左边的最高高度，然后从该位置遍历到末端，得到右边高度的最高值。因此计算每个位置处的积水量：等于该位置左右两边最高高度的最小值-该位置的高度。

代码：

class Solution {public static int trap(int[] height) {int sumVolume = 0;int i=0,len=height.length;for(;i<len;i++){int j=0,leftmax = i;while(j<i){if(height[j]>height[leftmax])leftmax = j;j++;}j=i+1;int rightmax = i;while(j<len){if(height[j]>height[rightmax])rightmax = j;j++;}sumVolume+=Math.min(height[leftmax],height[rightmax])-height[i];}return sumVolume;}
}

结果：

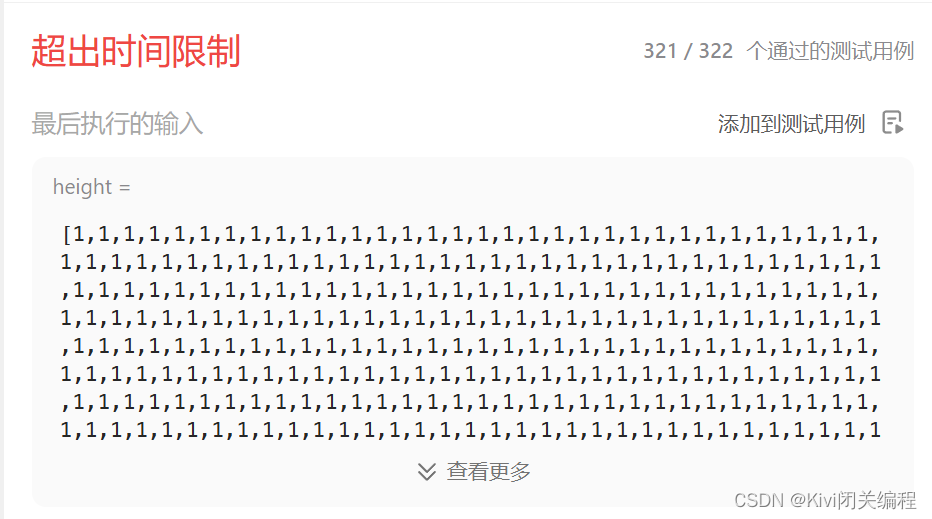
2.动态规划

上述暴力解法由于每次遍历i时都又遍历了一整遍数组，因此时间复杂度为O(n^2)，导致运行时间超时。因此采用动态规划的思想，提前遍历数组，确定好每个位置处的左边最高值和右边最高值。然后再按上述计算积水量方法计算总的积水量即可。
代码：

class Solution {public static int trap(int[] height) {int sumVolume = 0;int i=0,len=height.length;int curMaxHeight = 0;int[] leftMaxheigt = new int[len]; // 存储每个位置左边最高值int[] rightMaxheigt = new int[len]; // 存储每个位置右边最高值for(;i<len;i++){// 从前往后遍历height数组获取每个位置左边最高值if(height[i]>curMaxHeight){curMaxHeight = height[i];}leftMaxheigt[i] = curMaxHeight;}curMaxHeight=0;for(i=len-1;i>=0;i--){// 从后往前遍历height数组获取每个位置右边最高值if(height[i]>curMaxHeight){curMaxHeight = height[i];}rightMaxheigt[i] = curMaxHeight;}for(i=0;i<len;i++){sumVolume+=Math.min(leftMaxheigt[i],rightMaxheigt[i])-height[i];}return sumVolume;}
}

结果：

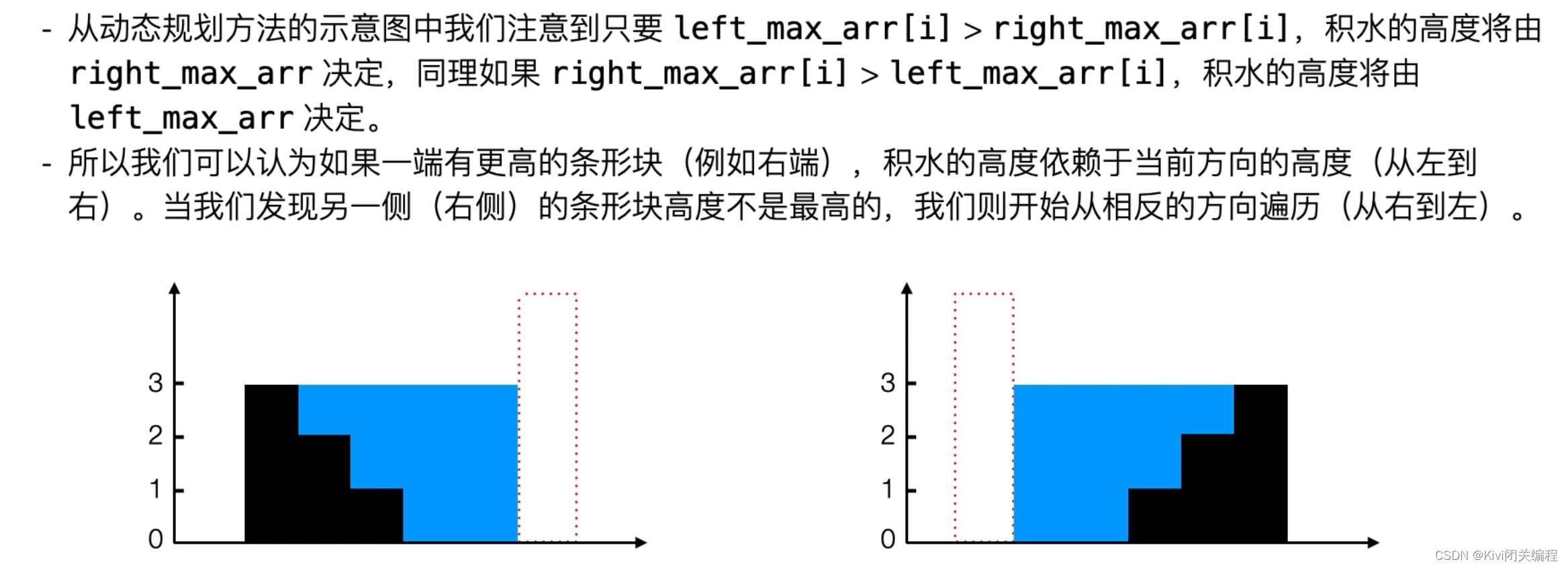
3.双指针

class Solution {public static int trap(int[] height) {int i=0,j=height.length-1;int leftMax=0,rightMax=0;int sumVolume=0;while(i<j){if(height[i]<height[j]){if(height[i]<leftMax){sumVolume += leftMax-height[i];}else{leftMax=height[i];}i++;}else{if(height[j]<rightMax){sumVolume += rightMax-height[j];}else{rightMax=height[j];}j--;}}return sumVolume;}
}

结果：