一方面,由于结构共振、测试噪声的干扰,为了确保分解精度,需要给定准确的参数初值(例如,瞬时频率)。研究人员通常认为零部件特征频率与通过传动比和驱动转速计算的理论值基本吻合,并基于理论值设置参数初值。事实上,由于传动误差、零部件惯性、频率分辨率、转速波动等因素的共同作用,传动系统的部分振动信号分量实测频率往往与理论频率存在偏差。为了对频率偏差现象进行说明,考虑某车辆传动装置台架的振动信号频谱,如下图所示。
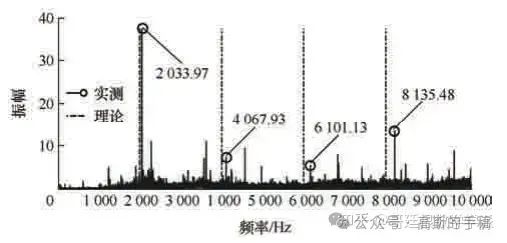
驱动端齿轮副啮合频率的实测基频与理论基频偏差为53.4Hz,实测四倍频与理论四倍频的偏差高达213.21Hz,这一偏差由大功率机械传动系统的传动误差、零部件惯性、频率分辨率、转速波动等多种因素共同导致,在分析此类信号时,若仍基于理论值设置参数初值,将导致分解结果中存在不可接受的误差。
另一方面,分量的存在性判定过程被忽略,导致无法确定分解结果的物理意义。工程测试的振动信号均为随机信号,任何频率对应的振幅均不为零,研究人员通常先验性地认为信号分量存在,并由此在未经验证的情况下判定分解分量的物理意义与假想保持一致。与军事通信、卫星导航、海洋声波等领域已经存在的基于振幅/能量的信号检测技术不同,传动系统的含偏差频率分量检测无法简单地借助于能量特征、信噪比等判据实现,这是由于传动系统的振动信号受结构共振和传递路径的影响,其频谱呈现出非线性包络特征,信号分量的存在与否与其振幅没有必然联系,也不依赖于其理论频率。
事实上,在传动系统信号分解中,信号分量检测问题尤其是含偏差频率分量检测问题没有受到足够的重视。上述两大挑战分别制约了信号分解的精度及物理可解释性,进而限制了其在传动系统信号特征提取中的有效应用。考虑旋转机械振动信号的基本特性,运动学同步能够协助正确识别并分析传动系统运行周期中的瞬态事件,仍以上图为例,尽管频率偏差现象难以避免,啮合频率基频及其高次谐波分量之间仍然近似满足谐波关系(6101.13/2033.97≈3,8135.48/2033.97≈4),从而启发学者借助同一谐波簇中含偏差频率分量间固有的谐波关系对其进行协同检测,以解决现有信号分解方法在精度与物理可解释性方面面临的问题。
工学博士,担任《Mechanical System and Signal Processing》《中国电机工程学报》《控制与决策》等期刊审稿专家,擅长领域:现代信号处理,机器学习,深度学习,数字孪生,时间序列分析,设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。




![[6] CUDA之线程同步](https://img-blog.csdnimg.cn/direct/bd6d3f1547714ea68616e881f66cb55c.png)