重点理解一下加减法的电路实现,先行进位的原理,以及时间延迟分析。挑重点记录一下我的理解。
定点加减法的运算
运算原理
在计算机内,定点数都是以补码的形式进行运算的。两个数 x , y x,y x,y 的加减法满足下面的规则:
{ [ x + y ] 补 = [ x ] 补 + [ y ] 补 [ x − y ] 补 = [ x ] 补 − [ y ] 补 = [ x ] 补 + [ − y ] 补 (1) \begin{cases}[x+y]_补=[x]_补+[y]_补\\ [x-y]_补=[x]_补-[y]_补=[x]_补+[-y]_补\end{cases}\tag 1 {[x+y]补=[x]补+[y]补[x−y]补=[x]补−[y]补=[x]补+[−y]补(1)
溢出检测
有符号数溢出的检测有 3 3 3 种方法。最简单的就是看加数 x , y x,y x,y 和和数 s s s 的符号位,当 x , y x,y x,y 同号且与 s s s 异号就说明溢出了,简单来说就是负负得正、正正得负算溢出。

图1 方法一:符号位溢出检测
另外还有 2 2 2 种方法。
方法二:比较符号位进位与最高位进位
用 C f C_f Cf 表示符号位进位, C n C_n Cn 表示最高位进位,则溢出标志:
O F = C f ⊕ C n (2) OF=C_f\oplus C_n\tag 2 OF=Cf⊕Cn(2)
见下面的例子:

图2 方法二示意图
下面说明一下这个式 ( 2 ) (2) (2) 的正确性:
☞ 当两个数都是正数的时候,符号位的进位肯定是 C f = 0 C_f=0 Cf=0。此时当且仅当最高位不产生进位,即 C n = 0 C_n=0 Cn=0,和数的符号位为 0 0 0,相加的结果是一个正数,即不会溢出。此时不溢出当且仅当 C f = C n = 0 C_f=C_n=0 Cf=Cn=0。
☞ 当两个数都是负数的时候,符号位的进位肯定是 C f = 1 C_f=1 Cf=1。此时当且仅当最高位产生进位,即 C n = 1 C_n=1 Cn=1,和数的符号位为 1 1 1,相加的结果是一个负数,即不会溢出。此时不溢出当且仅当 C f = C n = 1 C_f=C_n=1 Cf=Cn=1。
☞ 两个数一正一负,这种情况肯定是不会溢出的。一正一负说明符号位相加刚好是 1 1 1,这个时候看最高位:如果最高位有进位 C n = 1 C_n=1 Cn=1,那么符号位的部分和 1 1 1 加上最高位进位来的 1 1 1,导致符号位也产生进位 C f = 1 C_f=1 Cf=1;如果最高位没有进位 C n = 0 C_n=0 Cn=0,那么符号位就确定是 1 1 1 且没有进位 C f = 0 C_f=0 Cf=0。此时 C f ⊕ C n C_f\oplus C_n Cf⊕Cn 恒为 0 0 0。
方法三:使用双符号位
在原本的符号位左边再增加一个新的符号位,构成双符号位。这种方法只适用于手动运算;计算机比人抽象、聪明,所以不需要这种东西。
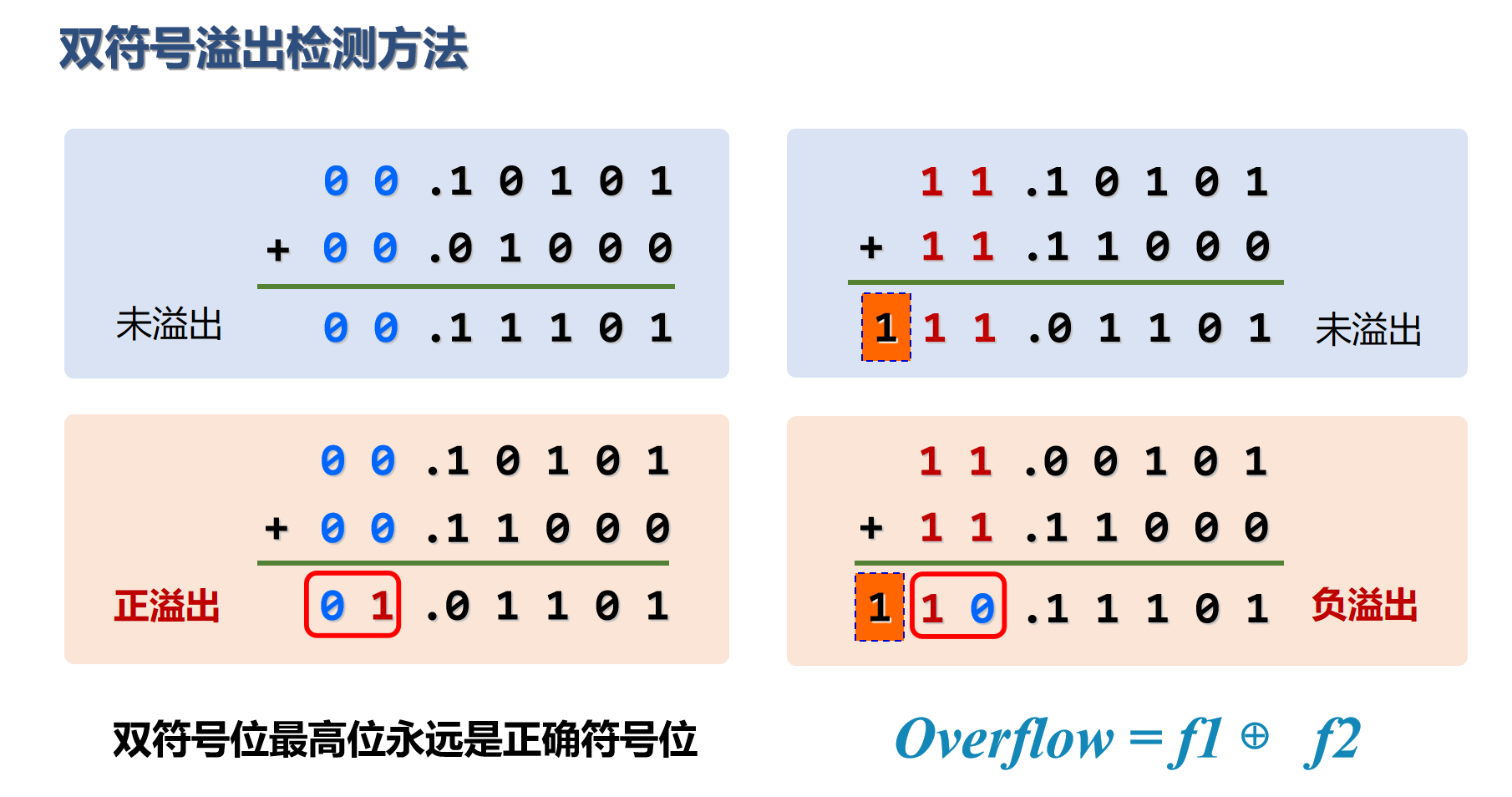
图3 方法三示意图
这种方法其实和方法二是一样的,正确性的说明也可以分都是正数、都是负数、一正一负三种情况来讨论。
电路实现
一位全加器
计算机内的加法,靠的是一位全加器这个基本单元。
一位全加器输入两个加数 X i , Y i X_i,Y_i Xi,Yi,来自低位的进位 C i C_i Ci,输出进位 C i + 1 C_{i+1} Ci+1 与和数 S i S_i Si。这些都是 1 bit 的。其中 S i S_i Si:
S i = X i ⊕ Y i ⊕ C i (3) S_i=X_i\oplus Y_i\oplus C_i\tag 3 Si=Xi⊕Yi⊕Ci(3)
C i + 1 C_{i+1} Ci+1 可以由下面两种方式得到:
C i + 1 = X i Y i + ( X i ⊕ Y i ) C i (4) C_{i+1}=X_iY_i+(X_i\oplus Y_i)C_i\tag 4 Ci+1=XiYi+(Xi⊕Yi)Ci(4) C i + 1 = X i Y i + ( X i + Y i ) C i (5) C_{i+1}=X_iY_i+(X_i+Y_i)C_i\tag 5 Ci+1=XiYi+(Xi+Yi)Ci(5)
可以看到 ( 4 ) (4) (4) 复用了 ( 3 ) (3) (3) 中 X i ⊕ Y i X_i\oplus Y_i Xi⊕Yi 的结果,所以实际实现中 ( 4 ) (4) (4) 比 ( 5 ) (5) (5) 需要的门电路更少,这意味着它的硬件开销更小,故而采用 ( 4 ) (4) (4) 去电路中实现 C i + 1 C_{i+1} Ci+1 的计算。


图4 一位全加器示意图及内部门电路延迟图
串行加法器
串行加法器原理与溢出分析
将 n n n 个一位加法器串联,可以生成 n n n 位串行加法器。下面的图中, S u b = 1 \mathit{Sub}=1 Sub=1 代表进行减法 S = X − Y S=X-Y S=X−Y, S u b = 0 \mathit{Sub}=0 Sub=0 代表进行加法 S = X + Y S=X+Y S=X+Y。
需要注意的是,加法器不区分有符号数和无符号数。根据输入进来的数据,加法器按照有符号数、无符号数的解释分别设立溢出标志(有符号溢出、无符号溢出),由程序的编写者根据实际情况选择使用哪个标志。

图5 串行加法器电路图
图中的 o v e r f l o w \mathit{overflow} overflow 是有符号溢出标志,该电路的实现用到了前文溢出检测方法二。该加法电路还需要设置一个无符号溢出标志,这个溢出标志是 S u b ⊕ C n \mathit{Sub}\oplus C_n Sub⊕Cn。下面分加法、减法两种情况说明这个溢出标志的正确性。
对于加法的情况, S u b = 0 \mathit{Sub}=0 Sub=0。有符号加法溢出,那就是符号位产生了进位 C n = 1 C_n=1 Cn=1,所以加法时的溢出标志是 C n C_n Cn。
对于减法的情况,稍微麻烦一些。此时 S u b = 1 \mathit{Sub}=1 Sub=1,执行的计算是 S = X − Y S=X-Y S=X−Y,送入加法器的是 X X X 和 Y ′ Y' Y′( Y ′ = [ − Y ] 补 Y'=[-Y]_补 Y′=[−Y]补)。无符号减法溢出,就是被减数小于减数,得到的差是个负数,不能用无符号数表示,自然就溢出了。也就是说溢出的条件是 X < Y X<Y X<Y。显然对于 n n n 位加法器来说,有 Y ′ + Y = 2 n Y'+Y=2^n Y′+Y=2n,因此溢出条件也可以写作 X < 2 n − Y ′ X<2^n-Y' X<2n−Y′,也即 X + Y ′ < 2 n X+Y'<2^n X+Y′<2n。这时只有加法器的符号位不产生进位,才能说减法操作没有溢出。所以减法时的溢出标志是 C n ‾ \overline {C_n} Cn。
串行加法器延迟分析
任何一个门电路都有时间延迟。在后文的讨论中,认为与门、或门、非门的延迟均为 T T T,异或门的延迟为 3 T 3T 3T。因为异或门可以看作是两个非门、两个与门、两个或门串接形成的。

图6 串行加法器延迟分析
上图中,所有的 X , Y X,Y X,Y 信号以及 C 0 C_0 C0 信号都是在 0 0 0 时刻输入的,数据线上的时间代表其中数据达到稳定状态的最短时间。 F A 0 \mathit{FA}_0 FA0 的时间延迟是很好分析的,通过图 4(右)就能很好地理解。关键是后面的全加器,在进位信号 C i C_i Ci 进来后,只需要 2 T 2T 2T 时间(而不是 5 T 5T 5T)就可以形成 C i + 1 C_{i+1} Ci+1,只需要 3 T 3T 3T 时间(而不是 6 T 6T 6T)就可以形成 S i S_i Si。
原因是,对于 F A 0 \mathit{FA}_0 FA0 之后的全加器,它们的 C i C_{i} Ci 信号到来时, X i ⊕ Y i X_i\oplus Y_i Xi⊕Yi 和 X i Y i X_iY_i XiYi 信号都已经生成好了。这一点是 F A 0 \mathit{FA}_0 FA0 所不具备的,当 C 0 C_0 C0 信号到来的时候, X 0 ⊕ Y 0 X_0\oplus Y_0 X0⊕Y0 和 X 0 Y 0 X_0Y_0 X0Y0 都还在形成的过程中。

图7 后续全加器延迟分析
图 6 是对 F A 0 \mathit{FA}_0 FA0 之后的加法器的延时分析。蓝色信号早在 t t t 时刻之前就已经准备就绪,在 t t t 时刻 C i C_{i} Ci 信号进入,红色信号标明了各数据线上最终形成稳定数据的时间。
并行加法器
串行加法器太慢了。当位数 n n n 多起来的时候,时间开销会以 O ( n ) O(n) O(n) 的速度增长。分析一下上面的电路,主要是因为后一个加法器依赖于前一个加法器的进位输出,那我们只要提前把这些进位都算出来就好了。
回顾式 ( 3 ) ( 4 ) (3)(4) (3)(4),我们令进位生成函数 G i = X i Y i G_i=X_iY_i Gi=XiYi,进位传递函数 P i = X i ⊕ Y i P_i=X_i\oplus Y_i Pi=Xi⊕Yi。那么式 ( 3 ) ( 4 ) (3)(4) (3)(4) 可分别写为:
S i = P i ⊕ C i (6) S_i=P_i\oplus C_i\tag 6 Si=Pi⊕Ci(6) C i + 1 = G i + P i C i (7) C_{i+1}=G_i+P_iC_i\tag7 Ci+1=Gi+PiCi(7)
利用式 ( 7 ) (7) (7) 进行迭代,就可以用各个 G , P G,P G,P 和 C 0 C_0 C0 来表示 C i ( i > 0 ) C_i(i>0) Ci(i>0):
C n = G n − 1 + P n − 1 G n − 2 + P n − 1 P n − 2 G n − 3 + ⋯ + P n − 1 P n − 2 ⋯ P 1 P 0 C 0 (8) C_n = G_{n-1}+P_{n-1}G_{n-2}+P_{n-1}P_{n-2}G_{n-3}+ \cdots+P_{n-1}P_{n-2}\cdots P_1P_0C_0 \tag8 Cn=Gn−1+Pn−1Gn−2+Pn−1Pn−2Gn−3+⋯+Pn−1Pn−2⋯P1P0C0(8)
下面用一张图来形象的描述进位生成函数和传递函数, C 1 = G 0 + P 0 C 0 C_1=G_0+P_0C_0 C1=G0+P0C0, 只有 P 0 P_0 P0 阀门打开时, C 0 C_0 C0 装的水才可能流出到 C 1 C_1 C1, 所以 P 0 P_0 P0 称为传递函数;而 G 0 G_0 G0 阀门一打开,水就流出到 C 1 C_1 C1,所以 G 0 G_0 G0 称为生成函数。
将多个阀门串接在一起可以得到 C 2 C_2 C2, C 4 C_4 C4 的逻辑,以 C 4 C_4 C4 为例, C 0 C_0 C0 的水要流到 C 4 C_4 C4,必须同时打开所有 P P P,也就是这里的 P 3 , P 2 , P 1 , P 0 , C 0 P_3,P_2,P_1,P_0,C_0 P3,P2,P1,P0,C0。
以 4 4 4 位先行进位加法器为例,构建并行加法器主要有三大部件。
生成传递函数电路:与门、异或门阵列
按照我们对 G G G 和 P P P 的定义,可以构造下面的电路。这个电路的时间延迟是 3 T 3T 3T。

图8 与门、异或门阵列
先行进位电路
我们已经得到了所有的 G , P G,P G,P。根据式 ( 8 ) (8) (8) 可以构建下面的电路。 这个电路有 2 T 2T 2T 的时间延迟。
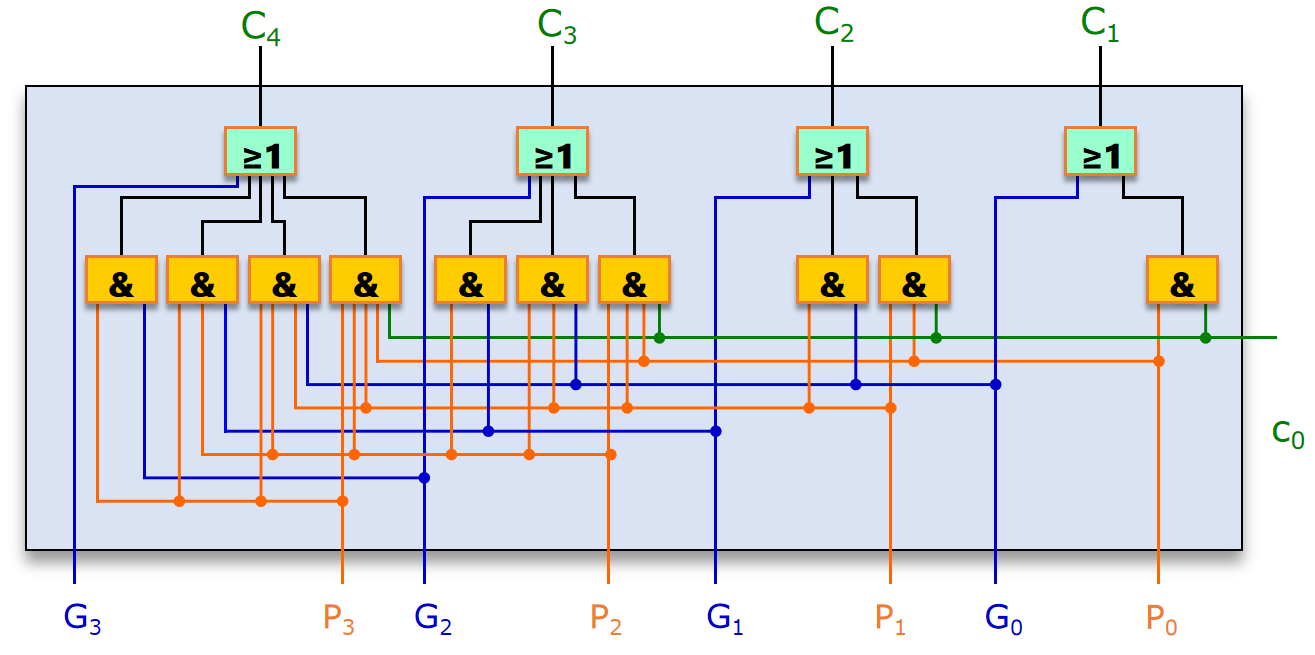
图9 先行进位电路
求和电路
我们已经得到了所有的 P P P 和 C C C。根据式 ( 6 ) (6) (6),可以之间使用 4 4 4 个异或门获取 S 0 S_0 S0~ S 4 S_4 S4。由于异或门的时间延迟是 3 T 3T 3T,这一部件的时间延迟也就是 3 T 3T 3T。
所以,总的电路图如下所示。生成最终进位信号 C 4 C_4 C4 的时间是 5 T 5T 5T,而生成最终和数 S S S 的时间是 8 T 8T 8T。
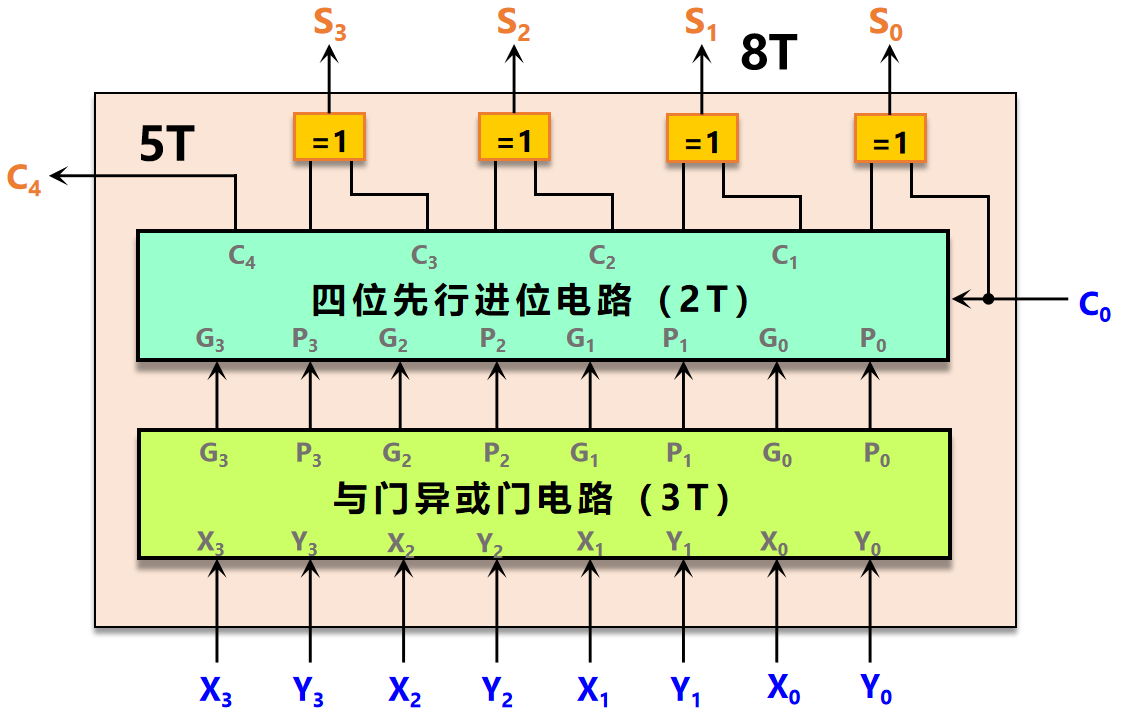
图10 4 位先行进位快速加法器
16 位加法器
串行构建
前面已经得到了 4 4 4 位并行加法器。可以将这样的加法器进行 4 4 4 个的串联,从而得到 16 16 16 位加法器。

图10 4 位先行进位快速加法器
从图 10 你能看到,这个加法器无非就是 4 4 4 位一组、组间串行。而 4 4 4 位串行加法器也可以看成是 1 1 1 位一组、组间串行。因此它的延迟分析和 4 4 4 位串行加法器差不多——当 C 4 C_4 C4 产生的时候, C 8 C_8 C8 会在 2 T 2T 2T(而不是 5 T 5T 5T)后产生, S 4 S_4 S4~ S 7 S_7 S7 会在 5 T 5T 5T (而不是 8 T 8T 8T) 后产生。
并行构建
图 10 中的加法器, C 4 i + 4 C_{4i+4} C4i+4 的生成依赖 C 4 i C_{4i} C4i。仿照 4 4 4 位并行加法器的构建思路,图 10 中的 4 4 4 个快速加法器也可以采取组间并行的方式。也就是通过 C 0 C_0 C0 直接得到 C 4 , C 8 , C 12 , C 16 C_4,C_8,C_{12},C_{16} C4,C8,C12,C16。
由 ( 7 ) (7) (7) 我们知道 C 1 = G 0 + P 0 C 0 C_1=G_0+P_0C_0 C1=G0+P0C0。我们是不是也能弄出一个 C 4 = G ∗ + P ∗ C 0 C_4=G^*+P^*C_0 C4=G∗+P∗C0?

图11 成组进位函数
当然可以,如图 11 所示。此时先行进位电路需要生成两个新的信号 G ∗ , P ∗ G^*,P^* G∗,P∗,电路由图 9 改成图 12。
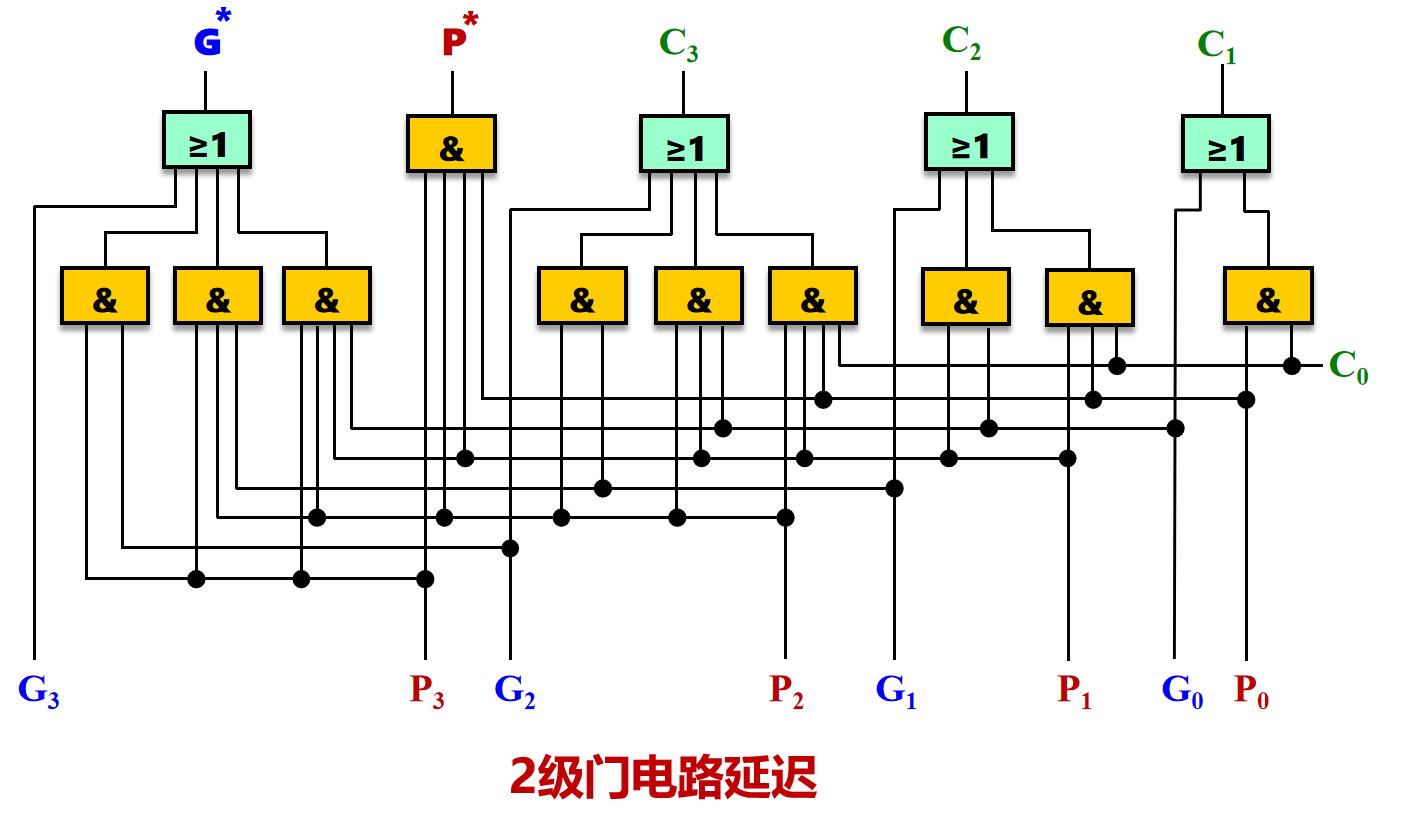
图11 成组进位函数
此时的电路图及延时分析如下图所示。
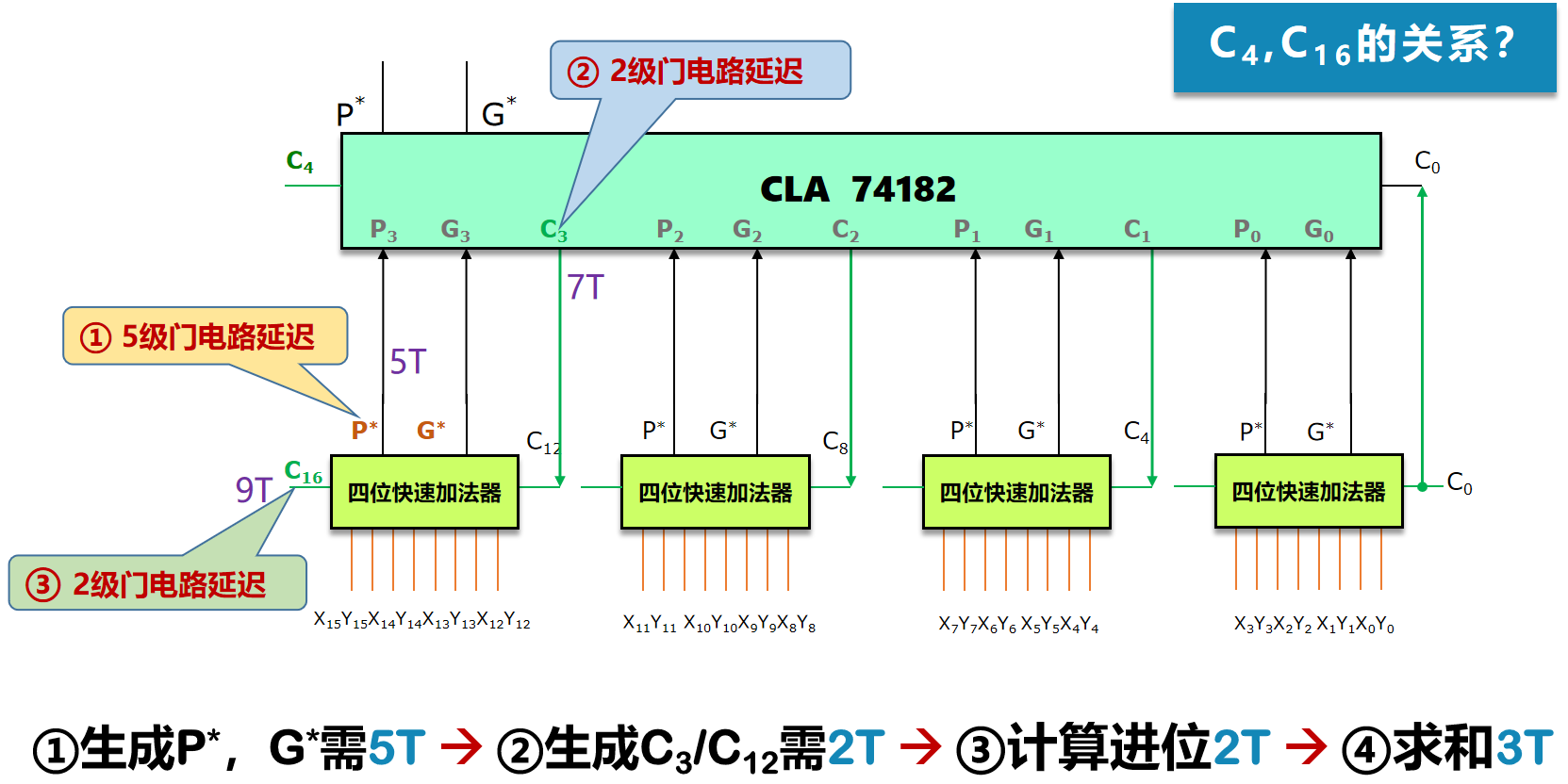
图12 16 位先行进位电路图及延时分析
64 位加法器
在 16 位的基础上,还可以组间并行,有点套娃的意思了。电路图如下所示:
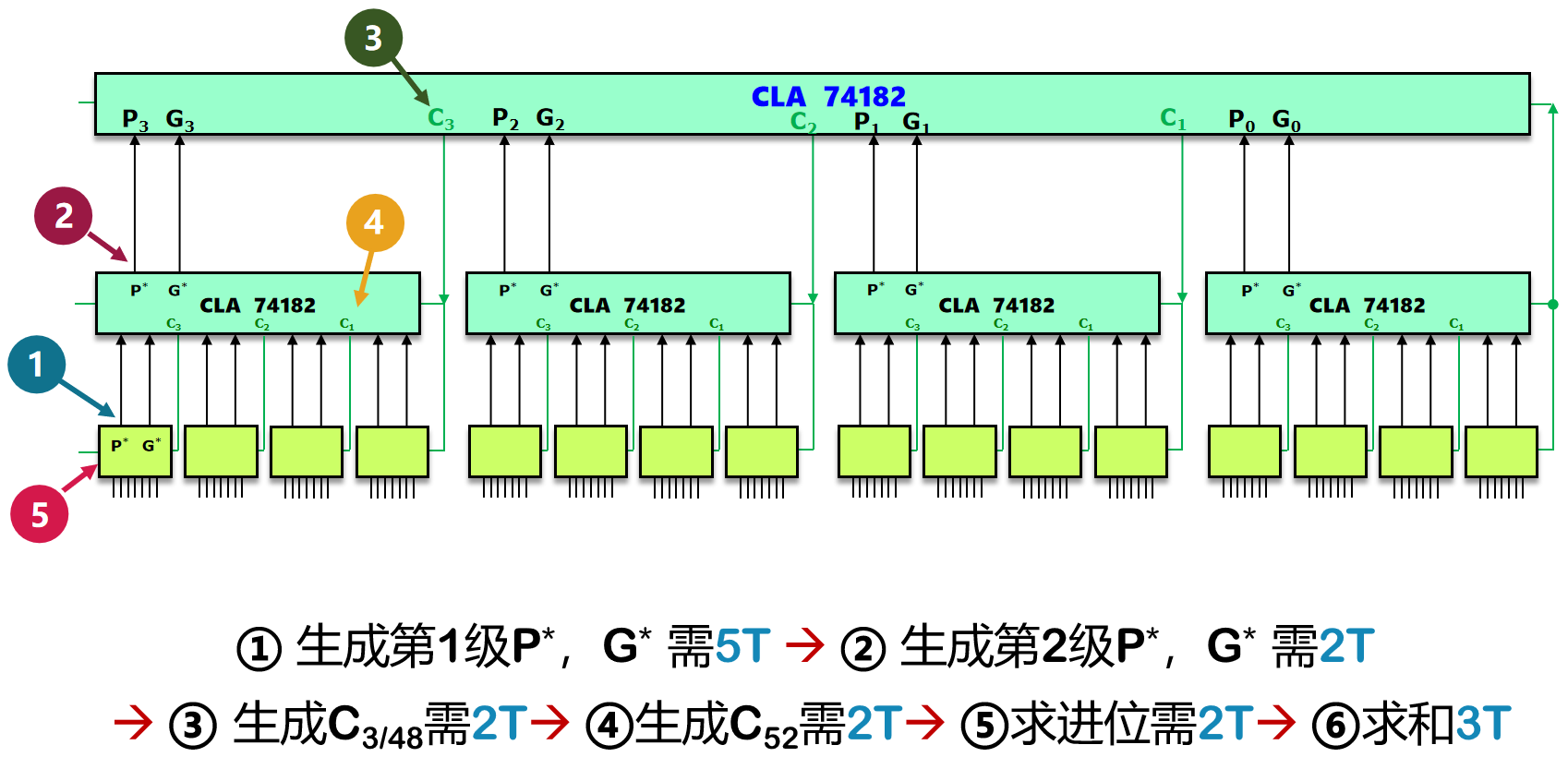
图13 64 位先行进位电路图及延时分析
比对一下图 13 和图 11,可以发现它只多了向二级先行进位电路(图中蓝色的 CLA 74182),多出了 4 T 4T 4T 的时间。也就是说,位数 n n n 每扩大 4 4 4 倍,时间延迟增加 4 T 4T 4T。对于 n n n 位加法器而言,串行加法器的时间开销是 O ( n ) O(n) O(n),并行加法器的时间开销只需要 O ( log n ) O(\log n) O(logn)。




![[数据集][目标检测]红外车辆检测数据集VOC+YOLO格式13979张类别](https://img-blog.csdnimg.cn/direct/17457a91173845208f30064ac8d094c2.png)