动规算法-地下城游戏

在这里插入图片描述

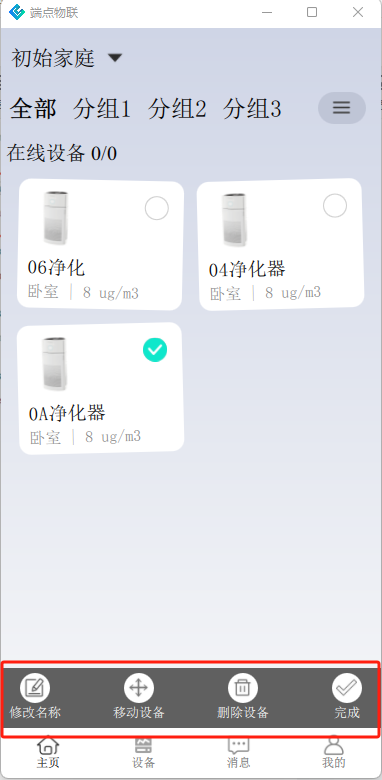
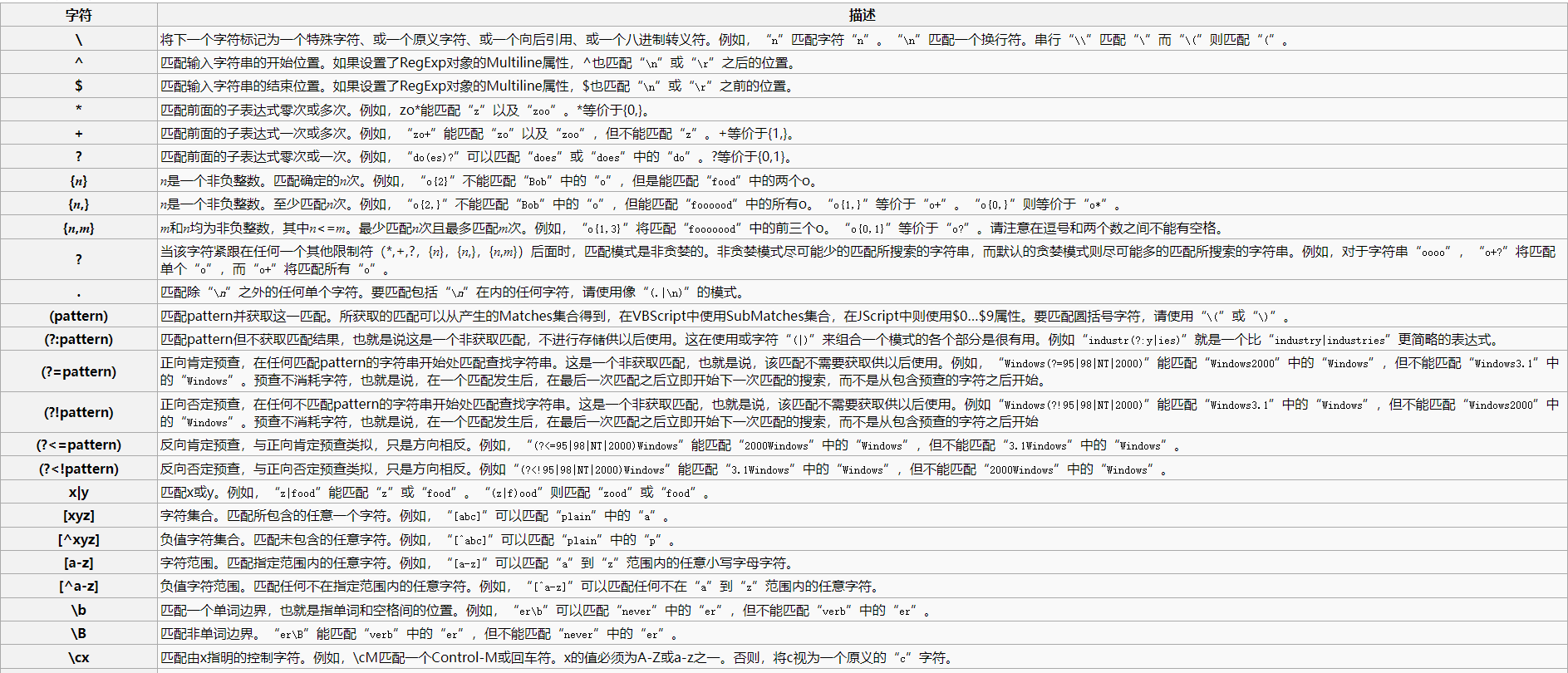
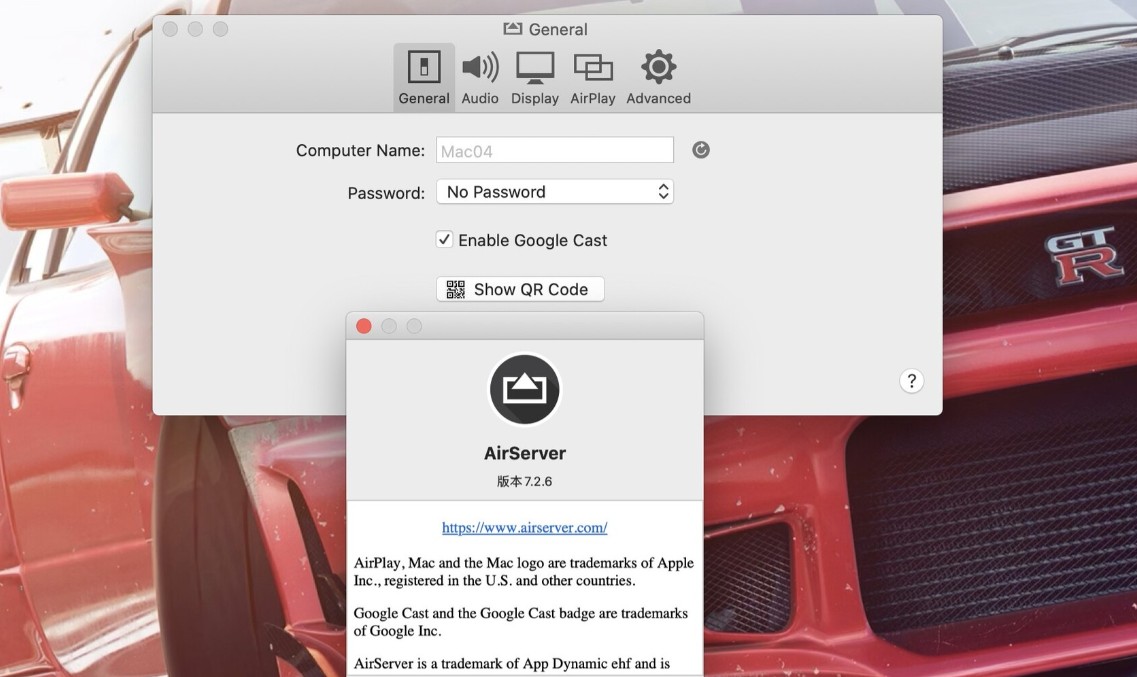
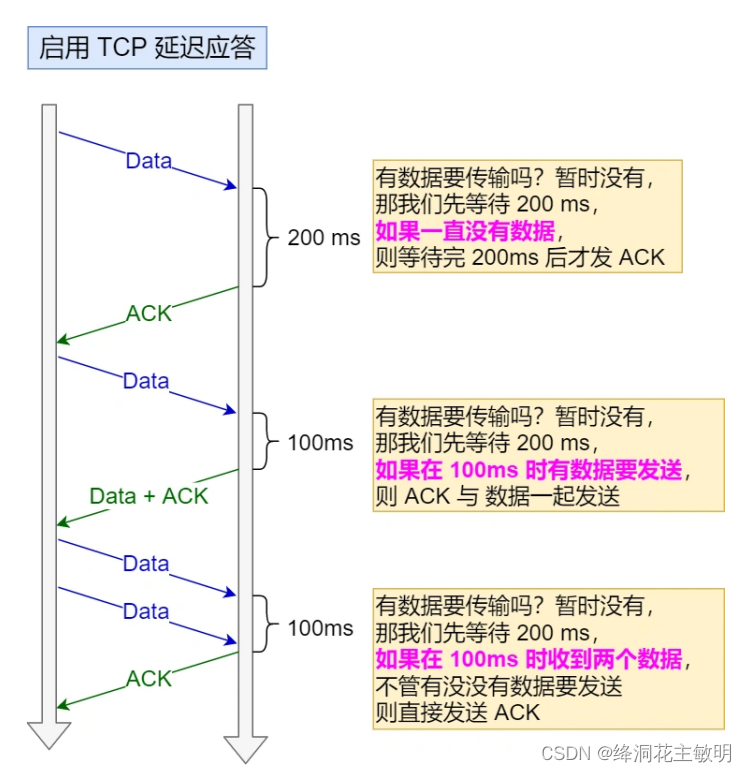
在刷题练习专栏中，已经写了两篇文章实现对动态规划入门题目的讲解了，动态规划这类题目很难很好的掌握，今天给大家带来稍微深入的题目，帮助大家更好的理解动态规划的算法思想，加深对该算法的理解，建议看每道题之前可以自己尝试做一做，然后再看一看我的思路，做题步骤会延续之前的方法。
第一题
地下城游戏
在这里插入图片描述
这道题一定要读懂题意，遇到像这样的题目，一定要注意细节，防止看错后边很难修改。
这道题下边的注意也要读懂，意思是，救到公主后我们的血量至少为1。
这道题乍一看是一道普通的路径选择问题，但是因为一个限制条件，让这道题在leetcode中标记为困难，首先来看示例，明白题目和分析状态表示。
在这里插入图片描述
在前边的题目中，我们有过两种分析思路，分别是以某位置为开始和以某位置为结尾两种分析方式，在前边的题目中这两种方式都是可以解决问题的，但是在这道题目中，有一种方式是不可以的，就是因为前边的限制条件。
为了更好讲解这道题目，可以先来看一看这道题
最小路径和
这道题虽然简单，但是对我们理解这道题目很有帮助。
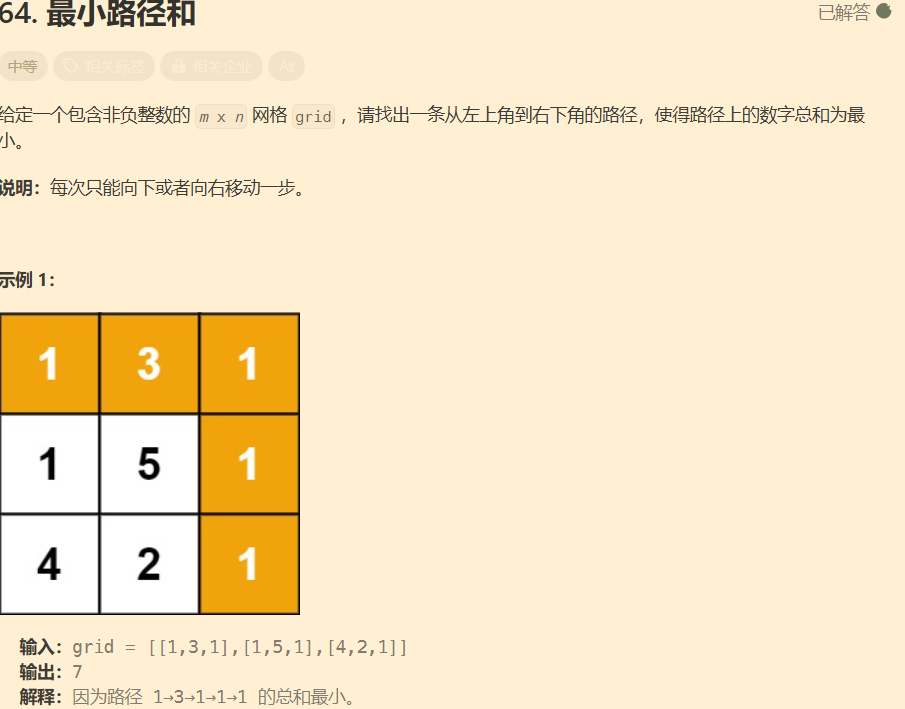
在这里插入图片描述
用这道题作为例子深刻理解以某位置为开始和以某位置为结尾两种思路来做这道题。
第一种思路，先来一个容易理解一点的，那就是以某位置为开始。
对于这道题，状态表示为，从左上角开始，到达i,j位置产生的最小路径和。如果你对动态规划有了了解，相信你能很快解决这道问题。
代码如下（有详细注释）

int minPathSum(vector<vector<int>>& grid) {int m=grid.size(),n=grid[0].size();vector<vector<int>> dp(m+1,vector<int> (n+1,INT_MAX));//创建dp表dp[0][1]=dp[1][0]=0;//为了不影响后边的数据.for(int i=1;i<=m;i++)for(int j=1;j<=n;j++)dp[i][j]=min(dp[i-1][j],dp[i][j-1])+grid[i-1][j-1];//这里与原数组的对应关系一定要控制好return dp[m][n];}

画图表示该过程的话就是下图。
在这里插入图片描述
接下来是第二种思路，那就是以某个位置为起点。
在这道题目中，状态表示即为从i,j位置开始，到达右下角位置的最小路径和。

//以某位置为起点int minPathSum(vector<vector<int>>& grid) {int m=grid.size(),n=grid[0].size();vector<vector<int>> dp(m+1,vector<int> (n+1,INT_MAX));dp[m-1][n]=0,dp[m][n-1]=0;for(int i=m-1;i>=0;i--){for(int j=n-1;j>=0;j--){dp[i][j]=min(dp[i+1][j],dp[i][j+1])+grid[i][j];}}       return dp[0][0];}

如下图
在这里插入图片描述
这道题一定要好好思考思考，要注意因为他们的状态表示不同，所以返回值也不同。

看完上面所述题目后，正式开始分析这道题。
实例1如下：
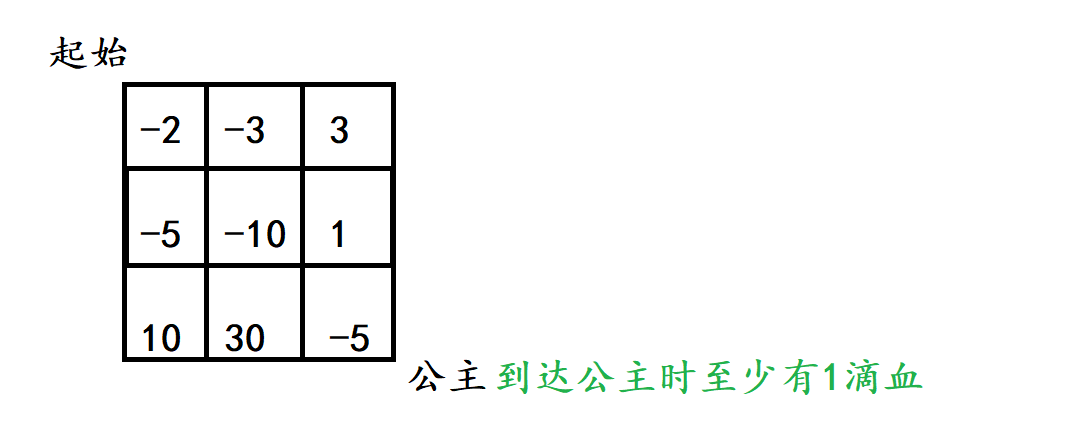
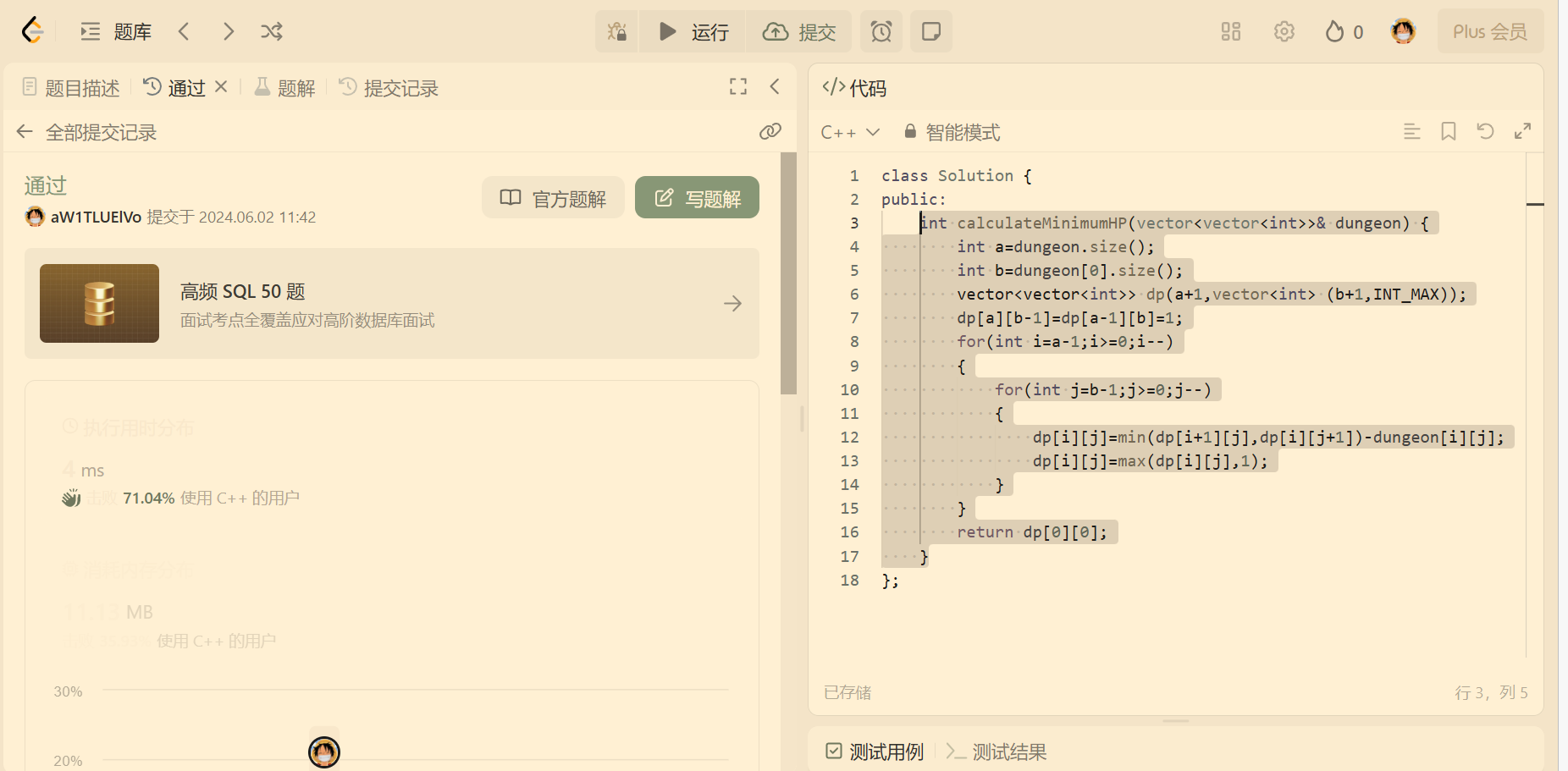
在这里插入图片描述
第一种分析思路，就是以某位置为结尾这种思路，状态表示dp[i][j]表示从起点出发，到达（i,j）位置所需最小初始健康量。有了上边拿到题目的铺垫。以这道题为例子，就是左下角向右上角填。

按上边的状态表示来做的话，状态表示为从初始位置出发，到达i,j位置时所需要的最小血量。如果我们想要从第一个位置杀出去，我们至少需要3滴血，但是我们怎么能保证我们判断的3是正确的呢？怎么保证我们找出的数正好是解救公主最少的血量呢？我们不能保证。因为用这种思路在判断某个位置的结果时，不仅会受到前边的状态的影响，还会受到后边表格中的值的影响。通过前边的表格中的值，只能找到能够到达下一位置需要的健康值，而是否能够解救公主，还需要通过后边路径中的值来判断的，所以我们填出的值不符合无后效性。

无后效性是指一个问题可以用动态规划求解的标志之一。具体地说，如果一个问题被划分各个阶段之后，阶段I中的状态只能由阶段I+1中的状态通过状态转移方程得来，与其它状态没有关系，特别是与未发生的状态没有关系。

所以这道题目只能用第二种思路，那就是以某位置为结尾这种思路来完成。

状态表示
从i,j位置出发，到达右下角位置所需要的最低生命值。这种分析思路是可行的。可以从后往前递推出最终结果。
状态转移方程
分析状态方程要注意题意，我们从最后一个位置出去才能成功救助公主，所以要想从该位置出去并且能成功到达下一位置，状态表示为dp[i][j]=min(dp[i+1][j],dp[i][j+1])-dungeon[i][j];
画图演示一下

还需要有一个注意的是，就像图中30的位置，因为该血包很大，所以得出dp值可能会变成负数，但是我们已经在到达dp[i][j]位置挂了，又怎么能吃到血包呢？所以得出的该位置的dp值要和1做一次max。
初始化
老套路，需要填表时不能影响最终结果，左下角位置特殊一点。画图
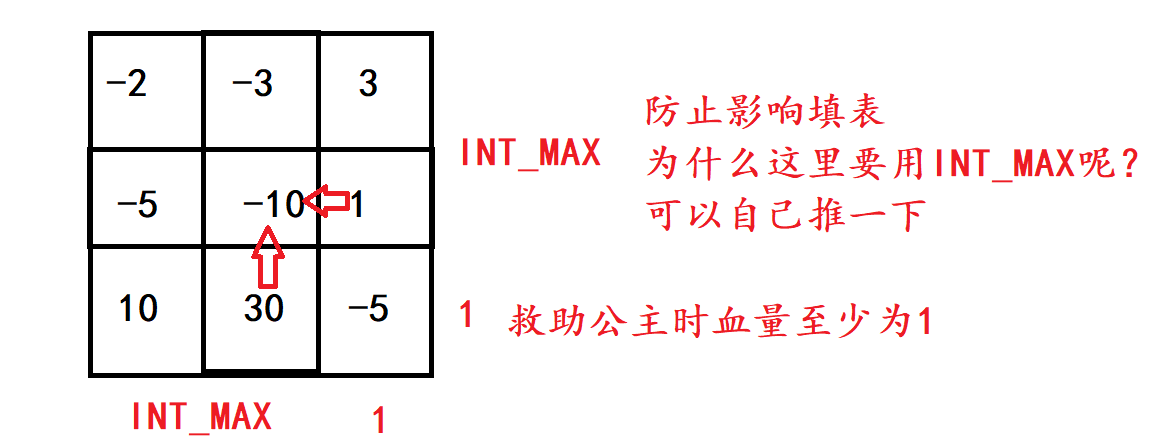
填表顺序
有了那一道题，我想这里很容易得出是从右下角往左上角填
返回值
根据状态表示可以知道，返回的是dp[0][0]位置的值。

最终代码

int calculateMinimumHP(vector<vector<int>>& dungeon) {int a=dungeon.size();int b=dungeon[0].size();vector<vector<int>> dp(a+1,vector<int> (b+1,INT_MAX));dp[a][b-1]=dp[a-1][b]=1;for(int i=a-1;i>=0;i--){for(int j=b-1;j>=0;j--){dp[i][j]=min(dp[i+1][j],dp[i][j+1])-dungeon[i][j];dp[i][j]=max(dp[i][j],1);}}return dp[0][0];}