目录

一、题目描述

二、初次解答

三、官方解法

四、总结

---

一、题目描述

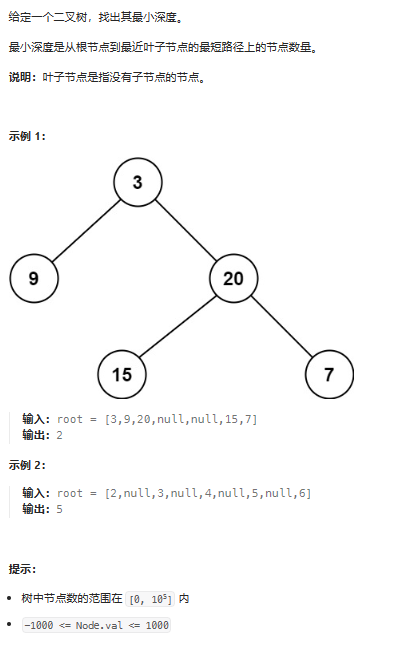
二、初次解答

1. 思路：二叉树的先序遍历。求出左子树的最小高度，求出右子树的最小高度，最终返回左子树和右子树的最小高度+1。关键：若左子树的高度为0，则返回右子树的最小高度+1；若右子树的高度为0，则返回左子树的最小高度+1；若左右子树都不为空，则返回左子树与右子树的最小高度。

2. 代码：

int minDepth(struct TreeNode* root) {//根节点为空if(!root)return 0;//叶子节点if(!(root->left) && !(root->right))return 1;int minLeft=minDepth(root->left);   //递归左子树int minRight=minDepth(root->right); //递归右子树if(minLeft==0) return minRight+1;   //左子树无节点if(minRight==0) return minLeft+1;   //右子树无节点return minLeft>minRight?minRight+1:minLeft+1;   //左右子树的最小高度
}

3. 优点：仅遍历一遍二叉树，时间复杂度为O(n)。

4. 缺点：采用了递归，空间复杂度为O(H)，H为树的高度。

三、官方解法

官方解法一的深度优先遍历与上述解法类似。解法二的广度优先遍历需要手动维护队列且空间复杂度不如解法一，因此不展开说明。

四、总结

求二叉树的最小深度：使用二叉树的先序遍历，递归求出左子树和右子树的最小深度，并考虑到左子树和右子树为空的情况。