基础
空间域与变换域
空间域:认为是图像本身,对于空间域的操作就是对图像中的像素直接进行修改
变换域:变换系数处理,不直接对于图像的像素进行处理
邻域
图像中某点的邻域被认为是包含该点的小区域,也被称为窗口
空间滤波
邻域选择空间域中的一小块区域,对于邻域中的像素运用算子T,并在该位置产生一个输出;随后将邻域的原点移动到下一个位置,并且重复前面的过程,生成下一个位置的值,当邻域的大小为1*1的时候,输出像素只取决于输入像素,而与周边像素无关
灰度变换函数
(1)反转变换:s = (L-1) - r
r为输入图像像素,s为输出图像像素,[0,L-1]为图像的灰度集
作用:使黑白反转
(2)对数变换: s = c log ( 1 + r ) s= c\log(1+r) s=clog(1+r)
c为常数,r>=0,使用对数变换可以让原图的灰度进行压缩,避免超出设备的限制,如图所示,将较低的灰度提高到了中间,同理还有其他变换函数也能起到相同或者相反的作用
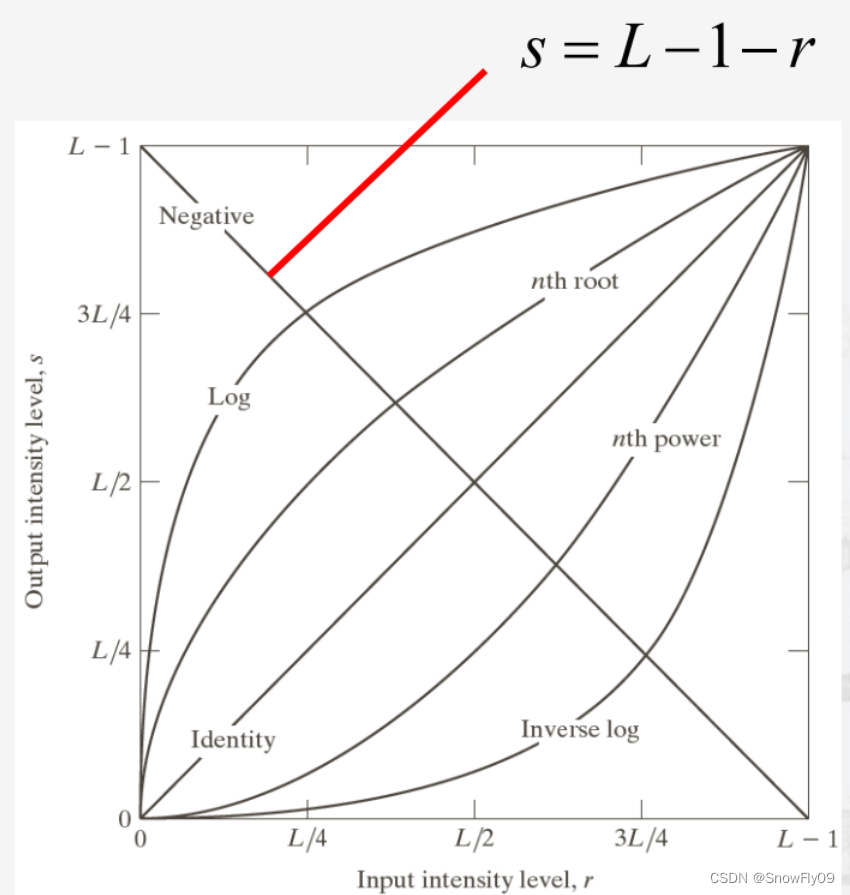
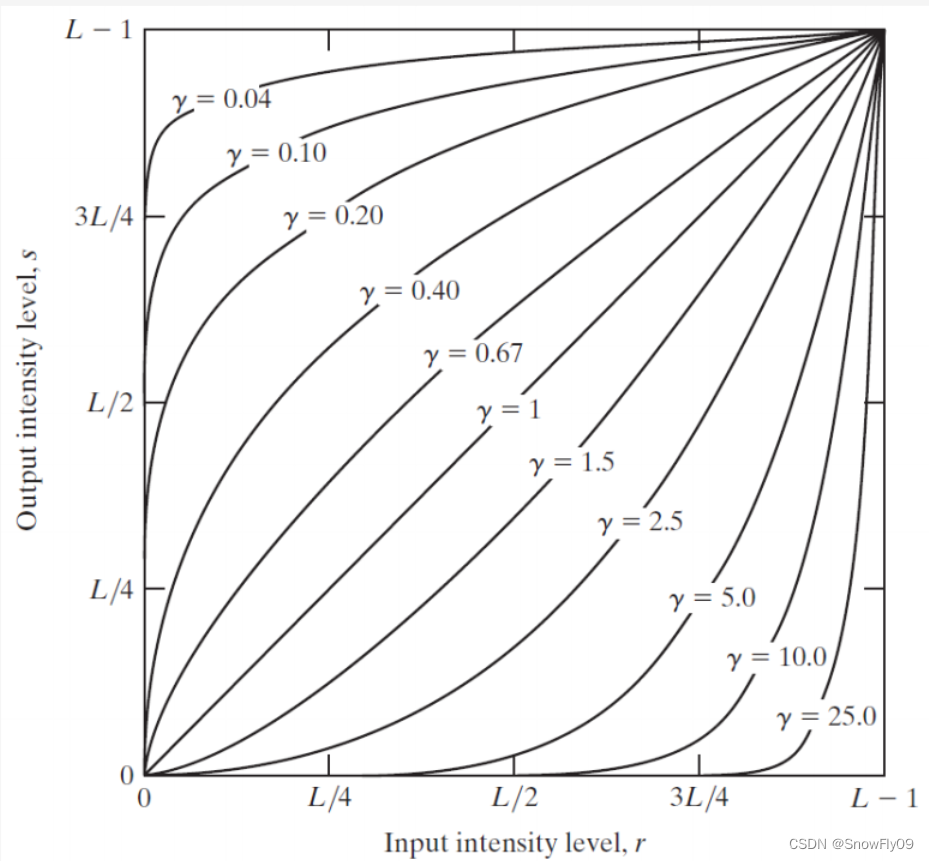
(3)幂变换: s = c ⋅ r γ s=c\cdot r^\gamma s=c⋅rγ
gamma小于1的时候,提高了灰度级,gamma大于1时,降低了灰度级
(记住图片就好)
直方图处理(重要)
对于一个灰度级范围为[0,L-1]的数字图像,其直方图表示为 h ( r k ) = n k h(r_k) = n_k h(rk)=nk,其中rk代表着第k级灰度,nk是图像中处在该灰度级的像素个数
归一化: p ( r k ) = h ( r k ) / M N p(r_k)=h(r_k)/MN p(rk)=h(rk)/MN
p是灰度级在图像中出现的概率估计,所有分量加起来之和为1
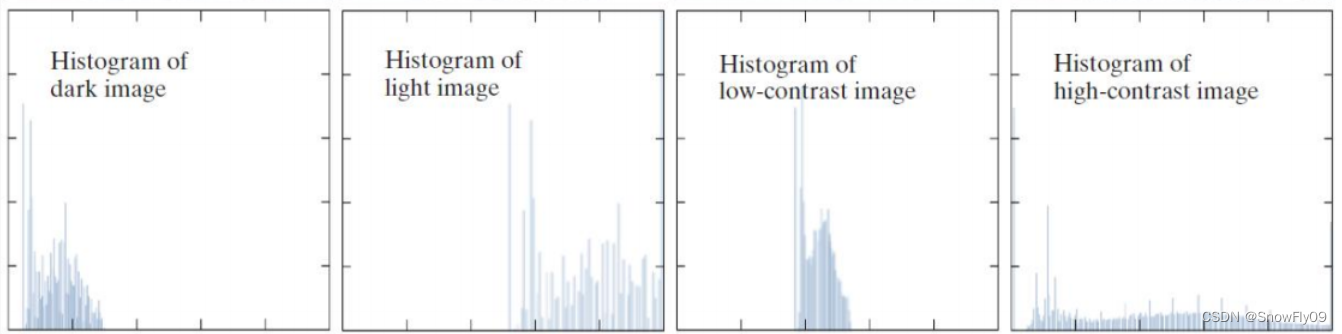
从左至右分别为暗图片,两图片,低对比度图片,高对比度图片
直方图均衡
目的就是将聚集在一起的灰度值变得“平坦”得分布在所有灰度级上,从最终结果上来说可以认为增加了对比度,同时将过亮或者过暗的图片调整正常。
这里我们不对于直方图均衡的具体原理进行细究,如想了解清楚请查看此处:直方图均衡化原理
理想情况下,均衡后的连续函数会使所有灰度级的概率密度全部相等
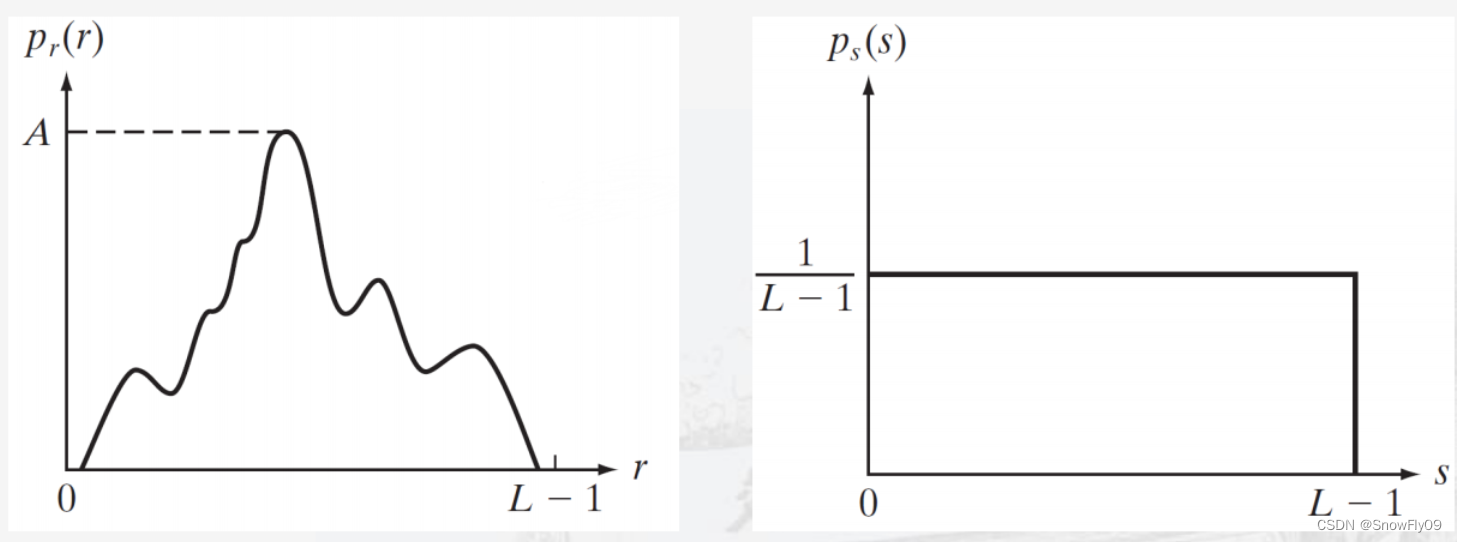
以下为实际遇到时的处理:
(这里也可以跳转我之前做过的直方图均衡/匹配实验,内含matlab代码:https://blog.csdn.net/weixin_46876169/article/details/137008120?spm=1001.2014.3001.5501)
e.g.一幅图大小为64*64,其灰度级范围为[0,7],归一化的灰度分布如下表所示:
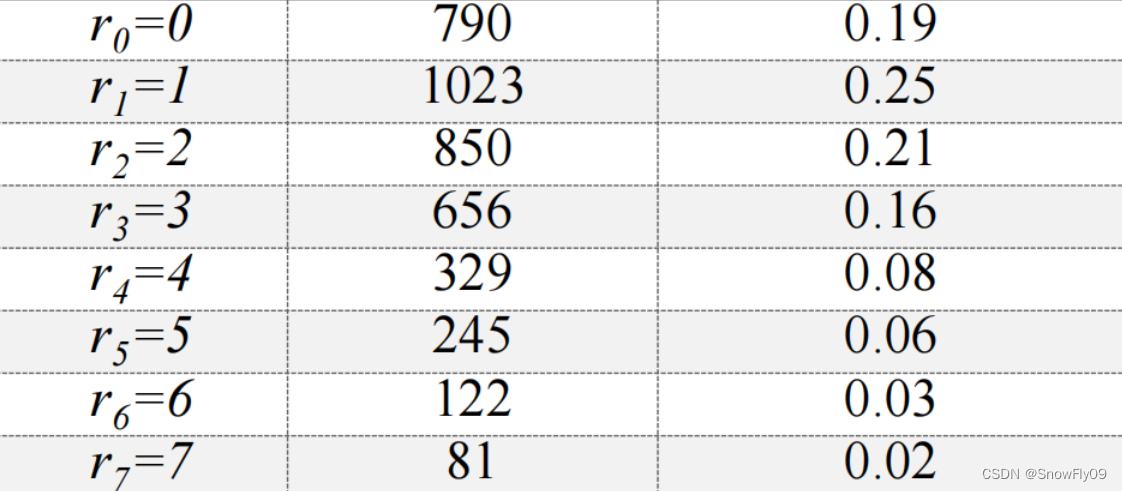
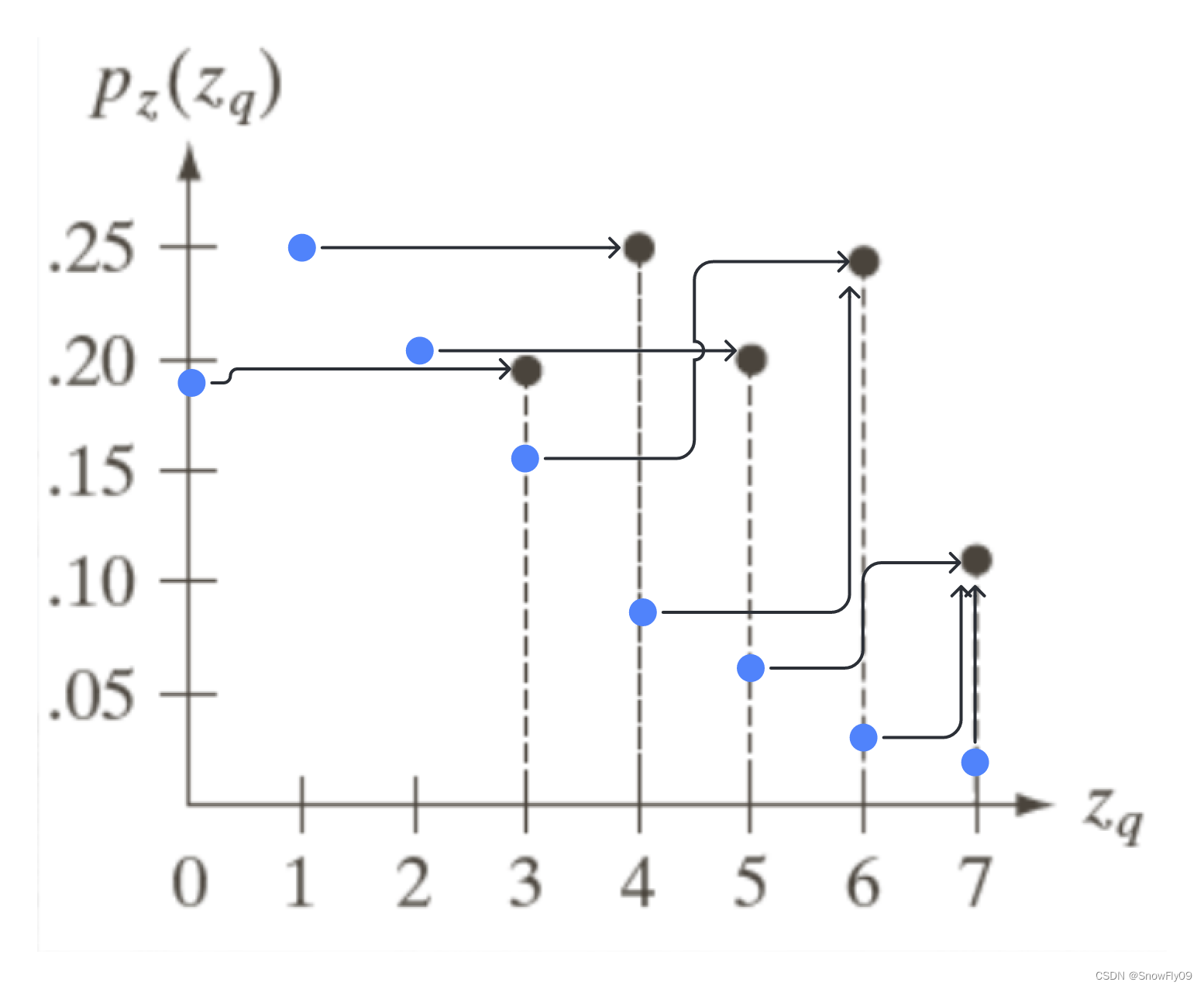
直方图均衡变换函数为: s k = T ( r k ) = ( L − 1 ) ∑ j = 0 k p r ( r j ) s_k = T(r_k)=(L-1)\sum\limits_{j=0}^kp_r(r_j) sk=T(rk)=(L−1)j=0∑kpr(rj)
可以计算得到: s 0 = 7 × p r ( r 0 ) = 7 ⋅ 0.19 = 1.33 s_0 = 7 \times p_r(r_0) = 7 \cdot 0.19 = 1.33 s0=7×pr(r0)=7⋅0.19=1.33, s 1 = 7 p r ( r 0 ) + 7 p r ( r 1 ) = 3.08 s_1= 7p_r(r_0) + 7p_r(r_1) = 3.08 s1=7pr(r0)+7pr(r1)=3.08,同样有s2=4.55,s3=5.67,s4=6.23,s5=6.65,s6=6.86,s7=7.00
将这些小数进行取整到最近的整数:
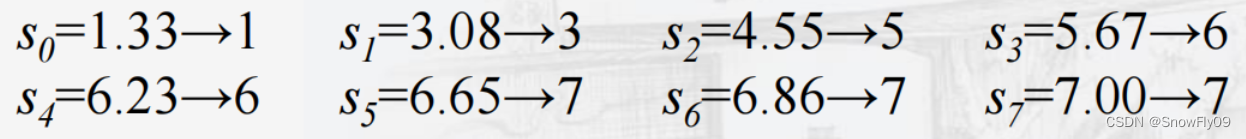
通过这一组式子,我们可以得到映射关系,原本灰度级为0的像素映射到1,灰度级为1的像素映射到3,其他类似
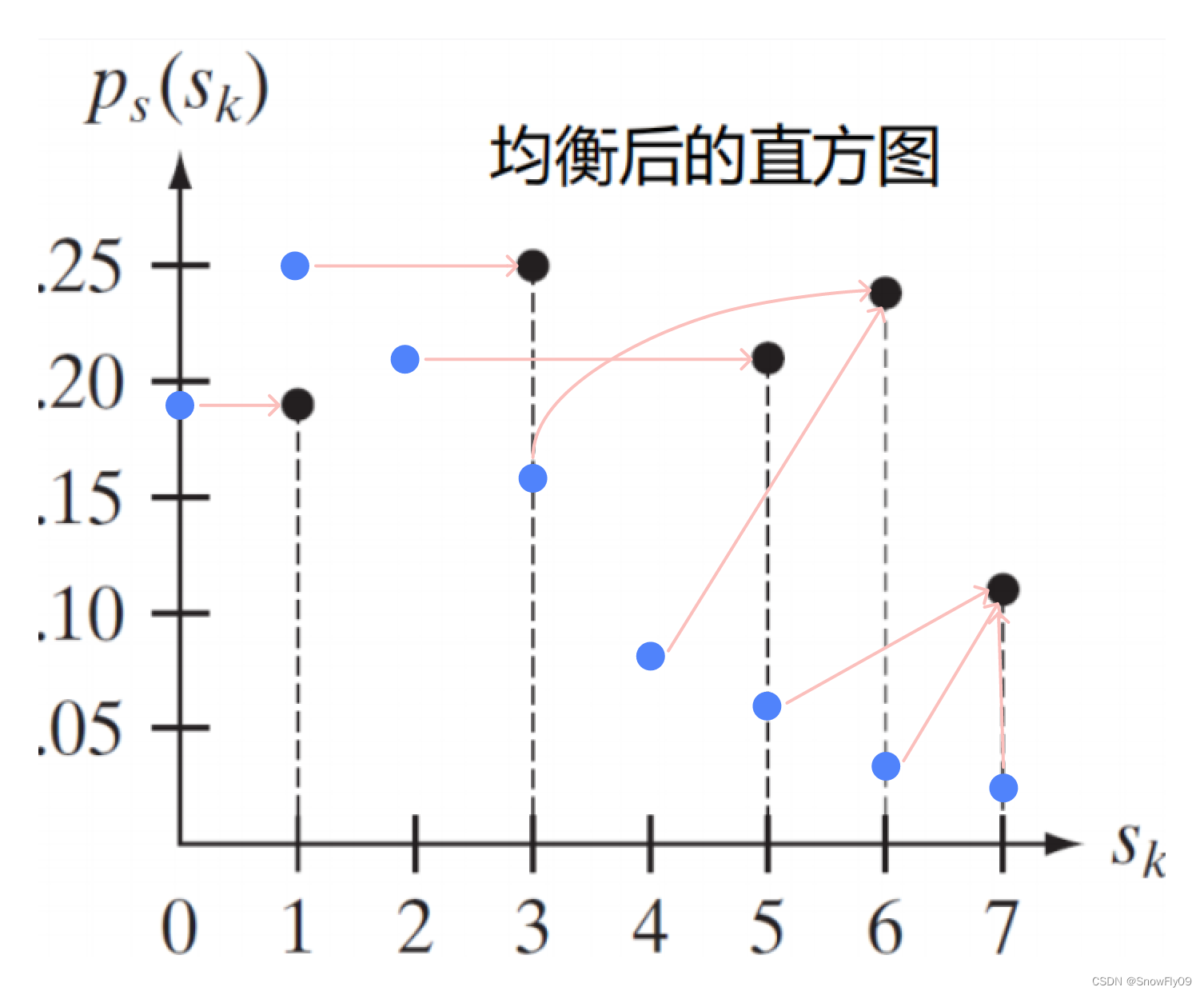
我们可以发现,均衡后的直方图在亮度上整体有了提高,同时尽可能均匀的平铺在所有灰度级中
直方图匹配
有时候直方图均衡处理完的图片并不满足我们需要的效果,比如对于上图我们只想提高亮度,而不想提高其对比度,那么通过直方图均衡这样的方法就没法做到。此时我们可以选取一张我们希望的亮度与对比度的图片,使用直方图匹配的方法来将原直方图变为我们需要的样子。
这里我们仍然忽略繁杂的理论推导,直接来看一看具体的例子,假设变换对象仍然为原来的图片,新的参考图的直方图给在了图中:
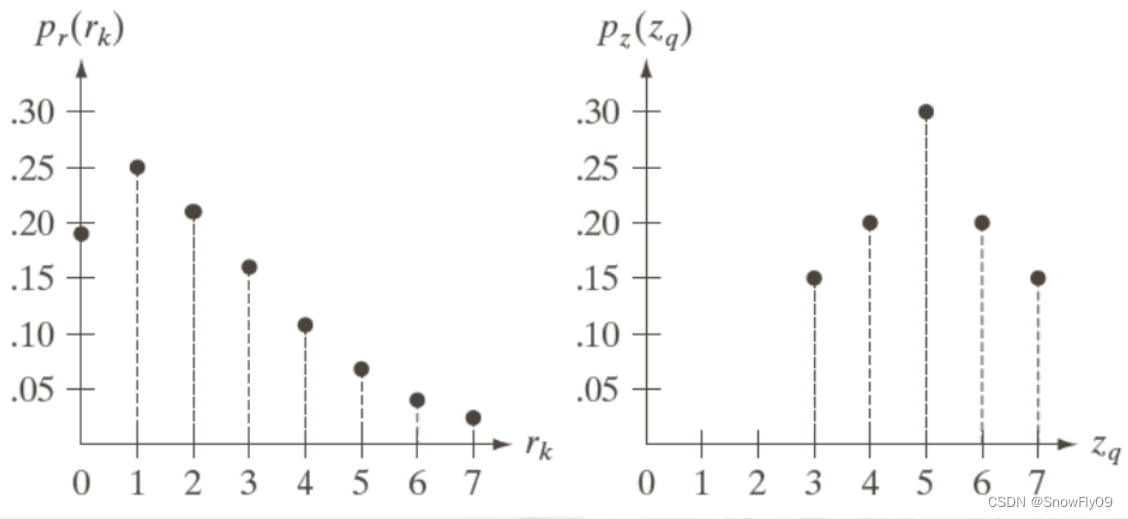
(1)对于原图与参考图均进行直方图均衡:
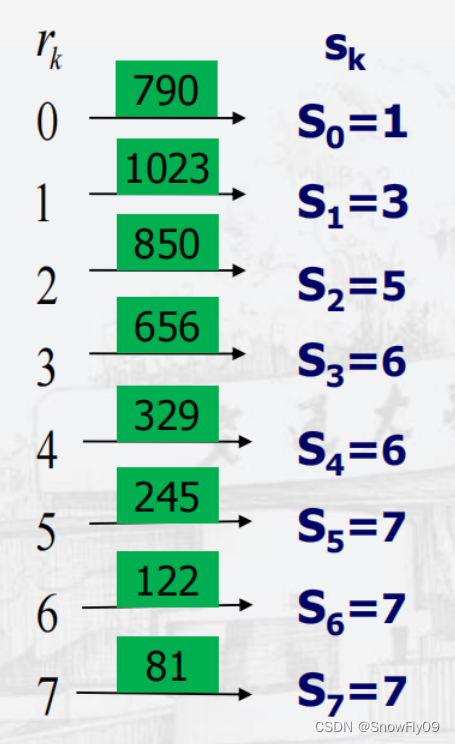
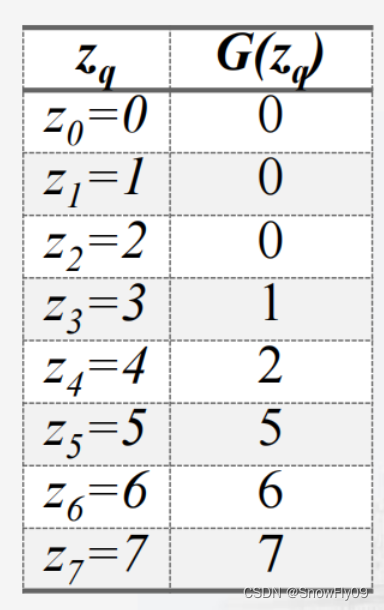
将s的值与G(z)的值相对应,每个s取最接近的G(z)值,当s离两个G(z)值一样接近时,取较小的那个,最终可以得到s对应z的映射,再加上原本r到s的映射,最终就能得到r到z的映射
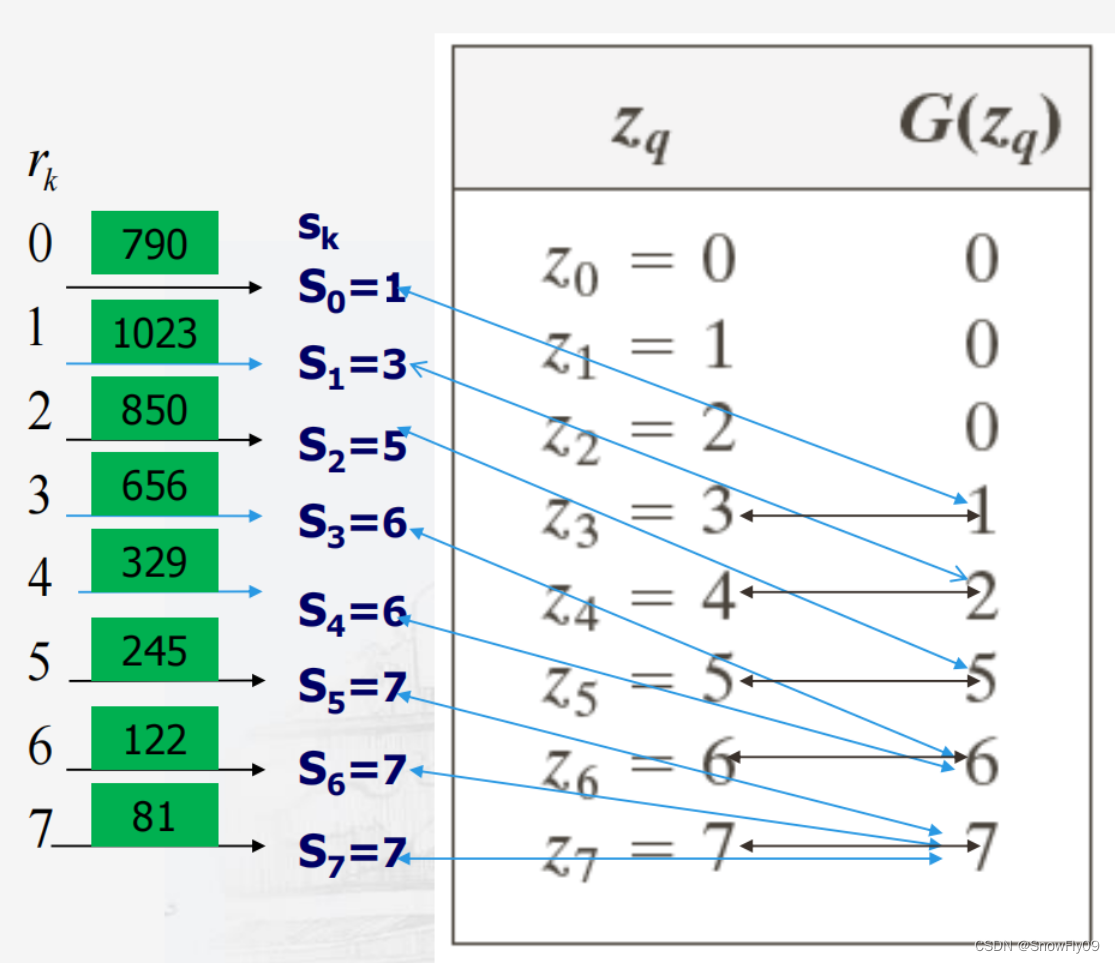
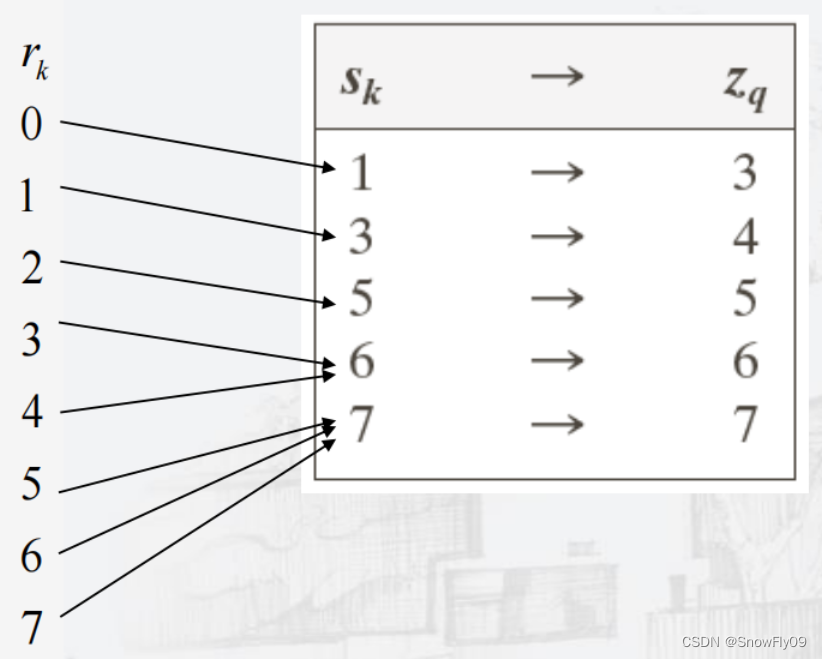
如此就可以得到目标的直方图,需要注意的是,映射完后原图的直方图各灰度级概率密度并不与目标图完全一致,而是指分布一致
空间滤波
滤波是指通过或拒绝一定范围内的频率分量,例如能够通过低频分量的滤波器叫做低通滤波器,最终效果可以对一幅图片进行模糊处理。
根据执行的操作可以分为:线性空间滤波器和非线性空间滤波器去
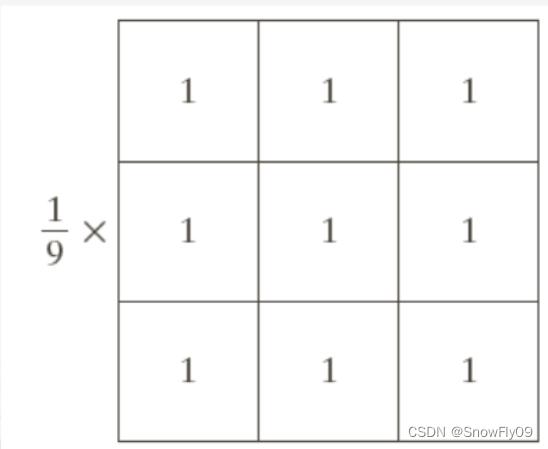
对于一个窗口为3x3的滤波器,其输出为各位置上的系数与对应像素值的乘积之和
如果期望图像中的像素变化为以该像素为中心的3x3邻域的平均灰度,可以使用 R = 1 9 ∑ i = 1 9 z i R = \frac{1}{9}\sum\limits_{i=1}^9z_i R=91i=1∑9zi
平滑空间滤波
平滑滤波用于模糊处理和降低噪声
模糊处理经常用于预处理任务,可以去除图像中的一些噪声
平滑线性滤波器
可以归入低通滤波器,主要作用是降低噪声,去除图像中的不相关细节,但也可能导致边缘模糊或者由于灰度级数量不足导致的伪轮廓
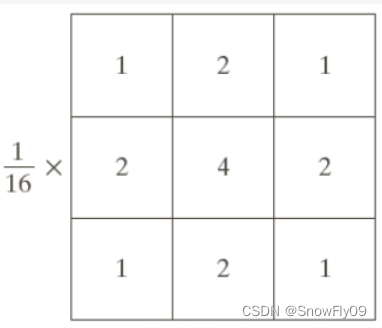
加权平均滤波:
非线性滤波器
统计排序滤波器是一种非线性滤波器,通过滤波器中包围的图像中所含像素的排序来决定中心像素的值
例如:中值滤波器,将滤波器内灰度的中值代替滤波器中心的值,此外除了取中值,还可以取最大值(最大值滤波器),最小值(最小值滤波器)
中值滤波器对于处理脉冲噪声(椒盐噪声)非常有效
锐化空间滤波器
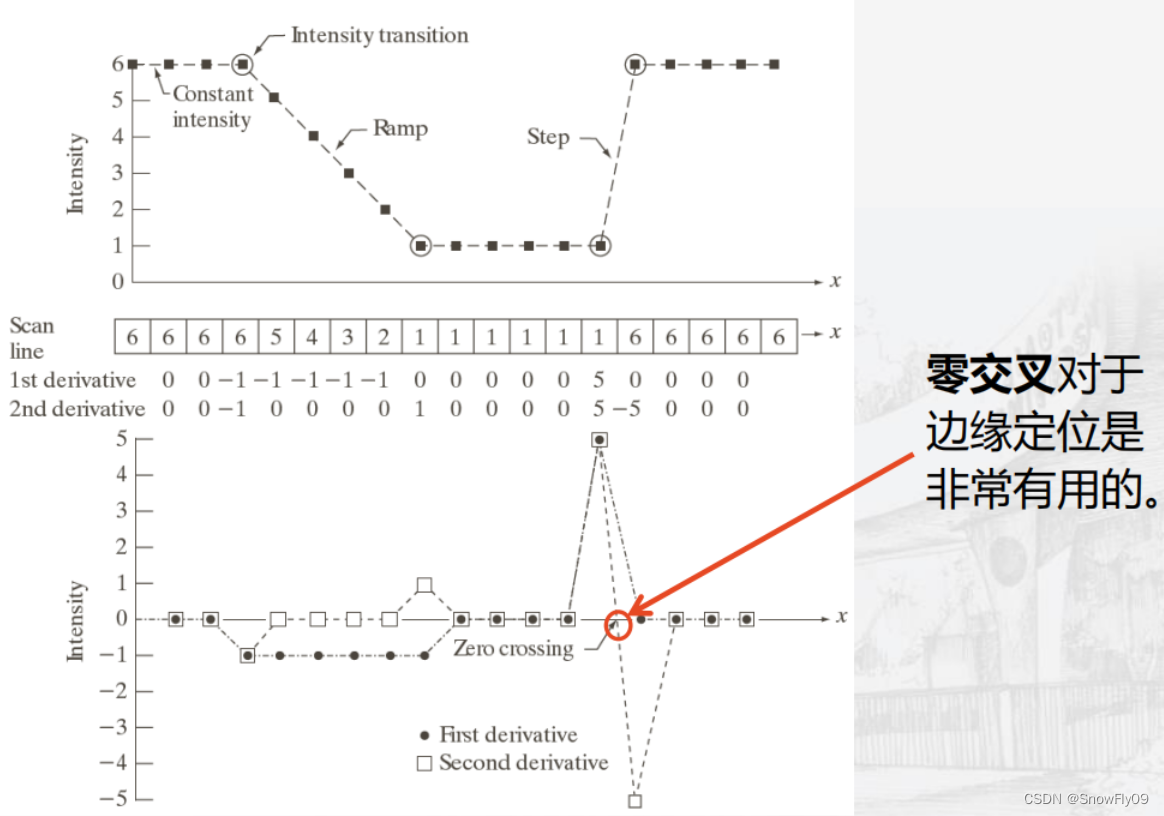
对于一阶微分和二阶微分的定义:
一阶微分:(1)在恒定区域为0(2)在斜坡或台阶的起点处非0(3)在斜坡上非0
二阶微分:(1)在恒定区域为0(2)在台阶或斜坡的起点处非0(3)在斜坡上为0
使用拉普拉斯算子进行图像锐化
拉普拉斯算子是一种各向同性微分算子,这种滤波器的响应与其以何方向作用在图像上无关。
对于两个变量的拉普拉斯算子,
∇ 2 f = ∂ 2 f ∂ x 2 + ∂ 2 f ∂ y 2 \nabla^2f=\frac{\partial^2f}{\partial x^2}+\frac{\partial^2f}{\partial y^2} ∇2f=∂x2∂2f+∂y2∂2f
将其以离散的形式表述,我们就可以得到:
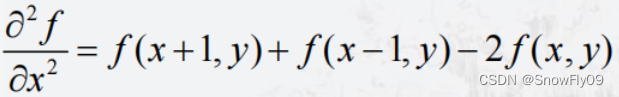
对于y也是同理:
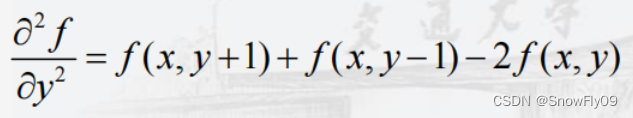
故最终可以得到:
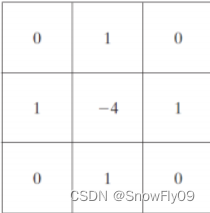
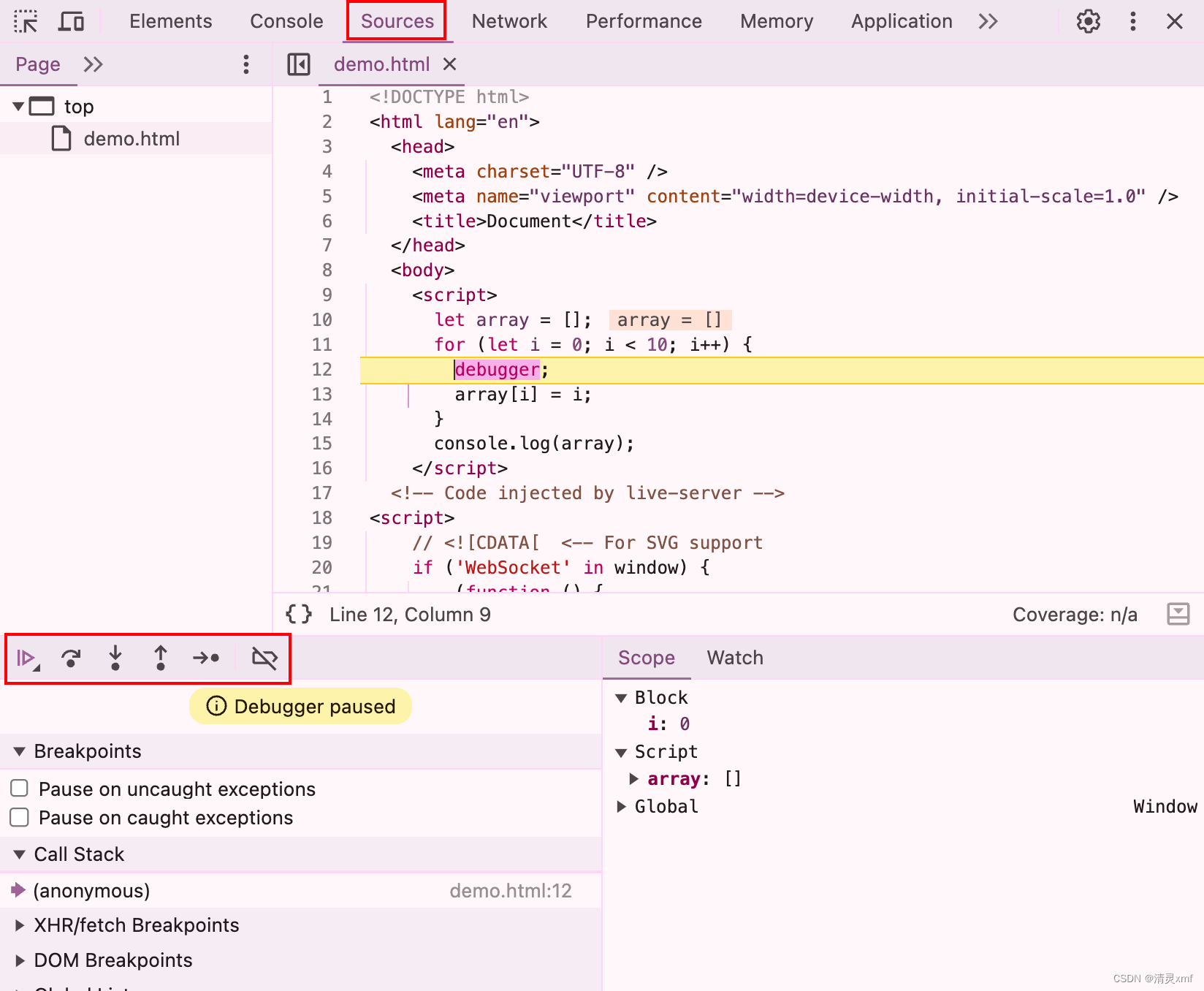
需要注意的是,拉普拉斯算子所产生的是一种滤波,可以认为是一种滤镜,和原图进行叠加才能起到相应的作用:

当拉普拉斯算子的中心常数为负时,c=-1,否则c=1




![[数据集][目标检测]旋风检测数据集VOC+YOLO格式157张1类别](https://img-blog.csdnimg.cn/direct/83778a7731d64af3bcf2e70a39acf8a0.png)

![[Windows] 植物大战僵尸杂交版](https://img-blog.csdnimg.cn/img_convert/079456a2ecbcdb04ca5a8ae9164f8ac7.jpeg)