贪婪是一种算法范式,它逐步构建解决方案,始终选择提供最明显和直接收益的下一个部分。贪婪算法用于解决优化问题。
如果问题具有以下属性,则可以使用贪心法解决优化问题:
每一步,我们都可以做出当前看来最好的选择,从而得到整个问题的最优解。
如果贪婪算法可以解决某个问题,那么它通常会成为解决该问题的最佳方法,因为贪婪算法通常比动态规划等其他技术更有效。但贪婪算法并不总是适用。例如,Fractional Knapsack问题可以使用Greedy来解决,但是0-1 Knapsack问题不能使用Greedy来解决。
以下是一些贪婪算法的标准算法:
1)Kruskal的最小生成树(MST):
在 Kruskal 算法中,我们通过一条一条地选取边来创建 MST。贪心选择是选择在目前构建的 MST 中不会引起循环的最小权重边
2)Prim的最小生成树:
在 Prim 的算法中,我们也是通过逐条选取边来创建 MST。我们维护两个集合:一组已包含在 MST 中的顶点和一组尚未包含的顶点。贪心选择是选择连接两个集合的最小权重边
3)Dijkstra的最短路径:
Dijkstra 算法与 Prim 算法非常相似。最短路径树是逐边构建的。我们维护两个集合:一组已包含在树中的顶点和一组尚未包含的顶点。贪心选择是选择连接两个集合并且位于从源到包含尚未包含的顶点的集合的最小权重路径上的边
4)霍夫曼编码:
霍夫曼编码是一种无损压缩技术。它将可变长度位代码分配给不同的字符。贪心选择是将最小位长的代码分配给最常见的字符。
贪心算法有时也用于获得硬优化问题的近似值。例如,旅行商问题是一个 NP 难问题。这个问题的贪婪选择是每一步都选择距离当前城市最近的未访问过的城市。这些解决方案并不总是产生最佳的最优解决方案,但可用于获得近似最优的解决方案。
这里让我们看一个可以使用贪心算法解决的问题
问题:
您将获得n项活动及其开始和结束时间。选择一个人可以执行的最大活动数,假设一个人一次只能从事一项活动。
例子:
输入: start[] = {10, 12, 20}, finish[] = {20, 25, 30}
输出: 0
解释:一个人最多可以执行一项活动。
输入: start[] = {1, 3, 0, 5, 8, 5}, finish[] = {2, 4, 6, 7, 9, 9};
输出: 0 1 3 4
解释:一个人最多可以执行四项活动。
可以执行的最大活动集 是
{0, 1, 3, 4} [ 这些是 start[] 和 finish[] 中的索引
方法:要解决该问题,请遵循以下想法:
贪心选择是总是选择剩余活动中完成时间最短的下一个活动,并且开始时间大于或等于先前选择的活动的结束时间。我们可以根据活动的完成时间对活动进行排序,以便我们始终将下一个活动视为完成时间最短的活动
请按照给定的步骤解决问题:
1、根据活动的完成时间对活动进行排序
2、从排序数组中选择第一个活动并打印它
3、对排序数组中的剩余活动执行以下操作
4、如果此活动的开始时间大于或等于先前选择的活动的结束时间,则选择此活动并打印
注意:在实现中,假设活动已经按照完成时间排序,否则时间复杂度将上升到 O(N*log(N)),辅助空间将上升到 O(N),因为我们必须创建一个二维数组来将开始时间和结束时间存储在一起。
下面是上述方法的实现。
# Python3 program for activity selection problem.
# The following implementation assumes that the activities
# are already sorted according to their finish time
# Prints a maximum set of activities that can be done
# by a single person, one at a time
def printMaxActivities(s, f):
n = len(f)
print("Following activities are selected")
# The first activity is always selected
i = 0
print(i, end=' ')
# Consider rest of the activities
for j in range(1, n):
# If this activity has start time greater than
# or equal to the finish time of previously
# selected activity, then select it
if s[j] >= f[i]:
print(j, end=' ')
i = j
# Driver code
if __name__ == '__main__':
s = [1, 3, 0, 5, 8, 5]
f = [2, 4, 6, 7, 9, 9]
# Function call
printMaxActivities(s, f)
# This code is contributed by Nikhil Kumar Singh
输出
选择以下活动
0 1 3 4
时间复杂度: O(N)
辅助空间: O(1)
贪婪选择如何适用于根据完成时间排序的活动?
假设给定的活动集为 S = {1, 2, 3, …n},活动按完成时间排序。贪婪选择总是选择活动 1。为什么活动 1 总是提供最佳解决方案之一?
我们可以通过证明如果存在另一个解 B 且第一个活动不是 1,则也存在一个与活动 1 大小相同的解 A 作为第一个活动。设B选择的第一个活动为k,则总存在A = {B – {k}} U {1}。
注: B 中的活动是独立的,并且 k 的完成时间是所有活动中最小的。由于 k 不为 1,所以 finish(k) >= finish(1))
当给定的活动未排序时如何实施?
我们为活动创建一个结构/类。我们按完成时间对所有活动进行排序(请参阅C++ STL 中的排序)。一旦我们对活动进行排序,我们就应用相同的算法。
下图是上述方法的说明:
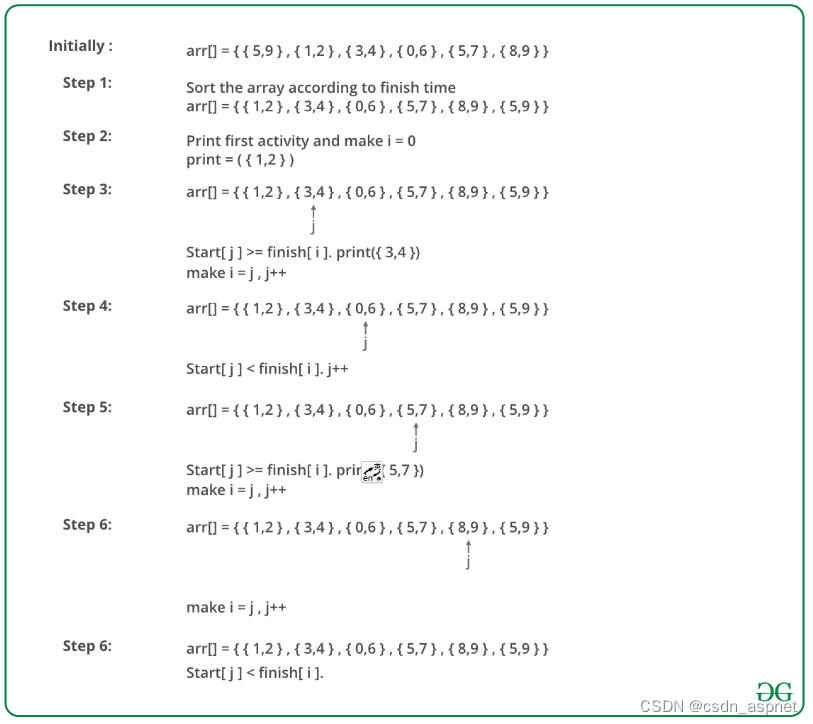
下面是上述方法的实现:
''' Python program for activity selection problem
when input activities may not be sorted.'''
def MaxActivities(arr, n):
selected = []
# Sort jobs according to finish time
Activity.sort(key=lambda x: x[1])
# The first activity always gets selected
i = 0
selected.append(arr[i])
for j in range(1, n):
'''If this activity has start time greater than or
equal to the finish time of previously selected
activity, then select it'''
if arr[j][0] >= arr[i][1]:
selected.append(arr[j])
i = j
return selected
# Driver code
if __name__ == '__main__':
Activity = [[5, 9], [1, 2], [3, 4], [0, 6], [5, 7], [8, 9]]
n = len(Activity)
# Function call
selected = MaxActivities(Activity, n)
print("Following activities are selected :")
print(selected[0], end = "");
for i in range (1, len(selected)):
print(",", end = " ")
print(selected[i], end = "")
# This code is contributed by kshitijjainm
输出
选定以下活动:
(1、2)、(3、4)、(5、7)、(8、9)
时间复杂度: O(N log N),如果输入活动可能无法排序。当输入活动始终排序时,需要 O(n) 时间。
辅助空间: O(1)
使用优先级队列的活动选择问题:
我们可以使用 Min-Heap 来获取完成时间最短的活动。Min-Heap 可以使用优先级队列实现
请按照给定的步骤解决问题:
1、创建优先级队列(最小堆)并将活动推入其中。
2、将优先级队列的顶部推入答案向量,并将变量start设置为第一个活动的开始时间,将变量end 3、设置为该活动的结束时间
4、当优先级不为空时,执行以下操作:
4.1、取出优先级队列的顶部并检查
4.2、如果此活动的开始时间大于或等于最后选择的活动的结束时间,则将此活动推入答案向量
4.3、不然就忽略它
5、打印选择的活动,存储在答案向量中
下面是上述方法的实现:
# Python3 program for activity selection problem
# when input activities may not be sorted.
from heapq import heappop, heappush
# Function to select activites
def SelectActivities(s, f):
ans = []
p = []
# Pushing elements in the list
for i, j in zip(s, f):
heappush(p, (j, i))
it = heappop(p)
start = it[1]
end = it[0]
ans.append(it)
# Sorting process
while p:
it = heappop(p)
if it[1] >= end:
start = it[1]
end = it[0]
ans.append(it)
print("Following Activities should be selected.\n")
for f, s in ans:
print(f"Activity started at {s} and ends at {f}")
# Driver code
if __name__ == "__main__":
s = [1, 3, 0, 5, 8, 5]
finish = [2, 4, 6, 7, 9, 9]
# Function call
SelectActivities(s, finish)
# This code is contributed by kraanzu.
输出
应选择以下活动。
活动开始于:1 结束于:2
活动开始于:3 结束于:4
活动开始于:5 结束于:7
活动开始于:8 结束于:9
时间复杂度: O(N * log N)
辅助空间: O(N)
![[数据集][目标检测]水下管道泄漏破损检测数据集VOC+YOLO格式2069张2类别](https://img-blog.csdnimg.cn/direct/96c965ba8e91425fb9c4b36043f09162.png)