拓扑排序详解

一、拓扑排序前置知识

1.1 定义：

1.2 AOV网：

二、如何拓扑排序

2.1 运用 kahn 算法：

2.2 实现拓扑排序：

2.3 拓扑排序的应用：

2.4 拓扑排序编写模板：

三、例题练习

3.1 例题1：课程表

3.2 例题2：课程表II

3.3 例题3：火星词典

四、时间复杂度分析及合理性证明

4.1 时间复杂度：

4.2 合理性证明：

一、拓扑排序前置知识

1.1 定义：

拓扑排序主要用来解决有向无环图（DAG 图）的所有节点的排序。简单来说就是找到做事情的先后顺序，拓扑排序的结果可能不是唯一的。

我们可以那我们日常上学的例子来描述这个过程，全部的步骤有【起床】、【洗漱】、【吃饭】、【穿衣服】、【整理书包】、【上学去】等，要想完成洗漱和穿衣服的后续操作就必须要先起床，起床后做洗漱和穿衣服都可以（拓扑排序的结果不唯一），最后上学的时候必须要把前面那 5 步都执行完毕才可以去上学。这就是拓扑排序的过程。

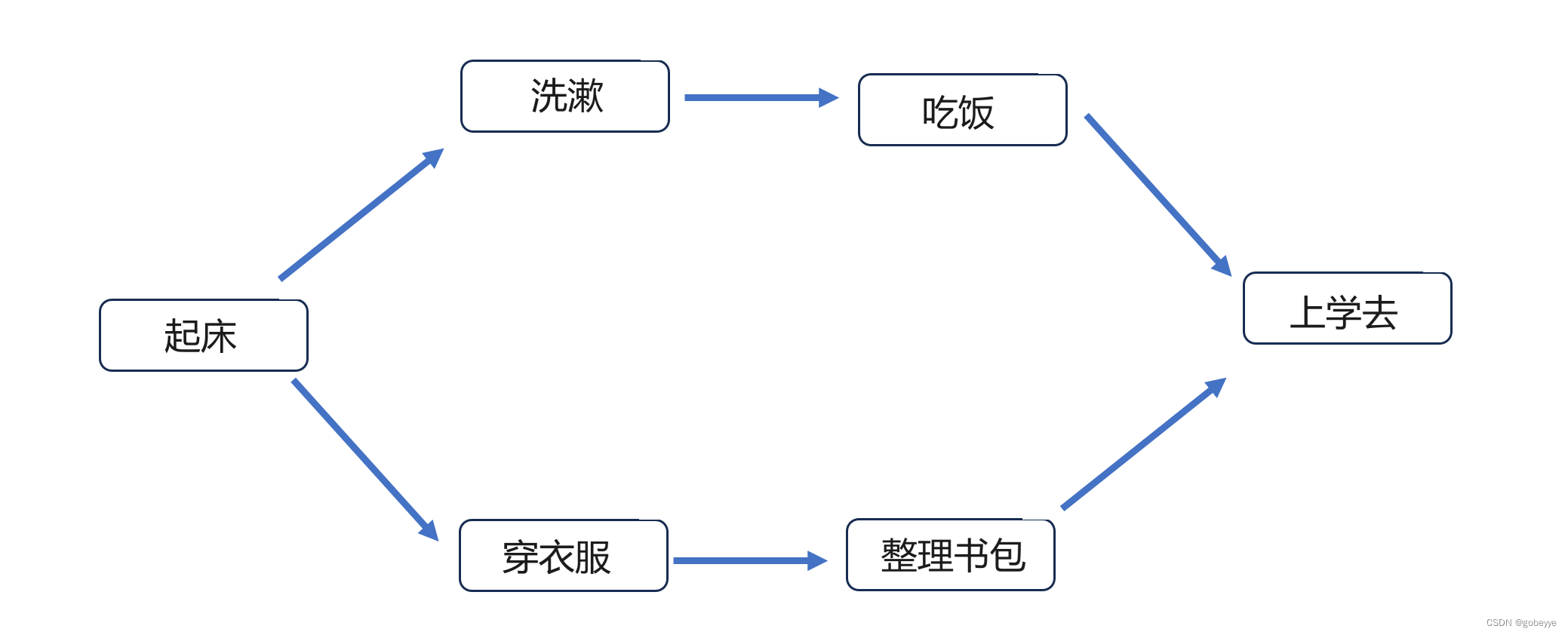
这里需要先了解什么是入度，什么是出度。

入度：是以 v 为终点的有向边的条数。

出度：是以 v 为起始点的有向边的条数。

1.2 AOV网：

AOV网：顶点活动图。在有向无环图中，用顶点来表示一个活动，用边来表示活动的先后顺序的图结构。

在日常生活中，我们进行的活动都可以看作是由若干个子活动组成的集合，这些活动之间必定存在一定的先后顺序，即某些子活动必须在其他的一些子活动完成后才能开始。

我们用有向图来表现子活动之间的先后关系，子活动之间的先后关系为有向边，这种有向图称为顶点活动网络，即 AOV 网（Activity On Vertex Network）。一个 AOV 网必定是一个有向无环图，即不带有回路。

二、如何拓扑排序

2.1 运用 kahn 算法：

没学过没关系，我们就是要讲这个。

• 过程：

初始状态下，集合 S装着所有入度为 0 的点，L 是一个空列表。

每次从 S 中取出一个点 u（可以随便取）放入 L, 然后将 u 的所有边 (u,v1),(u,v2),(u,v3)..... 删除。对于边 (u,v)，若将该边删除后点 v 的入度变为 0，则将 v 放入 S 中。

不断重复以上过程，直到集合 S 为空。检查图中是否存在任何边，如果有，那么这个图一定有环路，否则返回 L，L 中顶点的顺序就是构造拓扑序列的结果。

上面就是 kahn 算法是实现过程。下面为了减少友友的学习成本，我在下面给出在代码中我们具体要如何实现。

2.2 实现拓扑排序：

借助队列来一次 BFS 即可。

• 初始化：把所有入度为 0 的点加入到队列中。

• 当队列不为空的时候：

1. 拿出队头元素，加入到最终结果中。

2. 删除与该元素相连的边。

3. 判断：与删除边相连的点，是否入度变为 0 ，如果入度为 0 ，加入到队列中。

到这里有一个致命的问题：如何建图？如何在图上进行上述删除节点的操作？

我们要灵活的使用语言提供的容器（c 语言的话当我没说），建图无非就两种，一种是邻接矩阵，另一种是邻接表。拓扑排序采用邻接表会更加方便一些，我们可以使用 List<List<Integer>> edges（局部）；或者 Map<Integer,List<Integer>> edges（通用）; 完成建表。

最后我们使用一个 int 类型的数组来统计各个节点的入度。这里如果节点不是数字的话，我们要想办法把它转化成数字，例如如果节点是字符串的话，我们可以自己构造一个哈希函数，来把字符串转化成数字。

例如上图：

第一步删去入度为 0 点（【起床】）及其对应的边并将其加入到结果中，这样【洗漱】和【穿衣服】就成了入度为 0 的点。

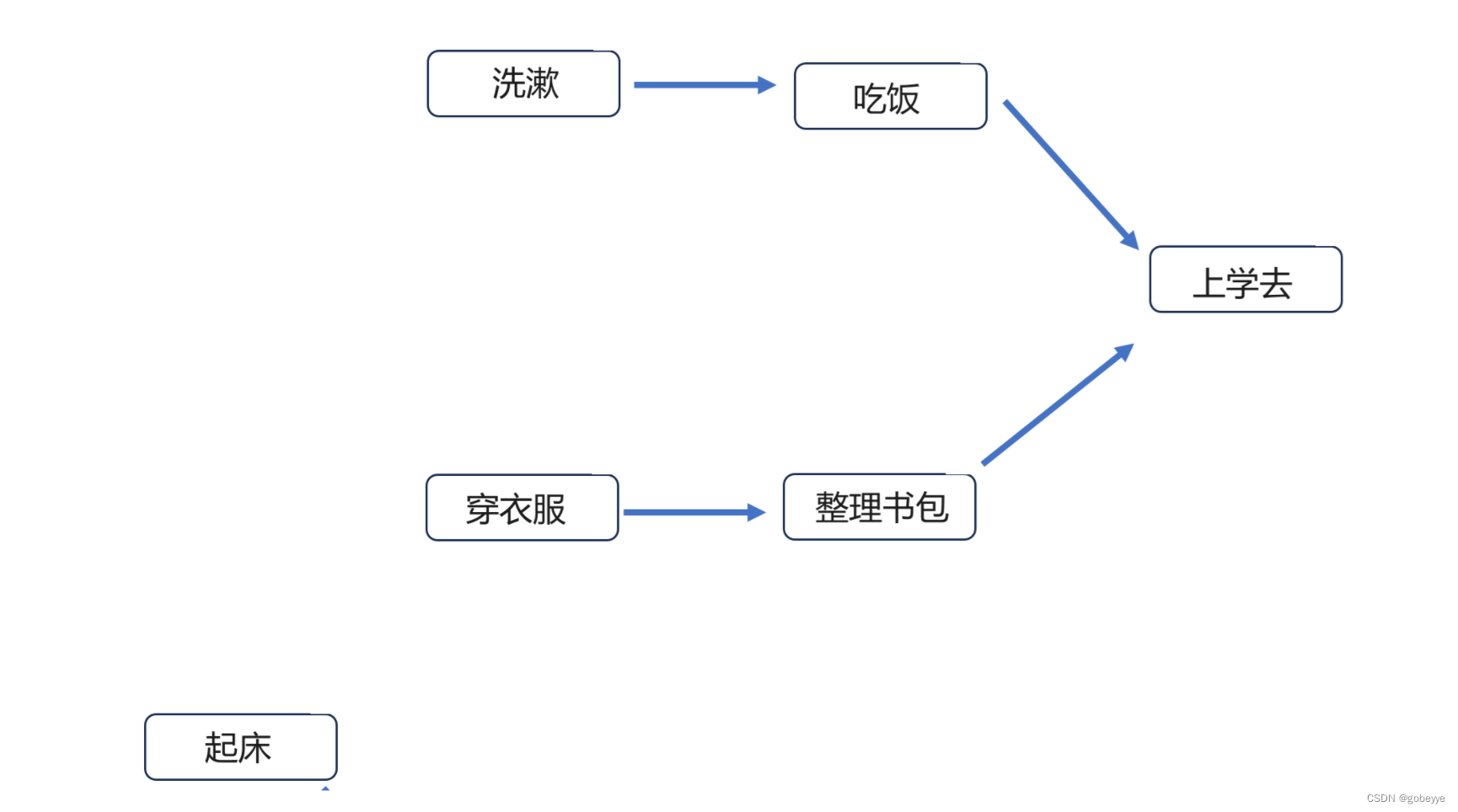
接着将【洗漱】和【穿衣服】入队，因为入度都为 0 所以谁先谁后都可以。

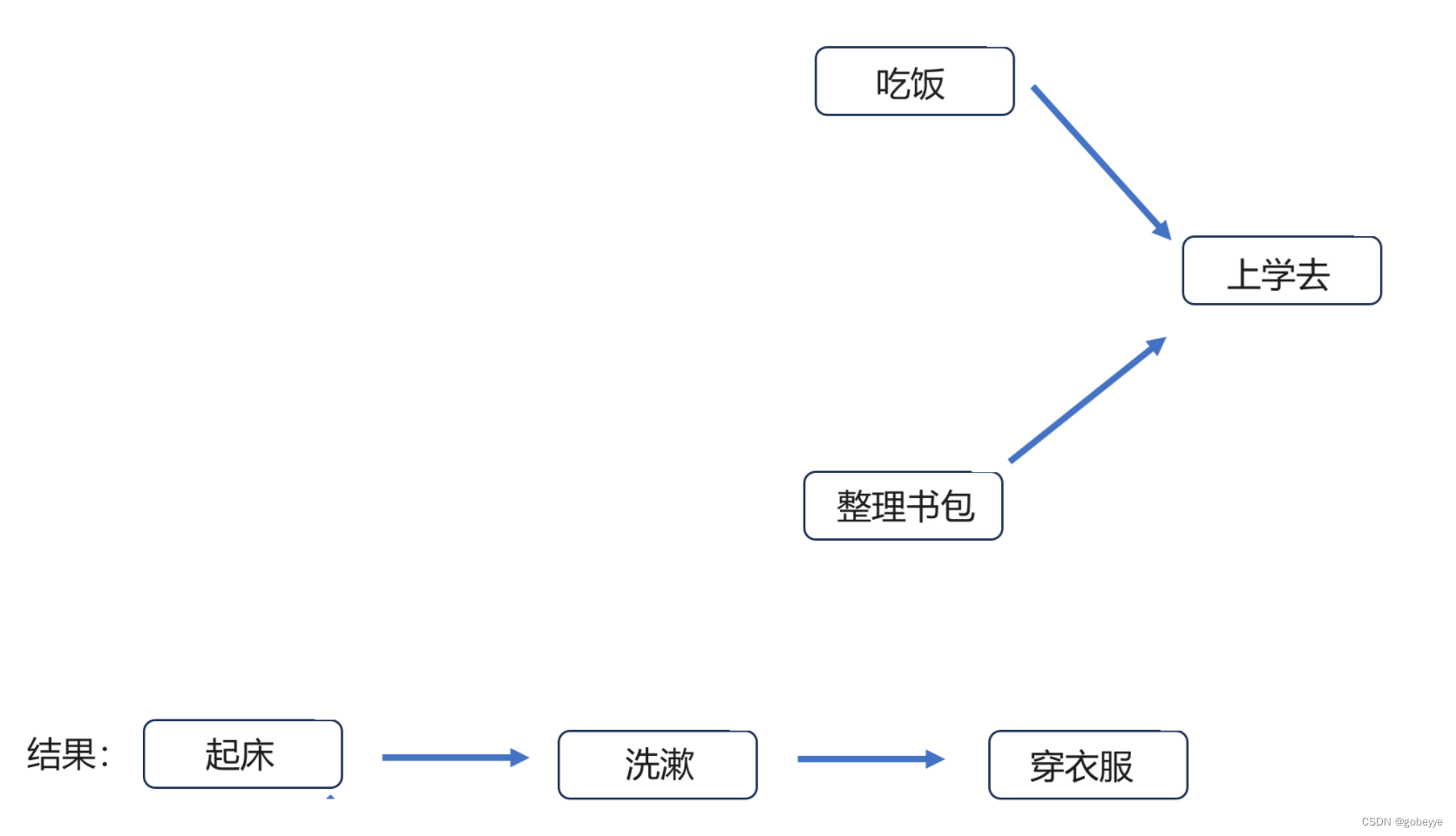
接着就是重复上面的操作，【上学去】必须是最后一个。

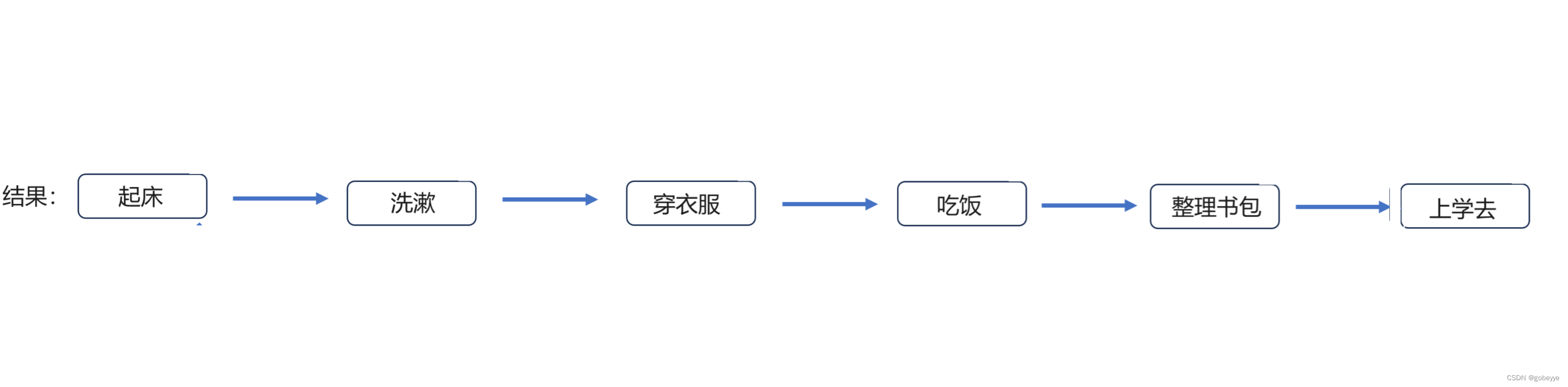
最后排序的结果如上图。

2.3 拓扑排序的应用：

拓扑排序可以用来判断有向图中是否有环。

2.4 拓扑排序编写模板：

拓扑排序：

1. 准备工作：

• 建立入度表。

• 建立edge（1.Map，2.List）。

2. 建表：

建表时入度要记得 ++ 。

3. 拓扑排序：

拓扑排序前要把入度为 0 的节点进入队列。

三、例题练习

说了那么多，我们来几题练练手。

3.1 例题1：课程表

• 题目链接：课程表

• 问题描述：

你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。

在选修某些课程之前需要一些先修课程。先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则必须先学习课程 bi 。

例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。

请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。

• 解题思路：

原问题可以转换成⼀个拓扑排序问题。用 BFS 解决拓扑排序即可。根据 2.4 的编写模板来编写代码，这是第一题，可以直接看，代码是如何实现的，拓扑排序其实也是很固定的那一套写法，写多了就觉得就那样啦。

• 代码编写：

class Solution {public boolean canFinish(int n, int[][] p) {//1.准备工作int[] in = new int[n];//存储入度Map<Integer,List<Integer>> edges = new HashMap<>();//存储边//2.建图for(int[] tmp:p){int a = tmp[0],b = tmp[1];if(!edges.containsKey(b)){edges.put(b,new ArrayList<>());//建立边的关系}edges.get(b).add(a);//一个点不止只有一条边in[a]++;}//3.拓扑排序Queue<Integer> q = new LinkedList<>();for(int i = 0;i < n;i++){if(in[i] == 0){q.add(i);}}while(!q.isEmpty()){int t = q.poll();for(int x:edges.getOrDefault(t,new ArrayList<>())){in[x]--;if(in[x] == 0){//入度为 0 进入队列q.add(x);}}}//4.判环for(int x:in){//如果有的节点入度不为 0 说明有环if(x != 0){return false;}}return true;}
}

3.2 例题2：课程表II

• 题目链接：课程表II

• 问题描述：

现在你总共有 numCourses 门课需要选，记为 0 到 numCourses - 1。给你一个数组 prerequisites ，其中 prerequisites[i] = [ai, bi] ，表示在选修课程 ai 前必须先选修 bi 。

例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示：[0,1] 。

返回你为了学完所有课程所安排的学习顺序。可能会有多个正确的顺序，你只要返回 任意一种 就可以了。如果不可能完成所有课程，返回 一个空数组 。

• 解题思路：

和上面的课程表1基本一模一样，可以拿这题练练手，唯一区别就是要把遍历结果，存储下来。

下面的代码编写是用 List<List<Integer>> 来编写的，没有什么特别的好处，主要是想给友友们展示一下两种写法。

• 代码编写：

class Solution {public int[] findOrder(int n, int[][] p) {//拓扑排序//1.准备int[] in = new int[n];//入度int[] ans = new int[n];//最后的答案int k = 0;List<List<Integer>> edges = new ArrayList<>();for(int i = 0;i < n;i++){edges.add(new ArrayList<>());//这里必须要先创建，下标必须要从0到n，这一点其实我不是很喜欢}//2.建表for(int i = 0;i < p.length;i++){int a = p[i][0],b = p[i][1];//如果 b 不存在开辟一个edges.get(b).add(a);in[a]++;//注意对应入度要增加}//3.拓扑排序Queue<Integer> q = new LinkedList<>();for(int i = 0;i < n;i++){if(in[i] == 0){q.add(i);//入的是下标，所以不能使用foreach}}while(!q.isEmpty()){int t = q.poll();ans[k++] = t;for(int x:edges.get(t)){in[x]--;if(in[x] == 0){q.add(x);}}}return n == k ? ans : new int[0];}
}

稍微上点强度。

3.3 例题3：火星词典

• 题目链接：火星词典

• 问题描述：

现有一种使用英语字母的外星文语言，这门语言的字母顺序与英语顺序不同。

给定一个字符串列表 words ，作为这门语言的词典，words 中的字符串已经 按这门新语言的字母顺序进行了排序 。

请你根据该词典还原出此语言中已知的字母顺序，并 按字母递增顺序 排列。若不存在合法字母顺序，返回 "" 。若存在多种可能的合法字母顺序，返回其中 任意一种 顺序即可。

字符串 s 字典顺序小于 字符串 t 有两种情况：

在第一个不同字母处，如果 s 中的字母在这门外星语言的字母顺序中位于 t 中字母之前，那么 s 的字典顺序小于 t 。
如果前面 min(s.length, t.length) 字母都相同，那么 s.length < t.length 时，s 的字典顺序也小于 t 。

• 解题思路：

本题的难点在于题意的理解和如何收集信息（如何建图），我们可以使用两层 for 循环枚举出所有的两个字符串的组合，然后利用双指针，根据字典序规则找出信息。in 这里采用 Map 数据结构来存储，注意一定要初始化，不然就不会存在入度为 0 的节点，edges 里面的 value 要使用 Set 来去重，拓扑排序有重复的边，会出错的。

注意：本题有个非常恶心的地方，题目给出的条件有可能是错误的，但是题目没有说明，如果发现条件是错误的话直接返回空串即可。

• 代码编写：

class Solution {public static String alienOrder(String[] words) {//拓扑排序//1.准备工作int n = words.length;Map<Character,Integer> in = new HashMap<>();//记录入度，必须要初始化，不然就没有入度为 0 的节点for(int i = 0;i < words.length;i++){for(int j = 0;j < words[i].length();j++){in.put(words[i].charAt(j),0);//初始化入度点}}Map<Character,Set<Character>> edges = new HashMap<>();//使用 Set 去重StringBuilder sd = new StringBuilder();//2.建表for(int i = 0;i < n;i++){for(int j = i + 1;j < n;j++){char[] a = words[i].toCharArray();char[] b = words[j].toCharArray();int k = 0;for(k = 0;k < a.length && k < b.length;k++){if(a[k] != b[k]){if(!edges.containsKey(a[k])){edges.put(a[k],new HashSet<>());//a 是在前面的节点}if(!edges.get(a[k]).contains(b[k])){edges.get(a[k]).add(b[k]);//建表in.put(b[k],in.get(b[k]) + 1);//入度}break;//只要第一个不能的字母}}if(k == a.length || k == b.length){if(a.length > b.length){//这里非常恶心，因为能走到这里说明，前面的//字母都相等，谁长谁大，if的这种情况 a 长，理应 a 大，但是 a 排在//前面说明题目给出的字符串是错误的直接返回空字符串。（题目没有说明//给出的条件存在不合法，所以这里我错了很多次）return "";}}}}//3.拓扑排序Queue<Character> q = new LinkedList<>();for(Map.Entry<Character,Integer> entry:in.entrySet()){// mapif(entry.getValue() == 0){q.add(entry.getKey());}}//正常的拓扑排序，无非就是数字变成了字符而已。while(!q.isEmpty()){Character tmp = q.poll();sd.append(tmp);for(Character x:edges.getOrDefault(tmp,new HashSet<>())){in.put(x,in.get(x) - 1);if(in.get(x) == 0){q.add(x);}}}//最后要判断有没有环for(char ch:in.keySet()){if(in.get(ch) != 0){return "";}}String ans = sd.toString();return ans;}
}