文章目录
- 概念
- DoF(Degrees of Freedom)
- 复用增益(Multiplexing Gain)
- 自由度(Degrees of Freedom, DoF)
- 两者的关系
- 实际应用
- 关系总结
- 具体关系
- 例子
- 结论
- 近场MIMO的分集与复用与远场MIMO有何不同
概念
在通信领域,分集增益和复用增益是多天线技术(如MIMO)中的两个重要概念。它们分别是:
-
分集增益(Diversity Gain):
- 分集增益是通过利用多条独立信道来增强信号的可靠性和稳定性的一种增益。它通过在多个天线上发送相同的信息,使得接收端可以从多个独立的路径中接收信号,从而减少因单个路径衰落导致的信号丢失。这种方法可以显著提高信号的抗衰落能力,降低误码率,增强通信的可靠性。
-
复用增益(Multiplexing Gain):
- 复用增益是通过利用多条独立信道来增加系统的传输速率的一种增益。它通过在多个天线上发送不同的信息,使得接收端可以同时接收多个独立的信号,从而实现并行传输,增加系统的吞吐量。这种方法可以显著提高系统的频谱效率和传输速率,但对信道条件的要求较高。
这两个增益在MIMO系统中常常需要权衡和取舍。**高分集增益意味着更可靠的通信,但可能会牺牲一些传输速率;而高复用增益则意味着更高的传输速率,但可能会降低通信的可靠性。**因此,设计MIMO系统时需要根据具体应用的需求,在分集增益和复用增益之间找到一个平衡点。
分集和复用可以利用不同的域:空、时、频、功率、码。
DoF(Degrees of Freedom)
在无线通信中,天线的复用增益(Multiplexing Gain)和自由度(Degrees of Freedom, DoF)密切相关。理解它们的关系有助于更好地优化MIMO(多输入多输出)系统的性能。以下是两者的关系和定义:
复用增益(Multiplexing Gain)
复用增益是指通过利用多个天线在同一频率资源上同时传输多个独立数据流,从而增加系统的传输速率。复用增益的实现依赖于多天线系统中空间复用的能力。其优势在于可以显著提高系统的频谱效率。
自由度(Degrees of Freedom, DoF)
自由度指的是一个MIMO系统中可以独立传输的数据流的最大数量。具体来说,DoF表示系统能够支持的独立信道的数量,这些独立信道可以在同一时间、频率资源上同时进行传输。
两者的关系
在一个具有 ( N t N_t Nt ) 个发送天线和 ( N r N_r Nr ) 个接收天线的远场MIMO系统中,复用增益和自由度之间存在直接的关系。通常情况下,该系统的DoF可以表示为:
[ DoF = min ( N t , N r ) \text{DoF} = \min(N_t, N_r) DoF=min(Nt,Nr) ]
这意味着MIMO系统的复用增益上限由发送天线和接收天线中较少的一方决定。举例来说:
- 如果一个系统有4个发送天线和4个接收天线,则该系统的DoF为4,可以同时传输4个独立的数据流。
- 如果一个系统有2个发送天线和3个接收天线,则该系统的DoF为2,可以同时传输2个独立的数据流。
实际应用
在实际应用中,DoF不仅影响复用增益,还影响系统的总体性能。在理想条件下(如无噪声和无干扰),系统可以实现其最大DoF,从而获得最大的复用增益。然而,在实际环境中,信道条件、干扰、噪声等因素可能会影响系统的实际DoF,从而影响复用增益。
总结来说,天线的复用增益和自由度密切相关。自由度决定了系统可以同时传输的独立数据流的最大数量,从而直接影响复用增益的大小。因此,理解和优化系统的自由度是实现高复用增益的关键。
自由度(Degrees of Freedom, DoF)可以被视为复用增益(Multiplexing Gain)的一个指标。
关系总结
-
复用增益(Multiplexing Gain):
- 复用增益指的是系统通过空间复用多个独立的数据流而增加的传输速率。
- 复用增益衡量了系统的频谱效率和数据传输能力。
-
自由度(Degrees of Freedom, DoF):
- 自由度表示一个MIMO系统中能够独立传输的数据流的最大数量。
- DoF是系统能够支持的独立空间信道的数量。
具体关系
- 在一个具有 ( N t N_t Nt ) 个发送天线和 ( N r N_r Nr ) 个接收天线的MIMO系统中,自由度的最大值为 ( min ( N t , N r ) \min(N_t, N_r) min(Nt,Nr) )。
- 自由度直接决定了系统可以实现的最大复用增益。也就是说,如果系统的自由度是 ( k k k ),那么理论上系统可以实现的最大复用增益也是 ( k k k ) 个独立的数据流。
例子
-
理想情况下:
- 一个系统有4个发送天线和4个接收天线。自由度为4,意味着系统可以同时传输4个独立的数据流,复用增益也是4。
- 一个系统有2个发送天线和3个接收天线。自由度为2,意味着系统可以同时传输2个独立的数据流,复用增益也是2。
-
非理想情况下:
- 由于实际的信道条件(如干扰、噪声、多径效应等),系统可能无法实现理论上的最大自由度。实际的复用增益可能会低于理论上的自由度。
结论
自由度(DoF)可以看作是复用增益的一个理论上限或指标,指示了系统在理想条件下能够支持的独立数据流的最大数量。复用增益依赖于系统的自由度,实际应用中,通过优化系统设计和信道条件,可以尽可能接近这个理论上限,从而实现高效的数据传输。
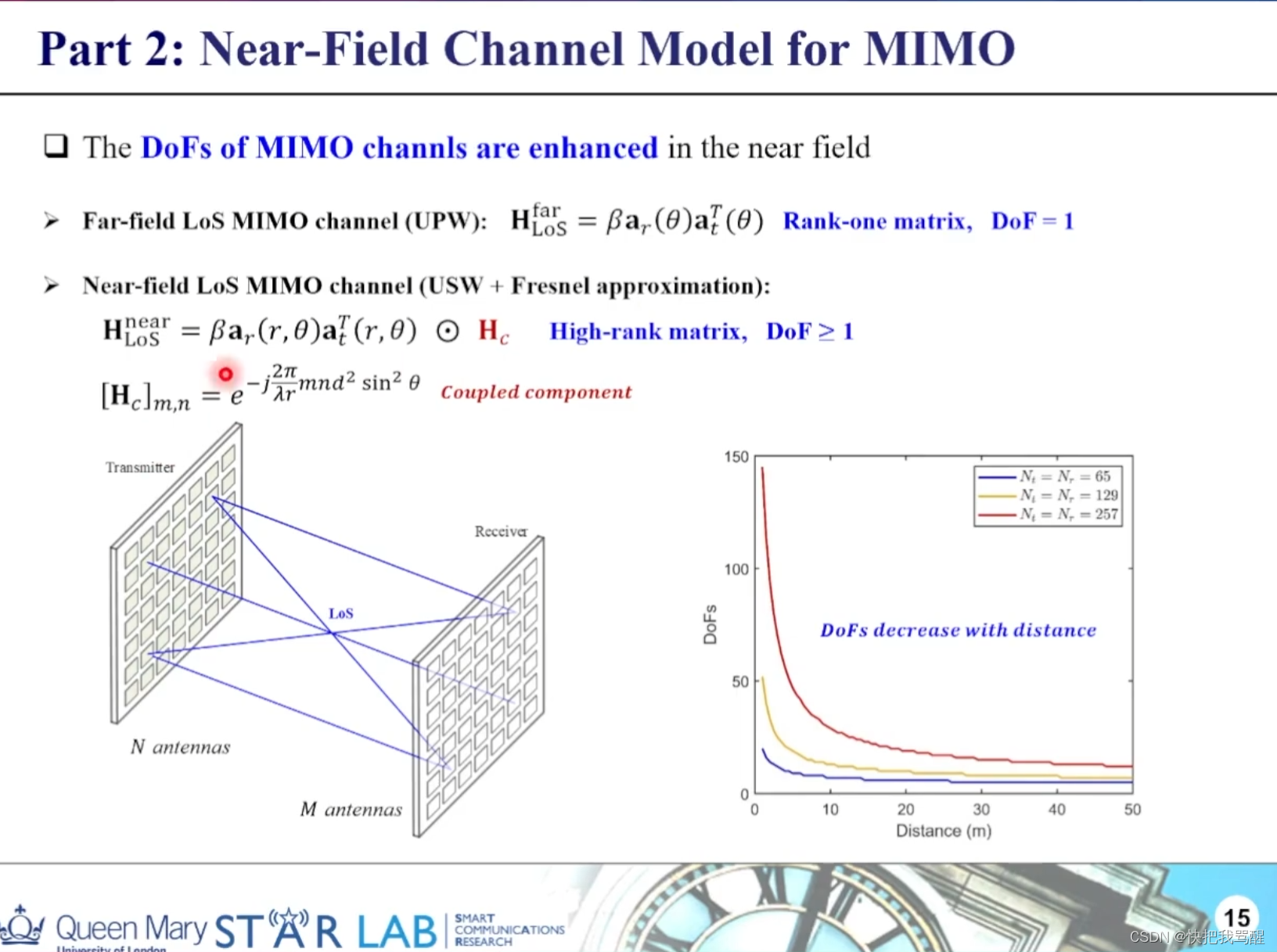
近场MIMO的分集与复用与远场MIMO有何不同
The DoFs of near-field LoS MIMO channel is distance-dependent.