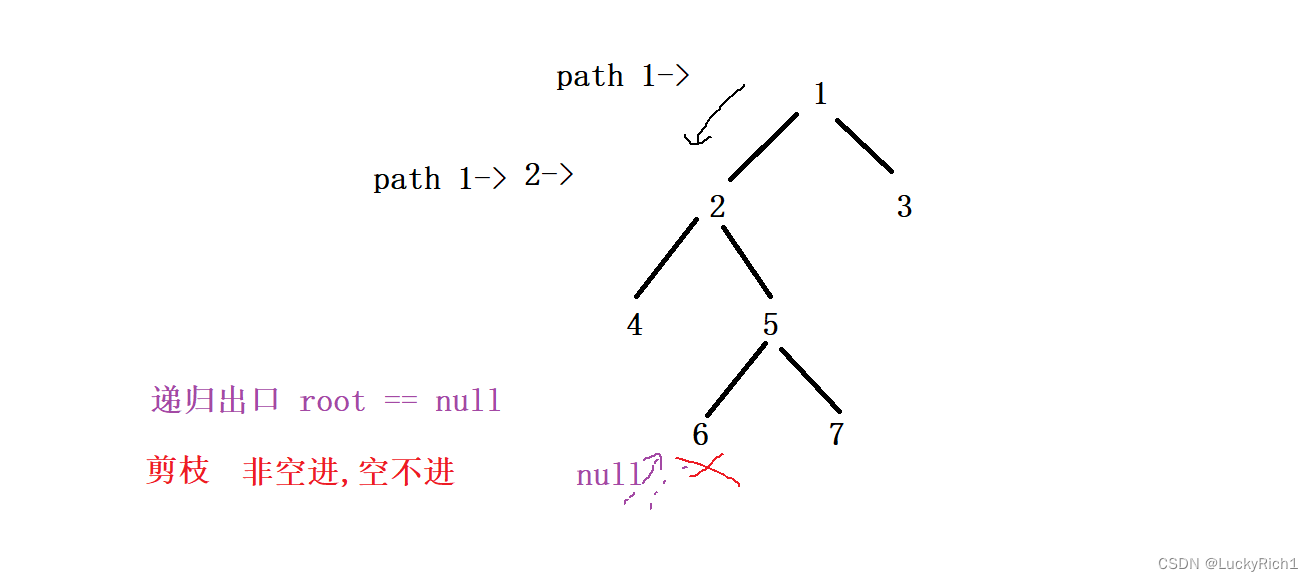
LLM过去有两种突破性技术大大提升了量化精度,分别是group-wise量化和GPTQ/AWQ量化。前者相比于过去的per-tensor和per-channel/per-axis量化提出了更细粒度的对channel拆分为更小单元的量化方式,后者通过巧妙的算法明显提升了4bit量化的精度。
LLM量化存在一个常识性的挑战是激活部分channel里面存在显著大于其他channel的异常值,这显著提升了激活量化的难度,并且对权重量化精度损失也有很大影响。一种以SliceGpt, QuaRot等为代表的新的方法可能改善这个局面,在近期成为一个研究热点。
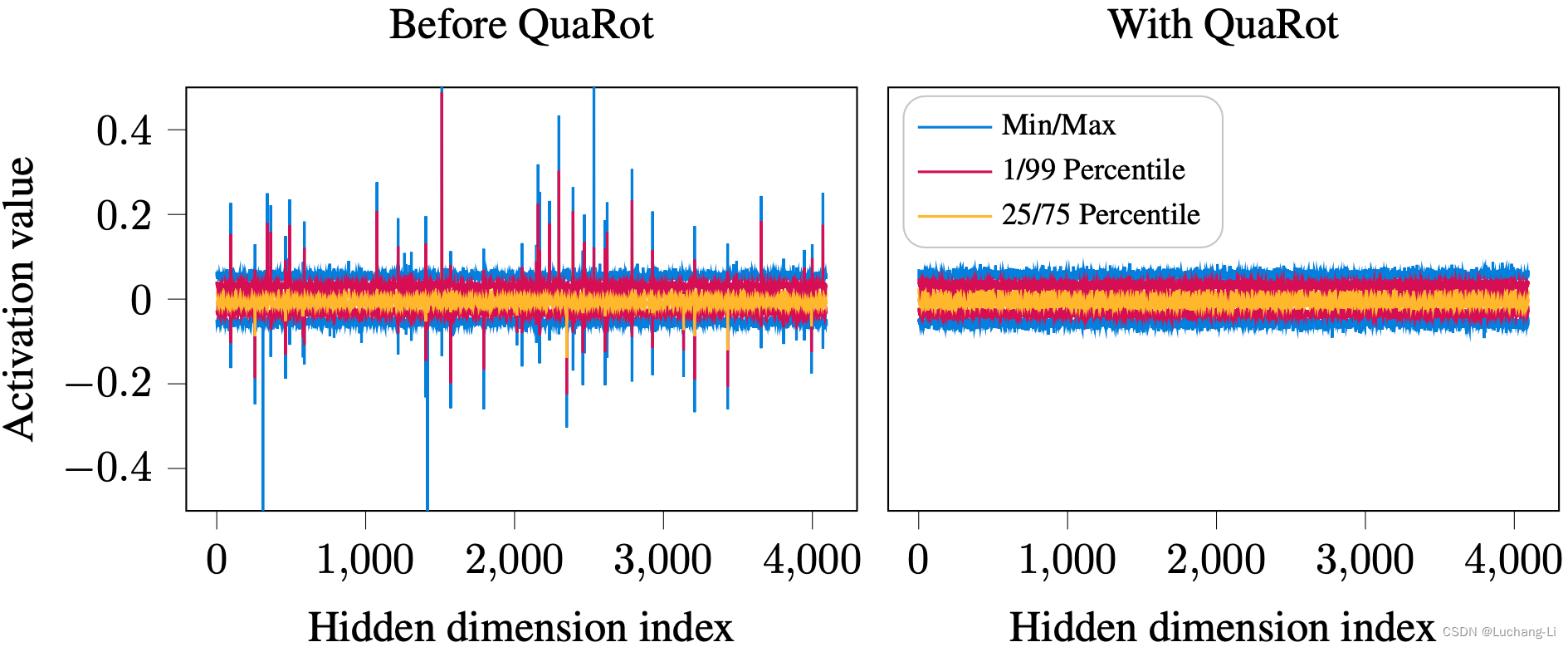
LLM激活量化outliers
LLM量化一个常识性的挑战是激活部分channel里面存在显著大于其他channel的异常值。
outlier存在于矩阵乘内积的K维度中。虽然理论上可以通过对不同channel采用不同的量化系数来解决这个问题, 但是模型量化一般对整个K是采用一个统一的量化系数,因为计算实现比较简单,而如果对K维度的每个元素用不同量化系数,那么矩阵乘时要进行非常频繁的反量化使得整个K维度所有元素共用同一套量化系数,结果才能累加在一起,因此对性能的损失肯定是异常显著的。也就是无法对单独的outlier channel跟其他channel使用不同量化系数来解决这个问题。
激活量化常用的的per-tensor或者per-token量化都无法解决这个问题。激活也采用权重的group量化可以部分解决这个问题,但是除CPU/GPU以外的其他硬件并不能很好地支持该量化方式。
过往的部分解决方案
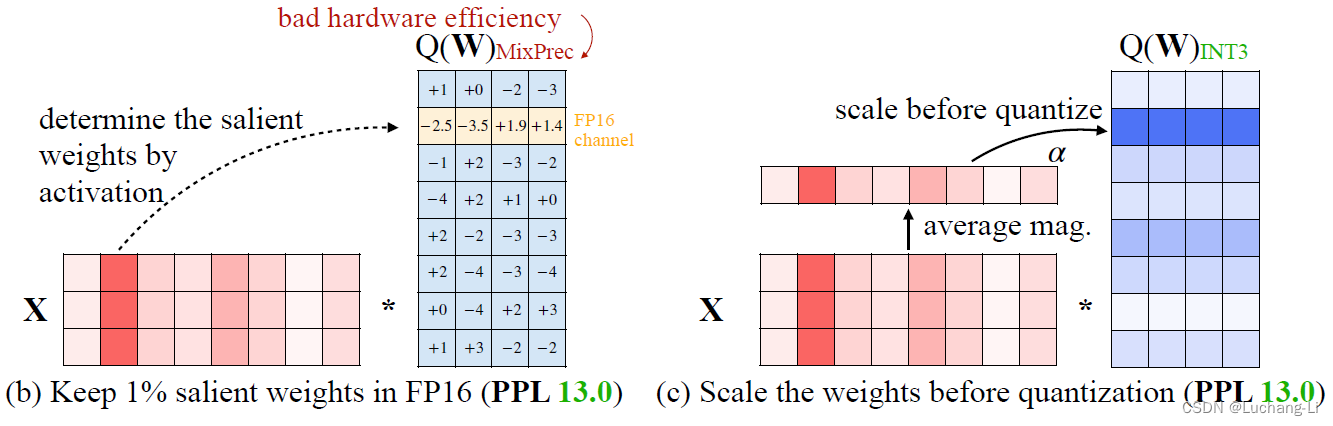
smooth quant通过scale向量,激活除以scale,权重乘以scale从而降低激活outlier幅度,把激活难度迁移到权重。
awq的思路跟smooth quant基本一致,都是韩松团队提出的。也是基于scale向量,激活除以scale,权重乘以scale。权重乘以scale进行放大后,可以降低放大部分的元素量化精度损失。
atom量化,对outlier通道部分的元素通过reorder后,与其他非outlier部分区别对待,outlier部分通道采用高精度计算。
IntactKV: Improving Large Language Model Quantization by Keeping Pivot Tokens Intact,提出了一种非常简单的方法来保护prompt开头部分的公共前缀的kv cache,从而避免特殊token引入的outlier精度损失。
基于Rotation的激活outliers抑制方法原理
SliceGPT首先提出了一种计算不变性(computational invariance),然后被QuaRot和QServe用于抑制激活outliers。相关论文:
SliceGPT: Compress Large Language Models by Deleting Rows and Columns
QuaRot: Outlier-Free 4-Bit Inference in Rotated LLMs
QServe: W4A8KV4 Quantization and System Co-design for Efficient LLM Serving
QuIP: 2-Bit Quantization of Large Language Models With Guarantees
QuIP#: Even Better LLM Quantization with Hadamard Incoherence and Lattice Codebooks

computational invariance
An invariant function is one for which a transformation to the input does not result in a change to the output.
SliceGPT提出了一种Q变换,也就是对LLM的矩阵乘的权重W(部分情况包括bias也要进行变换),一部分变为W*Q,一部分变为QT*W,但是transformer计算结果不变。
Q和其转置QT具有特殊性质:Let Q denote an orthogonal matrix
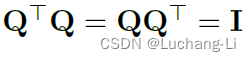
另外一个关键是RMSNorm具有一个特殊的性质,对输入x进行Q变换得到x*Q,那么输出y变为y*Q,保持了Q变换的传递。
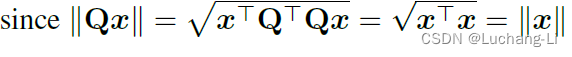
具体原理介绍
1, transformer网络的计算流程:
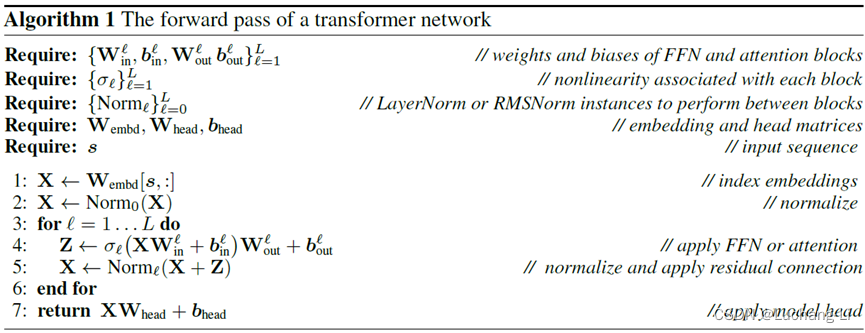
2, 施加Q变换流程:

3, 具体流程详解:
1. Embedding矩阵W乘以Q矩阵进行Q变换,使得经过embedding的激活由x变成x*Q。
进入transformer block后首先经过rms_norm,这个方法对结果保持了Q变换,也就是原来的输入x输出y,现在是输入x*Q输出y*Q。
2. 在进入attention之前,对Q,K,V的三个矩阵乘的参数变为QT*W,这样Q,K,V矩阵乘的输出原来是X*W,现在是(X*Q)*(QT*W) = X*(Q*QT)*W = X*W,也就是抵消了Q变换,不影响后续attention的计算。因为这个矩阵乘输出抵消了Q变换,所以bias保持不变。
3. attention输出后经过o_proj矩阵乘,o_proj的权重由W乘以Q矩阵进行Q变换,使得的激活由x1变成x1*Q。注意o_proj如果具有bias,也需要对bias变为bias*Q,才能正常对o_proj的输入进行完整的Q变换。
4. o_proj后是残差连接x+x1,因为残差另一个输入不像Q,K,V那样对Q进行了抵消,所以残差相加的激活x0和x1都经过Q变换,残差输出保持Q变换。
5. 然后到了FFN,首先是up_proj和gate_proj,这两个权重由W变为QT*W,跟上面Q,K,V矩阵乘一样,激活与变换后的权重相乘后抵消了Q变换。
6. 然后FFN的up_proj和gate_proj的结果经过激活函数到down_proj,down_proj的权重由W乘以Q,使得其输出进行Q变换。Bias跟o_proj一样需要进行变换。
7. FFN结果经过残差连接后进入下一个transformer block,循环进行上述2-6过程。
8. 最终lm_head的输入为x*Q,因此对lm_head的W变为QT*W,使得lm_head结果保持不变。
变换矩阵Q如何选择
理论上任何正交矩阵Q(满足Q*QT=I)都可以使用。
如果对整个模型所有transformer层应用一个统一的Q变换矩阵,那么,这两个变换可以完全融入矩阵乘的参数,跟AWQ一样,不引入任何额外的模型结构变化和计算量。
SliceGPT的方法
SliceGPT的目的主要是为了权重的剪枝,而不是激活outlier的抑制。因此其针对剪枝的需要并结合激活校准数据为每一层选择了特定的Q矩阵。
SliceGPT对每一层应用不同的Q变换矩阵,虽然可以通过Q和QT抵消一部分变换导致不引入额外的计算,但是残差连接处的两个输入激活具有不同的变换,这时就需要对其中一个输入变换到跟另一个输入一样的变换,两个结果才能相加。因此SliceGPT需要对残差的长程连接插入额外的矩阵乘计算:
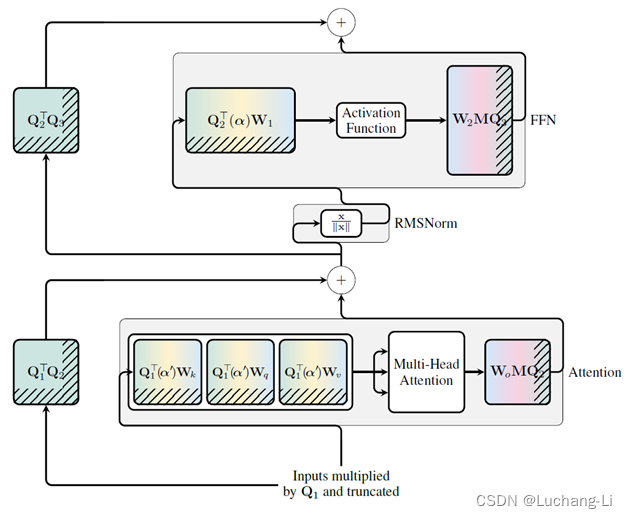
QuaRot的方法

we apply randomized Hadamard transformations to the weight matrices without changing the model. 特别之处在于采用了一个随机化的Hadamard矩阵。
We also apply online Hadamard transformations to the attention module to remove outlier features in keys and values, enabling the KV cache to be quantized.
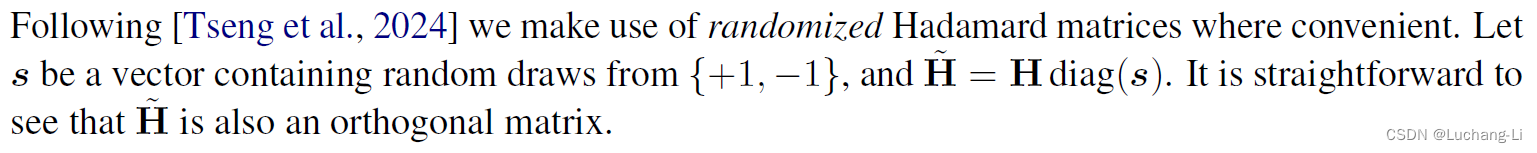
![]()

如果采用非随机化的Hadamard矩阵,或者所有曾使用一个固定的随机性的Hadamard矩阵,所有transformer层共用一个变换矩阵,不需要插入额外的矩阵乘从而引入任何额外计算量和模型结构变化。
上面原理部分中可以看出,有些矩阵乘的激活输入是没有得到处理的,包括q,k,v输出到o_proj的输入,ffn的up_proj和gate_proj输出到down_proj。QuaRot进行了进一步处理。
首先v_proj到o_proj可以针对每个head对应部分进行Hadamard变换,不需要插入额外的矩阵乘,对于v_proj和o_proj的hadamard矩阵获得方法如下:
had_mat = random_hadamard_matrix(head_size).numpy()
had_mat1 = np.kron(np.eye(head_num), had_mat)
而对于query和K cache的处理利用query和key的矩阵乘,分别query和key前面插入一个矩阵乘大小为head_size的变换矩阵乘对每个head对应部分进行变换,这样q k的矩阵乘结果对变换进行抵消,这个矩阵乘大小是比较小的,因此不会引入很大的overhead,如下图所示,Q变换矩阵乘大小只有head_size=128。也不会影响flash attention/flash decoding计算。
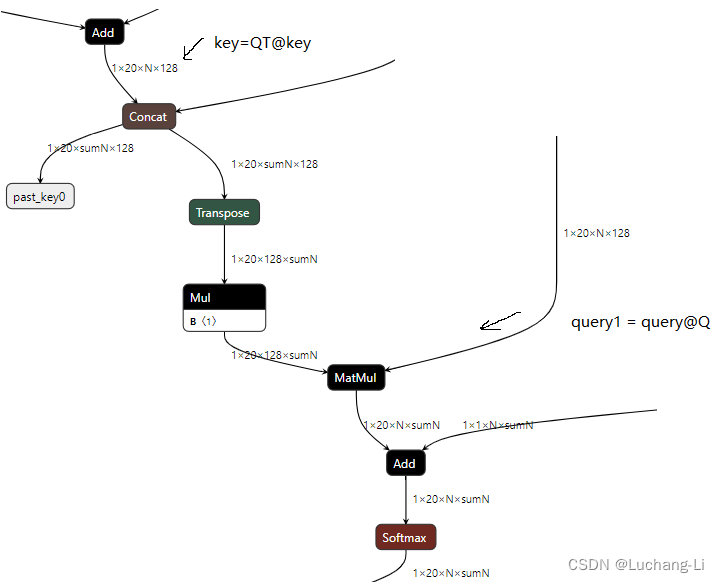
QServe对up_proj和down proj采用类似smoothquant的方法,根据激活得到一个scale向量来进行处理。采用了SmoothAttention对K cache的outlier迁移到query,而value不做处理,因为value cache不存在outliers.
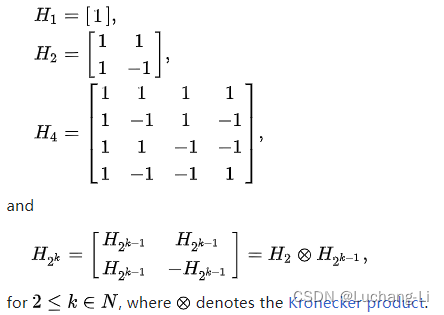
Hadamard matrix介绍
https://en.wikipedia.org/wiki/Hadamard_matrix
https://mathworld.wolfram.com/HadamardMatrix.html
据猜测,对于所有能被 4 整除的数,Hn都存在。
![]()

QServe的选择
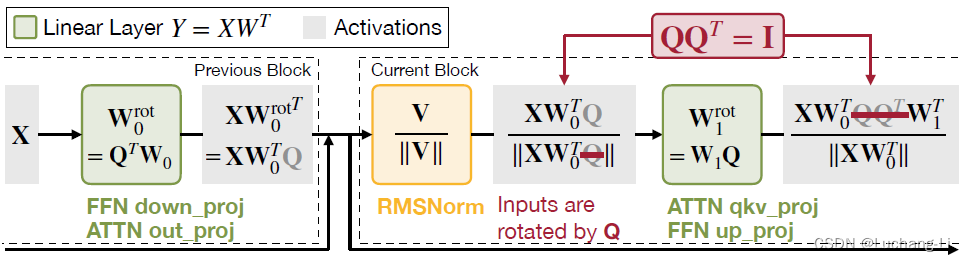
跟QuaRot类似但没有采用随机化的Hadamard矩阵:We simply choose the scaled Hadamard matrix as the rotation matrix. since rotation is a unitary transformation, the rotation matrix Q can be absorbed by the weights of the output module in the previous block.
看上去对整个模型采用统一的Q变换矩阵(scaled Hadamard matrix)因此无需改变模型结构和引入任何额外计算量。
因为QServe并没有像QuaRot那样采用激进的4bit激活量化,而是8bit激活量化,可能这样就足够而无需采用更复杂的方法,或者说虽然这样次优但是不会引入任何模型结构变化从而有利于部署。当然整个模型采用一个固定的scaled Hadamard或者随机的Hadamard矩阵哪个更好需要进一步评测。
实践
如何得到变换的Q矩阵
QuaRot开源的代码库中fake_quant/hadamard_utils.py或者quarot/functional/hadamard.py中定义了random_hadamard_matrix可以获取随机化和scale后的hadamard矩阵,使得其行列式为1或者-1,满足正交性:
https://github.com/spcl/QuaRot
import numpy as np
from hadamard_utils import random_hadamard_matrixN = 4096had_mat = random_hadamard_matrix(N, 'cpu')
had_mat_np = had_mat.numpy()# result is I
mat_result = np.matmul(had_mat_np, np.transpose(had_mat_np))
# result is 1 or -1
det = np.linalg.det(had_mat_np)
RMSNorm/LayerNorm处理
LayerNorm不满足Q变换的传递性,需要转换为LayerNorm,QuaRot提出了一种把LayerNorm转换为RMSNorm的方法。另外只有标准的RMSNorm即x/||x||才满足Q变换传递性,但是实际llama2, baichuan, qwen等模型用的RMSNorm还具有一个scale向量。需要融合到后面矩阵乘的参数里面才能实现计算等价。
有QuaRot还需不需要GPTQ/AWQ?
有待评测
总的来说,如果只是想简单的抑制激活的outliers从而提升激活量化精度,当然对权重量化应该也大有益处,QServe的方法应该是个不错的尝试起点。
本人使用Qwen1.5 5b chat验证,通过打印出矩阵乘激活通道间的绝对平均值,发现确实能够显著抑制激活的outlier:
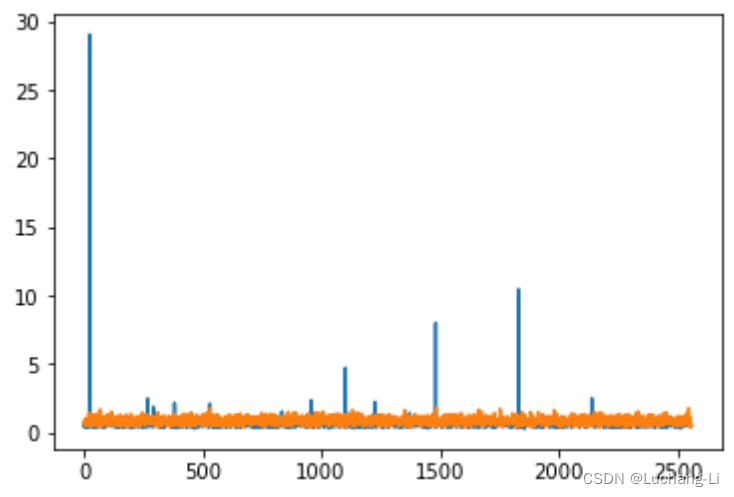
但作者实践结果是,部分模型仅靠原理的部分用Hadamard matrix进行处理后,激活不量化而4bit权重量化却发现精度显著下降⊙︿⊙。很可能是这个方法有利于激活但是放大了权重量化损失。