New Work-flow of Circuit Bootstrapping

参考文献：

[CGGI17] Chillotti I, Gama N, Georgieva M, et al. Faster packed homomorphic operations and efficient circuit bootstrapping for TFHE. ASIACRYPT 2017 (1): 377-408.
[CDKS21] Chen H, Dai W, Kim M, et al. Efficient homomorphic conversion between (ring) LWE ciphertexts. ACNS 2021 (1): 460-479.
[KLD+23] Kim A, Lee Y, Deryabin M, et al. LFHE: Fully homomorphic encryption with bootstrapping key size less than a megabyte[J]. Cryptology ePrint Archive, 2023.
[DKMS24] De Micheli G, Kim D, Micciancio D, et al. Faster amortized FHEW bootstrapping using ring automorphisms. Public Key Cryptography 2024 (4): 322-353.
[WWL+24] Wang R, Wen Y, Li Z, et al. Circuit Bootstrapping: Faster and Smaller. EUROCRYPT 2024 (2): 342-372.
Leveled mode of TFHE
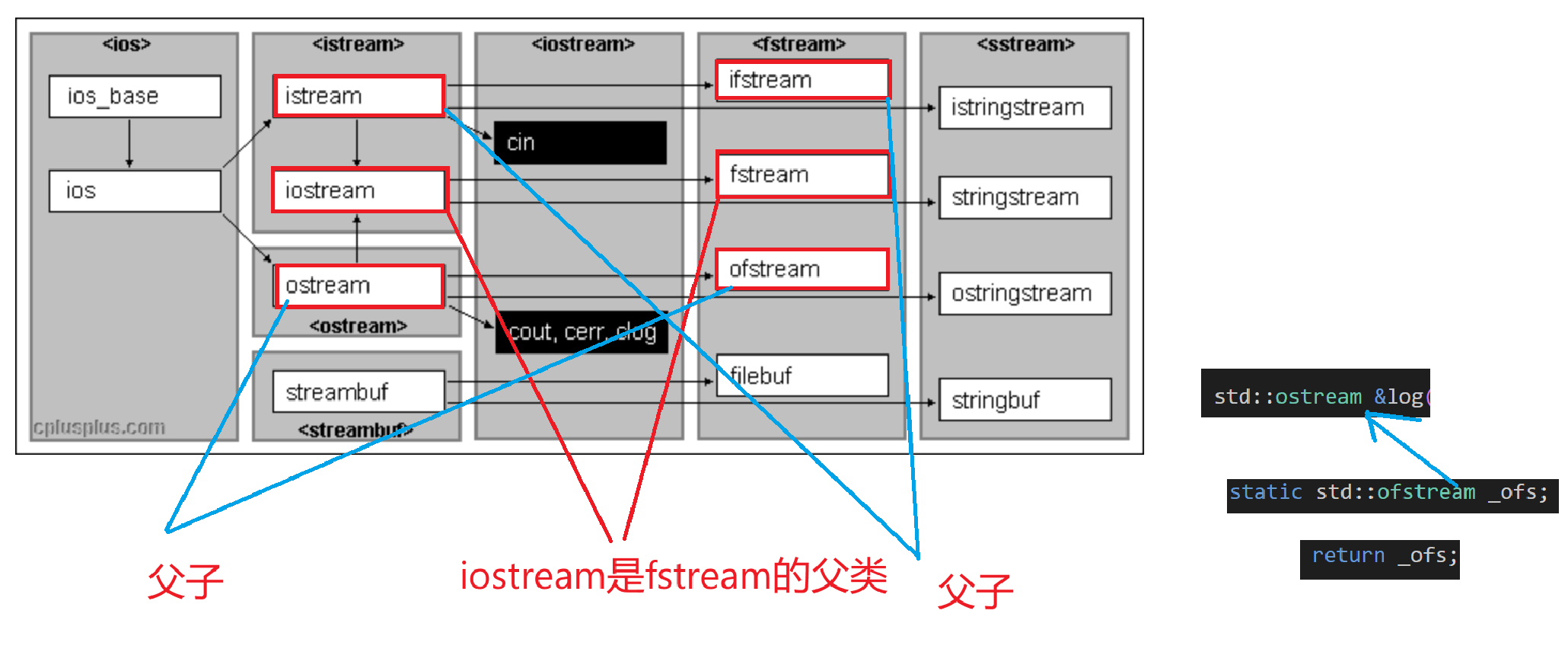
Conversion Between ®LWE
加权自动机：在 Semirings 上建模

文章目录

LHE Mode
- Original TFHE
- Novel Work Flow
Automorphism-Based PBS
- Using Sparse Isomorphism
- MV-PBS
Analysis & Parameters

LHE Mode

TFHE 除了有 FHE mode，还有 [CGGI17] 提出的 LHE mode：

前者每个 Gate 都需要自举，利用 LinPoly + PBS 实现布尔运算；
后者仅在噪声过大或者类型不符时才自举，利用 det-WFA + CMux-based OBDD + BRS 实现布尔运算。由于 RLWE 和 RGSW 外积的噪声增长不对称性，只要 RGSW 加密消息的范数很小（比如：布尔值、单项式），那么 LHE 的容许 CMux 深度就会很大。

自动机的运算：

在这里插入图片描述

决策树的运算：

在这里插入图片描述

比特序列表示的运算：

在这里插入图片描述

但是，它们都是用 CMux Gate 搭建的，控制位是 RGSW 密文（布尔值/单项式的 Powers-of-Base），数据位是 RLWE/LWE 密文（系数编码）。如果想要把数据位提升到控制位，就需要 LWE-to-RGSW 的密文转换，也就是 “电路自举”。

Original TFHE

[CGGI17] 的电路自举的工作流如下：

在这里插入图片描述

他们使用三组参数：

$(\underline{q}, \underline{n})$ 是 Level 0 的 LWE 参数集，存储数据，具有最高的噪声。模数和维度都尽可能小，使得自举更高效。
$(q, N)$ 是 Level 1 的 RGSW 参数集，存储控制位。模数和维度的规模，决定了外积的效率和深度。
$(\overline{Q}, \overline{N})$ 是 Level 2 的 RLWE 参数集，用于 PBS 自举，具有最小的噪声。选取足够大的模数，获得所需的深度。

电路自举包含两个步骤：令 $v=(v_0,v_1,\cdots,v_{l-1})$ 是 RGSW 使用的 Gadget Vector，令 $\underline{sk},sk,\overline{sk}$ 分别是三层的私钥。

Functional Bootstrapping Step，
- 输入单个 Level-0 LWE 密文 $LWE_{\underline{sk}}(m)$ ，使用 $l$ 次 PBS 计算出 $LWE_{\overline{sk}}(mv_i)$ ，
- 这里可以使用 [CLOT21] 的 PBSmanyLUT 加速。
Ciphertext Conversion Step，
- RGSW 密文的第一部分：使用 LWE-to-RLWE PubKS 过程，把 $(b,a)=LWE_{\overline{sk}}(mv_i)$ 切换到 $RLWE_{sk}(mv_i)$
  
  使用的 KSK 是 $RLWE'_{sk}(\overline{sk_j})$ ，计算过程是
  $\sum_j a_j \odot RLWE'_{sk}(\overline{sk_j})$
- RGSW 密文的第二部分：使用 LWE-to-RLWE PriKS 过程，把 $LWE_{\overline{sk}}(mv_i)$ 切换到 $RLWE_{sk}(sk \cdot mv_i)$
  
  使用的 KSK 是 $RLWE'_{sk}(sk \cdot \overline{sk_j})$ 以及 $RLWE'_{sk}(sk)$ ，计算过程是
  $\odot RLWE'_{sk}(sk) + \sum_j a_j \odot RLWE'_{sk}(sk \cdot \overline{sk_j})$
- 最后把 $RLWE_{sk}(mv_i)$ 和 $RLWE_{sk}(sk \cdot mv_i)$ 组装成 $RGSW_{sk}(m)$ 密文即可。上述的 PubKS 和 PriKS 也可以采用 pre-computed variant，提高效率、降低噪声，代价是更大的 KSK 规模。

对于计算开销：使用 MV-PBS 之后，实际上 Ciphertext Conversion Step 占据了大部分。对于存储开销：也是 Ciphertext Conversion Step 中的 KSK 占据了大部分。

疑问：为何不使用 [CDKS21] 的基于自同构的 LWE-to-RLWE 呢？

[CGGI17] 的 PubKS 或 PriKS，需要 $\overline{N}$ 次和标量 $a_j \in \mathbb Z_{\overline Q}$ （系数表示下分解和数乘）的外积运算，每次都需要 $2 lN$ 次模乘，共计 $2l\overline NN$
基于自同构的 LWE-to-RLWE，需要 $\overline{N}/N \cdot\log n$ 次和多项式 $\in R_{\overline Q,n}$ （系数表示下分解，再转化为 NTT 表示）的外积运算（长度 $\overline{N}$ 的内积表示为 $\overline{N}/N$ 个长度 $N$ 的卷积），每次都需要 $2(l+1)N\log N + 2lN$ 次模乘，共计 $2(l+1)\overline{N}\log^2 N + 2l\overline{N}\log N$
假如 $N = 1024$ ，那么 $\log^2 N = 100 \ll N$ ，效率提升应当十分显著，密钥规模也小得多，噪声方差会偏大 $\overline{N}\log N$ 因子。

Novel Work Flow

[WWL+24] 提出了新的工作流，移除了 ACC to LWE 步骤，直接把 ACC 重构为 RGSW（实际上就是把 Extract 和基于自同构的 LWE-to-RLWE 合并了），从而消除了开销最大的 PubKS 和 PriKS 过程。

在这里插入图片描述

仅使用 Level 0 和 Level 2 两组参数集，新的电路自举流程是：

PBS Without Sample Extraction，
- 输入单个 Level-0 LWE 密文 $LWE_{\underline{sk}}(m)$ ，使用 $l$ 次 PBS 计算出
  $RLWE_{\overline{sk}}(\overline{N}^{-1}mv_i+\sum_{k=1}^{\overline{N}-1}y_k X^k)$
  预期的明文在常数项（缩放 $\overline{N}^{-1}$ 抵消后续自同构的影响），其余的系数是冗余的。
- 这里使用了 [WWL+24] 优化的 Automorphism-Based MV-PBS 算法。
Ciphertext Conversion，

RGSW 密文的第一部分：使用 [CDKS21] 提出的 Trace 稀疏分解算法（分圆塔），使用 Galois自同构 $\tau_{2^k+1}, k=\log \overline{N},\cdots,2,1$ 对应的 KSK，计算出 $RLWE_{\overline{sk}}(mv_i)$
RGSW 密文的第二部分：使用 [DKMS24] 提出的 RLWE’-to-RGSW 技术，给定 $RLWE'_{\overline{sk}}(\overline{sk}^2)$ ，计算
$\odot RLWE'_{\overline{sk}}(\overline{sk}^2) = RLWE_{\overline{sk}}(\overline{sk} \cdot mv_i + \overline{sk} \cdot e)$
其中 $\in R_{\overline{Q},\overline{N}}$ 是 $RLWE_{\overline{sk}}(mv_i)$ 的噪声。
最后把 $RLWE_{\overline{sk}}(mv_i)$ 和 $RLWE_{\overline{sk}}(\overline{sk} \cdot mv_i)$ 组装成 $RGSW_{\overline{sk}}(m)$ 密文即可。

Ciphertext Conversion 的算法是：

在这里插入图片描述

总体的复杂度是：

在这里插入图片描述

疑问：文章说由于 step 2 无法切换维度，因此就把 RGSW 留在 Level 2 参数集。但是，这会导数 LHE 的计算开销较大（自举噪声和密钥切换噪声都累积在 $KaTeX parse error: Got function '\overline' with no arguments as subscript at position 11: \mathbb Z_\̲o̲v̲e̲r̲l̲i̲n̲e̲{Q}$ 的低位，没必要保留）。可以依然使用中等规模的参数 $(q, N)$ ，可修改为：

使用 Ring-Swich 技术，额外要求 $\overline{sk} \in R_{N} \le R_{\overline{N}}$ ，首先把 ACC 模切换到安全的模数 $q$ ，然后直接提取出维度 $N$ 子环（含有所需的常数项），这几乎是免费的
现在 ACC 是参数 $(q, N)$ 下的 RLWE 密文，执行 Trace 消除冗余系数，然后做成 RGSW 密文，执行 LHE 运算
这样做，step 1 完全不变（稀疏私钥的安全性），step 2 速度更快、存储更小

如果不想要稀疏私钥，也可以这么做：依旧提取出维度 $\overline{N}$ 的 LWE 密文，然后分成 $\overline{N}/N$ 个区间（内积 = 卷积），使用 [CDKS21] 的基于自同构的 LWE-to-RLWE 算法，仅需 $\overline{N}/N$ 次调用，效率损失也很小。

Automorphism-Based PBS

[WWL+24] 使用了两种 PBS Without Sample Extraction 算法，其一是 CMux-based Blind Rotation，其二是 Automorphism-Based Blind Rotation。

[WWL+24] 对前者的 Level 0 使用二元秘密（ $\|s\|_2^2 = \underline{n}/2$ ），对后者的 Level 0 使用 $\sigma=3.2$ 的高斯秘密（ $\|s\|_2^2 = \underline{n}\sigma^2$ ）。为了降低模切换噪声（大约是 $\sigma_{ms}^2 = (\|s\|_2^2+1)/12$ ），[WWL+24] 两者的 Level 2 都使用二元秘密。

Using Sparse Isomorphism

[LMK+23] 的基于自同构的自举，关键是使用了同构 $\mathbb Z_{2N}^* \cong \mathbb Z_{N/2} \times \mathbb Z_2$ ，生成元是 ${g,-1\}$ 。要求系数形如 $\in \mathbb Z_{2N}$ ，从而可以表示为 $±gj \pm g^{j}$ 形式，只需要准备 $2$ 个 KSK，使用 Galois 自同构计算指数上的数乘 $X^{a_i \cdot s_i} = \tau_{\pm g^j}(X^{s_i})$

为了进一步提高自举效率（和 $a_i$ 不同取值的数量有关），[WWL+24] 使用了更加稀疏的系数，形如 $\cdot 2^\nu +1 \in \mathbb Z_{2N}$ ，只要 $\ge 8$ 并且 $\nu \ge 2$ ，则它们构成了某个元素 $\in \mathbb Z_{2N}$ 生成的乘法循环群，只需要准备 $1$ 个 KSK 即可。易知 $\bmod 2N)=N/2$ ，因此可以选取 $g=5^{2^{\nu-2}}$

类似于 [LMK+23]，只要系数 $a_i$ 都具有 $\cdot 2^\nu+1$ 形式，那么就可以把内积写成关于 $g$ 的多项式，再使用 Horner 法则整理为：
$\sum_i a_i s_i = P_s(g) := \sum_{j \in I_0} s_j + g\left(\cdots+g\left(\sum_{j \in I_{2N/2^\nu}-1}s_j\right)\right) \pmod{2N}$
其中 $I_j = \{i: a_i = g^j\}, j=0,1,\cdots,2N/2^\nu-1$

由于 $2N/2^\nu$ ，盲旋转总共执行了 $2N/2^\nu-1$ 次串行的 $\tau_g$ 自同构，因此初始 ACC 加密 $T V (X)$ ，则最终计算出 $TV(X^{g^{-1}}) \cdot X^{\sum_i a_i s_i}$ ，因此需要预先把 test vector 扭曲 $\to X^g$ ，保证计算结果的正确性。

在执行盲旋转之前，使用 $\lfloor x \rceil_{k \cdot 2^\nu+1}$ 把 LWE 系数都舍入到合适的形式，这里的舍入噪声会比 [LMK+23] 更大。

在这里插入图片描述

也采用了 [LMK+23] 的窗口技术，进一步降低自同构的数量。

在这里插入图片描述

由于期望值难以计算，为了确定最优的窗口大小，他们使用 Monte Carlo simulation 统计出不同 $w$ 对应的自同构数量。对于不同维度 $2N/2^\nu$ ，试验出的最佳 $w$ 是：

在这里插入图片描述

完整的 PBS 算法是：

在这里插入图片描述

MV-PBS

由于 LWE 密文舍入到的 $(b, a)$ 都是 $\cdot 2^\nu+1$ 形式的整数，而非 $2^\nu$ 倍数，因此无法直接成为 Multi-Value PBS。可以采取很简单的技巧：
$X^{b+\sum_i a_is_i} = X^{b+\sum_i(a_i+1)s_i - \sum_i s_i}$
其中的 $(b, a)$ 都是 $2^\nu$ 的倍数，从而 $b+\sum_i a_is_i$ 也都是 $2^\nu$ 的倍数。这额外需要 $RGSW_{\overline{sk}}(X^{- \sum_i \underline{sk}_i})$ 作为辅助信息。

用于电路自举的 MV-PBS 算法如下：计算符号函数、不做密文提取。

在这里插入图片描述

完整的 PBS 算法是：

在这里插入图片描述

Analysis & Parameters

为了减少 Gadget Vector 的长度，[WWL+24] 对于所有的外积都使用了 [KLD+23] 的 Approximate Gadget Decomposition，选取 $B^l < q$ ，那么 $(\delta,\delta B,\cdots,\delta B^{l-1})$ ，其中 $\delta = \lceil q/B^l \rceil$ ，近似误差 $\epsilon \le \delta/2$ ，环元素和 $R L W E^{'} (m)$ 的外积噪声是 $\sigma^2 \le lNB^2\sigma_{fresh}^2/12 + Var(m)\cdot\epsilon^2/3$ （减少了前者，增加了后者，做个平衡），其中 $\le \|m\|_2^2$ 。如果是 $R L W E$ 和 $RGS W$ 的外积，则还有 $\|m\|_2^2 \cdot \sigma_{RLWE}^2$ 的影响。

有五个不同的 Gadget Vector，它们的 $R L W E^{'}$ 的消息格式为

执行 LHE mode 运算：维度 $\overline{N}$ ，模数 $\overline{Q}$ ，控制位形如 $m=bX^i, b \in \{0,1\}$ ，因此 $\|m\|_2^2 \le 1$
PBS 中的外积：维度 $\overline{N}$ ，模数 $\overline{Q}$ ，CMux-based 形如 $m=\underline{sk}_i$ （二元），Auto-based 形如 $m=X^{\underline{sk}_i}$ （高斯），都是 $\|m\|_2^2 \le 1$
PBS 中的自同构：维度 $\overline{N}$ ，模数 $\overline{Q}$ ，CMux-based 中不存在，Auto-based 形如 $m=\overline{sk}(X^{g^j})$ ，满足 $\|m\|_2^2 \le \overline{N}/2$
密文转换中的迹映射：维度 $\overline{N}$ ，模数 $\overline{Q}$ ，形如 $m=\overline{sk}(X^{g^u})$ ，满足 $\|m\|_2^2 \le \overline{N}/2$
密文转换中的乘以私钥：维度 $\overline{N}$ ，模数 $\overline{Q}$ ，形如 $m=\overline{sk}^2$ （二元），满足 $\|m\|_2^2 \le \overline{N}^2/4$