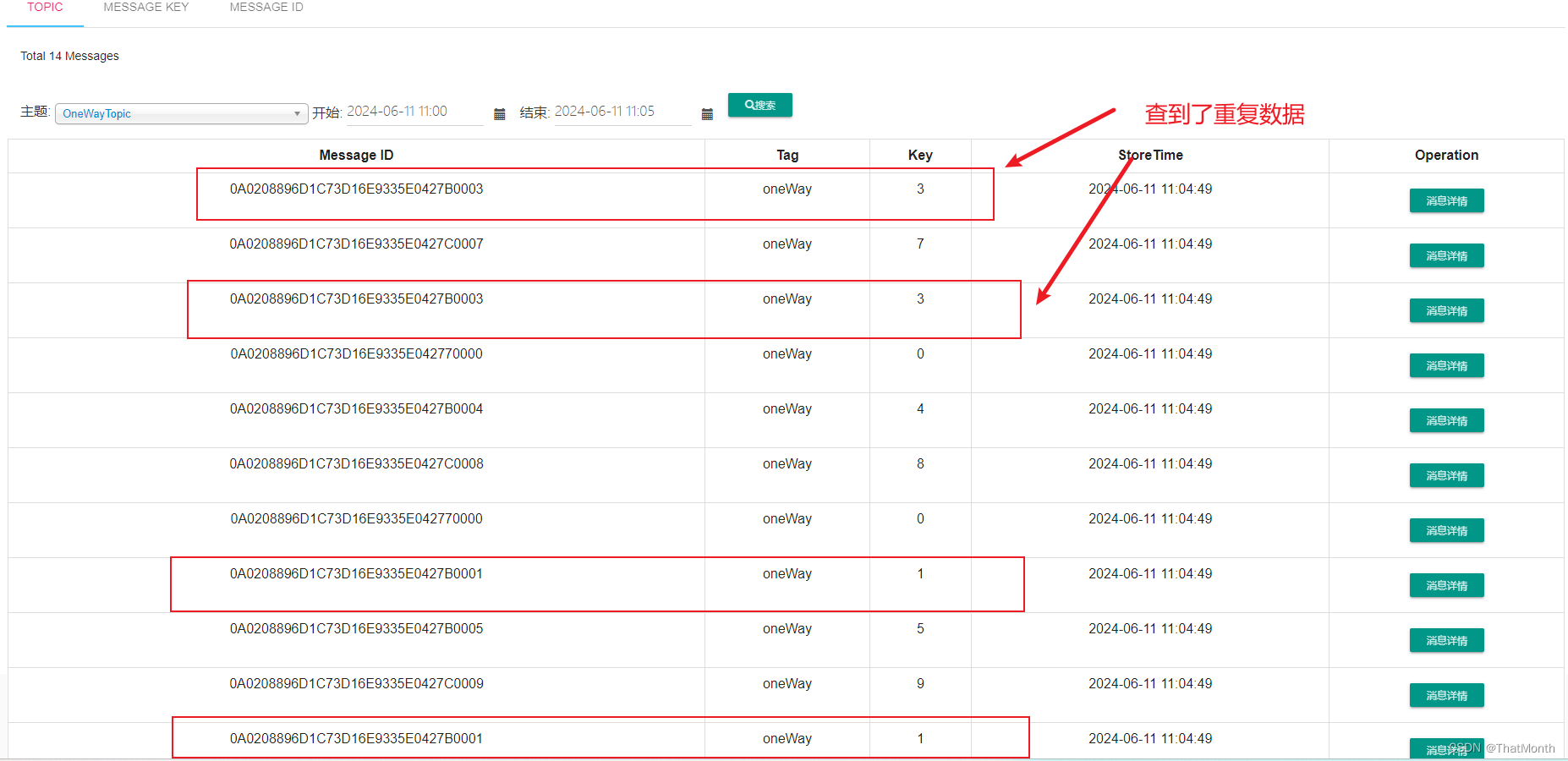
目录
前言:
1 链式二叉树的创建
2 前序 中序 后序遍历
3 树的节点个数
4 树的高度
5 树的叶子节点个数
6 树的第K层节点个数
前言:
链式二叉树我们在C语言阶段已经实现了,这里介绍的是涉及到的部分问题,比如求树的高度,求树的节点个数等,连接部分就手动连接,用一个样例来介绍涉及到的几个问题。
这里对前面知识反馈比较大的是递归,可以说每个问题都用到了递归。
1 链式二叉树的创建
因为是链式二叉树,所以有两个指针,分别指向右孩子节点和左孩子节点,给上值,手动连接即可:
typedef struct TreeNode
{struct TreeNode* left = NULL;struct TreeNode* right = NULL;int data;
}TreeNode;TreeNode* Tree()
{TreeNode* node1 = new TreeNode;TreeNode* node2 = new TreeNode;TreeNode* node3 = new TreeNode;TreeNode* node4 = new TreeNode;TreeNode* node5 = new TreeNode;TreeNode* node6 = new TreeNode;//TreeNode* node7 = new TreeNode;node1->data = 1;node2->data = 2;node3->data = 3;node4->data = 4;node5->data = 5;node6->data = 6;//node7->data = 7;node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;//node5->left = node7;return node1;
}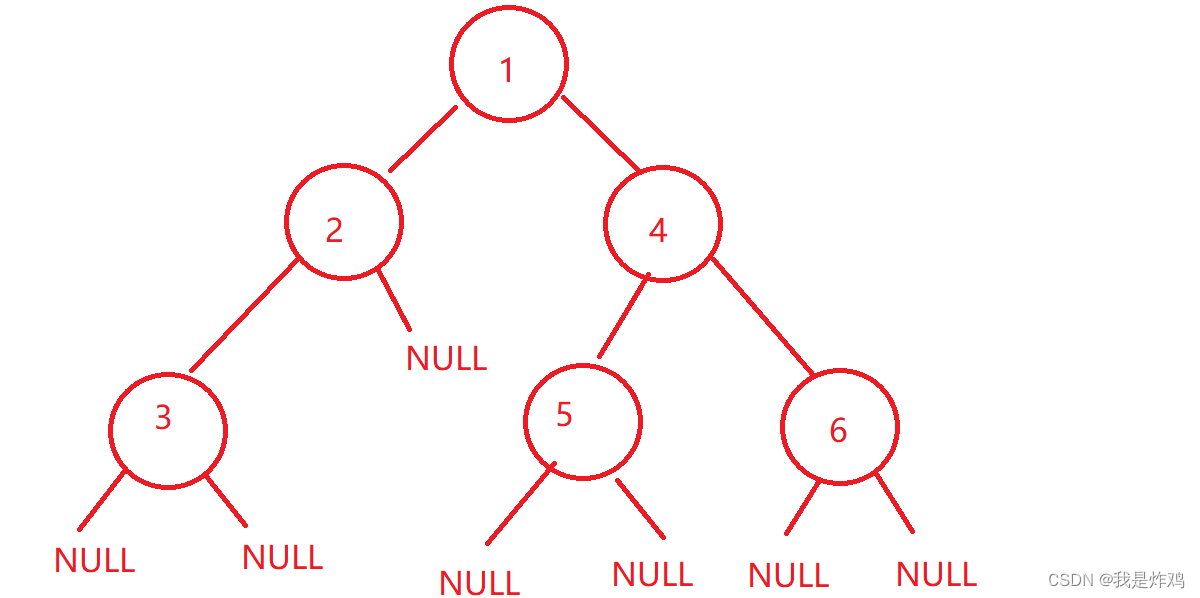
整体构建出来就是这样,对于初学链式二叉树的同学来说,NULL给上是很有必要的,这对于后面的遍历问题有帮助。
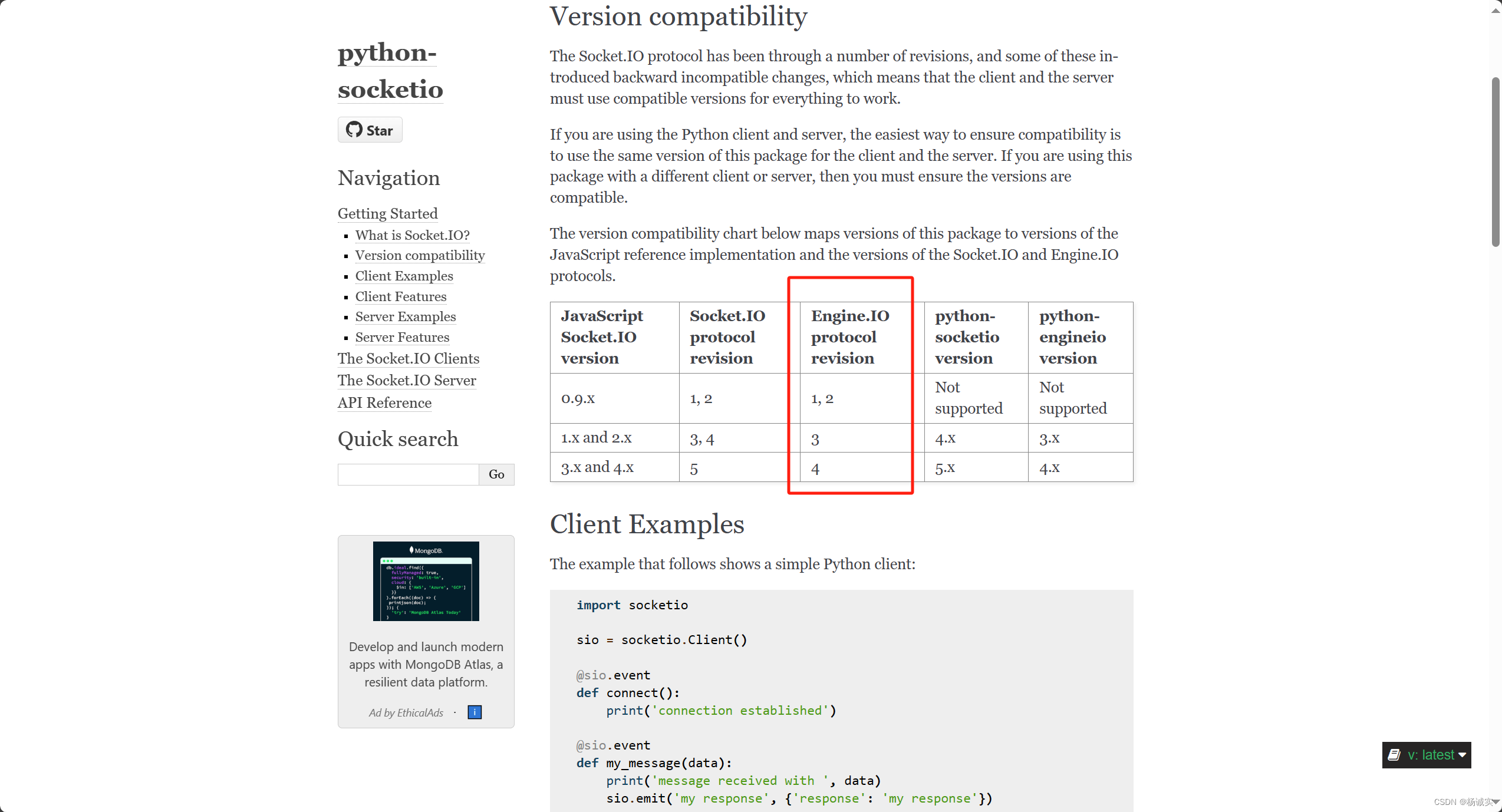
2 前序 中序 后序遍历
前序遍历的顺序是 根 左子树 右子树,中序遍历的的顺序是左子树 根 右子树 ,后序遍历的顺序是左子树,右子树,根。
咱们从前序开始,顺便进行打印,从1开始,到左子树是2,2的左子树是3,3是左子树是NULL,再往下就没了,递归回来是3的右子树,那么此时2的左子树就遍历完成了,2的右子树是NULL,这时候1的左子树就遍历完了,然后是右子树,到4,然后是4的左子树5,接着是5的左右子树,这时4的左子树就遍历完了,然后是右子树,当6遍历完了之后,才是整个树都遍历完了。
那么代码会不会很复杂呢?
不会,递归都有一个特点,思路难想,代码简单:
void PrevOrder(TreeNode* root)
{if (root == NULL){cout << "N ";return;}cout << root->data << " ";PrevOrder(root->left);PrevOrder(root->right);
}
这就遍历完了。
打印的结果是1 2 3 N N N 4 5 N N 6 N N,那么为了加强理解我们可以这样看:

3 N N N是2的左右子树,5 N N 6 N N是4的左右子树,2 4 是1 的左右子树,这样结合起来就好理解多了。
那么对于中序后序来说都是一样的,这里给代码,就不重复演示了:
void InOrder(TreeNode* root)
{if (root == NULL){cout << "N ";return;}InOrder(root->left);cout << root->data << " ";InOrder(root->right);
}void BackOrder(TreeNode* root)
{if (root == NULL){cout << "N ";return;}BackOrder(root->left);BackOrder(root->right);cout << root->data << " ";
}3 树的节点个数
树的节点个数问题,使用的是分而治之的思想,比如一个院,要统计有多少人,那么院长就发号司令,副院长去问班主任,班主任去问辅导员,辅导员去问班长,然后加上自己,最后就可以得到总总共的人数。
树的节点个数是一样的,求总节点个数,我们可以把树分为左右子树,把一个树拆分成无数的左右子树,统计每个左右子树的节点个数,相加即可。
代码实现:
size_t TreeSize(TreeNode* root)
{return root == NULL? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}是的,代码就这么简单,这里给上递归展示图看看:
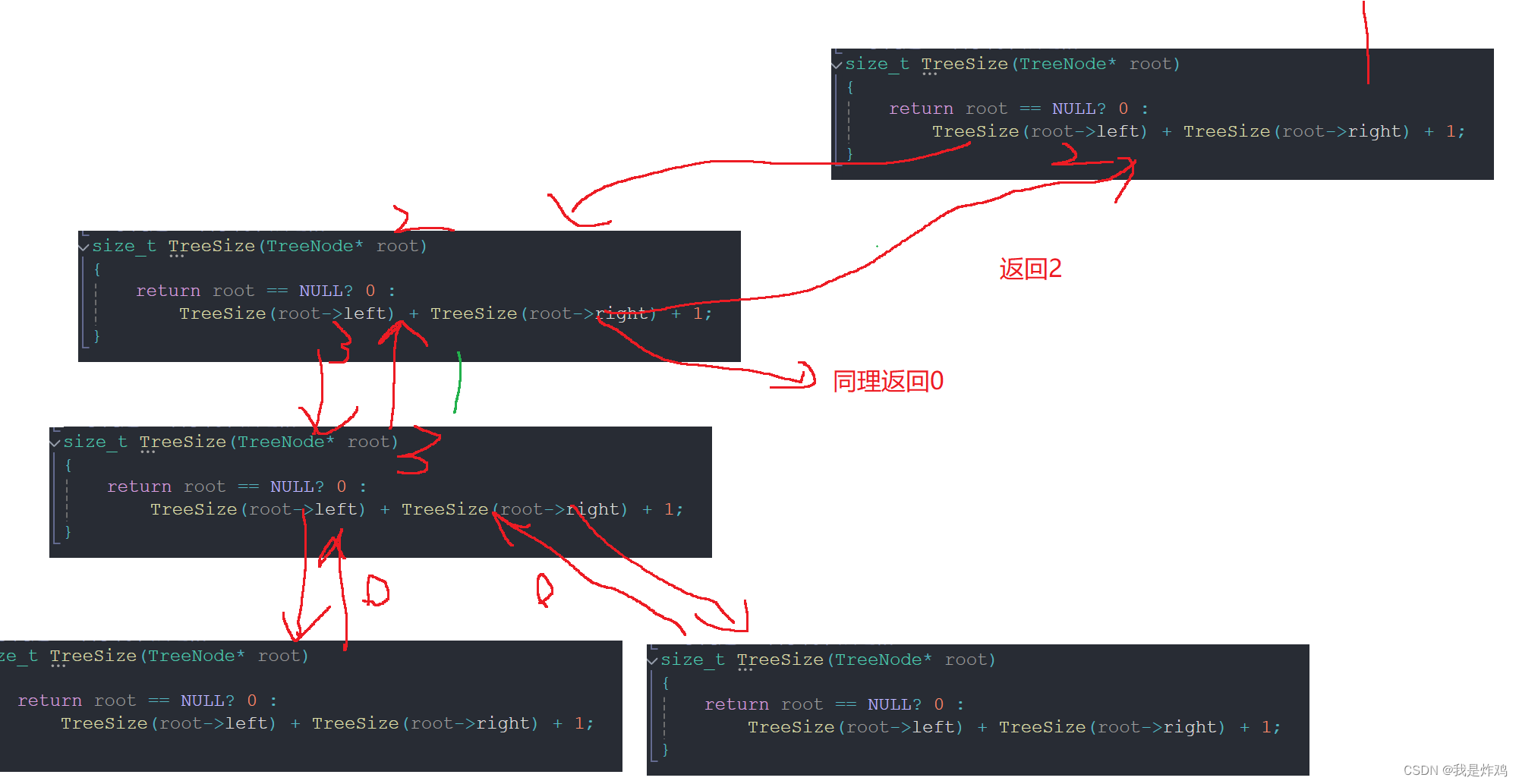
这里递归的是1的右子树。
4 树的高度
树的高度同理,我们可以理解为两个院的人比最高的,树的高度即我们同理,返回左右子树高度最高的即可,因为一个节点本身就算1,所以返回高度的时候需要加1,返回的条件就是节点为空,为空就返回0:
size_t TreeHeightError(TreeNode* root)
{return root == NULL ? 0 : TreeHeight(root->left) > TreeHeight(root->right) ?TreeHeight(root->left) + 1 : TreeHeight(root->right) + 1;
}以上代码看起来是没问题的,100个样例能跑过90的样例,但是数据量一多就会崩盘,因为这里没有记录左右子树的高度,也就是说会重复计算,这里不要小看重复计算,没有记录那么所有的计算都会翻二倍,而每一层都没有记录,所有越往层数多的走,就会变成2^n的重复计算,是指数量级的增长,所以我们应该记录数据:
size_t TreeHeight(TreeNode* root)
{if (root == NULL) {return 0;}size_t leftHeight = TreeHeight(root->left);size_t rightHeight = TreeHeight(root->right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}5 树的叶子节点个数
叶子节点即没有孩子节点的孩子,那么返回1的条件就是左右孩子都为空,如果不为空往下遍历就ok了:
size_t TreeLeaf(TreeNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}return TreeLeaf(root->left) + TreeLeaf(root->right);
}6 树的第K层节点个数
这是本文最难的一个问题了,该问题的子问题是:
空节点的时候返回0,k = 1的时候返回1,K > 1的时候遍历即可,个人认为k - 1是这个问题的关键所在:
size_t TreeNodeK(TreeNode* root,size_t k)
{if (root == NULL){return 0;}if (k == 1){return 1;}return TreeNodeK(root->left, k - 1) +TreeNodeK(root->right, k - 1);
}因为遍历是从根节点开始遍历的,所以减到k = 1的时候,是涉及到的那层,对该层进行判断,这是存在一个顺序问题,root == NULL应该在k == 1之前,因为递归到那一层,k = 1是铁定的,这时候就需要先判断是不是空节点,不是空节点再讨论K= 1的问题。
以上所有问题的测试代码:
int main()
{TreeNode* node = Tree();size_t k = 2;//前序遍历PrevOrder(node);cout << endl;//中序遍历InOrder(node);cout << endl;//后序遍历BackOrder(node);cout << endl;//树的节点个数cout << "The Tree's size is:" << TreeSize(node) << endl;//树的高度cout << "The Tree's Height is:" <<TreeHeightError(node) << endl;//树的叶子节点个数cout << "The Tree's leaf is:" <<TreeLeaf(node) << endl;//树的第K层节点个数cout << "The Tree's leaf about K is:" <<TreeNodeK(node,k) << endl;return 0;
}感谢阅读!