W5 Lists_stacks_queues_priority queues

    To explore the relationship between interfaces and classes in the Java Collections Framework hierarchy.
    To use the common methods defined in the Collectioninterface for operating collections.
    To use the Iteratorinterface to traverse the elements in a collection.
    To use a for-each loop to traverse the elements in a collection.
    To explore how and when to use ArrayListor LinkedListto store elements.
    To compare elements using the Comparableinterface and the Comparator interface.
    To use the static utility methods in the Collectionsclass for sorting, searching, shuffling lists, and finding the largest and smallest element in collections.
    To distinguish between Vectorand ArrayListand to use the Stackclass for creating stacks.
    To explore the relationships among Collection, Queue, LinkedList, and PriorityQueueand to create priority queues using the PriorityQueueclass.
    To use stacks to write a program to evaluate expressions.

Data sturcture

A data structure or collection is a collection of data organized in some fashion
not only stores data but also supports operations for accessing and manipulating the data
In object-oriented thinking, a data structure, also known as a container, is an object that stores other objects, referred to as elements

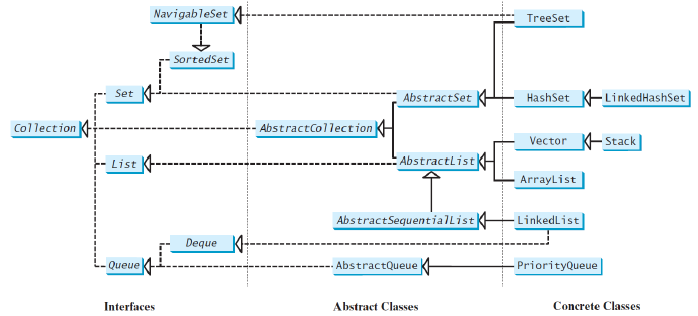
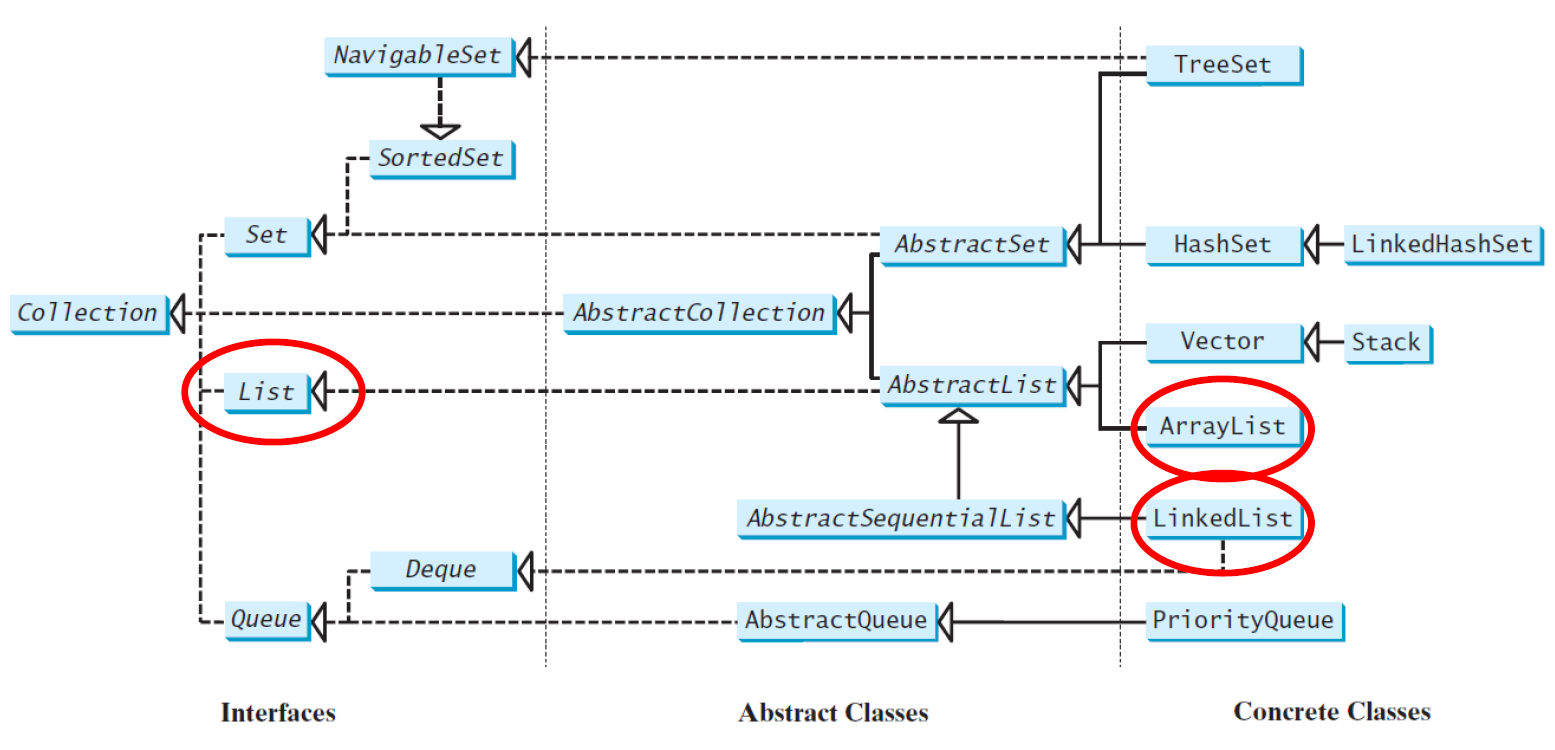
Java Collections Framework hierarchy

Java Collections Framework支持两种类型的容器:

1) One for storing a collection of elements, simply called a collection

    Lists store an ordered collection of elements
    Sets store a group of nonduplicate elements
    Stacks store objects that are processed in a last-in, first-out fashion
    Queues store objects that are processed in a first-in, first-out fashion
    PriorityQueues store objects that are processed in the order of their priorities

2) One for storing key/value pairs, called a map
p.s: 这玩意就是python里的字典

    The Collection interface is the root interface for manipulating a collection of objects
abstract collection类提供了collection接口的部分实现(collection中的所有方法，除了add、size和iterator方法)

注意：The Collection interface应用了 Iterable接口

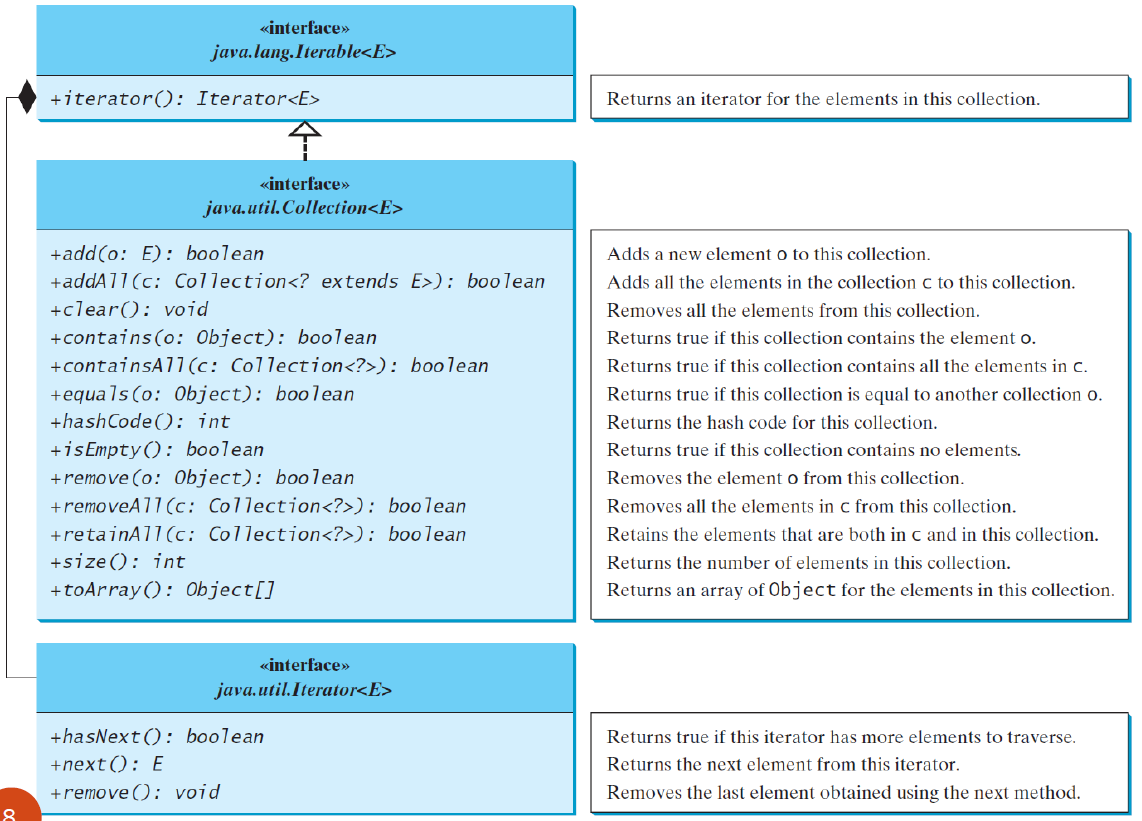
    All the concrete classes in the Java Collections Framework implement the java.lang.Cloneable and java.io.Serializable interfaces except that java.util.PriorityQueue does not implement the Cloneable interface
    Collection interface中的一些方法不能在具体的子类中实现(例如，只读集合不能添加或删除)否则java.lang.UnsupportedOperationException

Iterator

Each collection is Iterable

List

有序，有索引，可重复

    A list collection stores elements in a sequential order, and allows the user to specify where the element is stored
    The user can also access the elements by index
    The Listinterface stores elements in sequence and permits duplicates
    Two concrete classes in Java Collections Framework: ArrayListand LinkedList

Iterator

listtiterator()和listtiterator (startIndex)方法返回一个listtiterator的实例
listtiteratorinterface扩展了Iteratorinterface，用于双向遍历列表并向列表中添加元素

    The nextIndex()method returns the index of the next element in the iterator, and the previousIndex()returns the index of the previous element in the iterator
    The add(element)method inserts the specified element into the list immediately before the next element that would be returned by the next()method defined in the Iterator interface

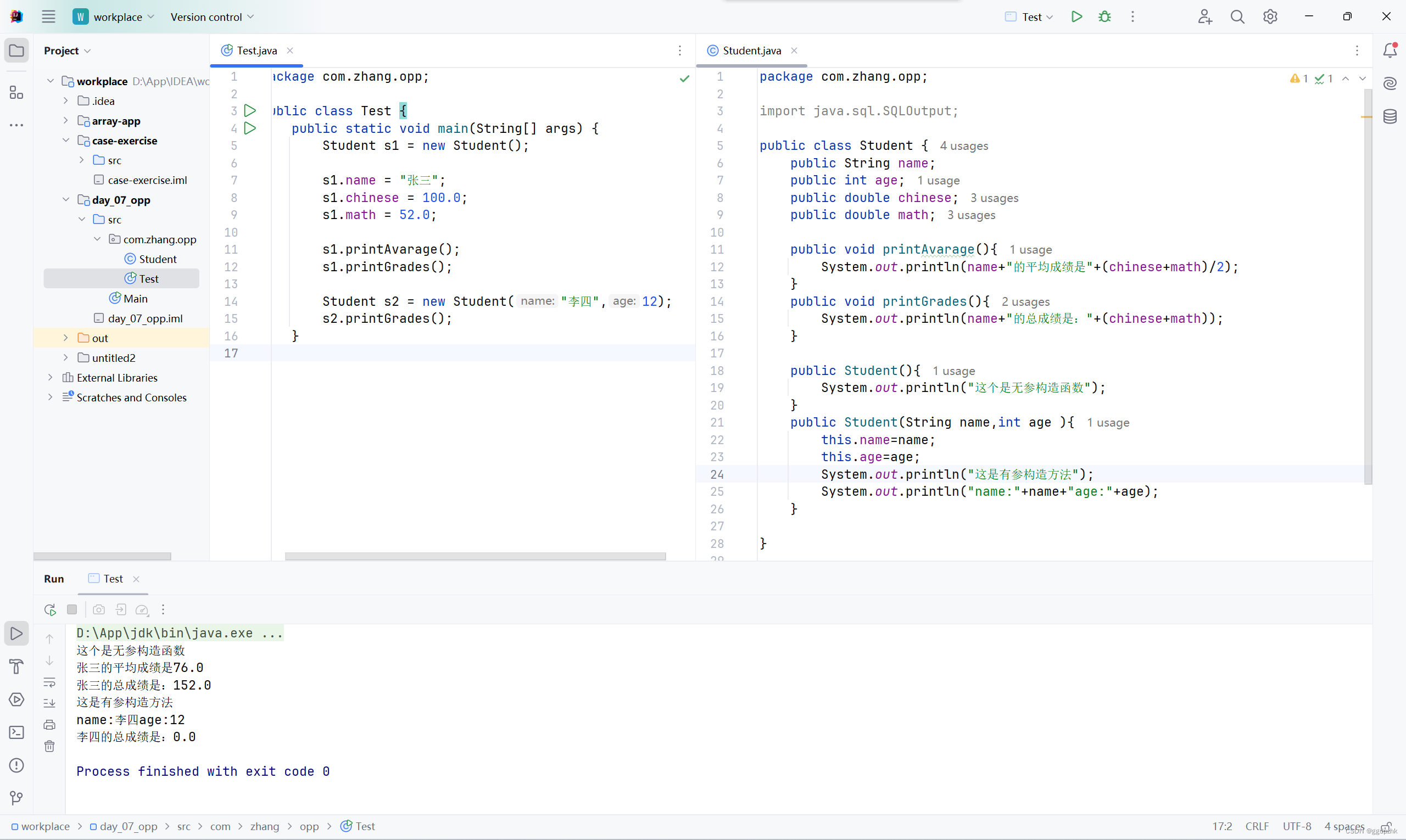
ArrayList

ArrayListclass和LinkedList类是List接口的具体实现

 A list can grow or shrink dynamically
While an array is fixed once it is created

LinkedList

Node

Each node contains an element/value, and each node is linked to its next neighbor:

Node 也可以单独被定义成一个类

get(i)

get(i)方法可用于链表，但是查找每个元素是一个更耗时的操作

相反，你应该使用Iterator或for-each循环:

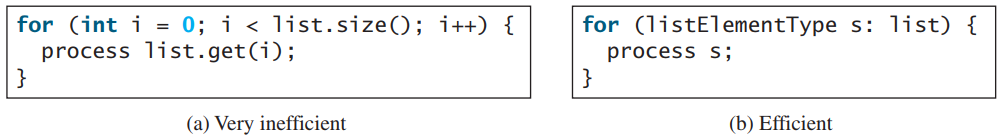
ArrayList vs LinkedList

    If you need to support random access through an index without inserting or removing elements from any place other than the end, ArrayListoffers the most efficient collection

如果您需要支持通过索引的随机访问，而不需要从末尾以外的任何位置插入或删除元素

    If your application requires the insertion or deletion of elements from at the beginning of the list, you should choose LinkedList

如果您的应用程序需要插入或删除列表开头的元素

Comparator Interface Comparator

 want to compare the elements that are not instances of Comparable or by a different criteria than Comparable → define Comparator →Define a class that implements the java.util.Comparator<T> interface

（参考代码）

Static methods

max, min, disjoint, and frequency methods for collections
sort, binarySearch, reverse, shuffle, copy, and fill methods for lists

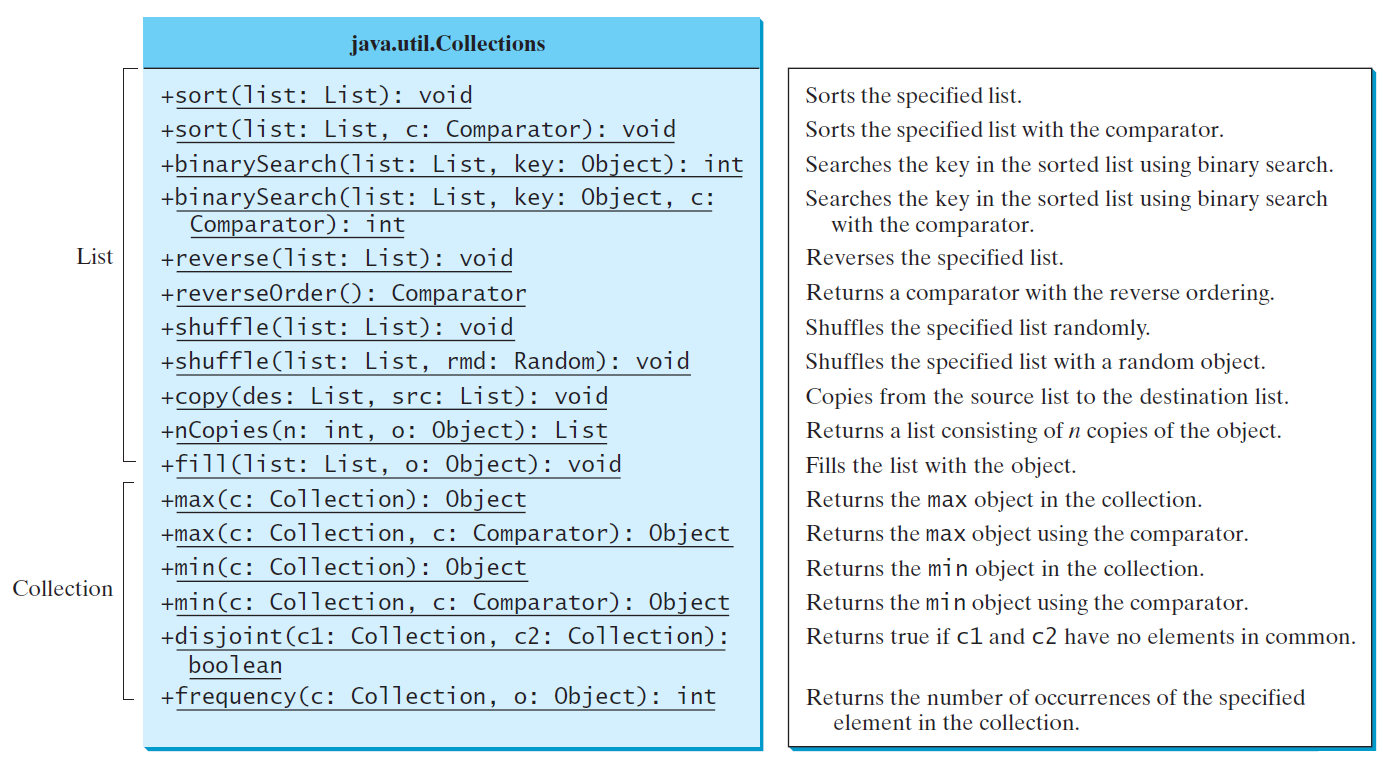
for List

1. Sorting:

Collections.sort(list);

To sort it in descending order, you can simply use the Collections.reverseOrder()

2. Binary search:

Collections.binarySearch(list1,7));

    To use this method, the list must be sorted in increasing order
    If the keyis not in the list, the method returns -(insertion point + 1)

for List and Collections

1. Reverse:

Collections.reverse(list);

2. Shuffle:

Collections.shuffle(list);

3.Copy:

Collections.copy(dest, src);

copy all the elements from a source list to a destination list on the same index(注意是同索引！！！其它元素不变！！！)

The copymethod performs a shallow copy: only the references of the elements from the source list are copied

4. Arrays.asList()

provides the static asList method for creating a list from a variable-length list of arguments

java.util.Arrays$ArrayList, which is also called ArrayList but it is just a wrapper for an array 

5. nCopies(int n, Object o)

创建由指定对象的n个副本组成的不可变列表

由 nCopies method创建的列表是不可变的，所以你不能在列表中添加/删除元素——所有的元素都有相同的引用!

List<String> list = Collections.nCopies(5, "A"); //list={"A", "A", "A", "A", "A"}
// 尝试修改列表会抛出异常
list.add("B"); // UnsupportedOperationException

6. fill(List list, Object o)

Arrays.asList("red","green","blue"); 、

Collections.fill(list, "black");   // [black, black, black]

7. max & min

find the maximum and minimum elements in a collection

Collections.max(collection)

Collections.min(collection)

8.disjoint(collection1, collection2)

returns trueif the two collections have no elements in common

9. frequency(collection, element)

method finds the number of occurrences of the elementin the collection

Vector 

这些类被重新设计以适应Java Collections Framework，但为了兼容性保留了它们的旧风格方法

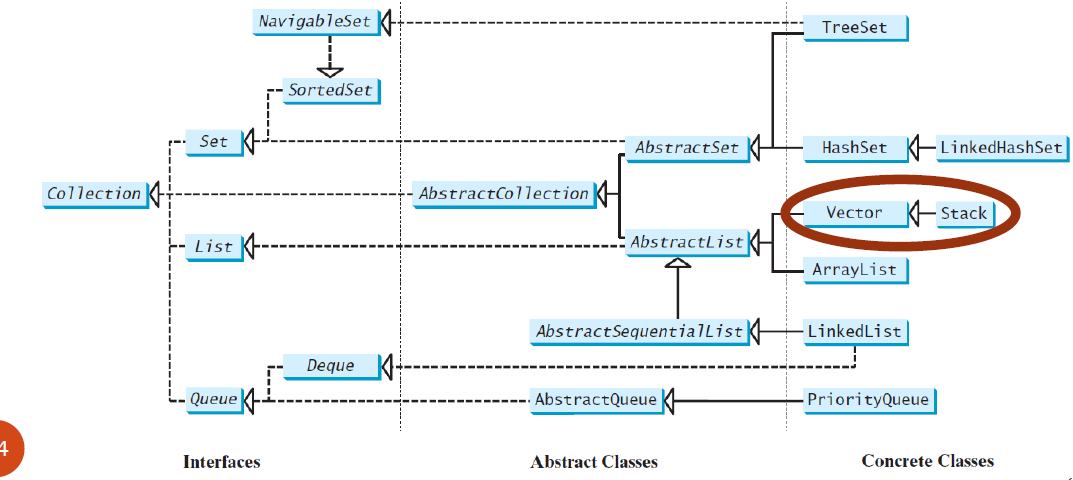
vector与ArrayList相同，除了包含访问和修改vector的synchronizedmethods

• 同步：Vector 是同步的，这意味着它是线程安全的。多个线程可以同时访问一个 Vector 实例而不会引发并发问题。这是 Vector 与 ArrayList 的一个主要区别，ArrayList 不是同步的。
• 动态调整大小：与数组不同，Vector 的大小是可动态调整的。当需要时，它会自动扩展以适应添加的新元素。
• 实现接口：Vector 实现了 List、RandomAccess、Cloneable 和 Serializable 接口，这使得它具有列表的特性，可以快速随机访问，可以克隆和序列化。

For many applications that do not require synchronization, using ArrayListis more efficient than using Vector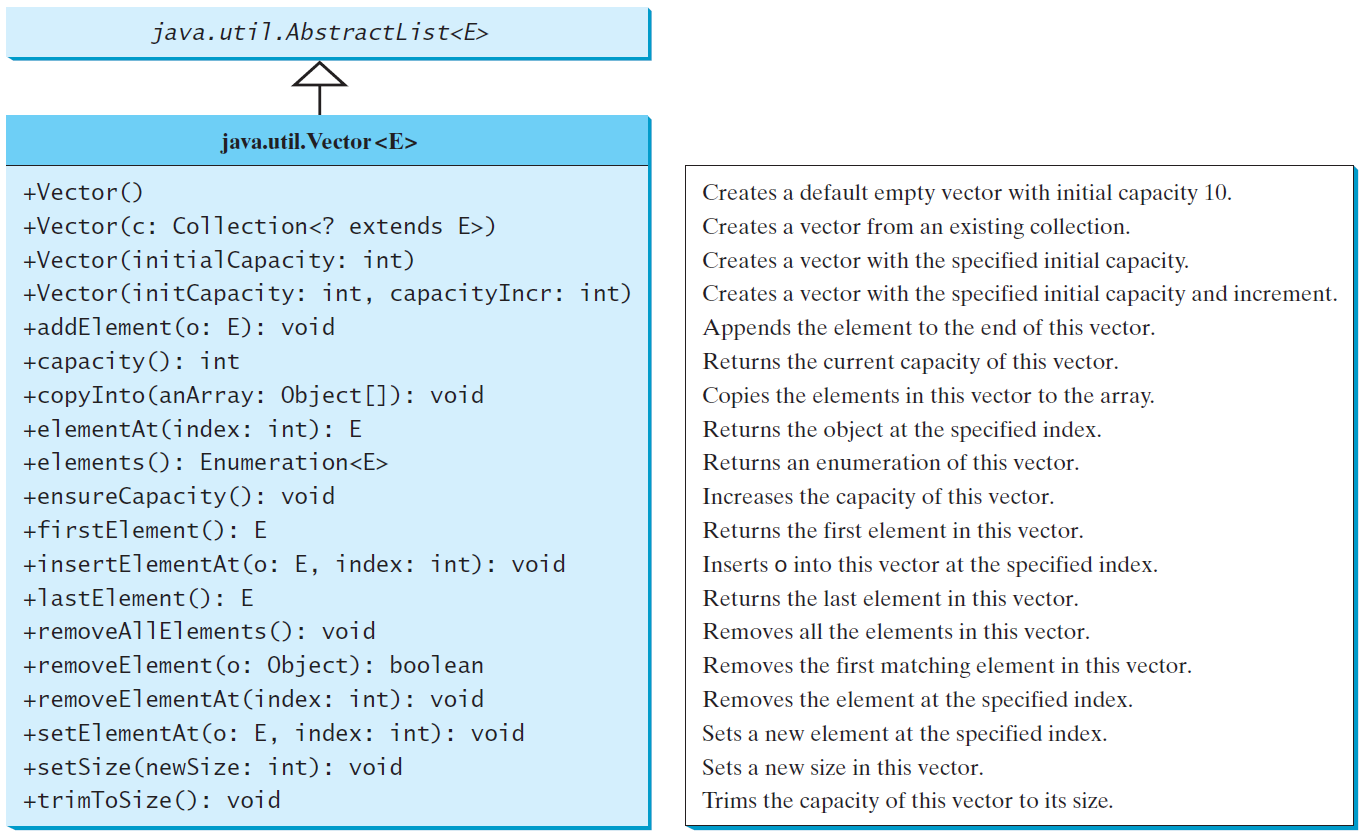

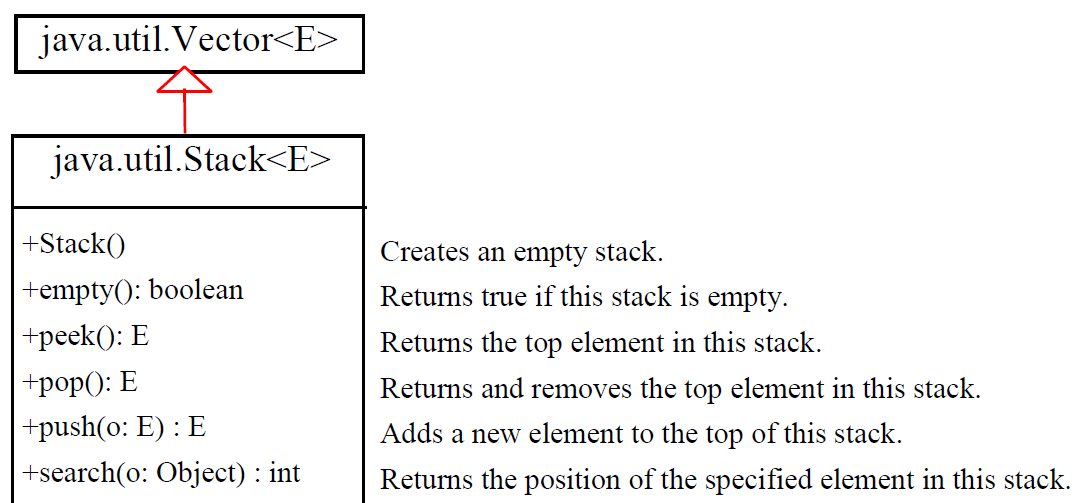
Stack

The Stackclass represents a last-in-first-out stack of objects
元素只能从堆栈顶部访问

您可以使用push(o:E)插入，使用peek()检索和使用pop()删除(都来自堆栈顶部)

堆栈作为Vector的扩展实现

从Java 2保留的方法:empty()方法与isEmpty()相同

Queues and Priority Queues

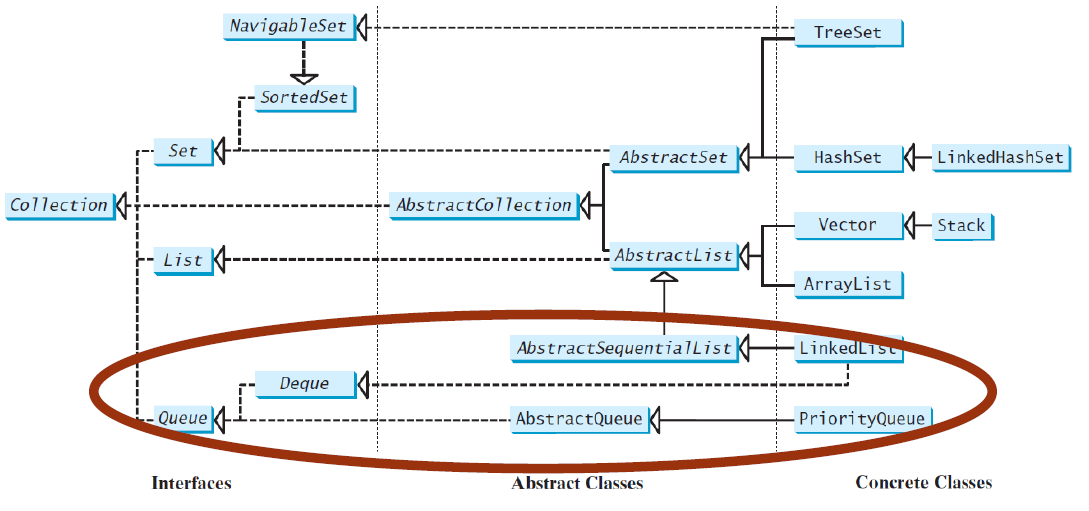
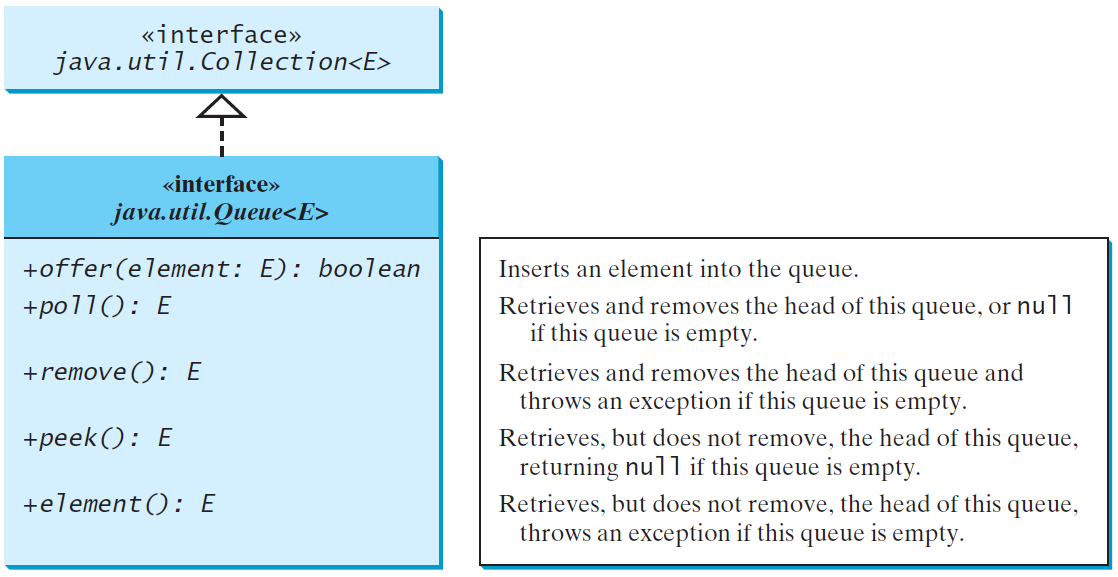
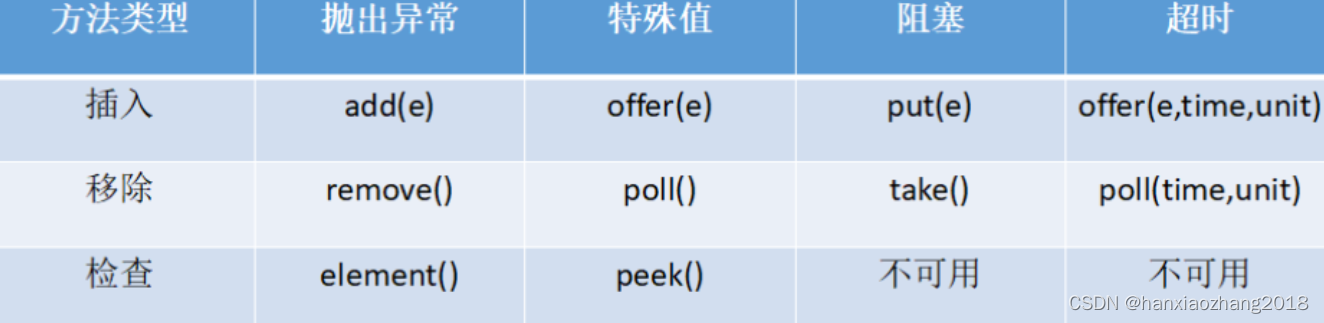
A queue is a first-in/first-out data structure: Elements are appended to the end of the queue and are removed from the beginning of the queue
    The offer(o:E) method is used to add an element to the queue
    This method is similar to the addmethod in the Collection interface, but the offer method is preferred for queues
    The poll and remove methods are similar, except that poll() returns null if the queue is empty, whereas remove()throws an exception
    The peek and element methods are similar, except that peek() returns null if the queue is empty, whereas element()throws an exception
 

Queue interface extends java.util.Collection with additional insertion, extraction, and inspection operations 

Using LinkedList for Queue

The LinkedListclass implements the Dequeinterface, which extends the Queueinterface

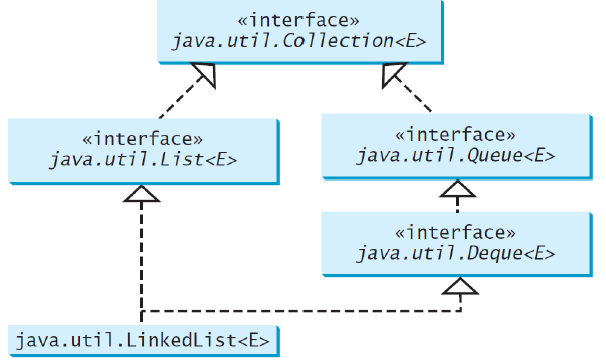
Deque(“double-ended queue”) interface supports element insertion and removal at both ends

    The Deque interface extends Queue with additional methods for inserting and removing elements from both ends of the queue
    The methods addFirst(e), removeFirst(), addLast(e), removeLast(), getFirst(), and getLast()are defined in the Deque interface

LinkedList is the concrete class for queue and it supports inserting and removing elements from both ends of a list

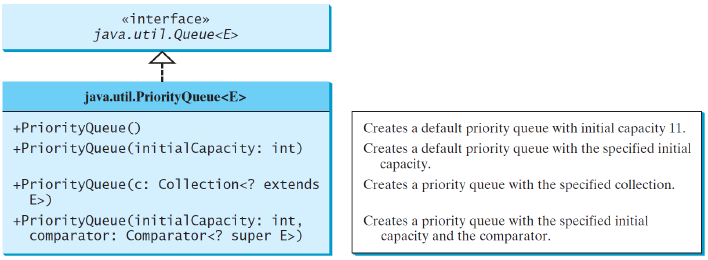
priority queue

In a priority queue, elements are assigned priorities
When accessing elements, the element with the highest priority is removed first

在优先级队列中，元素被分配优先级。访问元素时，优先级最高的元素首先被删除

To use stacks to write a program to evaluate expressions**

W7 - Sets and Maps

Set

The concrete classes that implement Set must ensure that no duplicate elements can be added to the set
●    HastSet & LinkedHashSet use: hashcode() + equals()
●    TreeSet use: compareTo() or Comparable

HashSet

Ordering: It does not guarantee any order of iteration.
Internal Structure: Backed by a hash table.
 

creation

Set<String> set = new HashSet<>();

●    The first diamond operation ("<>") is called a type parameter or generic type. It specifies the type of elements that the HashSet will store. In this case, the HashSet is specified to store objects of type Integer.
●    In the 2nd diamond operation ("<>"),the compiler infers the generic type from the context, which is typically the same as the type specified in the first diamond operator (Just in simple cases)
●    The parentheses ("()") is used for calling the constructor of the HashSet class. In this case, it is calling the no-argument constructor of the HashSet class, which creates an empty set.

2）The HashSet class is concrete class 具体类  that implements Set

3） 3 and 4. You can an empty HashSet with the specified initial capacity only (case 3) or initial capacity plus loadFactor (case 4)

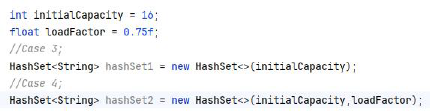
初始容量InitialCapacity和负载因子loadFactor

• 初始容量：HashSet 在创建时可以指定初始容量，即哈希表中桶的数量。默认初始容量是16。
• 负载因子：负载因子是一个介于0和1之间的数值，用于衡量集合在自动增加其容量之前可以填充的程度。默认负载因子是0.75，这意味着当哈希表中的元素数量达到桶数量的75%时，哈希表将会进行扩容。

method

接口(如Collection)和抽象类(如AbstractSet)将由 concrete classes(如HashSet、LinkedHashSet、TreeSet)实现/扩展。因此，所有声明的方法(例如，add()， remove()等)都可以在set实例中调用。

1)add()

unordered:ecause of hashing, W13

no-duplicated:

●    A hash set use hashcode() and equals() to check duplication
●    These 2 methods are "built-in" in the String object, as they are part of the standard String class in Java (Same as other objects from the standard Java library like Integer)

遍历

iterable，但是可以用for循环

Way 1: Enhanced for loop

Way 2: forEach()

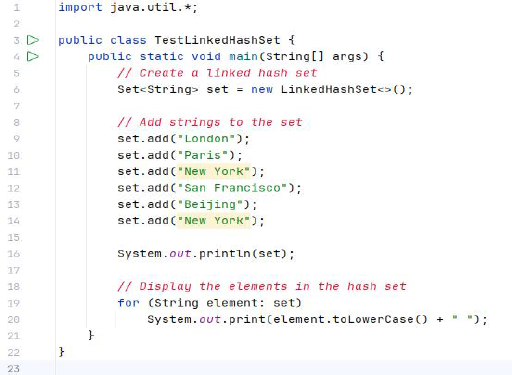
Linked HashSet

Ordering: Maintains a doubly-linked list running through all its entries, which defines the iteration ordering, which is normally the order in which elements were inserted into the set (insertion-order). 维护一个遍历其所有条目的双链表，它定义了迭代排序，这通常是元素插入集合的顺序(插入顺序)。
 Internal Structure: Backed by a hash table with a linked list running through it

●    LinkedHashSet extends HashSet with a linked list implementation that supports an ordering of the elements in the set
Significant Difference: The elements in a LinkedHashSet can be retrieved in the order in which they were inserted into the set

TreeSet

Ordering: Guarantees that elements will be sorted in ascending element order, according to the natural ordering of the elements, or by a Comparator provided at set creation time.
Internal Structure: Backed by a tree

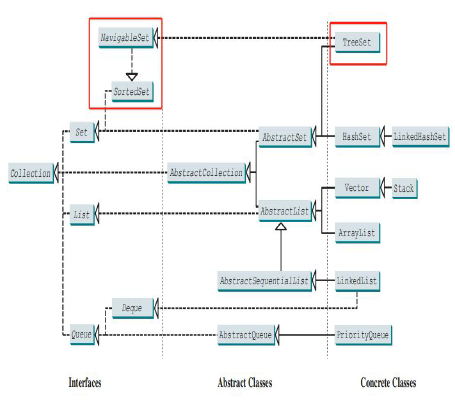
●    TreeSet is a concrete class that implements the SortedSet and NavigableSet interfaces

SortedSet is a sub-interface of Set,which guarantees that the elements in the set are sorted 

NavigableSet extends SortedSet to provide navigation methods  (e.g., lower(e), floor(e),etc)

creation

●    Empty tree set without arguement, which will be sorted in ascending order according to the natural ordering of its elements. (Due to the implementation of SortedSet interface)
        TreeSet<String> treeSet = new TreeSet<>();

●    Tree set with other collections, being sorted by the natural ordering.
        TreeSet<String> treeSet = new TreeSet<>(list)

●    Tree set with customized comparator,where we can define the orders
        TreeSet<String> treeSet = new TreeSet<>(Comparator.reverseOrder())

●    Tree set with the same elements and the same ordering as the specified sorted set
        // If we already have a set sorted according to a specific rule
        SortedSet<String> originalSet = new TreeSet<>(String.CASE_INSENSITIVE_ORDER);

        // We take this way to create another tree set with same elements and same ordering         TreeSet<String> copiedSet = new TreeSet<>(originalSet);

Method

1. add()

不能重复：不是hashcode()和equals()，这是因为Java标准库中的String和Integer以及其他包装器类中的“内置”compareTo()

差异是由于底部的数据结构，哈希集->哈希(W13)，树集->树(11&12)。

hash set -> Hashing (W13), tree set -> Tree (11&12).

first(): return the first element in the set

last(): return the last element in the set

headSet(): find the elements that are less than or equal to the given toElement (i.e., “New York”)

tailSet(): find the elements that are equal to or bigger than the given toElement (i.e., “New York”)

lower(): Returns the greatest element in this set strictly less than the given element (4)

higher(): Returns the least element in this set strictly greater than the given element (?)

floor(): Returns the greatest element in this set less than or equal to the given element (5)

ceiling(): Returns the least element in this set greater than or equal to the given element (?)

pollFirst(): Retrieves and removes the first (lowest) element

pollLast(): Retrieves and removes the last (highest) element

Set vs List

Sets are more efficient than lists for storing non duplicate elements,无索引，通过for each遍历
 Lists are useful for accessing elements through the index
 

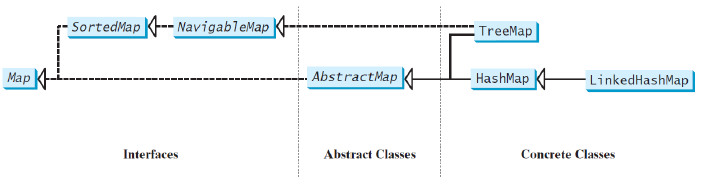
Map

A map is a container object that stores a collection of key/value pairs.
It enables fast retrieval, deletion, and updating of the pair through the key. A map stores the values along with the keys.
●    In List, the indexes are integers. In Map, the keys can be any objects.
        A map cannot contain duplicate keys.
        Each key maps to one value.

The HashMap, LinkedHashMap, and TreeMap classes are three concrete implementations of the Map interface, with TreeMap additionally implements SortedMap and NavigableMap

they ensure the map instances non-duplicated using hashcode() and equals()(for HashMap and LinkedHashMap) as well as the compareTo()/Comparator (for TreeMap).
 

create

m: Map<? extends K,? extends V>

它表示构造函数接受Map <X，Y>(即smallMap)，其中X是K的子类，Y是V的子类(见图)。It would also work when X is exactly K, and Y is exactly V
e.g

Map<Integer, String> smallMap = new HashMap<>();

Map<Integer, String> largerMap = new HashMap<>(smallMap);

通常，与LinkedHashSet类似，LinkedHashMap扩展了HashMap的链表实现，支持按insertion order 检索元素。

In LinkedHashMap, there is a constructor arguement (initialCapacity: int, loadFactor: float, accessOrder: boolean)

Once it is set to be  LinkedHashMap(initialCapacity, loadFactor, true), the created LinkedHashMap would allow us to retreive elements  in the order in which they were last accessed 按照它们最后一次被访问的顺序, from least recently to most recently accessed (access order).

Method

•    A hash map is unordered, similar to a hash set
•    A tree map is ordered by the keys of the involved elements (alphabetically in this case)
•    A  linked hash map can be ordered by the insertion order, and by the access order (accessOrder: True)
 

get(): Returns the value to which the specified key is mapped

forEach():Performs the given action for each entry in this map until all entries have been processed or the action throws an exception.

W8-Developing Efficient Algorithms

    To estimate algorithm efficiency using the Big O notation
    To explain growth rates and why constants and non-dominating terms can be ignored
    To determine the complexity of various types of algorithms
    To analyze the binary search algorithm
    To analyze the selection sort algorithm
    To analyze the insertion sort algorithm
    To analyze the Tower of Hanoi algorithm
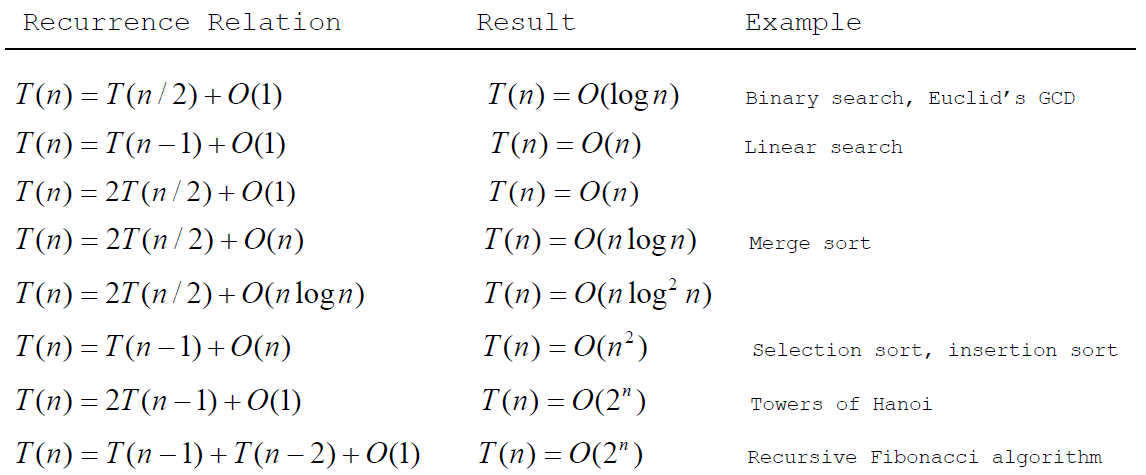
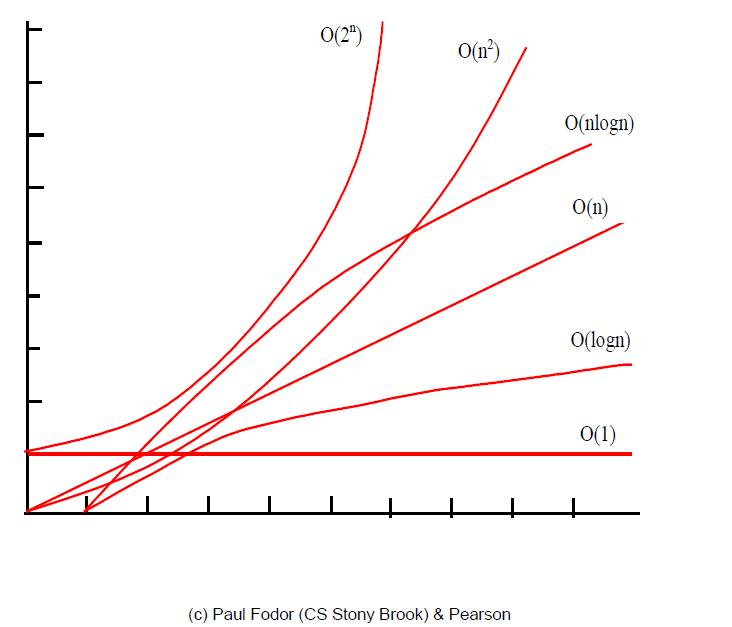
    To describe common growth functions (constant, logarithmic, linear, log-linear, quadratic, cubic (polynomial), exponential)
    To design efficient for finding Fibonacci numbers using dynamic programming
    To design efficient algorithms for finding the closest pair of points using the divide-and-conquer approach

Big O notation

used to measure the execution time (named time complexity)

Space complexity measures the amount of memory space used by an algorithm, can also be measured using Big-O(然而我们讲座中大多数都是O(n))

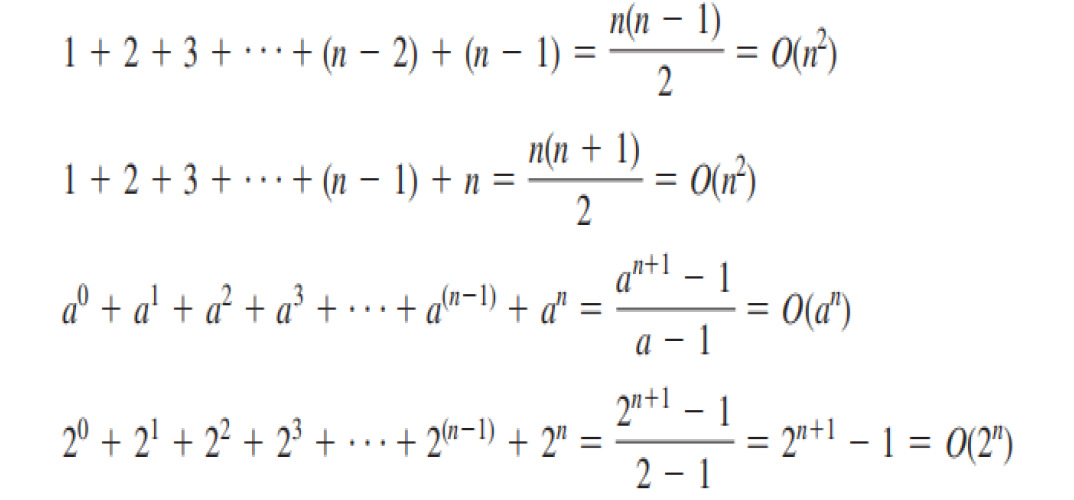
complexity of various types of algorithms

Simple Loops O(n)

Nested Loops O(n^2)

Sequence O(n)

Selection  O(n)

Logarithmic time O(log n)

Binary search O(logn)

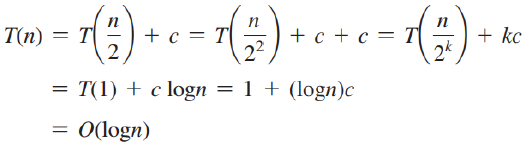
Selection Sort O(n^2)

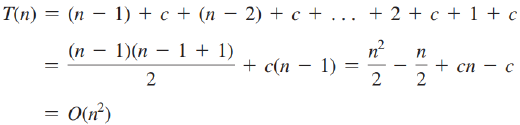
InsertionSort O(n^2)

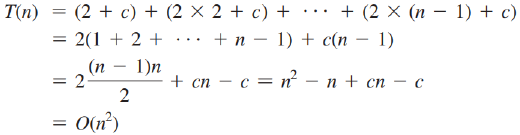
Tower of Hanoi O(2^n)

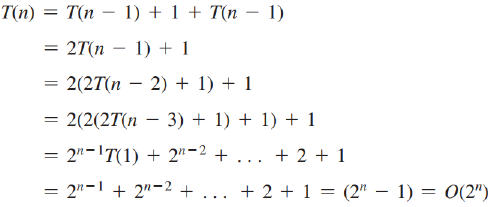
Fibonacci Numbers O(2^n) vs O(n)

common growth functions 

 

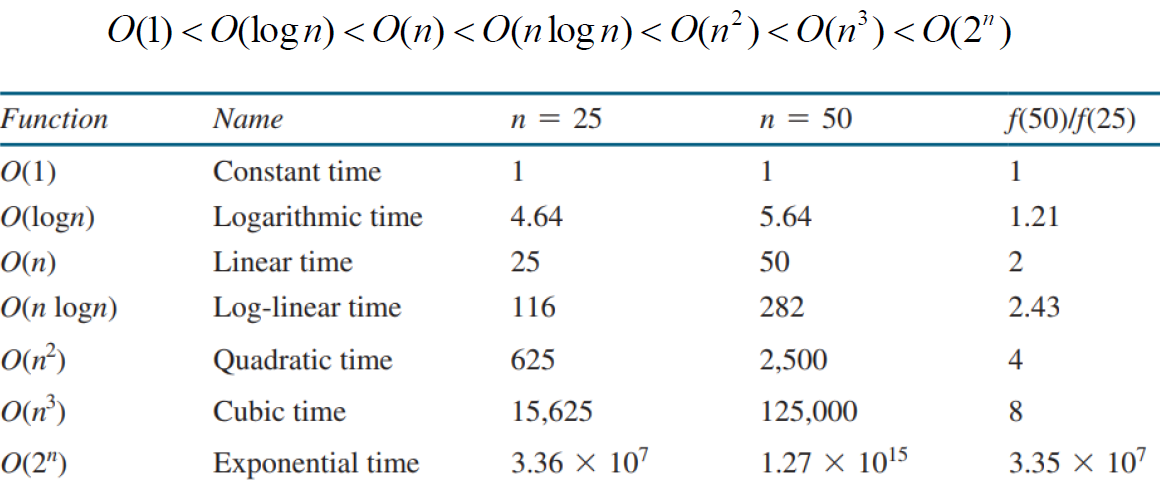
Algorithm Design

1.    Problem definition
2.    Development of a model
3.    Specification of the algorithm
4.    Designing an algorithm
5.    Checking the correctness of the algorithm
6.    Analysis of algorithm
7.    Implementation of algorithm
8.    Program testing
9.    Documentation preparation

Techniques

Brute-force or exhaustive search 穷举

the naive method of trying every possible solution to see which is best.

Divide and conquer 分而治之

repeatedly reduces an instance of a problem to one or more smaller instances of the same problem (usually recursively) until the instances are small enough to solve easily.

divides the problem into subproblems, solves the subproblems, then combines the solutions of subproblems to obtain the solution for the entire problem.

don't overlap

e.gClosest Pair of Points

Dynamic programming 动态规划

hen the same subproblems are used to solve many different problem instances, dynamic programming avoids recomputing solutions that have already been computed.

The key idea behind dynamic programming is to solve each subprogram only once and store the results for subproblems for later use to avoid redundant computing of the subproblems

Greedy algorithms 贪心算法

follow the problem-solving heuristic of making the locally optimal choice at each stage.

Backtracking 回溯法

multiple solutions are built incrementally and abandoned when it is determined that they cannot lead to a valid full solution.

e.g 八皇后问题

    To design efficient for finding Fibonacci numbers using dynamic programming
    To design efficient algorithms for finding the closest pair of points using the divide-and-conquer approach

W9 - Sorting

    To study and analyze time complexity of various sorting algorithms
    To design, implement, and analyze bubble sort
    To design, implement, and analyze merge sort
    To design, implement, and analyze quick sort
    To design and implement a binary heap
    To design, implement, and analyze heap sort
    To design, implement, and analyze insertion sort

bubble sort

Since the number of comparisons is n - 1 in the first pass, the best-case time for a bubble sort is O(n). worst case O(n^2)

The pass through the list is repeated until no swaps are needed, which indicates that the list is sorted 优化：如果一次排序中没有发生交换，则不需要进行下一次排序了
 

merge sort

divide and conquer algorithm

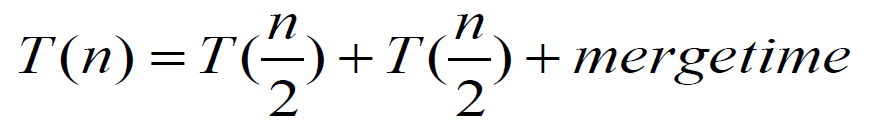
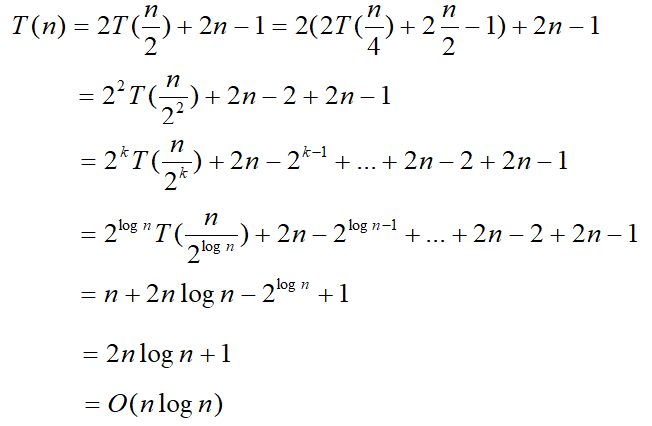
quick sort

基本思想：

选定pivot中心轴

将大于pivot的数字放在pivot的右边

将小于pivot的数字放在pivot的左边

分别堆左右子序列重复前三步操作

base case: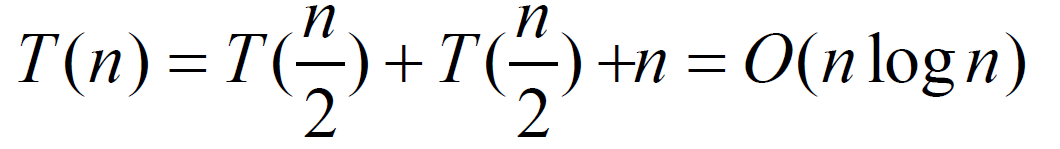

worst case: O(n^2)

Divides/partitions

binary heap

h = log n

add

O(n log n) 

remove

O(n log n) 

Heap Sort Time: O(n log n)

heap sort

Insertion Sort

The insertion sort algorithm sorts a list of values by repeatedly inserting an unsorted element into a sorted sublist until the whole list is sorted. 

W10-1 - Graphs and Applications

    To model real-world problems using graphs
    Explain the Seven Bridges of Königsberg problem
    To describe the graph terminologies: vertices, edges, directed/undirected, weighted/unweighted, connected graphs,  loops, parallel edges, simple graphs, cycles, subgraphs and spanning tree
    To represent vertices and edges using edge arrays, edge objects, adjacency matrices, adjacency vertices list and adjacency edge lists
    To model graphs using the Graphinterface, the AbstractGraph class, and the UnweightedGraphclass
    To represent the traversal of a graph using the
AbstractGraph.Tree
    To design and implement depth-first search
    To solve the connected-component problem using depth-first search
    To design and implement breadth-first search

graph terminologies

A graph G = (V, E),where Vrepresents a set of vertices (or nodes) and Erepresents a set of edges (or links). A graph may be undirected (i.e., if (x,y) is in E, then (y,x) is also in E) or directed

Adjacent Vertices：

Two vertices in a graph are said to be adjacent (or neighbors) if they are connected by an edge.An edge in a graph that joins two vertices is said to be incident to both vertices

Degree:

The degree of a vertex is the number of edges incident to it

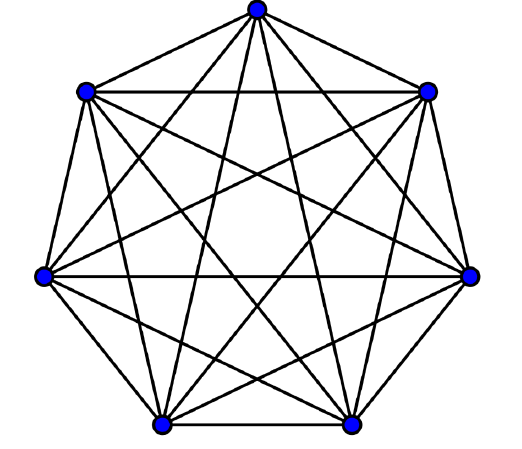
Complete graph:

every two pairs of vertices are connected

Incomplete graph: 

parallel edge

If two vertices are connected by two or more edges, these edges are called parallel edges

loop:

is an edge that links a vertex to itself

simple graph:

is one that has doesn’t have any parallel edges or loops

Connected graph:

A graph is connected if there exists a path between any two vertices in the graph

任意一对节点之间都存在至少一条路径的图。这意味着从图中的任何一个节点出发，可以通过边到达图中的任何其他节点。

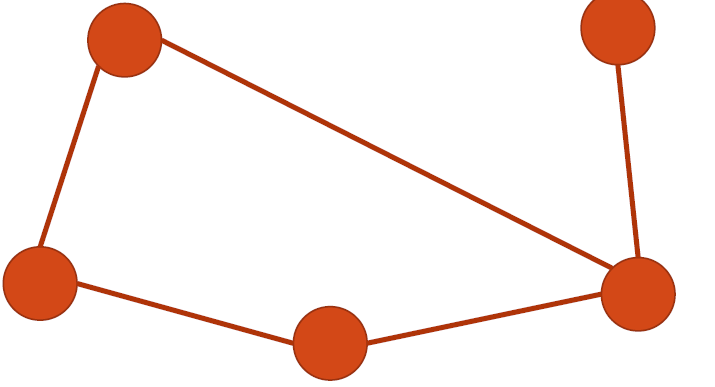
Tree：

A connected graph is a tree if it does not have cycles

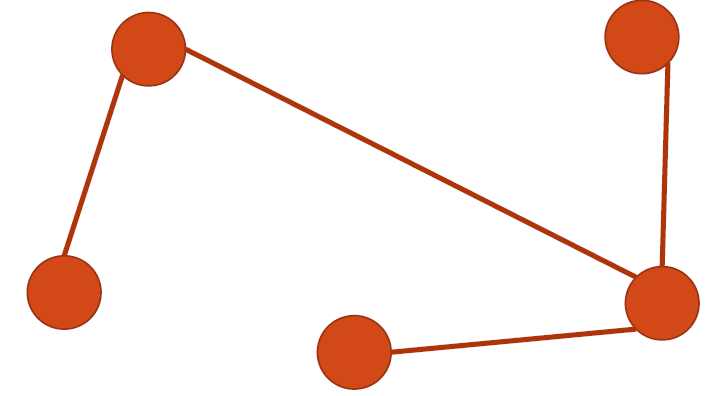
closed path:

 a path where all vertices have 2 edges incident to them

Cycle:

a closed path that starts from a vertex and ends at the same vertex

cycle vs closed path

• 节点重复：在环中，节点不能重复出现（除了起点和终点重合），而在闭路径中，节点可以重复访问，但必须通过不同的边。
• 普遍性：环是闭路径的一个特例。所有的环都是闭路径，但并非所有的闭路径都是环。

subgraph：

A subgraph of a graph G is a graph whose vertex set is a subset of that of G and whose edge set is a subset of that of G

Spanning Tree

A spanning tree of a graph G is a connected subgraph of G and the subgraph is a tree that contains all vertices in G

Representing Graphs

Representing Vertices
Representing Edges: Edge Array
Representing Edges: Edge Objects

（感觉上面的用不太到）
Representing Edges: Adjacency Matrices

int[][] adjacencyMatrix = {}把表列出来

Representing Edges: Adjacency Lists

List<List<Integer>> neighbors =  = new ArrayList();

这里细节就看ppt了

Modeling Graphs

The Graph interface defines the common operations for a graph
An abstract class named AbstractGraphthat partially implements the Graphinterface

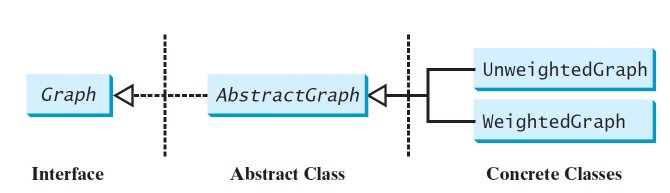
traversal of a graph

DFS

BFS
 

DFS Application

1） Detecting whether a graph is connected
        Search the graph starting from any vertex
        If the number of vertices searched is the same as the number of vertices in the graph, the graph is connected. Otherwise, the graph is not connected.

2） Detecting whether there is a path between two vertices AND find it (not the shortest)
       Search the graph starting from one of the 2 vertexes
       Check if the second vertex is reached by DFS

3） Finding all connected components:找出图中的所有连通分量
 A connected component is a maximal connected subgraph in which every pair of vertices are connected by a path
Label all vertexes as unreached
Repeat until no vertex is unreached
Start from any unreached vertex and compute DFS
(marking all reached vertexes, including the first vertex, as reached) -> this DFS is one connected component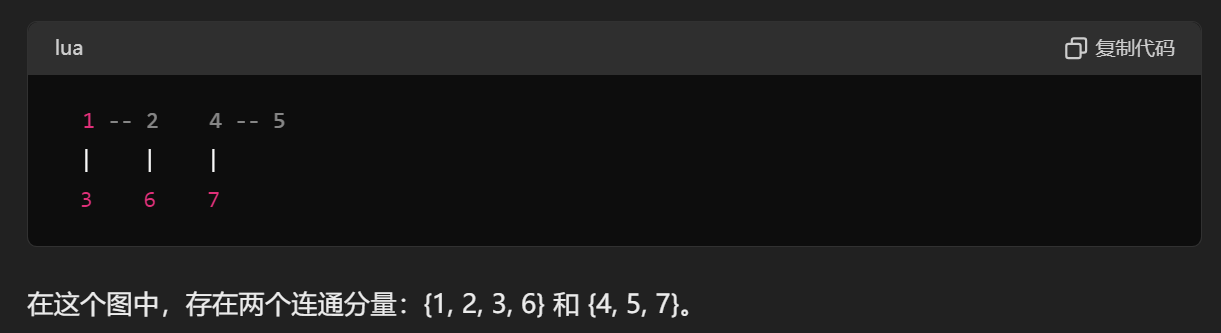

 

BFS Application

1） Detecting whether a graph is connected (i.e., if there is a path between any two vertices in the graph)
       check is the size of the spanning tree is the same with the number of vertices

2）Detecting whether there is a path between two vertices
         Compute the BFS from the first vertex and check if the second vertex is reached

3）Finding a shortest path between two vertices
We can prove that the path between the root and any node in the BFS tree is the shortest path between the root and that node

4)  Finding all connected components

5)  Detect whether there is a cycle in the graph by modifying BFS (if a node was seen before, then there is a cycle - you can also extract the cycle)

6)  Testing whether a graph is bipartite（二部图）(顶点染色问题)

一个图是二部图（Bipartite Graph），当且仅当其顶点集可以被划分为两个不相交的子集 U 和 V，使得图中的每一条边都连接一个来自 U 的顶点和一个来自 V 的顶点。换句话说，二部图的顶点可以被着色为两种颜色，使得每条边的两个端点的颜色不同。

A graph is bipartite if the vertices of the graph can be divided into two disjoint sets such that no edges exist between vertices in the same set
A graph is bipartite graph if and only if it is 2-colorable.

While doing BFS traversal, each node in the BFS tree is given the opposite color to its parent.
  If there exists an edge connecting current vertex to a previously-colored vertex with the same color, then we can safely conclude that the graph is NOT bipartite.

If the graph is bipartite, then one partition is the union of all odd number stratas, while another is the union of the even number stratas

W10-2 Weighted Graphs and Applications

    To represent weighted edges using adjacency matrices and adjacency lists
    To model weighted graphs using the WeightedGrap hclass that extends the AbstractGraph class
    To design and implement the algorithm for finding a minimum spanning tree
    To define the MST class that extends the Tree class
    To design and implement the algorithm for finding single-source shortest paths
    To define the ShortestPathTreeclass that extends the Tree class

 A graph is a weighted graph if each edge is assigned a weight

Representing Weighted Graphs 

Edge Array

Weighted Adjacency Matrices

Adjacency Lists

Modeling Weighted Graphs

finding a minimum spanning tree

 A minimum spanning tree is a spanning tree (i.e., a subset of the edges of a connected undirected graph that connects all the vertices together without any cycles) with the minimum total weight

e.g create wired Internet lines

sol: Prim’s Algorithm

MST class that extends the Tree class

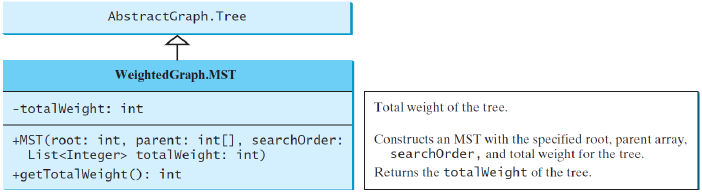
finding single-source shortest paths

Find a shortest path between two vertices in the graph
The shortest path between two vertices is a path with the minimum total weight
e.g  Dijkstra, 

ShortestPathTree class that extends the Tree class

W11 Binary Search Trees

    To design and implement a binary search tree
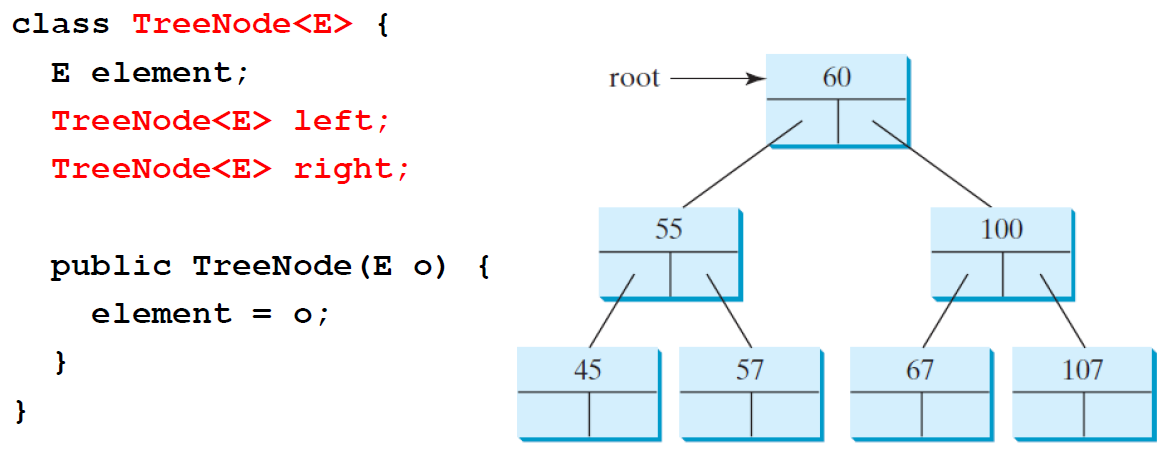
    To represent binary trees using linked data structures
    To insert an element into a binary search tree
    To search an element in binary search tree
    To traverse elements in a binary tree
    To delete elements from a binary search tree
    To create iterators for traversing a binary tree
    To implement Huffman coding for compressing data using a binary tree

A binary tree is a hierarchical structure: it is either empty or consists of an element, called the root, and two distinct binary trees, called the left subtree and right subtree
 

Representing 

Binary Trees

linked nodes

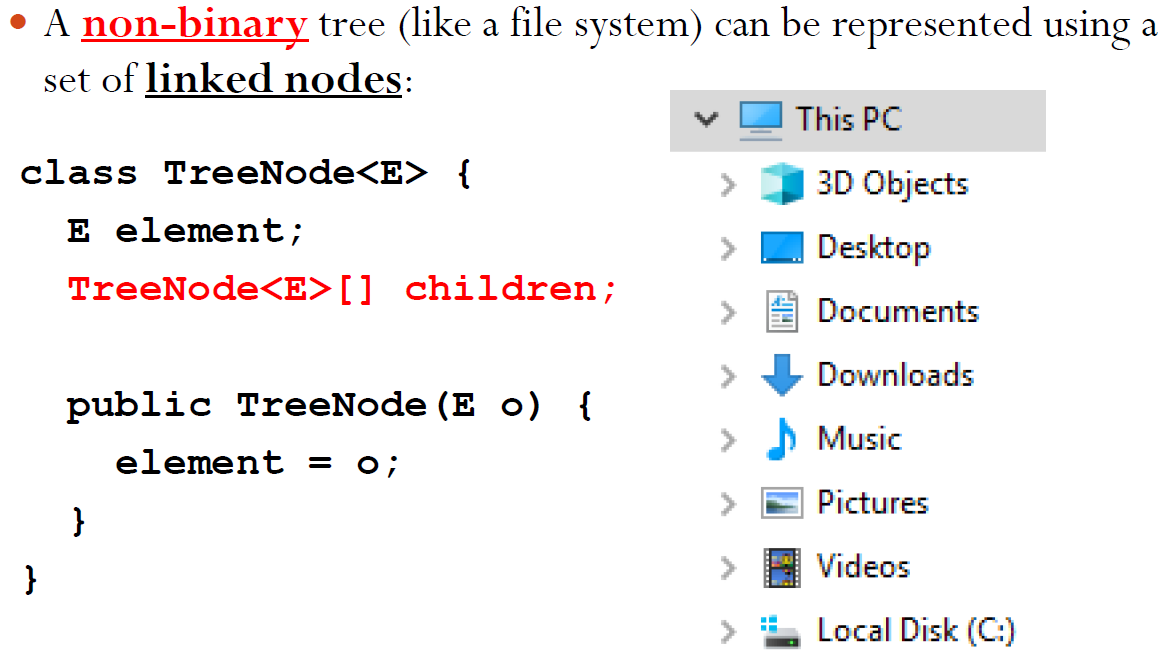
Non-Binary Trees

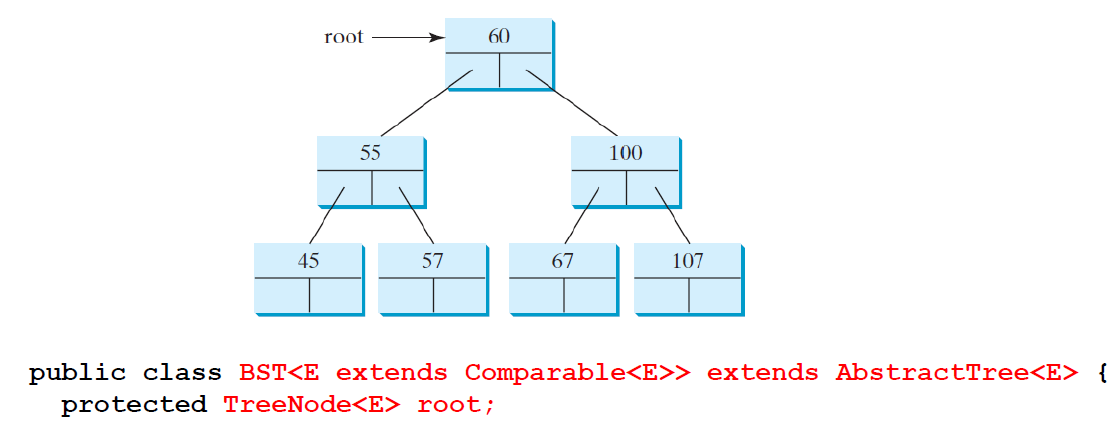
Binary Search Tree

A special type of binary trees, called binary search tree is a binary tree with no duplicate elements and the property that for every node in the tree the value of any node in its left subtree is less than the value of the node and the value of any node in its right subtree is greater than the value of the node（左子树上所有节点的值都小于根节点的值。右子树上所有节点的值都大于根节点的值。）

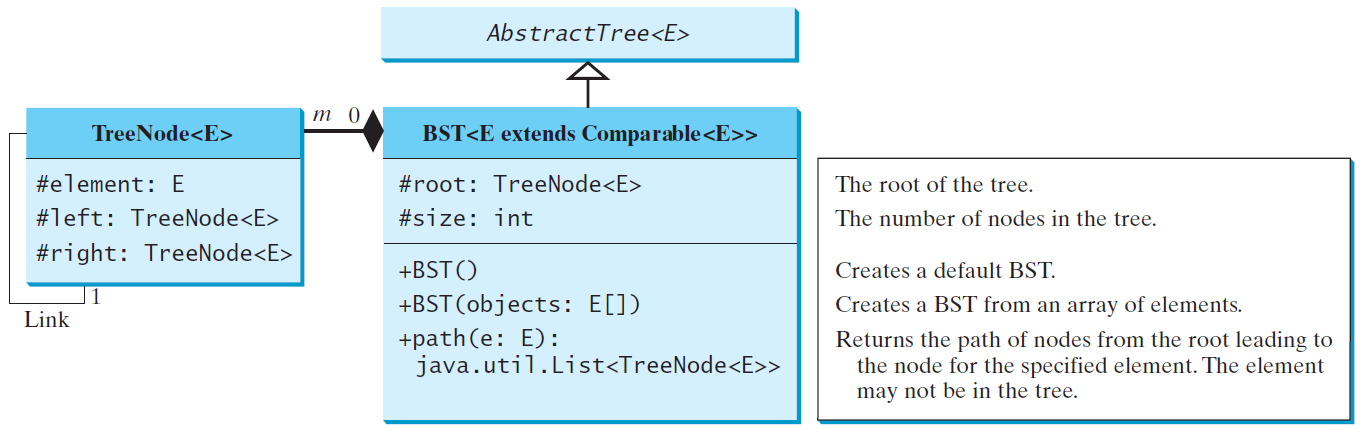
Inserting

看ppt

Traversal

process of visiting each node in the tree exactly once

方法：

preorder, inorder, postorder, depth-first, breadth-first

Tree Interface

Delete

看ppt

Complexity

inorder, preorder, and postorder traversals is O(n)

The time complexity for search, insertion and deletion is the height of the tree
In the worst case, the height of the tree is O(n)

Iterator

    The iterator method for Treereturns an instance of InorderIterator
    The InorderIterator constructor invokes the inorder method that stores all the elements from the tree in a list

The hasNext() method checks whether currentis still in the range of list.
Invoking the next() method returns the current element and moves currentto point to the next element in the list.
The remove() method removes the current element from the tree and a new list is created -current does not need to be changed.

Huffman coding implementation

补代码！

Huffman 编码是一种用于数据压缩的算法，由大卫·霍夫曼（David A. Huffman）于1952年提出。它利用不同字符的出现频率来构建可变长度的编码，以便将出现频率较高的字符用较短的编码表示，从而达到压缩数据的目的。

这个算法的核心思想是构建一颗 Huffman 树（Huffman Tree），通过该树来生成每个字符的编码。

W12 AVL Trees

    To know what an AVL tree is
    To understand how to balance a tree using the LL rotation, LR rotation, RR rotation, and RL rotation
    To knowhow to design the AVLTreeclass
    To insert elements into an AVL tree
    To implement node rebalancing
    To delete elements from an AVL tree
    To implement and test the AVLTreeclass
    To analyze the complexity of search, insert, and delete operations in AVL trees
 

Complexity

The search, insertion, and deletion time for a binary search tree is dependent on the height of the tree

In the worst case, the height is O(n), so worse time  complexity is O(n)

If a tree is perfectly balanced, i.e., a complete binary tree, its height is log n,So, search,insertion, and deletion time would be O(log n)

balance

you may have to rebalance the tree after an insertion or deletion operation

The balance factor of a node is the height of its right subtree minus the height of its left subtree

A node is said to be balanced if its balance factor is - 1,  0, or 1

A node is said to be left-heavy if its balance factor is -1

A node is said to be right-heavy if its balance factor is +1

LL rotation (left-heavy left-heavy rotation)

RR rotation (right-heavy right-heavy rotation)

LR rotation (left-heavy right-heavy rotation)

RL rotation (right-heavy left-heavy rotation)

design the AVL Tree class

AnAVL isa binary search tree, so we can define the AVLTreeclass to extend the BSTclass

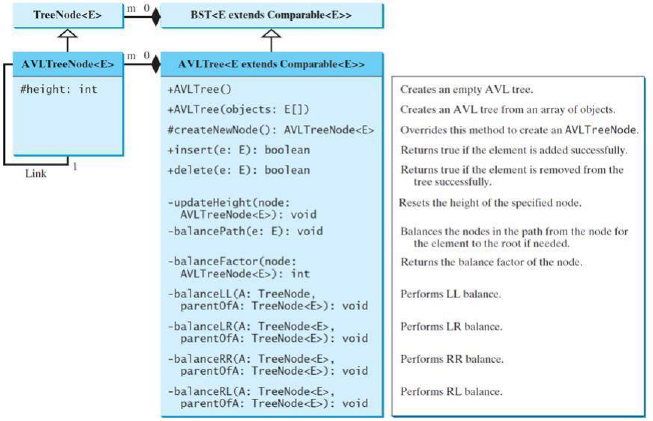
W12 Hashing

  To understand what hashing is and what hashing is used for
  To obtain the hash code for an object and design the hash function to map a key to an index
  To handle collisions using open addressing
  To know the differences among linear probing, quadratic probing, and double hashing
  To handle collisions using separate chaining
  To understand the load factor and the need for rehashing
  To implement MyHashMapusing hashing

Why hashing

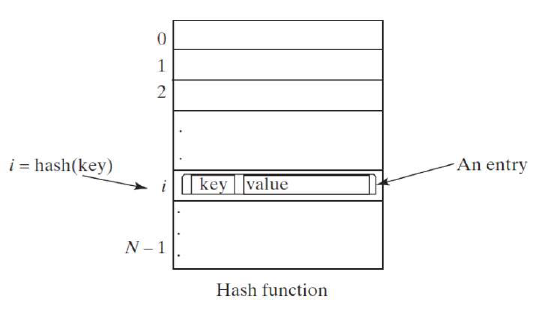
A map (dictionary, hash table, or associative array) is a data structure that stores entries, where each entry contains two parts: key (also called a search key) and value

O(1) time to search, insert, and delete an element in a set or amap vs. O(log n) time in a well-balanced search tree

implementation

To implement a map, can we store the values in an array and use the key as the index to find/set the value?
The answer is yes if you can map the key to an index

the array that stores the values is called a hash table

The function that maps a key to an index in the hash table is  called a hash function

Hashing is the technique that puts and retrieves the value using the index obtained from key in/from the hash table

Hash Function and hash codes

A typical hash function first converts a search key to an integer value called a hash code, then compresses the hash code into an index to the hash table

(Java’s root class Objecthas a hashCodemethod, which returns an integer hash
code -- by default, the method returns the memory address for the object (this is the decimal value of what toStringprints in hex))

You should override the hashCode method whenever the  equals method is overridden to ensure that two equal objects return the same hash code

Two unequal objects may have the same hash code (called a collision)

Hash Codes for Primitive Types

具体的看PPT哈

The types byte, short, char and int are simply casted into int

float  → int hashCode = Float.floatToIntBits(value);

long  →  int hashCode = (int)(value^(value>>32));

double → long bits = Double.doubleToLongBits(value);

                int hashCode = (int)(bits ^ (bits >> 32));

String → int hashCode = 0; 
                for (int i = 0; i < length; i++) 
                { hashCode = 31 * hashCode + charAt(i); }

Compressing Hash Codes

The hash code for a key can be a large integer that is out  of the range for the hash-table index 当一个键的hash code大于hash table index怎么办呢？

Assume the index for a hash table is between 0 and N-1 -- the most common way to scale an integer is h(hashCode)=hashCode % N

N is the number of buckets in a hash table, crucial for determining the index range in which entries are placed into. It can be fixed or variable, depending on the design and requirements of the hash table.

Handling Collisions

A hashing collision (or collision) occurs when two different keys are mapped to the same index in a hash table

There are two ways for handling collisions: open addressing and separate chaining

Open addressing

the process of finding an open location in the hash table in the event of a collision

Open addressing has several variations: linear probing, quadratic probing and double hashing

Linear probing

When a collision occurs during the insertion of an entry to a hash table, linear probing finds the next available location sequentially
If a collision occurs at hashTable[key % N], check whether hashTable[(key+1) % N]is available,If not, check hashTable[(key+2) % N]and soon,  until an available cell is found

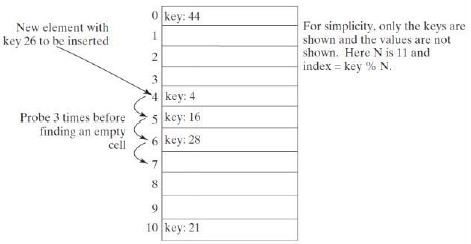
1) To remove an entry from the hash table, search the entry that matches the key,If the entry is found, place a special marker marked to denote that the entry is deleted, but available for insertion of other values

Each cell in the hash table has three possible states: occupied, marked, or empty ,a marked cell is also available for insertion

2) Linear probing tends to cause groups of consecutive cells in the hash table to be occupied -- each group is called a cluster

Each cluster is actually a probe sequence that you must search when retrieving, adding, or removing an entry

Disadvantage： As clusters grow in size, they may merge into even larger clusters, further slowing down the search time

Quadratic probing

Quadratic probing looks at the cells at indices (key+j^2)%N for j>=0, that is, key%N,  (key+1)%N,  (key+4)%N,     (key+9)%N, (key+16)%N, and soon

\

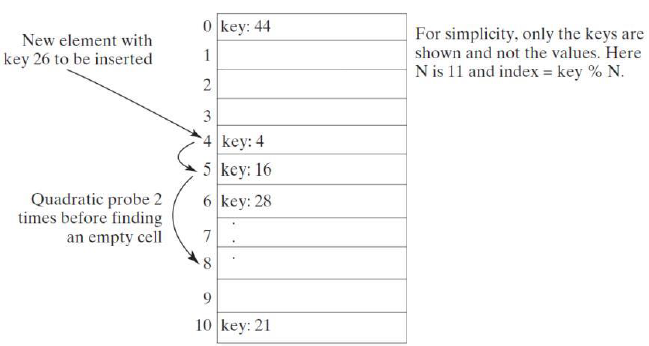works in the same way as linear probing for retrieval, insertion and deletion, except for the change in the search sequence

Quadratic probing can avoid the clustering problem in linear probing for consecutive keys

It still has its own clustering problem, called secondary  clustering for keys that collide with the occupied entry using the same probe sequence

Linear probing guarantees that an available cell can be found for insertion as long as the table is not full, there is no such guarantee for quadratic probing (it can have a cycle that skips the same positions)

double hasing

详情请看ppt

1. 第一次哈希：用第一个哈希函数 h1(key) 计算初始索引。
2. 第二次哈希：用第二个哈希函数 h2(key) 计算步长。

如果第一次哈希产生的索引已经被占用，就使用步长 h2(key) 来计算新的索引：(h1(key) + i * h2(key)) % N，其中 i 是尝试次数，N 是哈希表的大小。

双重散列确保每个键有独特的探测序列，从而减少冲突，提高哈希表的性能。

Separate chaining

The separate chaining scheme places all entries with the same hash index into the same location, rather than finding new locations

places all entries with the same hash index into the same location in a list

Each location in the separate chaining scheme is called a bucket

A bucket is a container that holds multiple entries:

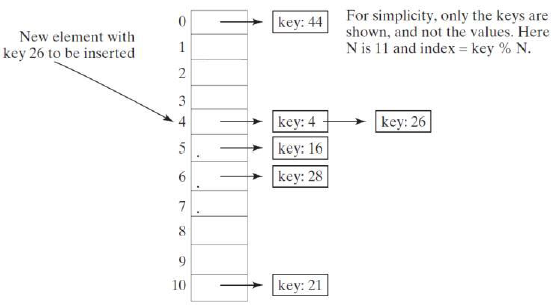
Collision in java.util.HashMapis possible because hash function uses hashCode() of key object which doesn't guarantee different hash codes for different objects.

<JDK8 : Linked list 

>JDK8 : balanced tree

Load Factor 

Load factor λ (lambda) is the ratio of the number of elements to the size of the hash table

λ =n/N
where n denotes the number of elements and N the number of locations in the hash table

For the open addressing scheme, λ is between 0 and 1

If the hash table is empty, then λ =0 If the hash table is full, then λ =1

For the separate chaining scheme, λ can be any value

Rehashing

As λ increases, the probability of a collision increases

Because the load factor measures how full a hash table is

You should maintain the load factor under 0.5for the open addressing schemes and under 0.9for the separate chaining scheme(In the implementation of the java.util.HashMap class in the Java API, the threshold 0.75is used)

If the load factor is exceeded, we increase the hash-table size and reload the entries into a new larger hash table -> this is called rehashing

We need to change the hash functions, since the hash-table size has been  changed, To reduce the likelihood of rehashing, since it is costly, you should at least  double the hash-table size