[CUDA 学习笔记] 稀疏矩阵向量乘法(SpMV) CUDA 实现与优化

稀疏矩阵向量乘法(SpMV) CUDA 实现与优化

本文主要围绕基于 CUDA 的 SpMV 实现进行介绍, 包括几种典型稀疏矩阵存储格式下 SpMV 的朴素实现, 以及 CSR 格式下的几种优化实现.

稀疏矩阵存储格式

稀疏矩阵即含有大量零元的矩阵. 对于稀疏矩阵, 像稠密矩阵一样使用二维数组来存储数据会浪费大量内存空间, 一般采用特殊的数据结构来存储非零元, 以减少内存使用并尽可能有较高的访问效率.

比较典型的稀疏矩阵存储格式有: CSR(Compressed Sparse Row), CSC(Compressed Sparse Column), COO (Coordinate), ELL(ELLPACK), BSR(Block Sparse Row), HYB (hybrid) 等等. 不同的存储格式有着不同的数据压缩特点, 对于不同稀疏矩阵数据以及不同的数据访问模式有着不同的性能效果, 各具优劣.
关于稀疏矩阵的存储格式, 可以参考文章: 稀疏矩阵存储格式总结+存储效率对比:COO,CSR,DIA,ELL,HYB - Bin的专栏 - 博客园 以及 NVIDIA cuSparse 文档中稀疏矩阵存储格式的介绍, 在此不多赘述.

SpMV cuSparse 函数

在 NVIDIA cuSparse 库中, 提供了针对 SpMV 的一组 API, 包括 cusparseSpMV_bufferSize() 和 cusparseSpMV() 两个函数. 关于函数的接口参数、支持的稀疏矩阵格式与数据类型等具体信息, 可以参考其文档. 在此不多赘述.
在 GitHub 仓库 NVIDIA/CUDALibrarySamples 中, 给出了 CSR 和 COO 格式使用 SpMV API 的代码示例: SpMV_csr_example.c, SpMV_coo_example.c.

SpMV CUDA 朴素实现

标准的稀疏矩阵向量乘法(Sparse Matrix-Vector Multiplication)执行以下操作:
Y = α A ⋅ X + β Y \textbf{Y}=\alpha\textbf{A}\cdot\textbf{X}+\beta\textbf{Y} Y=αA⋅X+βY
其中, A \textbf{A} A 为大小 m × k m\times k m×k 的稀疏矩阵, X \textbf{X} X 是长度为 k k k 的稠密向量, Y \textbf{Y} Y 是长度为 m m m 的稠密向量, α \alpha α 和 β \beta β 是标量.
在很多时候, SpMV 主要是针对 α = β = 1 \alpha=\beta=1 α=β=1, Y = 0 ⃗ \textbf{Y}=\vec{\textbf{0}} Y=0 的情况, 即围绕核心的"稀疏矩阵向量乘"的部分 A ⋅ X \textbf{A}\cdot\textbf{X} A⋅X 进行讨论, 后文有关 SpMV 的实现也主要针对该特殊情况下的实现.

很显然, 对于不同的稀疏矩阵存储格式, 其 SpMV 的实现会有一些不同. 接下来主要给出了 Sparse Matrix-Vector Multiplication with CUDA | by Georgii Evtushenko | Analytics Vidhya | Medium 文章中提到的几种经典稀疏矩阵存储格式下 SpMV 的 CUDA 朴素实现(所谓朴素实现, 即基本上未使用任何优化方法的实现).

CSR SpMV (CSR-Scalar 与 CSR-Vector)

CSR-Scalar SpMV 的 kernel 代码如下:

template <typename data_type>
__global__ void csr_SpMV_kernel (unsigned int n_rows,const unsigned int *col_ids,const unsigned int *row_ptr,const data_type *data,const data_type*x，data_type *y) {unsigned int row = blockIdx.x * blockDim.x + threadIdx.x ;if (row < n_rows) {const int row_start = row_ptr[row];const int row_end = row_ptr[row + 1];data_type sum = 0;for (unsigned int element = row_start; element < row_end; element++) {sum += data[element] * x[col_ids[element]];}y[row] = sum;}
}

代码逻辑很简单, 简而言之就是让 CUDA 的每个线程负责 CSR 矩阵每一行的计算. 由于矩阵每行乘以向量的计算结果是一个标量, 因此被称之为 “CSR-Scalar SpMV”.

CSR-Vector SpMV 的 kernel 代码如下:

template <typename data_type>
__global__ void csr_SpMV_vector_kernel (unsigned int n_rows,const unsigned int *col_ids,const unsigned int *row_ptr,const data_type *data,const data_type *x,data_type *y) {const unsigned int thread_id = blockIdx.x * blockDim.x + threadIdx.x;const unsigned int warp_id = thread_id / 32;const unsigned int lane = thread_id % 32;const unsigned int row = warp_id;    //< One warp per rowdata_type sum = 0;if (row < n_rows) {const unsigned int row_start = row_ptr[row];const unsigned int row_end = row_ptr[row + 1];for (unsigned int element = row_start + lane; element < row_end; element += 32) {sum += data[element] * x[col_ids[element]];}}sum = warp_reduce (sum);if (lane == 0 && row < n_rows) {y[row] = sum;}
}template <class T>
__device__ T warp_reduce (T val) {for (int offset = warpSize / 2; offset > 0; offset /= 2) {val += __shfl_down_sync(FULL_WARP_MASK, val, offset);}return val;
}

CSR-Vector SpMV 则是让每个 warp 负责 CSR 矩阵每一行的计算, 由于 warp 中有 32 个线程, 因此计算结束后每行是一个 32 维的向量, 需要通过 warp 内的归约操作 warp_reduce() 得到最终的结果, 并由 lane 0 线程写回结果向量.

容易分析得到, CSR-Scalar 与 CSR-Vector 两种 SpMV 在线程的负载均衡上会有较大问题, 这也是 SpMV 这一计算在 CUDA 上实现所面临的一个主要问题. 由于稀疏矩阵的特性, 矩阵的每一行非零元个数会各有不同, 尤其是对一些幂律性比较突出的稀疏矩阵, 行中的非零元可能差别很大, 因此, 在 CSR-Scalar 中不同线程之间的工作量可能会相乘很大, 从而导致 warp divergence 等问题, 大幅影响性能; CSR-Vector 将一个 warp 负责矩阵的一行, 一定程度上减轻了 warp 内线程的负载不均与 warp divergence, 但有时矩阵行中的非零元较少, 32 个线程就会存在线程空闲的问题, 同时 warp 间的负载不均依旧存在.

ELL SpMV

ELL 格式稀疏矩阵的 SpMV 朴素实现 kernel 代码如下:

template <typename data_type>
__global__ void ell_SpMV_kernel (unsigned int n_rows,unsigned int elements_in_rows,const unsigned int *col_ids,const data_type *data,const data_type *x,data_type *y) {unsigned int row = blockIdx.x * blockDim.x + threadIdx.x;if (row < n_rows) {data_type sum = 0;for (unsigned int element = 0; element < elements_in_rows; element++) {const unsigned int element_offset = row + element * n_rows;sum += data[element_offset] * x[col_ids[element_offset]];}y[row] = sum;}
}

ELL 格式稀疏矩阵同样是将矩阵在行方向上进行压缩, 不过会通过填充占位元素让矩阵仍然保持行中元素相同. 上面的代码采用的 0 填充, 因此在计算是填充元素可以和非零元一样计算而不会影响结果.
与 CSR-Scalar 类似, 这里也是采取的每个线程负责 ELL 矩阵的一行. 由于 ELL 格式保证了行方向元素数是相同的且内存排布一致, 因此相比与 CSR-Scalar, 此处线程负载不均和 warp divergence 的问题会小很多; 但同样正是由于填充的占位元素, 会产生大量无用的计算影响性能.

COO SpMV

COO 格式稀疏矩阵的 SpMV 朴素实现 kernel 代码如下:

template <typename data_type>
__global__ void coo_SpMV_kernel (unsigned int n_elements,const unsigned int *col_ids,const unsigned int *row_ids,const data_type *data,const data_type *x,data_type *y) {unsigned int element = blockIdx.x * blockDim.x + threadIdx.x;if (element < n_elements) {atomicAdd(y + row_ids[element], data[element] * x[col_ids[element]]);}
}

COO 矩阵格式的 SpMV 代码更加简单, 即让每个线程负责矩阵中的一个非零元的计算. 由于 COO 格式下非零元是以三元组的形式存储, 因此写回结果到结果向量时需要使用原子操作 atomicAdd() 保证数据一致性.
相比与前面矩阵格式的 SpMV, COO 在线程负载上比较均衡, 但原子操作严重影响了更新结果的性能.

HYB SpMV

HYB 格式稀疏矩阵的 SpMV 朴素实现 kernel 代码如下:

template <typename data_type>
__global__ void hybrid_SpMV_kernel (unsigned int n_rows,unsigned int n_elements,unsigned int elements_in_rows,const unsigned int *ell_col_ids,const unsigned int *col_ids,const unsigned int *row _ids,const data_type *ell_data,const data_type *coo_data,const data_type *x,data_type *y) {const unsigned int idx = blockIdx.x * blockDim.x + threadIdx.x;if (idx < n_rows) {const unsigned int row = idx;data_type sum = 0;for (unsigned int element = 0; element < elements_in_rows; element++) {const unsigned int element_offset = row + element * n_rows;sum += ell_data[element_offset] * x[ell_col_ids[element_offset]];}atomicAdd(y + row，sum);}for (unsigned int element = idx; element < n_elements; element += blockDim.x * gridDim.x) {const data_type sum = coo_data[element] * x[col_ids[element]];atomicAdd(y + row _ids[element], sum);}
}

HYB 格式是 ELL+COO 两种格式的混合, 核心思想是将非零元过多的行的多出来的元素由 COO 格式存取, 从而让 ELL 格式中不会添加过多的填充元素.
在 SpMV 实现上, 也是将两种 SpMV 方式进行了结合. 不同之处在于, 由于现在矩阵一行的元素可能分别在 ELL 和 COO 格式中存储, 因此更新结果向量时都要使用原子操作.

BSR SpMV

BSR(Block Sparse Row), 有的文章中也称之为 BCSR(Block Compressed Sparse Row), 考虑到 Bitmap Compressed Sparse Row 格式也被称之为 BCSR, 所以笔者习惯沿用 NVIDIA 文档中 BSR 的叫法.
BSR 与 CSR 类似, 只不过其粒度不再是 CSR 中的单个非零元, 而是一个非零元分块, 具体可以参考 NVIDIA BSR 部分的文档.

BSR 格式矩阵的 SpMV 朴素实现, 笔者这里参考了文章 使用CUDA实现块稀疏矩阵向量乘（BSpMV） - 知乎 以及论文 Optimization of block sparse matrix-vector multiplication on shared-memory parallel architectures.
在文中, 主要提到了两种计算方法:

  1. Block row per warp, operating by block. 即每个 warp 负责处理 BSR 一行的分块; 而一个 warp 一次迭代中负责该行中整数个( ⌊ W A R P _ S I Z E / ( b l o c k _ s i z e × b l o c k _ s i z e ) ⌋ \lfloor WARP\_SIZE/(block\_size\times block\_size)\rfloor ⌊WARP_SIZE/(block_size×block_size)⌋)分块, 换句话说就是 warp 的线程 2D 平铺在该行的每个矩阵分块上.
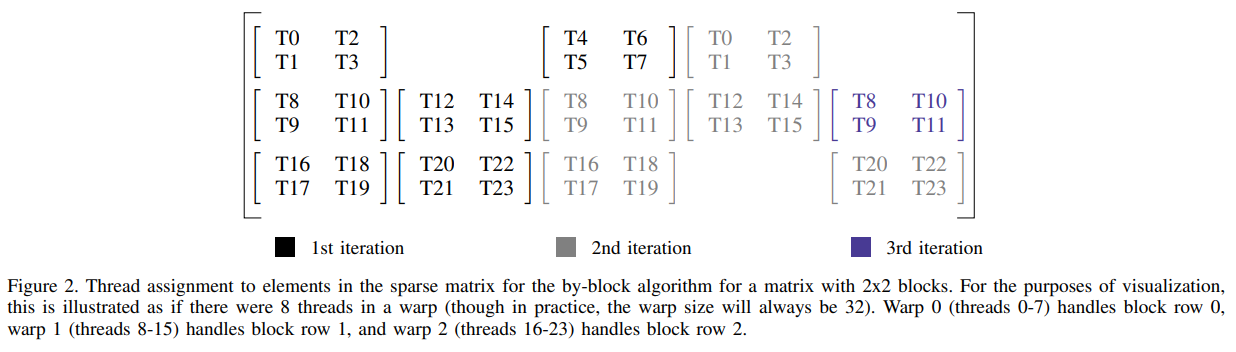
    在这里插入图片描述
  2. Block row per warp, operating by column. 即每个 warp 仍然负责处理 BSR 一行的分块; 但一个 warp 一次迭代负责该行的整数个( ⌊ W A R P _ S I Z E / b l o c k _ s i z e ⌋ \lfloor WARP\_SIZE/block\_size\rfloor ⌊WARP_SIZE/block_size⌋)列, 换句话说就是 warp 的线程按列平铺在该行的每个矩阵分块上.
    在这里插入图片描述
    这个图有点问题, 根据图的标题可以看出, 前两行 T27~T29 以及 T59~T61 应该是深黑色的, 其在 warp 第一次迭代时就可计算.

关于具体实现的伪代码和 CUDA 代码可以参考上面的博客以及论文, 在此不多赘述.

CSR 格式 SpMV CUDA 优化实现

SpMV 在 memory bound 和 compute bound 角度来看, 很显然是一个 memory bound 的问题. 稀疏矩阵带来的访存不规则会导致难以合并读写、缓存命中率低、数据难以重用等问题, 以及有时需要原子操作等, 都会使得访存效率低下. 而对于像 CSR 等格式, 压缩存储也会导致 SpMV 计算时负载不均、warp divergence 的问题, 进而导致 GPU 利用率不高.
到目前为止也有很多关于 SpMV 优化的工作, 由于 SpMV 访存效率的低下, 很多工作就是围绕访存进行优化. 很常见的一种思路就是结合稀疏矩阵的存储格式和算法, 来优化计算过程中的访存, 因此很多工作会涉及一些独特的稀疏矩阵存储格式, 以及格式转换、数据分块、对齐填充等方面的预处理工作, 以便在实际的 SpMV 计算时提高访存效率. 此外, 也有一些工作会结合多种矩阵格式的优点, 根据矩阵稀疏特性进行格式选择, 并选择相应的算法, 以提高计算性能.
相关工作可以参考 稀疏矩阵格式调研 - 杜臻 - 博客园 和 SpMV矩阵格式自动调优 - 杜臻 - 博客园 两篇文章, 文章作者介绍了很多近年 SpMV 方面的研究工作.

在这里, 笔者主要关注于 GPU 上 CSR 矩阵格式的 SpMV 优化. 关注 CSR 矩阵格式的工作, 主要因为这是在计算中最为经典和常用的稀疏矩阵存储格式之一, 因此相关的优化实现可以相对方便的集成到所需之处; 而很多工作使用的稀疏矩阵格式要么不够常见, 要么是自己提出的, 要么是多格式混合的, 总之往往需要复杂的预处理工作, 数据结构的转换导致实际集成使用相对困难.
下面笔者主要介绍几个代码开源的 GPU 上 CSR 矩阵的 SpMV 工作.

CUSP CSR-Vector

CUSP 是一个开源的稀疏矩阵库, 其中给出了一种 CSR-Vector 的实现方式.
与上文提到的 CSR-Vector 的朴素实现不同的是, CUSP 由 warp 中连续的 THREADS_PER_VECTOR 个线程处理 CSR 矩阵的一行; 相当于对一个 warp 的线程进行了分组, 每个 warp 可以同时负责矩阵多行的计算.
由于 CUSP 是一个比较早的 CUDA 实现, 其 warp 内归约仍使用的共享内存, 这里笔者还参考了文章 深入浅出GPU优化系列：spmv优化 - 知乎 中的实现, 结合了 warp shuffle 指令来提高归约效率.

template <unsigned VECTORS_PER_BLOCK, unsigned THREADS_PER_VECTOR,typename index_t, typename offset_t, typename mat_value_t,typename vec_x_value_t, typename vec_y_value_t,typename unary_func_t, typename binary_func1_t, typename binary_func2_t>
__global__ void 
cusp_warp_read_reduce_kernel(index_t n_rows, const offset_t *Ap, const index_t *Aj, const mat_value_t *Ax, const vec_x_value_t *x, vec_y_value_t *y,unary_func_t initialize, binary_func1_t combine, binary_func2_t reduce) {constexpr offset_t THREADS_PER_BLOCK = VECTORS_PER_BLOCK * THREADS_PER_VECTOR;const offset_t thread_id   = THREADS_PER_BLOCK * blockIdx.x + threadIdx.x;    // global thread indexconst offset_t thread_lane = threadIdx.x & (THREADS_PER_VECTOR - 1);          // thread index within the vectorconst offset_t row_id   = thread_id   /  THREADS_PER_VECTOR;               // global vector indexif (row_id < n_rows) {        offset_t row_start = Ap[row_id];offset_t row_end = Ap[row_id + 1];// initialize local sumvec_y_value_t sum = (thread_lane == 0) ? initialize(y[row_id]) : vec_y_value_t(0);if (THREADS_PER_VECTOR == 32 && row_end - row_start > 32) {// ensure aligned memory access to Aj and Axoffset_t jj = row_start - (row_start & (THREADS_PER_VECTOR - 1)) + thread_lane;// accumulate local sumsif(jj >= row_start && jj < row_end)sum = reduce(sum, combine(Ax[jj], x[Aj[jj]]));// accumulate local sumsfor(jj += THREADS_PER_VECTOR; jj < row_end; jj += THREADS_PER_VECTOR)sum = reduce(sum, combine(Ax[jj], x[Aj[jj]]));} else {// accumulate local sumsfor(offset_t jj = row_start + thread_lane; jj < row_end; jj += THREADS_PER_VECTOR)sum = reduce(sum, combine(Ax[jj], x[Aj[jj]]));}// reduce local sums to row sumsum = WarpReduce<THREADS_PER_VECTOR>(sum, reduce);// first thread writes the resultif (thread_lane == 0) {y[row_id] = sum;}}
}template <unsigned size, typename T, typename binary_func_t>
__device__ __forceinline__
T WarpReduce(T sum, binary_func_t reduce) {if constexpr (size >= 32) sum = reduce(sum, __shfl_down_sync(FULL_MASK, sum, 16)); // 0-16, 1-17, 2-18, etc.if constexpr (size >= 16) sum = reduce(sum, __shfl_down_sync(FULL_MASK, sum, 8));  // 0-8, 1-9, 2-10, etc.if constexpr (size >= 8)  sum = reduce(sum, __shfl_down_sync(FULL_MASK, sum, 4));  // 0-4, 1-5, 2-6, etc.if constexpr (size >= 4)  sum = reduce(sum, __shfl_down_sync(FULL_MASK, sum, 2));  // 0-2, 1-3, 4-6, 5-7, etc.if constexpr (size >= 2)  sum = reduce(sum, __shfl_down_sync(FULL_MASK, sum, 1));  // 0-1, 2-3, 4-5, etc.return sum;   
}

上述代码中, 由三个部分需要说明:

  • 在 THREADS_PER_VECTOR == 32 && row_end - row_start > 32 时, 即整个 warp 计算矩阵一行且针对矩阵该行元素过多的情况, CUSP 进行了地址对齐的读取, 以提高 warp 的读取效率. 不过一般情况下, THREADS_PER_VECTOR 的值小于 32.
  • 关于 warp 内的归约, CUSP 的两种实现中要么使用共享内存, 要么使用 CUB 库提供的 WrapReduce 算法. 在这里笔者使用了基于 shuffle 指令的 warp 归约方法.
  • 在 CUSP 原本代码中, 使用了共享内存配合每个分组的前两个线程来读取矩阵的每行的起始偏移和终止偏移. 然后该分组的每个线程再从共享内存中读取这两个值. 即利用共享内存减少对全局内存的访问.
    __shared__ volatile offset_t ptrs[VECTORS_PER_BLOCK][2];
if(thread_lane < 2)ptrs[vector_lane][thread_lane] = Ap[row + thread_lane];const offset_t row_start = ptrs[vector_lane][0];                   //same as: row_start = Ap[row];
const offset_t row_end   = ptrs[vector_lane][1];                   //same as: row_end   = Ap[row+1];
    同样的, 这里在算力 7.0 以上设备应该在 if 语句后加 __syncwarp() 进行 warp 同步. 或者使用如下基于 shuffle 指令的代码达到相同效果. 不过在实际性能测试中发现, 即使这里直接让每个线程从全局内存直接读取行偏移, 性能也不会产生太大影响, 甚至性能还会好一点.
    offset_t row_offsets[2];
if (thread_lane < 2) {row_offsets[thread_lane] = Ap[row_id + thread_lane];
}offset_t row_start = __shfl_sync(FULL_MASK, row_offsets[0], row_id * THREADS_PER_VECTOR);
offset_t row_end = __shfl_sync(FULL_MASK, row_offsets[1], row_id * THREADS_PER_VECTOR + 1);
  • 在模板参数 THREADS_PER_VECTOR 的选择上, CUSP 是基于稀疏矩阵的结点平均度数 nnz/n_rows 确定的, 并要求其一定是 2 的幂次.
    const offset_t nnz_per_row = nnz / n_rows;if (nnz_per_row <=  2) {__cusp_csr_vector<2>(n_rows, Ap, Aj, Ax, x, y, initialize, combine, reduce);return;
}
if (nnz_per_row <=  4) {__cusp_csr_vector<4>(n_rows, Ap, Aj, Ax, x, y, initialize, combine, reduce);
}
// ...

LightSpMV

LightSpMV 是 ASAP’15 上发表的论文 “LightSpMV: Faster CSR-based sparse matrix-vector multiplication on CUDA-enabled GPUs” 的实现. 不过这个实现基本上没有太大参考价值.
其关键部分与 CUSP CSR-Vector 的实现基本一致. 区别主要在于其使用一个行计数变量 cudaRowCounters 以及原子操作 AtomicAdd() 来让线程或 warp 去拿取需要处理的矩阵行号, 而不是像 CUSP CSR-Vector 直接根据线程 ID 计算得到.
论文中, 有 vector-level 和 wrap-level 两种实现, 前者即每个线程分组的 0 号线程使用原子操作拿取 1 行; 后者是 1 个 warp 的 0 号线程使用原子操作拿取 32 / THREADS_PER_VECTOR 行, 然后 warp 内的每个线程分组在计算出对应行号.

if (laneId == 0) {row = atomicAdd(cudaRowCounter, 1);
}
/*broadcast the value to other lanes from lane 0*/
row = shfl(row, 0, THREADS_PER_VECTOR);

// Warp-Level
if (warpLaneId == 0) {row = atomicAdd(cudaRowCounter, 32 / THREADS_PER_VECTOR);
}
row = shfl(row, 0) + warpVectorId;

此外, 在实现中, 其利用 cudaTextureObject_t 等接口, 将向量 X 绑定到 CUDA 的纹理内存(Texture Memory). 不过在实际测试中发现, 使用纹理内存对性能提升是负作用.
在实际测试时, 该实现方法并不如 CUSP 的 CSR-Vector 实现, 推断原子操作在执行时实际上也是串行的, 并不如直接通过 row_id = thread_id / THREADS_PER_VECTOR 计算得到的并行性好.

Merge-based SpMV

Merge-based SpMV 是 SC’16 上发表的论文 “Merge-Based Parallel Sparse Matrix-Vector Multiplication” 的实现, 现合并到了 CUB 库中, GitHub 中也有其开源实现, 不过版本有些过时.

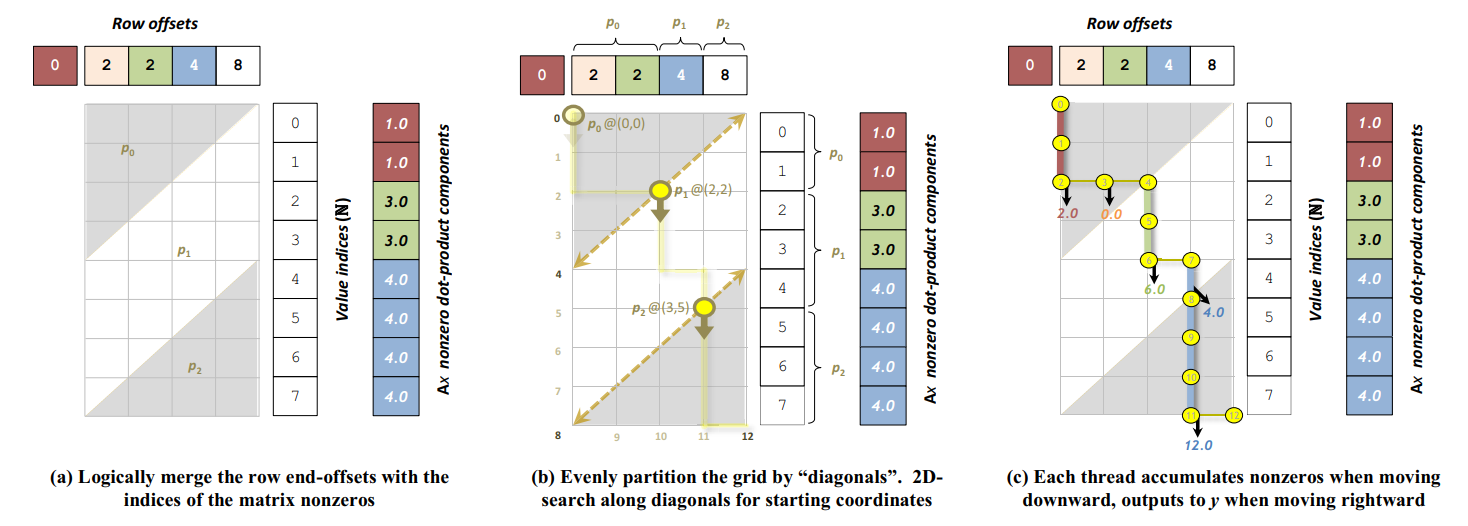
该实现的核心是将 SpMV 转化为 CSR 行偏移数组和 CSR 非零元序列的路径合并问题.
如下图所示, 对于坐标 ( x , y ) (x,y) (x,y), x ∈ R o w O f f s e t s x\in RowOffsets x∈RowOffsets, y ∈ V a l u e I n d i c e s = [ 0 , n n z ] y\in ValueIndices=[0,nnz] y∈ValueIndices=[0,nnz], 当 R o w O f f s e t s [ x ] > V a l u e I n d i c e s [ y ] RowOffsets[x]>ValueIndices[y] RowOffsets[x]>ValueIndices[y] 时, 路径向下移动, 并进行非零元计算; 反之, 路径向右移动.
在并行实现上, 每个线程负责相同长度的合并路径(行索引+非零元)进行路径合并. 在路径合并前, 每个线程需要通过对角线的二分搜索确定搜索的起始坐标, 具体而言是沿对角线 k k k 找到第一个 ( i , j ) (i,j) (i,j), 其 A i A_i Ai​ 大于所有 B j B_j Bj​ 之前的元素 , 其中 i + j = k i+j=k i+j=k.
通过这种路径合并的思路, GPU 的不同线程块以及线程块的不同线程之间, 能够处理数量解决的元素(行偏移或非零元), 从而达到较好的负载均衡. 同时, 不同线程之间通过二分搜索确定起始坐标, 没有相互依赖, 可以很大程度上并行. 但额外的, 该算法需要单独处理跨线程/线程块的行的计算结果的合并问题.
外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传
在具体实现方面, 由于代码比较复杂, 且考虑了不同算力的设备, 在此主要介绍代码的主要计算流程.
代码对外接口函数为 cub::DeviceSpmv::CsrMV(), 其内部主要由 4 个 kernel 函数组成, 除去用于处理矩阵仅有 1 列的特殊情况的 kernel DeviceSpmv1ColKernel (为 CSR-Scalar 实现) 外, 主要由 DeviceSpmvSearchKernel DeviceSpmvKernel 以及 DeviceSegmentFixupKernel 三个 kernel 组成.

  • DeviceSpmvSearchKernel: 通过调用 MergePathSearch() 函数使用二分搜索来确定每个线程块负责的线程块级别合并路径分片的起始坐标, 并存入临时内存中. 当线程块数目较少时, 该 kernel 不会被调用, 线程块起始的确定会移至后续的 DeviceSpmvKernel 中.
  • DeviceSpmvKernel: 进行核心的 SpMV 计算, 即合并路径.
    1. 首先会判断是否通过 DeviceSpmvSearchKernel 计算了线程块合并路径的起始坐标, 否则则先使用 2 个线程分别计算线程块合并路径的起始坐标和终止坐标.
    2. 进行线程级别的路径合并. 在这里根据是否将非零元向量乘的中间结果暂存到共享内存中, 对应两个 AgentSpmv::ConsumeTile() 的实现. 在此主要介绍使用共享内存的情况.
      每个线程会先计算 ITEMS_PER_THREAD 个非零元与对应向量 X 中元素的点积结果, 并写入共享内存中.
      然后进行每个线程进行线程级别分片的合并路径. 每个线程会计算自己负责的分片的起始坐标, 并进行上图所示的路径合并.
    3. 会通过 BlockScan::ExclusiveScan() 进行线程块级别的非包含前缀和的计算, 从而合并跨线程分片的矩阵行的点积结果. 每一行的结果都会写入共享内存中, 之后会统一写回全局内存的向量 Y 中. 最后返回线程块级别的归约结果 tile_carry, 用于后续合并跨线程块分片的矩阵行的点积结果.
  • DeviceSegmentFixupKernel: 处理跨线程块分片的矩阵行的点积结果的合并. 在具体实现上, 会根据 CSR 非零元的数据类型选择使用原子操作还是线程块归约, ,来完成结果的合并, 分别对应两个 AgentSegmentFixup::ConsumeTile() 实现.
    对于前者, 即直接使用原子操作 AtomicAdd(), 将不同线程块计算的同一矩阵行的部分点积结果直接加到向量 Y 上. 而对于后者, 则采取和处理跨线程分片的矩阵行一样的操作, 即使用 BlockScan::ExclusiveScan() 合并同一行的点积结果后再一次性写入向量 Y 中. 对于 AtomicAdd() 支持的 int unsigned float 等数据类型, 会默认使用前者, 而后者则是一个更为通用的方式. 而在性能上, 二者的差别并不是特别明显.

性能测试

笔者从 SuiteSparse Matrix Collection 中选择了以下 8 个稀疏程度各异的数据集进行了以上几种实现的性能测试.
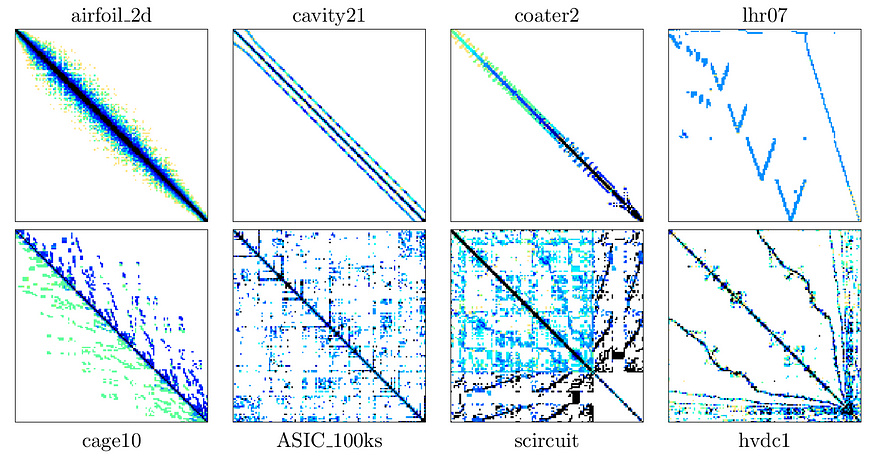
在这里插入图片描述
数据集的基本信息和稀疏程度如下表所示:

datasetn_rowsn_colsnnz稀疏度
nnz/(n_row * n_cols)
airfoil_2d14214142142596880.001285
ASIC_100ks99190991905788900.000059
cage1011397113971506450.00116
cavity21456245621381870.00664
coater2954095402073080.002278
hvdc124842248421599810.000259
lhr07733773371565080.002907
scircuit1709981709989589360.000033

在 SpMV 实现上, 笔者选择了 NVIDIA HPC 库中 cuSparse 的 CSR 格式的 SpMV 实现以及上文提到的几种 CSR 格式的 SpMV 实现, 包括: CUSP 的 CSR-Vector 实现; LightSpMV 的 vector-level 与 warp-level 的实现; 以及 NVIDIA CUB 库中 Merge-based SpMV 的实现.

下图显示了这几种 SpMV 实现在 8 个数据下的性能情况, 其中纵轴表示的是该实现核心 kernel 部分的执行耗时 (核心 API 及 kernel 的执行耗时, 不包括辅助临时内存申请等耗时):
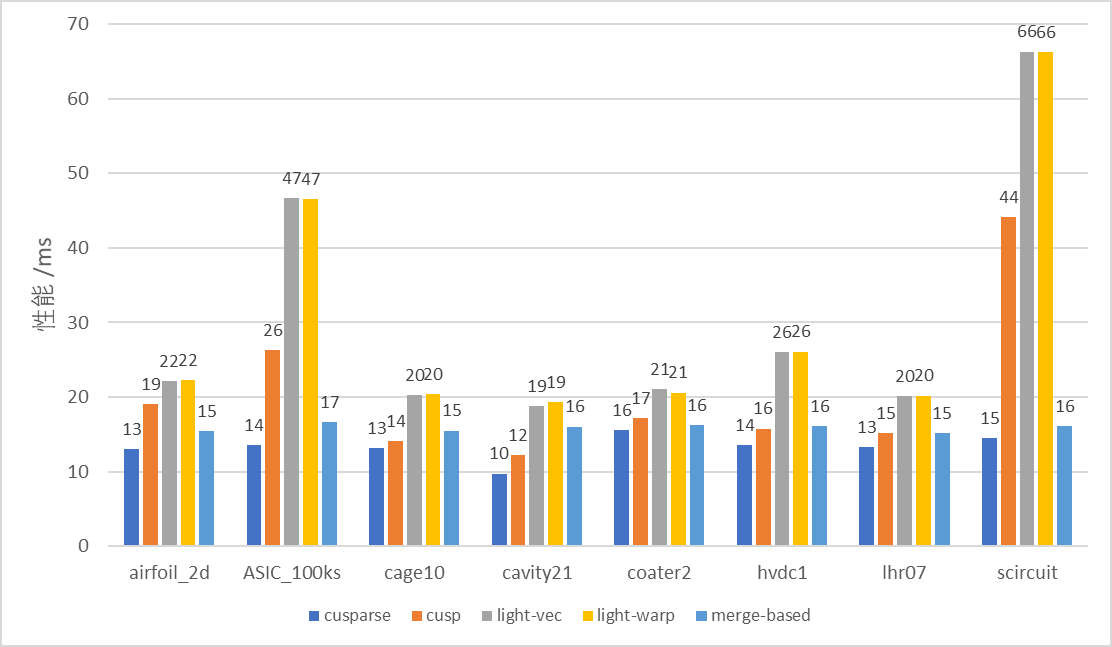
在这里插入图片描述
下表展示了上面几种 SpMV 实现在如上 8 个数据下完整执行的耗时, 包括临时辅助内存的申请、纹理内存绑定等预处理操作:

cusparsecusplight-veclight-warpmerge-based
airfoil_2d295.6119.0245313.788313.679541.189
ASIC_100ks304.659526.591344.216342.6860.9195
cage10294.725514.0465313.609313.89840.7435
cavity21284.757512.592308.518314.844536.5605
coater2304.91517.5445324.9845315.854540.7175
hvdc1296.293516.044319.6345320.421541.6205
lhr07295.738515.4105315.046314.59939.671
scircuit333.53444.133369.182363.225598.1395

结合图表可以看出, 对于 SpMV 的核心 kernel 耗时, 在不同稀疏特性的数据集下, 英伟达官方的 cuSparse 库提供了相比其他方法最佳的执行性能, 但比较明显的是其总耗时比较高, 主要是其临时内存的申请占据了大量时间; 而 Merged-based 实现虽然比 cuSparse 的性能稍差, 但整体上在不同数据集上均发挥了比较好的性能, 而且其总耗时相对 CuSparse 明显更低, 应该是其临时内存申请的数量更少的缘故; CUSP 的 CSR-Vector 的性能大多数情况下不如前两者, 但在一些数据集上能达到和 Merge-based 相近甚至更好的性能水平, 猜测是一些行稀疏度均匀的情况, 而该方法的特点在于无需额外申请临时内存, 因此总时间开销与核心 kernel 实现开销基本一致, 在考虑临时内存的情况下, 该方法反而是总耗时最低的; LightSpMV 的两种方法在各个数据集上性能表现均为最差, 两种方法的性能差距不大, 此外由于使用了纹理内存来绑定向量, 其总耗时也很高, 不是一种好的实现.

额外一提的是, ICS’17 上有一篇 Hola-SpMV 的文章, 同样是 CSR 格式下的 SpMV 的 GPU 实现, 据文章描述, 该方法相比于 Merge-based 方法仍有性能提升, 并开源了源代码. 由于时间原因, 笔者并未对该方法进行学习研究和测试, 如有时间会考虑补充.

性能测试的代码在 GitHub 仓库 peakcrosser7/spmv-samples 中.

参考资料

  • 稀疏矩阵存储格式总结+存储效率对比:COO,CSR,DIA,ELL,HYB - Bin的专栏 - 博客园
  • cuSPARSE - NVIDIA Documentation Hub
  • Sparse Matrix-Vector Multiplication with CUDA | by Georgii Evtushenko | Analytics Vidhya | Medium
  • Eberhardt R, Hoemmen M. Optimization of block sparse matrix-vector multiplication on shared-memory parallel architectures[C]//2016 IEEE International Parallel and Distributed Processing Symposium Workshops (IPDPSW). IEEE, 2016: 663-672. https://ieeexplore.ieee.org/document/7529927
  • 稀疏矩阵格式调研 - 杜臻 - 博客园
  • SpMV矩阵格式自动调优 - 杜臻 - 博客园
  • CUSP : A C++ Templated Sparse Matrix Library. - GitHub
  • Liu Y, Schmidt B. LightSpMV: Faster CSR-based sparse matrix-vector multiplication on CUDA-enabled GPUs[C]//2015 IEEE 26th International Conference on Application-specific Systems, Architectures and Processors (ASAP). IEEE, 2015: 82-89. https://ieeexplore.ieee.org/document/7245713
  • Merrill D, Garland M. Merge-based parallel sparse matrix-vector multiplication[C]//SC’16: Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis. IEEE, 2016: 678-689. https://ieeexplore.ieee.org/document/7877136

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/348092.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

组织创新｜AI赋能敏捷实践，助力企业敏捷转型

组织创新｜AI赋能敏捷实践，助力企业敏捷转型

在工业5.0时代&#xff0c;随着项目变得越来越复杂&#xff0c;对效率的需求也在增长&#xff0c;致力于敏捷转型的组织正在寻求创新的解决方案来应对常见的挑战&#xff1a;工作量不平衡、低效的任务分配和知识孤岛等等。对此&#xff0c;AI等尖端技术的潜力可以帮助实现更高效…
阅读更多...
译译交友项目介绍

译译交友项目介绍

一、 项目背景 随着社会的进步&#xff0c;英语作为一种国际语言&#xff0c;很多人都在学习英语&#xff0c;然而现在很多人都会因为学习英语而烦恼&#xff0c;有时还会因为是一个人学习而感到枯燥。面对情绪的低落&#xff0c;往往会使学习更困难。因此&#xff0c;我打造了…
阅读更多...
电视剧推荐

电视剧推荐

1、《春色寄情人》 2、《唐朝诡事录》 3、《南来北往》 4、《与凤行》 5、《利剑玫瑰》 6、《承欢记》
阅读更多...
uniapp使用vue3语法构建自定义导航栏，适配小程序胶囊

uniapp使用vue3语法构建自定义导航栏，适配小程序胶囊

具体代码 <view v-if"isCustom" class"nav-content-container" :style"height:navContentHeight px;"><slot name"left"></slot><slot name"middle"> </slot><view :style"width:…
阅读更多...
网工内推 | 深信服、中软国际技术支持工程师，最高13k*13薪

网工内推 | 深信服、中软国际技术支持工程师，最高13k*13薪

01 深信服 &#x1f537;招聘岗位&#xff1a;远程技术支持工程师 &#x1f537;任职要求&#xff1a; 一、专业能力和行业经验&#xff1a; ①具备友商同岗位工作经验1.5年以上&#xff0c;具备良好的分析和判断能力&#xff0c;有独立问题处理思路&#xff0c;具备常见协…
阅读更多...
SpringAI调用OpenAI Demo

SpringAI调用OpenAI Demo

Spring AI 在maven的setting.xml <mirror> <id>spring-milestones</id> <name>Spring Milestones</name> <mirrorOf>spring-milestones</mirrorOf> <url>https://repo.sprin…
阅读更多...
C++ 12 之 指针引用

C++ 12 之 指针引用

c12指针引用.cpp #include <iostream>using namespace std;struct students12 {int age; };int main() {students12 stu;students12* p &stu; // 结构体指针students12* &pp p; // 结构体指针起别名pp->age 20;// (*pp).age 22;cout << "…
阅读更多...
sqli-labs 靶场 less-7 第七关详解：OUTFILE注入与配置

sqli-labs 靶场 less-7 第七关详解：OUTFILE注入与配置

SQLi-Labs是一个用于学习和练习SQL注入漏洞的开源应用程序。通过它&#xff0c;我们可以学习如何识别和利用不同类型的SQL注入漏洞&#xff0c;并了解如何修复和防范这些漏洞。Less 7 SQLI DUMB SERIES-7判断注入点 进入页面中&#xff0c;并输入数据查看结果。 发现空数据提…
阅读更多...
【Python】成功解决ModuleNotFoundError: No module named ‘PyQt5‘

【Python】成功解决ModuleNotFoundError: No module named ‘PyQt5‘

【Python】成功解决ModuleNotFoundError: No module named ‘PyQt5’ 下滑即可查看博客内容 &#x1f308; 欢迎莅临我的个人主页 &#x1f448;这里是我静心耕耘深度学习领域、真诚分享知识与智慧的小天地&#xff01;&#x1f387; &#x1f393; 博主简介&#xff1a;985…
阅读更多...
nodejs——原型链污染

nodejs——原型链污染

一、引用类型皆为对象 原型和原型链都是来源于对象而服务于对象的概念&#xff0c;所以我们要先明确一点&#xff1a; JavaScript中一切引用类型都是对象&#xff0c;对象就是属性的集合。 Array类型、Function类型、Object类型、Date类型、RegExp类型等都是引用类型。 也就…
阅读更多...
WPS JSA 宏脚本入门和样例

WPS JSA 宏脚本入门和样例

1入门 WPS window版本才支持JSA宏的功能。 可以自动化的操作文档中的一些内容。 参考文档&#xff1a; WPS API 参考文档&#xff1a;https://open.wps.cn/previous/docs/client/wpsLoad 微软的Word API文档&#xff1a;Microsoft.Office.Interop.Word 命名空间 | Microsoft …
阅读更多...
Latex | 数学公式

Latex | 数学公式

Latex 最近在学习使用 LaTeX 来敲公式&#xff0c;写材料。说实话&#xff0c;这个工具在写公式方面&#xff0c;确实堪称神器&#xff01;不只是我&#xff0c;连爱因斯坦要是看到它&#xff0c;估计都会点个赞。 在这里&#xff0c;我也得给大家分享一个宝藏网址&#xff1…
阅读更多...
SolidWorks官方授权代理商亿达四方带您解读最新SW版本特性

SolidWorks官方授权代理商亿达四方带您解读最新SW版本特性

在快速迭代的工业设计领域&#xff0c;每一次软件的更新都预示着生产力的跃升和设计边界的拓展。作为行业领先的3D CAD解决方案&#xff0c;SolidWorks的最新版本再次站在了技术创新的前沿&#xff0c;为企业和设计师们带来了前所未有的设计效率与创意自由度。亿达四方&#xf…
阅读更多...
LeakSearch：针对网络公开凭证的安全扫描与检测工具

LeakSearch：针对网络公开凭证的安全扫描与检测工具

关于LeakSearch 在红队演戏过程中&#xff0c;往往需要获取到针对目标域的访问权限。在这个过程中&#xff0c;很多红队人员会选择使用暴露在互联网上的代理服务器来实现目标域的访问&#xff0c;那么此时就需要在互联网上收集公开暴露的凭证信息。 对于蓝队来说&#xff0c;…
阅读更多...
每日5题Day23 - LeetCode 111 - 115

每日5题Day23 - LeetCode 111 - 115

每一步向前都是向自己的梦想更近一步&#xff0c;坚持不懈&#xff0c;勇往直前&#xff01; 第一题&#xff1a;111. 二叉树的最小深度 - 力扣&#xff08;LeetCode&#xff09; /*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeN…
阅读更多...
python的%time 、%%time 、%timeit、%%timeit的区别

python的%time 、%%time 、%timeit、%%timeit的区别

%time 、%timeit 要在ipython下才可以使用。（所以说Jupyter Notebook当然是可以用的，pycharm里的python环境也是jupyter Notebook的） %time可以测量一行代码执行的时间 %timeit可以测量一行代码多次执行的时间 网上有说法说，%timeit是测量一行代码100000次循环内，3次最快速…
阅读更多...
Vulnhub-DC-1,7

Vulnhub-DC-1,7

靶机IP:192.168.20.141 kaliIP:192.168.20.128 网络有问题的可以看下搭建Vulnhub靶机网络问题(获取不到IP) 前言 1和7都是Drupal的网站&#xff0c;只写了7&#xff0c;包含1的知识点 信息收集 用nmap扫描端口及版本号 进入主页查看作者给的提示&#xff0c;不是暴力破解的…
阅读更多...
PostgreSQL学习笔记

PostgreSQL学习笔记

一、安装 官网下载地址&#xff1a;EDB: Open-Source, Enterprise Postgres Database Management 双击安装程序进行安装 选择端口&#xff0c;默认的即可 验证是否安装成功 在开始菜单里找到PGAdmin 4 打开这个大象头&#xff0c;会在浏览器中打开新的标签页。第一次打开会…
阅读更多...
【vue-8】记事本案例

【vue-8】记事本案例

小知识点&#xff1a; 列表末尾插入数据&#xff1a; list.push("lihua") 列表删除数据&#xff1a; # index要删除数据的索引值&#xff0c;1为删除数据长度 list.splice(index,1) 完整示例代码&#xff1a; <!DOCTYPE html> <html lang"en&quo…
阅读更多...
Vue3+Vite报错：vite忽略.vue扩展名 Failed to resolve import ..... Does the file exist?

Vue3+Vite报错：vite忽略.vue扩展名 Failed to resolve import ..... Does the file exist?

Vue3Vite报错&#xff1a;vite忽略.vue扩展名 Failed to resolve import … Does the file exist? 先看报错&#xff1a; 分析原因 原因是我们没有写后缀名 建议你在你的vite.config.js中加上如下配置 import { defineConfig } from "vite"; import vue from &qu…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023