为什么电容两端电压不能突变

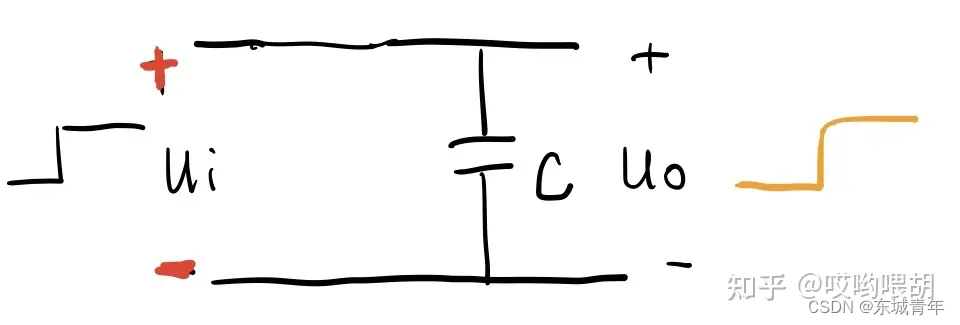
我们先从RC延时电路说起吧，图1是最简单的RC延时电路， $u_{i}$ 给一个阶跃的电压信号， $u_{o}$ 电压会变成黄色曲线这个样子，这是为什么呢？

$u_{i}$ 电压跳变后，电源负极电子移动到电容下极板，排斥上极板电子流动到电源正极。由于电阻R的存在，电子不能一股脑全部瞬间到达电源正极。因为电阻的作用就是限流=限制电子流动。一大波电子要一起从R的右侧跑到左侧，电阻说：不行，不管你们（电子）之前走的什么康庄大道（如4车道、8车道），到我这变成单向2车道了。电子没办法，只能放慢整体移动速度。

$u_{o}$ 电压是什么呀？1C仑电子在电容下极板与上极板之间的电势能差值。具体反应的就是电容下极板中获得的单身电子的数量多寡。

因为上极板电子在电阻的交通管制下，是慢慢从上极板跑到电源正极的，下极板的单身电子也是慢慢增加的，所以 $u_{o}$ 的电压曲线也是慢慢上升的。直到上升到电容板下极电子排斥力与上极板单身正正电荷的吸引力相等时，充电完成。

电阻R越大，交通管制越严重，电子整体移动速度越慢， $u_{o}$ 电压上升越慢，导致充电过程用时越长，即RC延时更久。电容C越大（电容也称电容量，是指在给定电位差下自由电荷的储藏量，即给定电位差U下，达到存储电量Q需要吸收或释放的电子个数C，即Q=C*U。）相同个数的电子移动到电源正极，即电子带的电量相同的情况下，C越大，U越小，所以C越大也导致充电过程时长越长，反之R越小，C越小，充电过程用时越短，即RC演示越短。

$RC=\frac{U}{I}*\frac{Q}{U}=\frac{Q}{I}=t$

如果R减小接近于0呢？

也就是图2这种情况，R消失了，但我们知道导线也不是超导体，存在着很小很小的电阻。所以即便电容很大，需要移动很多电子到电源正极才能完成电容充电，但电子几乎是在一条无障碍的大道上运动（因为电阻很小），还是几乎能瞬间到达电源正极（只能说几乎，毕竟还是有点电阻的）。所以此时 $u_{o}$ 的电压曲线如图2黄线这样，仅仅比 $u_{i}$ 圆润而已，不仔细看还以为电压突变了。

注意这里 $u_{o}$ 电压没有突变，只是因为电阻太小，电子跑到正极太快，导致电容两端电压上升太快，但绝不是突变啊。数学上突变的定义是有一处斜率为无穷大，是一个不连续点，如电容充电电流i，但这里 $u_{o}$ 电压仅仅是上升斜率很大，但斜率仍然是个有界值， $u_{o}$ 电压仍是连续函数。