1 Introduction

diffusion model 在多个领域有了突破，这篇文章从优化的角度来介绍diffusion，包括理论和代码。

2 Training diffusion models

diffusion 的样本集可以对应图像，音频，视频，机械臂轨迹，甚至是文本生成。

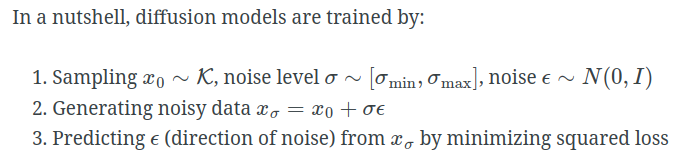
需要训练一个网络能生成noise direction。

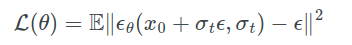
整体的训练就非常的简单，在原有数据集的基础上，添加噪声，然后模型要预测$ϵ$,去最小化误差。

def training_loop(loader  : DataLoader,model   : nn.Module,schedule: Schedule,epochs  : int = 10000):optimizer = torch.optim.Adam(model.parameters())for _ in range(epochs):for x0 in loader:optimizer.zero_grad()sigma, eps = generate_train_sample(x0, schedule)eps_hat = model(x0 + sigma * eps, sigma)loss = nn.MSELoss()(eps_hat, eps)optimizer.backward(loss)optimizer.step()
def generate_train_sample(x0: torch.FloatTensor, schedule: Schedule):sigma = schedule.sample_batch(x0)eps = torch.randn_like(x0)return sigma, eps

从lqg的角度来看这个问题
$$\begin{array}{rl}\dot{x}& =\end{array}$$

2.1 Noise Schedules

噪声强度并不是均匀的，而是定义了一个schedule

class Schedule:def __init__(self, sigmas: torch.FloatTensor):self.sigmas = sigmasdef __getitem__(self, i) -> torch.FloatTensor:return self.sigmas[i]def __len__(self) -> int:return len(self.sigmas)def sample_batch(self, x0:torch.FloatTensor) -> torch.FloatTensor:return self[torch.randint(len(self), (x0.shape[0],))].to(x0)class ScheduleLogLinear(Schedule):def __init__(self, N: int, sigma_min: float=0.02, sigma_max: float=10):super().__init__(torch.logspace(math.log10(sigma_min), math.log10(sigma_max), N))

前面可以糊的慢一点，后面糊的快一点
用一个非常简单的模型来做一个任务：

def get_sigma_embeds(sigma):sigma = sigma.unsqueeze(1)return torch.cat([torch.sin(torch.log(sigma)/2),torch.cos(torch.log(sigma)/2)], dim=1)class TimeInputMLP(nn.Module):def __init__(self, dim, hidden_dims):super().__init__()layers = []for in_dim, out_dim in pairwise((dim + 2,) + hidden_dims):layers.extend([nn.Linear(in_dim, out_dim), nn.GELU()])layers.append(nn.Linear(hidden_dims[-1], dim))self.net = nn.Sequential(*layers)self.input_dims = (dim,)def rand_input(self, batchsize):return torch.randn((batchsize,) + self.input_dims)def forward(self, x, sigma):sigma_embeds = get_sigma_embeds(sigma)         # shape: b x 2nn_input = torch.cat([x, sigma_embeds], dim=1) # shape: b x (dim + 2)return self.net(nn_input)model = TimeInputMLP(dim=2, hidden_dims=(16,128,128,128,128,16))

完整的代码

from smalldiffusion import (TimeInputMLP, ScheduleLogLinear, training_loop, samples,DatasaurusDozen, Swissroll
)
from torch.utils.data import DataLoader
import torch
import math
import torch.nn as nn
from itertools import pairwiseclass Schedule:def __init__(self, sigmas: torch.FloatTensor):self.sigmas = sigmasdef __getitem__(self, i) -> torch.FloatTensor:return self.sigmas[i]def __len__(self) -> int:return len(self.sigmas)def sample_batch(self, x0: torch.FloatTensor) -> torch.FloatTensor:return self[torch.randint(len(self), (x0.shape[0],))].to(x0.device)class ScheduleLogLinear(Schedule):def __init__(self, N: int, sigma_min: float=0.02, sigma_max: float=10):super().__init__(torch.logspace(math.log10(sigma_min), math.log10(sigma_max), N))def training_loop(loader: DataLoader,model: nn.Module,schdule: Schedule,epochs: int = 10000):optimizer = torch.optim.Adam(model.parameters())device = torch.device("cuda" if torch.cuda.is_available() else "cpu")model.to(device)for i in range(epochs):for x0 in loader:# 读取数据，并进行处理x0 = x0.to(device)optimizer.zero_grad()sigma, eps = generate_train_sample(x0, schdule)x = x0 + sigma.unsqueeze(1) * epseps_hat = model(x, sigma)# print(f'x.shape is {x.shape}, eps hat shape is {eps_hat.shape}, eps shape is {eps.shape}')loss = nn.MSELoss()(eps_hat, eps)loss.backward()optimizer.step()yield dict(loss=loss)if i % 1000 == 0:print(f'{i} / {epochs}, loss is: {loss}')# 对每个点都进行随机生成sigma
def generate_train_sample(x0: torch.FloatTensor, schdule: Schedule):sigmas = schdule.sample_batch(x0)eps = torch.randn_like(x0)return sigmas, epsdef get_sigma_embeds(sigma):sigma = sigma.unsqueeze(1)#sigma=10,return torch.cat([torch.sin(torch.log(sigma)/2),torch.cos(torch.log(sigma)/2)], dim=1)class TimeInputMLP(nn.Module):def __init__(self, dim, hidden_dims):super().__init__()layers = []for in_dim, out_dim in pairwise((dim + 2,) + hidden_dims):layers.extend([nn.Linear(in_dim, out_dim), nn.GELU()])layers.append(nn.Linear(hidden_dims[-1], dim))self.net = nn.Sequential(*layers)self.input_dims = (dim,)def rand_input(self, batch_size):# 随机生成这样的数据return torch.randn((batch_size,) + self.input_dims)def forward(self, x, sigma):sigma_embeds = get_sigma_embeds(sigma)nn_input = torch.cat([x, sigma_embeds], dim=1)return self.net(nn_input)dataset = DatasaurusDozen(csv_file='DatasaurusDozen.tsv', dataset='dino')
loader = DataLoader(dataset, batch_size=2130)
schedule = ScheduleLogLinear(N=200, sigma_min=0.005, sigma_max=10)
model = TimeInputMLP(dim=2, hidden_dims=(16, 128, 128, 128, 128, 16))
trainer = training_loop(loader, model, schedule, epochs=15000)
losses = [ns['loss'].item() for ns in trainer]

3 Denoising as approximate projection

认为learned denoiser 在预测数据manifold k的大致投影，diffusion的过程是最小化于manifold的距离，采用了relative-error approximation model 去分析diffusion sampling algorithms的收敛性。

3.1 基础知识

点x到分布k的距离，可以看成是点x到分布的最小距离

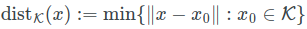
点x在分布上的投影，可以看成分布上有一点x0，和x的距离最小



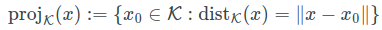
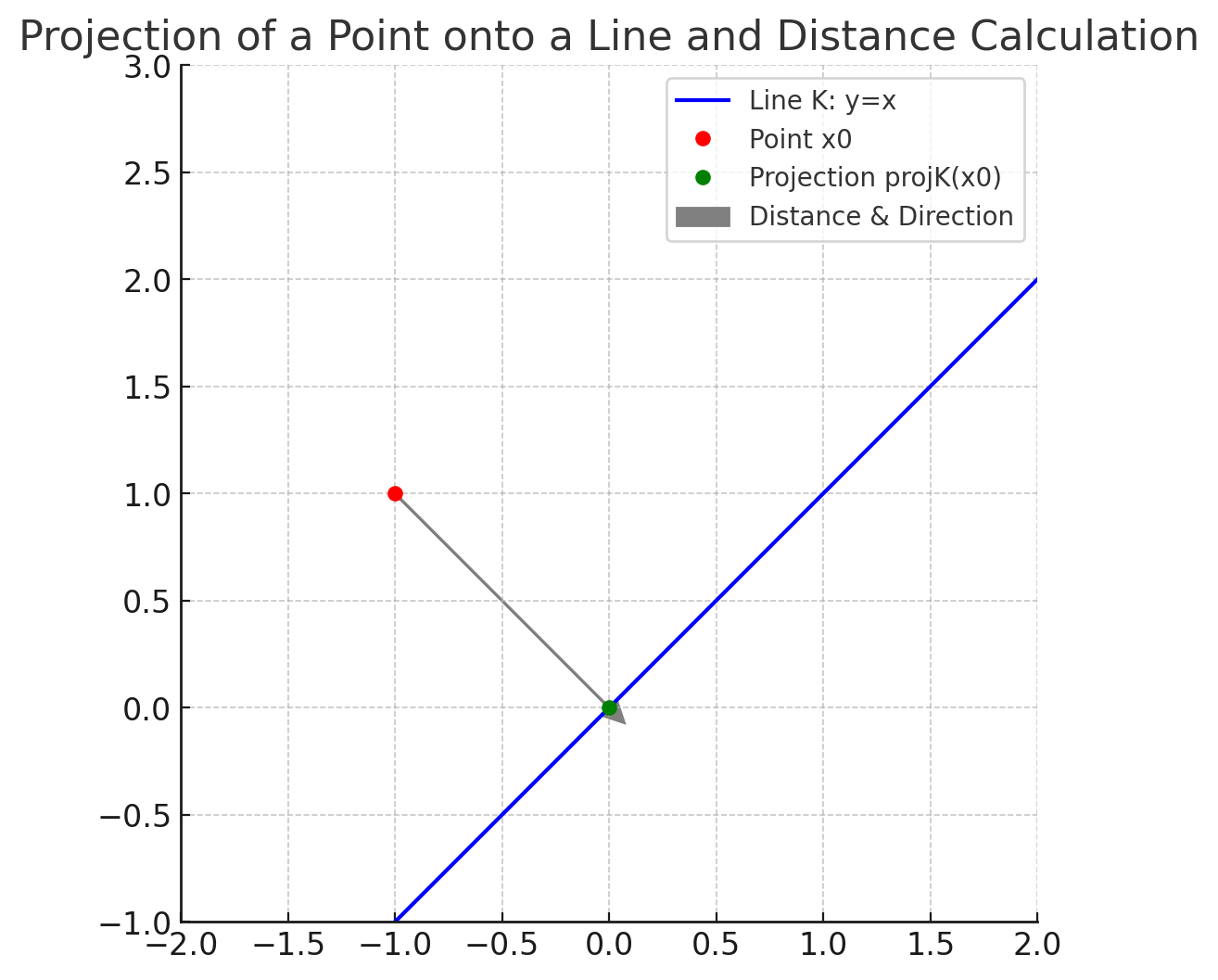
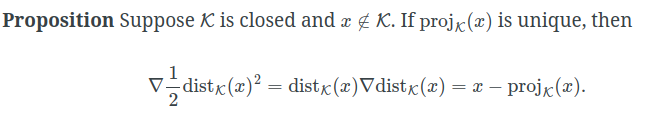
$\nabla dis{t}_k(x)$就是点到分布的方向(最速方向)，$dis{t}_k(x)$点到分布的距离，所以能得到上面这个定理。

有一个非常重要的技巧，很有可能是无法直接计算$dis{t}_k(x)$,用softmin去计算

def softmin(x, K, sigma):weights = np.exp(-((x - K)**2) / (2 * sigma**2))weighted_sum = np.sum(weights * (x - K)**2)total_weight = np.sum(weights)return np.sqrt(weighted_sum / total_weight)

3.2 ideal denoiser

完美的denoiser可以计算出最佳的方向，

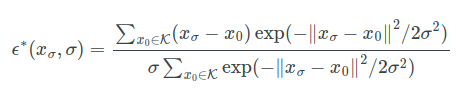
对于固定的sigma理想的denoiser的效果等价于

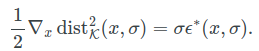
diffusion training的目标函数，等价于smoothed squared-distance function.

3.3 relative error model

使用了一种工具来分析收敛性
$$||x-\sigma {ϵ}_{\theta }(x,\sigma )-pro{j}_k(x)||\le \eta dis{t}_k(x)$$

这个不等式确实与 trust region 优化中的思想有些相似之处。让我们仔细分析一下:

1. 在 trust region 优化中,我们通过限制每次迭代的步长来控制近似模型的质量。类似地,这里的不等式限制了去噪过程中每一步的"误差",即去噪结果 $x-\sigma {ϵ}_{\theta }(x,\sigma )$ 与真实数据投影 ${\text{proj}}_K(x)$ 之间的距离。
2. 不等式右侧的 $\eta {\text{dist}}_K(x)$ 可以看作是一个自适应的"信任域半径"。当前噪声样本 $x$ 距离真实数据流形 $K$ 越远 (即 ${\text{dist}}_K(x)$ 越大),我们允许的去噪"误差"就越大。这与 trust region 优化中根据模型质量自适应调整信任域半径的思想类似。
3. 参数 $\eta$ 控制了"信任域"的大小,类似于 trust region 方法中的超参数。$\eta$ 需要适当选择:太大会导致去噪过程不稳定,太小则会使收敛速度变慢。
4. 不等式约束确保了去噪结果 $x-\sigma {ϵ}_{\theta }(x,\sigma )$ 始终在以真实数据投影 ${\text{proj}}_K(x)$ 为中心、以 $\eta {\text{dist}}_K(x)$ 为半径的球形"信任域"内。这防止了去噪过程中出现过大的偏移。
5. 在实际应用中,我们并不知道真实数据分布 $K$ 和投影 ${\text{proj}}_K(x)$,因此无法直接验证这个不等式。但是,如果去噪器 ${ϵ}_{\theta }$ 被很好地训练,这个不等式应该在较高置信度下成立。这就像在 trust region 优化中,我们假设局部模型在信任域内是一个良好的近似。
   总的来说,这个不等式反映了扩散模型中去噪过程的一个重要特性:每一步去噪应该是"可信"的,去噪结果不应该偏离真实数据太远。这与 trust region 优化中控制每次迭代步长、确保迭代过程稳定收敛的思想有异曲同工之妙。

这个不等式 $\frac{1}{\nu }{\text{dist}}_K(x)\le \sqrt{n}\sigma \le \nu {\text{dist}}_K(x)$ 对于理解扩散模型的采样过程非常重要。让我们详细分析一下它的含义和作用:

1. 不等式的中间项 $\sqrt{n}\sigma$ 表示噪声的标准差。回忆一下,在扩散模型中,我们通过逐步添加高斯噪声将数据分布 $x_0\sim q(x_0)$ 转化为易于采样的先验分布 $x_T\sim \mathcal{N}(0,{\sigma }_T^{2}I)$。这里的 $\sigma$ 就是控制这个噪声化过程的关键参数。

2. 不等式的左右两项都涉及到 ${\text{dist}}_K(x)$,即当前噪声样本 $x$ 到真实数据流形 $K$ 的距离。这个距离度量了去噪过程的进展:${\text{dist}}_K(x)$ 越小,说明 $x$ 越接近真实数据。

3. 参数 $\nu \ge 1$ 是一个常数,它控制了噪声标准差 $\sqrt{n}\sigma$ 与数据流形距离 ${\text{dist}}_K(x)$ 之间的相对大小。$\nu$ 的选择会影响去噪过程的稳定性和效率。

4. 不等式的左半部分 $\frac{1}{\nu }{\text{dist}}_K(x)\le \sqrt{n}\sigma$ 确保噪声水平 $\sigma$ 不会太小。直观地说,如果 $\sigma$ 太小,去噪过程就会变得不稳定,因为去噪器 ${ϵ}_{\theta }(x,\sigma )$ 需要从非常小的噪声中恢复出清晰的数据,这是一个病态问题(ill-posed problem)。

5. 不等式的右半部分 $\sqrt{n}\sigma \le \nu {\text{dist}}_K(x)$ 确保噪声水平 $\sigma$ 不会太大。如果 $\sigma$ 太大,去噪过程就会变得低效,因为我们需要非常多的去噪步骤才能从高度噪声化的样本中恢复出清晰的数据。

6. 总的来说,这个不等式提供了一个噪声水平 $\sigma$ 的"可行区间"。它确保噪声水平与样本到数据流形的距离相适应,从而在去噪的稳定性和效率之间取得平衡。在设计扩散模型的采样算法时,我们需要适当选择噪声水平序列 { σ t } t = 1 T \{\sigma_t\}_{t=1}^T {σt​}t=1T​,使其在整个去噪过程中满足这个不等式。

7. 在实践中,我们通常根据数据的维度 $n$ 和所需的采样质量来设置参数 $\nu$ 和噪声水平序列 { σ t } t = 1 T \{\sigma_t\}_{t=1}^T {σt​}t=1T​。然后,我们可以通过监测每一步的 ${\text{dist}}_K(x_t)$ 来验证不等式是否得到满足,并据此调整算法的超参数。

总之,这个不等式为设计和优化扩散模型的采样算法提供了重要的理论指导。它揭示了噪声水平、数据维度和去噪进度之间的内在联系,有助于我们更好地理解和控制扩散模型的去噪过程。
在采样的起始阶段,我们从先验分布 $x_T\sim \mathcal{N}(0,{\sigma }_T^{2}I)$ 采样一个高度噪声化的样本。此时,样本 $x_T$ 距离真实数据流形 $K$ 很远,即 ${\text{dist}}_K(x_T)$ 很大。为了稳定和高效地去噪,我们需要选择一个较大的噪声水平 ${\sigma }_T$,使其满足不等式的右半部分 $\sqrt{n}{\sigma }_T\le \nu {\text{dist}}_K(x_T)$。
在采样的中间阶段,我们逐步去噪,样本 $x_t$ 逐渐接近真实数据流形 $K$。为了维持去噪的稳定性和效率,我们需要适当降低噪声水平 ${\sigma }_t$,使其始终满足不等式 $\frac{1}{\nu }{\text{dist}}_K(x_t)\le \sqrt{n}{\sigma }_t\le \nu {\text{dist}}_K(x_t)$。这确保了噪声水平与样本到数据流形的距离相适应。
在采样的末尾阶段,样本 $x_t$ 已经非常接近真实数据流形 $K$,即 ${\text{dist}}_K(x_t)$ 很小。为了最终得到高质量的样本,我们需要选择一个较小的噪声水平 ${\sigma }_t$,使其满足不等式的左半部分 $\frac{1}{\nu }{\text{dist}}_K(x_t)\le \sqrt{n}{\sigma }_t$。

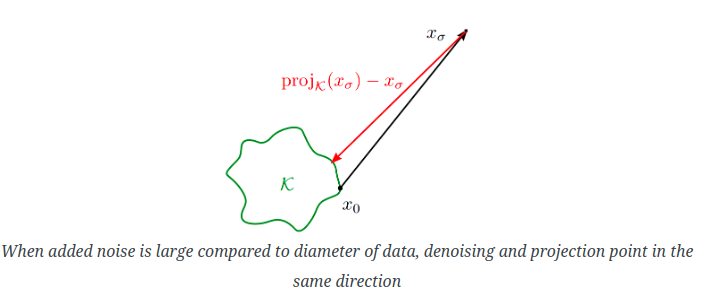
对于大部分情况来说，denoising就是找projection.

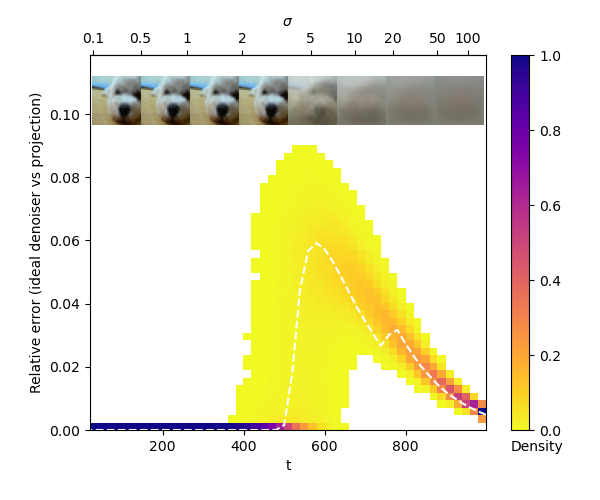
这个图展示了在CIFAR-10数据集上,理想去噪器(ideal denoiser)在相对误差模型下的表现。横轴表示扩散过程的时间步 $t$,纵轴表示理想去噪器输出与真实数据投影之间的相对误差。

在 $\sigma$ 很小(即 $t$ 接近0)或很大(即 $t$ 接近1000)时,相对误差都较小,这可以从以下两个角度解释:

1. 当 $\sigma$ 很小时,扩散过程刚开始,噪声样本 $x_t$ 与真实数据 $x_0$ 非常接近。此时,去噪非常容易,因为去噪器只需要去除很小的噪声。即使去噪结果与真实数据投影有一定偏差,相对误差也会很小。

2. 当 $\sigma$ 很大时,扩散过程接近尾声,噪声样本 $x_t$ 基本上完全被噪声主导。在这种情况下,去噪器的最优策略是直接预测数据的均值(即数据流形 $K$ 上的一个中心点),而不是试图恢复每个样本的细节。这个均值预测通常与真实数据投影 ${\text{proj}}_K(x_t)$ 很接近,因此相对误差也很小。

相比之下,在中间阶段(即 $\sigma$ 适中时),相对误差达到最大。这是因为此时的去噪任务最具挑战性:噪声样本 $x_t$ 既包含真实数据的信息,也受到相当大的噪声干扰。去噪器需要在去除噪声的同时保留数据的细节,这是一个微妙的平衡。因此,去噪结果与真实数据投影之间的相对误差会较大。

总的来说,这个图验证了我们之前讨论的不等式 $\frac{1}{\nu }{\text{dist}}_K(x)\le \sqrt{n}\sigma \le \nu {\text{dist}}_K(x)$ 的含义。在扩散过程的起始阶段和末尾阶段,噪声水平 $\sigma$ 分别较大和较小,去噪相对容易;而在中间阶段,噪声水平 $\sigma$ 适中,去噪最具挑战性。这启发我们在设计采样算法时,需要根据样本的噪声水平适应性地调整去噪策略,以达到最佳的去噪效果。
使用ideal dignoser 进行轨迹重建的完整代码

from smalldiffusion import (TimeInputMLP, ScheduleLogLinear, training_loop, samples,DatasaurusDozen, Swissroll
)
from torch.utils.data import DataLoader
import torch
import math
import torch.nn as nn
from itertools import pairwise
import numpy as npclass Schedule:def __init__(self, sigmas: torch.FloatTensor):self.sigmas = sigmasdef __getitem__(self, i) -> torch.FloatTensor:return self.sigmas[i]def __len__(self) -> int:return len(self.sigmas)def sample_batch(self, x0: torch.FloatTensor) -> torch.FloatTensor:return self[torch.randint(len(self), (x0.shape[0],))].to(x0.device)def sample_sigmas(self, steps: int) -> torch.FloatTensor:indices = list((len(self) * (1 - np.arange(0, steps)/steps)).round().astype(np.int64) - 1)return self[indices + [0]]class ScheduleLogLinear(Schedule):def __init__(self, N: int, sigma_min: float=0.02, sigma_max: float=10):super().__init__(torch.logspace(math.log10(sigma_min), math.log10(sigma_max), N))# ideal denoiser
def sq_norm(M, k):# M: b x n --(norm)--> b --(repeat)--> b x kreturn (torch.norm(M, dim=1)**2).unsqueeze(1).repeat(1,k)class IdealDenoiser:def __init__(self, dataset: torch.utils.data.Dataset):self.data = torch.stack(list(dataset))self.input_dims = (self.data.shape[-1],)print(f'input_dims is: {self.input_dims}' )self.data = self.data[0]print(f'self data shape: {self.data.shape}')def __call__(self, x, sigma):x = x.flatten(start_dim=1)d = self.data.flatten(start_dim=1)xb, db = x.shape[0], d.shape[0]sq_diffs = sq_norm(x, db) + sq_norm(d, xb).T - 2 * x @ d.Tweights = torch.nn.functional.softmax(-sq_diffs/2/sigma**2, dim=1)return (x - torch.einsum('ij,j...->i...', weights, self.data))/sigmadef rand_input(self, batch_size):# 随机生成这样的数据return torch.randn((batch_size,) + self.input_dims)
@torch.no_grad()
def samples(denoiser   : IdealDenoiser,sigmas     : torch.FloatTensor, # Iterable with N+1 values for N sampling stepsgam        : float = 1.,        # Suggested to use gam >= 1mu         : float = 0.,        # Requires mu in [0, 1)batchsize  : int = 1):xt = denoiser.rand_input(batchsize) * sigmas[0]eps = Nonefor i, (sig, sig_prev) in enumerate(pairwise(sigmas)):eps, eps_prev = denoiser(xt, sig), epseps_av = eps * gam + eps_prev * (1-gam)  if i > 0 else epssig_p = (sig_prev/sig**mu)**(1/(1-mu)) # sig_prev == sig**mu sig_p**(1-mu)eta = (sig_prev**2 - sig_p**2).sqrt()xt = xt - (sig - sig_p) * eps_av + eta * denoiser.rand_input(batchsize).to(xt)yield xt
import numpy as np
schedule = ScheduleLogLinear(N=200, sigma_min=0.005, sigma_max=10)
dataset = Swissroll(np.pi/2, 5*np.pi, 100)
loader = DataLoader(dataset, batch_size=2000)
denoiser = IdealDenoiser(loader)
batchsize = 2000
sigmas = schedule.sample_sigmas(20)
generator = samples(denoiser, sigmas, gam=2, mu=0, batchsize=batchsize)
# 遍历生成器并可视化每个步骤的结果
import matplotlib.pyplot as plt
for i, xt in enumerate(generator):plt.scatter(xt[:, 0], xt[:, 1])plt.title(f'Step {i+1}')plt.show()

3.3 Sampling from diffusion models

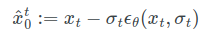
通过迭代的方式逐步去收敛，首先
$(X_T,{\sigma }_T)$, $dis{t}_k(X_T)/\sqrt{(}n)={\sigma }_T$
$X_T$可以从$N(0,{\sigma }_T)$中去采样
真实的数据在这里，通过逐渐的迭代，采样点最终能到projected point

这个图也很容易理解，图中$x_t-x_{t-1}$的模就是${\sigma }_{t-1}-{\sigma }_t$长度，${ϵ}_{\theta }$是方向

3.4 Diffusion sampling as distance minimization

squared-distance
$$f(x)=\frac{1}{2}dis{t}_k(x{)}^2$$

在DDIM中,步长的选择确实与我们之前讨论的 ${\sigma }_{t-1}-{\sigma }_t$ 有所不同。这里我尝试解释一下原因。

首先,让我们回顾一下扩散模型的核心思想。扩散模型通过逐步添加高斯噪声将复杂的数据分布转化为易于采样的先验分布,然后通过逐步去噪恢复原始数据。在连续时间的扩散过程中,这可以用如下的随机微分方程(SDE)来描述:

$$dx=-\frac{1}{2}\beta (t)x(t)dt+\sqrt{\beta (t)}dw$$

其中 $x(t)$ 表示时间 $t$ 的噪声样本,$w(t)$ 是标准维纳过程(即布朗运动),$\beta (t)$ 是噪声调度函数,控制扩散的速度。

DDIM的核心思想是将这个SDE离散化,并将其解释为关于平方距离函数 $f(x)=\frac{1}{2}{\text{dist}}_K(x{)}^2$ 的梯度下降。在这种解释下,每个去噪步骤可以看作是在 $f(x)$ 上沿负梯度方向下降,步长为 $1-{\sigma }_{t-1}/{\sigma }_t$。

那么,为什么要选择这个特定的步长呢?这与DDIM的一个重要性质有关:DDIM是非迭代的(non-iterative),意味着每个去噪步骤都直接从先前的噪声样本中采样,而不依赖于之前的去噪结果。这使得DDIM的去噪过程更加高效和稳定。

为了实现这一点,DDIM需要精心设计步长,使得相邻两个噪声样本 $x_t$ 和 $x_{t-1}$ 的分布之间的KL散度最小化。可以证明,$1-{\sigma }_{t-1}/{\sigma }_t$ 正是实现这一目标的最优步长。直观地说,这个步长确保了去噪过程在噪声水平高的地方(即 ${\sigma }_t$ 大的地方)迈出较大的步伐,而在噪声水平低的地方(即 ${\sigma }_t$ 小的地方)迈出较小的步伐,从而实现自适应的去噪速度控制。

总的来说,DDIM中步长的选择 $1-{\sigma }_{t-1}/{\sigma }_t$ 是出于理论最优性和算法稳定性的考虑。它与我们之前讨论的 ${\sigma }_{t-1}-{\sigma }_t$ 有所不同,但背后的直觉是一致的:步长应该与噪声水平相适应,在噪声大的地方迈大步,在噪声小的地方迈小步。这个原则对于设计高效稳定的去噪算法至关重要。
你的观察非常敏锐!DDIM和trust region优化之间确实有一些有趣的相似之处。让我们深入探讨一下这两者的联系。

Trust region优化是一种常用的非线性优化方法。它的基本思想是在每次迭代时,在当前点附近构建一个局部模型(通常是二次模型),然后在一个"信任域"内寻找全局最优解。这个信任域通常是一个以当前点为中心、以信任半径为半径的球形区域。信任半径在每次迭代后根据模型的准确性进行调整。

DDIM的去噪过程与trust region优化有以下几个相似之处:

1. 局部模型：在DDIM中,我们使用去噪器 ${ϵ}_{\theta }(x_t,{\sigma }_t)$ 来预测噪声样本 $x_t$ 的理想去噪方向。这可以看作是在 $x_t$ 附近构建了一个局部模型,用于指导去噪过程。类似地,trust region优化在每个迭代点附近构建一个局部二次模型。

2. 信任域：在DDIM中,步长 $1-{\sigma }_{t-1}/{\sigma }_t$ 控制了每个去噪步骤的大小。这个步长的选择确保了相邻两个噪声样本之间的KL散度最小化。从几何角度看,这相当于在噪声样本空间中定义了一个"信任域",去噪过程只在这个信任域内进行。类似地,trust region优化在每次迭代时都会定义一个信任域,优化过程被限制在这个信任域内。

3. 自适应步长：在DDIM中,步长 $1-{\sigma }_{t-1}/{\sigma }_t$ 会根据噪声水平自适应地调整。当噪声水平高时,步长较大;当噪声水平低时,步长较小。这确保了去噪过程在不同噪声水平下的稳定性和效率。类似地,trust region优化会根据局部模型的准确性自适应地调整信任半径。如果局部模型很准确,信任半径会增大;如果局部模型不准确,信任半径会减小。

4. 全局收敛：在DDIM中,通过逐步去噪,我们最终希望收敛到真实数据分布。这可以看作是在噪声样本空间中寻找一个全局最优解,即噪声最小、与真实数据最接近的样本。类似地,trust region优化通过逐步迭代,最终希望收敛到目标函数的全局最优解。

尽管DDIM和trust region优化在具体算法细节上有所不同,但它们的核心思想是一致的:在局部区域内构建简化模型,通过自适应步长控制迭代过程,最终实现全局收敛。这种局部到全局的优化策略在许多领域都有广泛应用,包括机器学习、最优控制、计算物理等。

从这个角度看,我们可以将DDIM理解为一种特殊的trust region优化算法,专门针对扩散模型中的去噪问题而设计。它巧妙地利用了扩散过程的概率性质,通过最小化KL散度来自适应地调整去噪步长,从而实现高效稳定的去噪。这一洞见不仅深化了我们对DDIM的理解,也为设计新的去噪算法提供了有益的启示。
选择合适的sampling schedule,

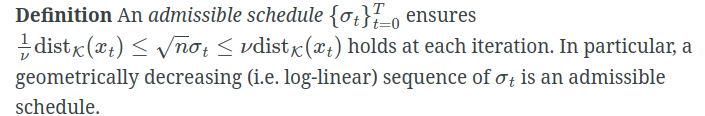
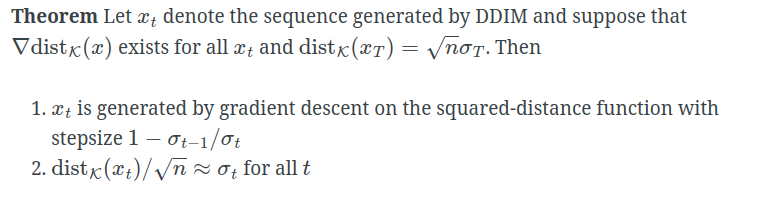
3.5 Improved sampler with gradient estimation

这个也很容易理解，利用方向的差值，作为对未来的预测，用作monentum这一项。


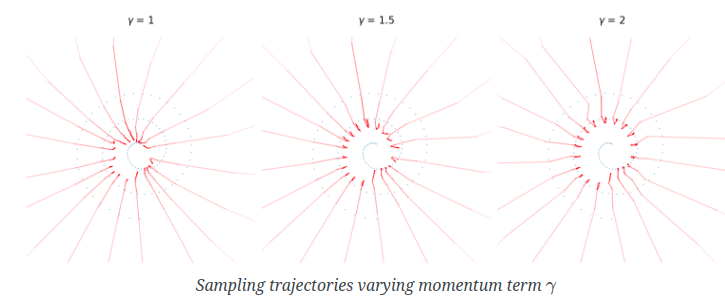
对应的代码

device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
batchsize = 2000
sigmas = schedule.sample_sigmas(20)
xt = model.rand_input(batchsize).to(device) * sigmas[0]
eps = None
gam = 2
mu = 0.0
for i, (sig, sig_prev) in enumerate(pairwise(sigmas)):sigma = torch.tensor(sig, device=device).repeat(xt.size(0))eps, eps_prev = model(xt, sigma), eps# print(f'eps is {eps}')eps_av = eps * gam + eps_prev * (1-gam)  if i > 0 else epssig_p = (sig_prev/sig**mu)**(1/(1-mu)) # sig_prev == sig**mu sig_p**(1-mu)eta = (sig_prev**2 - sig_p**2).sqrt()xt = xt - (sig - sig_p) * eps_av + eta * model.rand_input(batchsize).to(xt)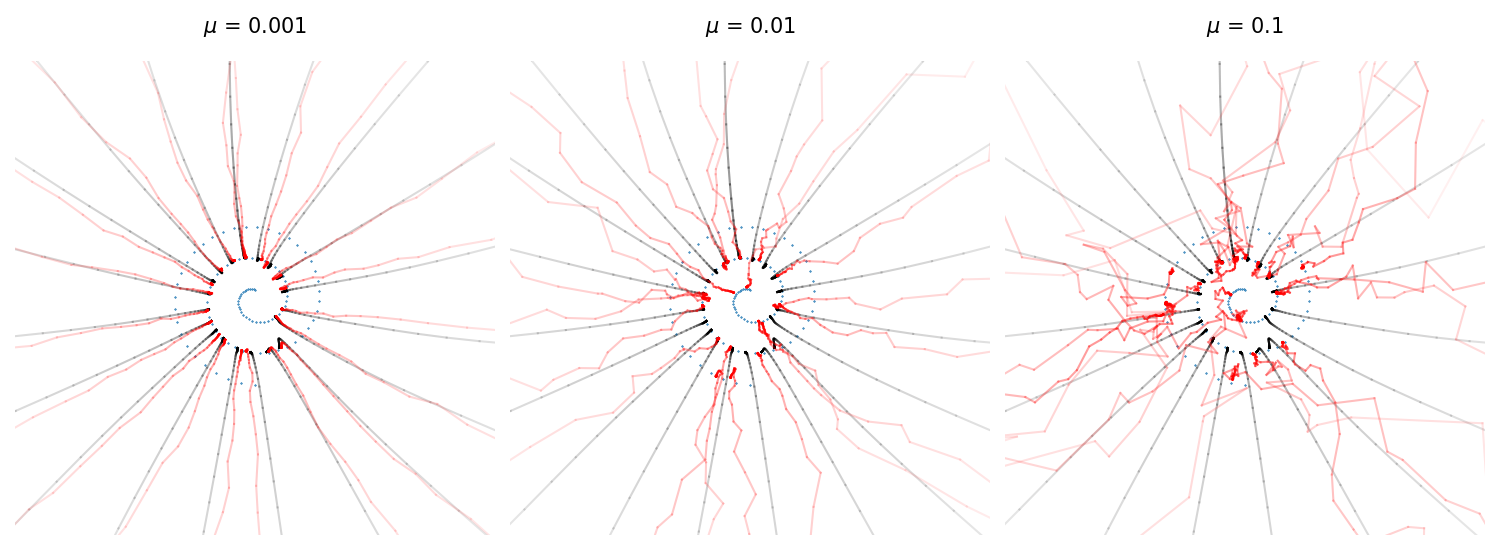

eta的设计目的是为了维持扩散模型的马尔可夫链结构,即确保每一步更新后的样本点仍然符合扩散模型的状态转移概率分布。具体来说,eta的表达式(sig_prev2 - sig_p2).sqrt()是根据扩散模型的理论推导得到的,它确保了在给定前一时刻样本点的条件下,当前时刻样本点的条件概率分布保持不变。
从直觉上理解,添加eta噪声的目的是为了在去噪的同时,引入一定的随机性和不确定性,防止去噪过程过于"决定论"而失去多样性。这种随机性可以帮助我们在去噪的过程中探索更多可能的路径,从而生成更加多样化和鲁棒的样本。
总的来说,eta的设计是基于扩散模型的理论基础,它在数学上确保了采样过程的马尔可夫性质。虽然添加eta噪声后的样本点分布与之前的分布并不完全相同,但这种差异是有目的和可控的。它在一定程度上牺牲了分布的精确匹配,换取了采样过程的稳定性、多样性和鲁棒性。

my_list1 = [[1, 2], [2, 3]]
M1= torch.tensor(my_list1, dtype=torch.float32)
k1 = 2
my_list2 = [[0, 0],[1, 1],[2, 2],]
k2 = 3
M2 = torch.tensor(my_list2, dtype=torch.float32)
result1 = sq_norm(M1, k2) + sq_norm(M2, k1).T - 2 * M1 @ M2.T
print(result1)

tensor([[ 5., 1., 1.],
[13., 5., 1.]])

torch.einsum(‘ij,j…->i…’, weights, self.data) 实际上就是weights@data，用来估计最近点的

References

[1] https://chenyang.co/diffusion.html
[2] https://github.com/yuanchenyang/smalldiffusion