c++_0基础_讲解7 练习

这一讲我为大家准备了几道题目，大家试着独自做一下（可能来自不同网站）

整数大小比较 - 洛谷

题目描述

输入两个整数，比较它们的大小。若 x>yx>y ，输出 > ；若 x=yx=y ，输出 = ；若 x<yx<y，输出 < 。

输入格式

一行，包含两个整数 xx 和 yy ，中间用单个空格隔开。 0≤x<232,−231≤y<2310≤x<232,−231≤y<231 。

输出格式

一个字符。若 x>yx>y，输出 > ；若 x=yx=y ，输出 = ；若 x<yx<y ，输出 < ；

输入输出样例

输入 #1复制

1000 100

输出 #1复制

首先我们看到数据范围,x 的大小有可能超过 int 的范围，所以我们要使用 long long 来存储。代码如下：#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
int main() {long long x, y;cin >> x >> y;if (x > y) {cout <<">";}if (x == y) {cout <<"=";}if (x < y) {cout <<"<";}return 0;
}

三角形判断 - 洛谷

题目描述

给定三个正整数，分别表示三条线段的长度，判断这三条线段能否构成一个三角形。

输入格式

输入共一行，包含三个正整数，分别表示三条线段的长度，数与数之间以一个空格分开。（三条边的长度均不超过 1000010000）

输出格式

如果能构成三角形，则输出 1 ，否则输出 0。

输入输出样例

输入 #1复制

1 1 1

输出 #1复制

输入 #2复制

1 1 3

输出 #2复制

说明/提示

构成三角形的条件：

任意两边长度之和大于第三条边的长度。

根据小学数学的知识可知，任意两边之和大于第三边，即可形成三角形，我们在程序中判断一下即可。

#include<bits/stdc++.h>
using namespace std;
int main() {int a,b,c;cin>>a>>b>>c;int mx=max(a,max(b,c));int sum=a+b+c;sum-=mx;if(sum>mx){cout<<1;}else cout<<0;
}

[语言月赛 202405] 最大的和 - 洛谷

题目描述

小 S 喜欢连在一起的数字，如果这些数字的和很大就更好了。

所以她现在要给你一个 n 行 n 列的网格 AA，第 i行第 j列上填有一个整数 Ai,j。

接下来你可以在 A上任取一行、一列或一条与任意对角线平行且只经过网格交叉点的直线（注意，不是线段），满足经过至少一个数字，且经过的数字之和最大。

如果对上面的表述有疑惑，请参考样例解释辅助理解。

你需要告诉小 S 这个最大的数字之和。

输入格式

输入共 n+1 行。

第一行，一个正整数 n，表示方阵的行数、列数。
接下来 n行，每行 n=n 个用空格隔开的整数，其中第 i行第 j个整数表示 Ai,j。

输出格式

输出一行一个整数，表示最大的数字之和。

输入输出样例

输入 #1复制

输出 #1复制

输入 #2复制

输出 #2复制

输入 #3复制

3
-1 -1 -1
-1 -1 -1
-1 -1 -1

输出 #3复制

-1

输入 #4复制

3
-100 -10 -100
-10 99999 -10
-100 -10 -100

输出 #4复制

说明/提示

样例 1 解释

对于样例 11，不难看出第 33 行数字之和最大，有 3+3+3=93+3+3=9。

样例 2 解释

对于样例 22，数字之和最大的，满足条件的线如下所示：

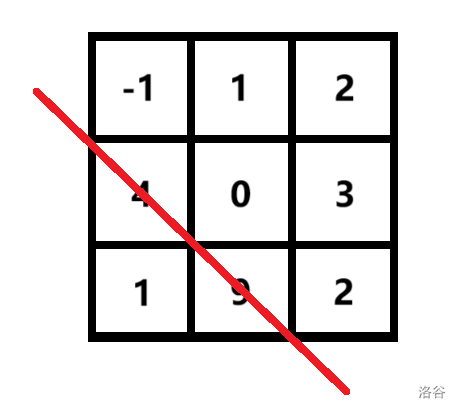
此时有 4+9=134+9=13。

注意，因为要求与对角线平行的直线只能经过网格交点，所以并不能出现同时取 4,1,94,1,9 或同时取 4,1,9,24,1,9,2 这样的情况。

样例 33 解释

取某条只经过一个 −1−1 的直线即为最大。注意，不可以一个数字都不选。

样例 44 解释

显然，取斜着的线一定不优，只能选择中间那一行或一列，答案是 −10+99999−10=99979−10+99999−10=99979。

数据范围

对于前 30%30% 的数据，保证 A1,1A1,1 或 An,nAn,n 的值为网格中唯一的非负整数。
对于另 20%20% 的数据，保证每一行数字相同，且最后一行中的数字之和为最大值。
对于另 20%20% 的数据，保证每一行数字相同，网格中不存在负数。
对于 100%100% 的数据，保证 1≤n≤2×103,−105≤Ai,j≤1051≤n≤2×103,−105≤Ai,j≤105。

题目大意

给定一个 n×nn×n 的方阵，请你取一行，一列，或者与对角线平行的一条只经过格点的直线，满足经过的数字和最大。

题目分析

首先，开一个二维数组 a 来存储方阵上的数字：

int a[2005][2005];

然后开两个变量 ans 和 res。 ans 代表最终答案，初始要赋值成一个很小的负数（比如 −1018−1018）；res 代表一个临时变量，用来统计某一行、某一列或某一斜线上的数字和。注意数据范围，要使用 long long 类型：

long long res, ans = -1e18;

接下来考虑求出答案。取一行、一列的情况是好写的。对于取一行的情况，我们可以循环枚举每一行，然后分别算出每一行的数字和，用数字和去更新答案。写法如下：

for(int i = 1; i <= n; i++) {res = 0;for(int j = 1; j <= n; j++)res += a[i][j];ans = max(ans, res);
}

取一列的情况同理，枚举列即可：

for(int i = 1; i <= n; i++) {res = 0;for(int j = 1; j <= n; j++)res += a[j][i];ans = max(ans, res);
}

接下来考虑如何求与对角线平行的情况。这里我们首先需要了解一个知识点：

考虑从左上到右下的对角线。对于任意一条与这个对角线平行的直线，其经过的所有格子的行数与列数之差一定相同。

我们这里画图来解释一下。

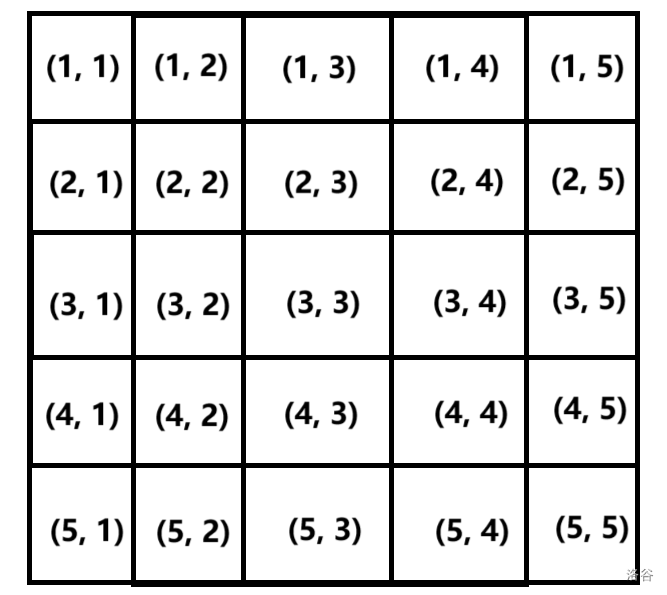
首先，这是一个 5×55×5 的方阵。我们随便取一条从左上到右下的满足条件的斜线：

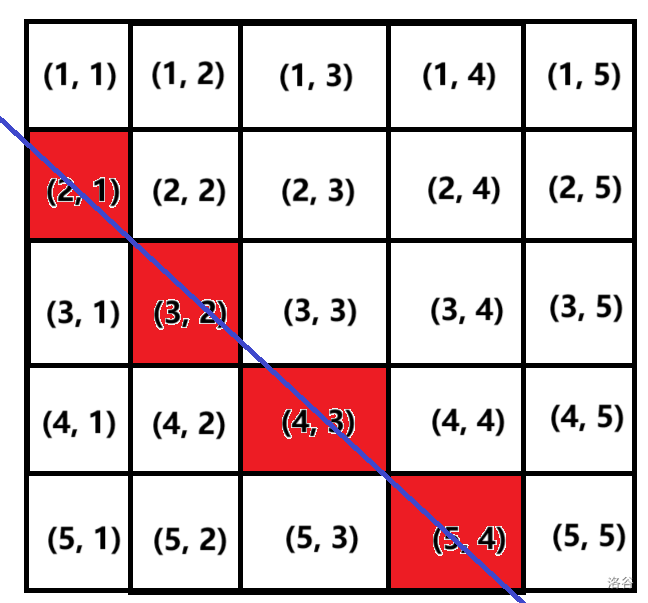
不难发现，(2,1),(3,2),(4,3),(5,4)(2,1),(3,2),(4,3),(5,4) 都满足行数 −− 列数 =1=1。大家也可以试试其它斜线，可以发现都满足上面的规律。

考虑从右上到左下的对角线。对于任意一条与这个对角线平行的直线，其经过的所有格子的行数与列数之和一定相同。

我们同样画图来解释一下。

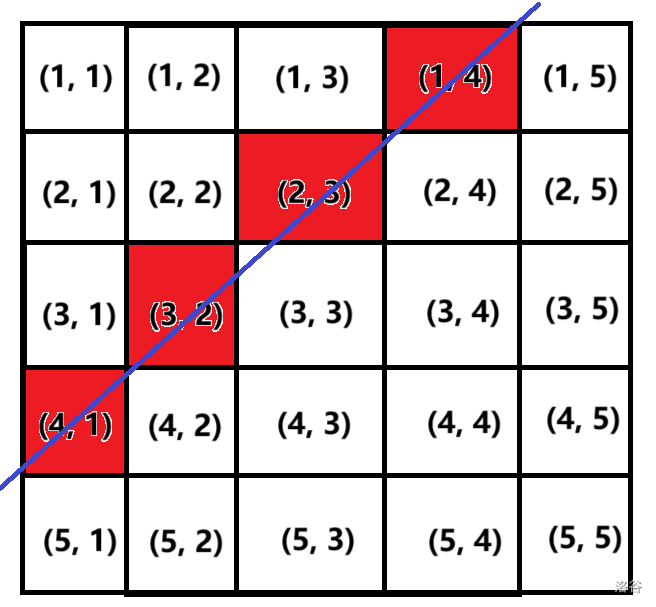
不难发现，(1,4),(2,3),(3,2),(4,1)(1,4),(2,3),(3,2),(4,1) 都满足行数 ++ 列数 =5=5。大家也可以试试其它斜线，可以发现都满足上面的规律。

因此，对于从左上到右下的斜线，我们可以选择枚举行数与列数的差，这样就相当于枚举了这条斜线。然后将斜线上的数字都加起来，去更新答案：

//这里 i 代表正在枚举的行数与列数的差（左上到右下）
//行和列的最小值都是 1，最大值都是 n，所以这个差值最小就是 1-n，最大是 n-1
for(int i = 1-n; i <= n-1; i++) {res = 0;//然后枚举这条线上所有格子的行数 j//那么此时列数就等于 j-ifor(int j = 1; j <= n; j++)//这里 j-i 还要判断范围，是因为要保证这个格子不能出界if(1 <= j-i && j-i <= n) res += a[j][j-i];ans = max(ans, res);
}

从右上到左下的斜线也类似：

//这里 i 代表正在枚举的行数与列数的和（右上到左下）
//行和列的最小值都是 1，最大值都是 n，所以这个和值最小就是 2，最大是 n+n
for(int i = 2; i <= n+n; i++) {res = 0;//然后枚举这条线上所有格子的行数 j//那么此时列数就等于 i-jfor(int j = 1; j <= n; j++)//这里 i-j 还要判断范围，是因为要保证这个格子不能出界if(1 <= i-j && i-j <= n) res += a[j][i-j];ans = max(ans, res);
}

最后输出答案即可：