目录
前言
E-R模型质量低的深层原因
数据依赖
函数依赖
主属性/非主属性
逻辑蕴含与闭包
Armstrong's Axiom
求解F闭包算法
求解属性集闭包算法
属性集闭包的作用
候选码求解理论和算法
候选码求解理论
无关属性
检验方法
正则覆盖
关系模式的设计
关系模式存在的问题
模式分解
范式
第一范式
第二范式
第三范式
练习题
BCNF
练习题
函数依赖综合练习题
总结
前言
前一周我们学习了E-R模型以及如何用E-R模型实现数据库设计。但是E-R模型设计数据库存在问题——–E-R模型质量和设计人员能力水平相关,质量难以保证
鉴于这样的问题,想要提出一种规范化的关系数据库设计方法——模式规范化方法(规范化数据库设计)
E-R模型质量低的深层原因
想要规范模式以提高模式质量,就要先明白为什么一个模式的质量高又为什么一个模式的质量低。通过研究发现:
模式质量低的原因:不合适的数据依赖
因此,规范化模式本质就是通过对模式规范化来消除不合适的数据依赖


数据依赖
定义:是数据间的一种相互关系,是数据的内在性质
影响:不合适的数据依赖导致不合适的数据之间相互纠缠造成数据不一致、冗余等问题。这些问题又将直接导致插入异常、删除异常、更新异常等异常现象

分类: 函数依赖、多值依赖、连接依赖、抽象依赖等

函数依赖
定义:

函数依赖研究的是一个关系模式中属性之间的依赖关系
课堂小题目:
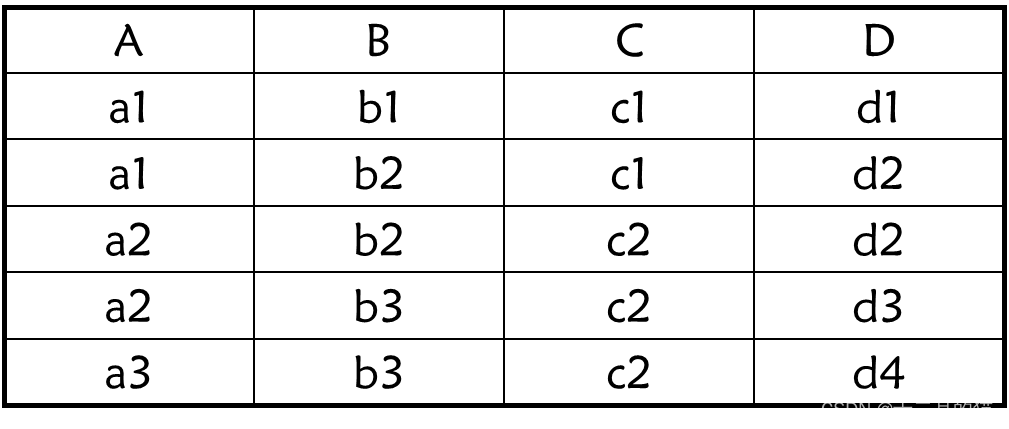
- A → C 成立
- C → A 不成立
- AB → D 成立
分类 :
1、平凡/非平凡函数依赖

平凡函数依赖就是必然存在的函数依赖关系(属性依赖关系)
2、部分/全部函数依赖 (多个属性的依赖关系)
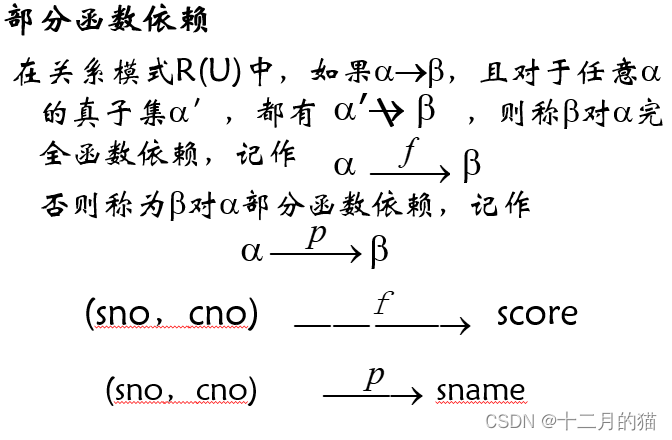
全部:共同决定;部分:只要其中一些就可以决定
这个函数依赖类型和第二范式息息相关
3、传递函数依赖

传递依赖满足:1、非平凡;2、非双向
传递依赖和第三范式息息相关
主属性/非主属性
定义:
注意!!主属性是候选码中的属性
逻辑蕴含与闭包
逻辑蕴含与闭包:

逻辑蕴含:扩充函数依赖集的动词,联系函数依赖集和函数依赖
通俗:如果给定一组函数依赖集F,够推导出其他的函数依赖集A,则说明F逻辑蕴含A
闭包:一个类型事物的全体化表示(F的闭包:F下的全体函数依赖;属性的集闭包:F下全体属性集)
通俗:函数依赖集F+由F能够推导出的所有其他函数依赖集A=F+
Armstrong's Axiom
问题:如何通过一组函数依赖集F去推导出其他的函数依赖A,从而知道F逻辑蕴含哪些函数依赖,并且得到F的闭包呢?
解决:Armstrong's Axiom公理系统
作用:利用公理系统,在函数依赖集F中求出全新的函数依赖
内容:

正确性以及完备性证明:
前提定义:
S1 = { f |可用Armstrong's Axiom从F中导出的函数依赖f }
S2 = { f |被F所逻辑蕴涵的函数依赖f }
问题数学化:
1、正确性(Sound):S1 ⊆ S2
2、完备性(Complete):S2 ⊆ S1
正确性:
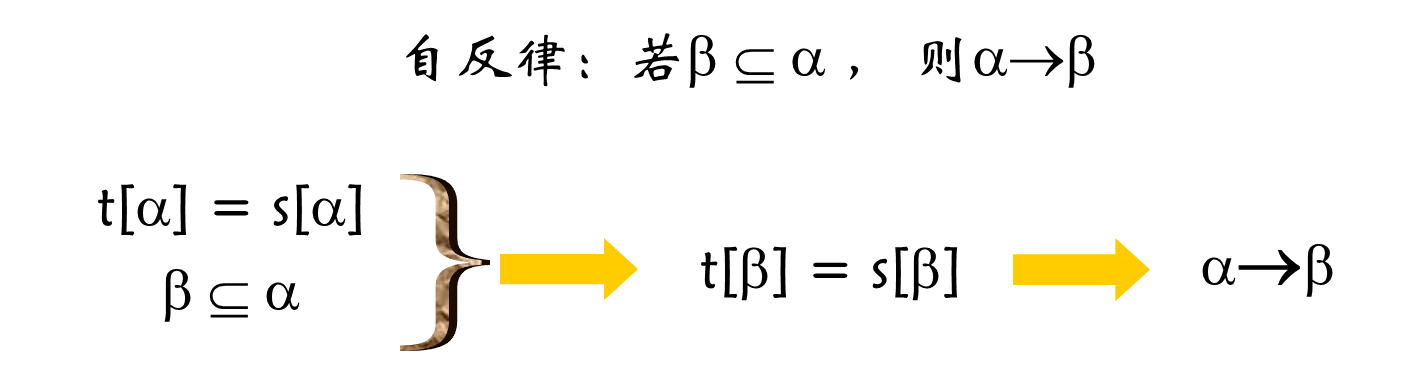
1、自反律的正确性:
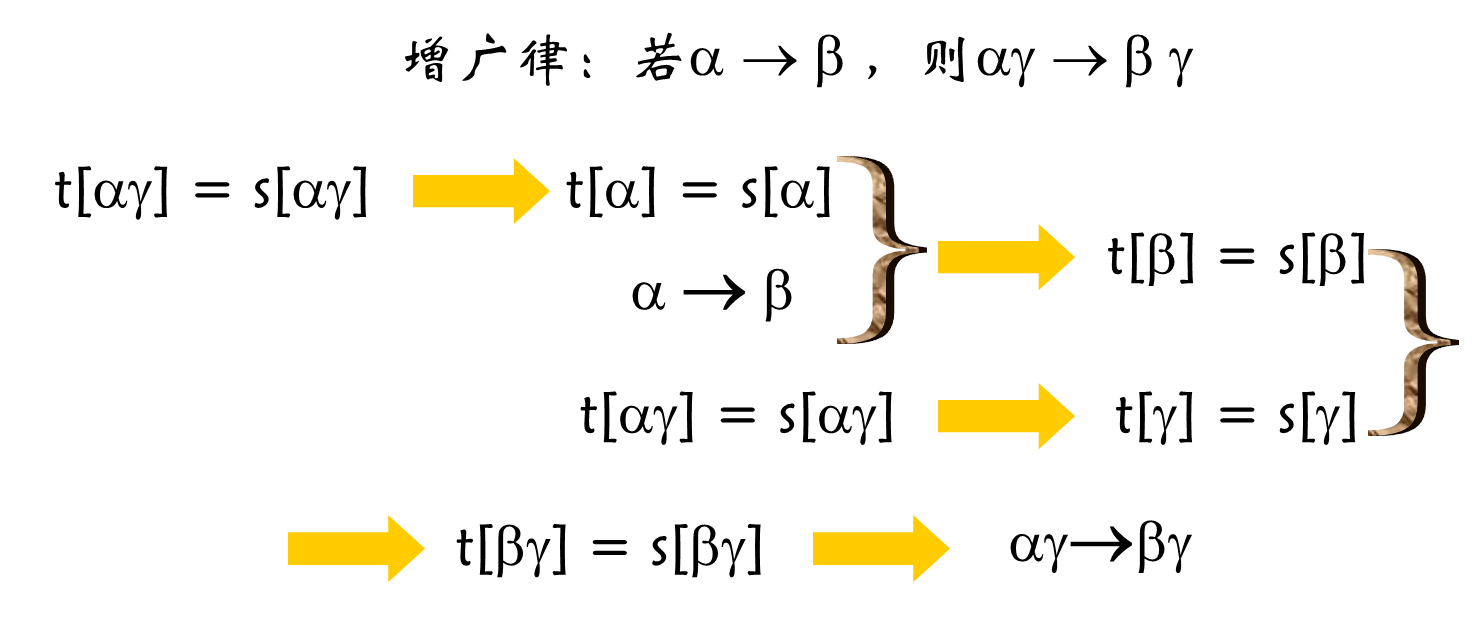
2、增广律的正确性:
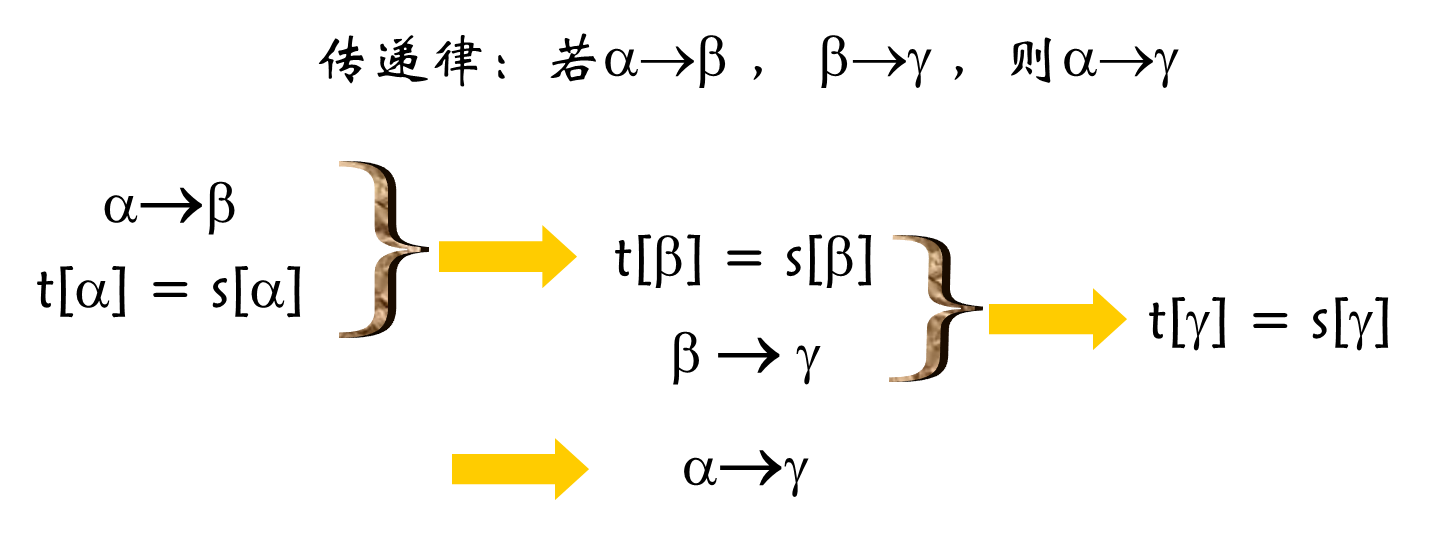
3、传递律的正确性:
完备性(不考、较难):
推论:
证明(这里只给出伪传递律的证明):
求解F闭包算法

这个算法没有太多实际用途,因为求解F的闭包是NP问题
求解属性集闭包算法

重要算法!!
作用:判断属性集a是不是超码
两层循环:外层while循环针对result,内层针对每一个函数依赖
正确性证明:
完备性证明:
==>证明result中有属性集a的全部属性(属性集a的闭包)
属性集a的闭包:由a通过F的函数依赖能推导出的所有属性
假设result中没有a的闭包,也就是说存在一个属性r在a闭包中但是不在result中。即存在一个属性r,能通过函数依赖b->r(b⊆result)推导出来,但是不在result中。但是显然在算法结束的最后一轮,所有的函数依赖能推导出来的r都处理了一遍,result没有增加,所以肯定不存在这样的属性r。因此,假设不成立
练习题:


属性集闭包的作用
1、判断属性集是否为超码
2、通过检验 β ⊆ α+是否成立,可以验证函数依赖α -> β是否成立
候选码求解理论和算法
对于给定的关系模式R(U,F),可将其属性分为4类:
- L类:仅出现在F的函数依赖左部的属性
- R类:仅出现在F的函数依赖右部的属性
- N类:在F的函数依赖两边均未出现的属性
- LR类:在F的函数依赖两边均出现的属性
候选码求解理论
定理一:
对于给定的关系模式R(U,F) ,若a(a⊆U)是L类属性,则a必为R的任意一个候选码的成员。
定理二:
对于给定的关系模式R(U,F) ,若a(a⊆U)是R类属性,则a不包含在R(U,F)任何候选码中
定理三:
对于给定的关系模式R(U,F) ,若a(a⊆U)是N类属性,则a必包含在R(U,F)的任意一个候选码中
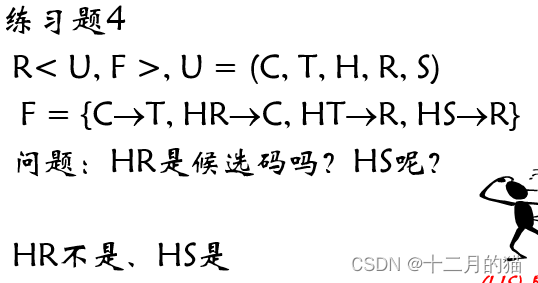
练习题:

无关属性
定义:如果去除一个函数依赖中的属性,不会改变该函数依赖集的闭包,则称该属性是无关的(extraneous)
无关属性在函数依赖左边:

无关属性在函数依赖右边:

关键点:
1、左边简化影响正确性——>F逻辑蕴含来保证正确性
2、右边简化影响完备性——>简化对象逻辑蕴含F保证完备性
检验方法

实际使用中判断无关属性的技巧:
1、左边的无关属性用冗余视角——1、一个就可以判断了,不需要两个属性去决定另外的属性;2、左边的属性存在相互决定的关系,没必要一起存在;3、尽量剩下有用的属性,用检测方法去判断
2、右边的无关属性用冗余视角——其他的/组合的函数依赖已经蕴含这个函数依赖,因此不需要再在右边写这个无关属性
3、无关属性只会出现在大于等于两个的属性处
注意:传递关系是有存在必要的,不是无关属性
正则覆盖
定义:

正则覆盖特点:
1、左半部分唯一
2、没有无关属性
算法:

举例:






关系模式的设计
关系模式存在的问题
关系模式由于数据依赖会产生许多的问题,而消除数据依赖就需要模式分解
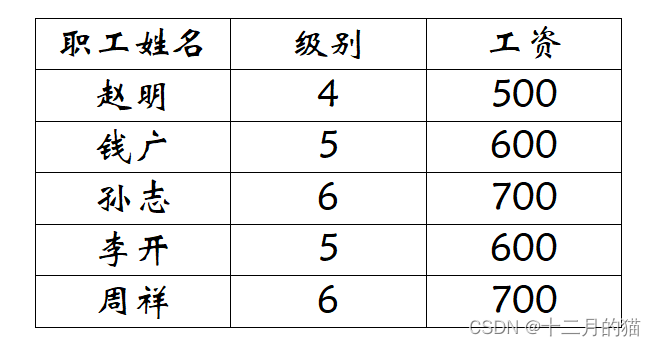
上图存在一个传递依赖:职工姓名——>级别——>工资,因此不是3NF。因此存在信息不可表示问题(插入异常、删除异常)、信息冗余问题(更新异常、数据冗余)
模式分解
定义:

关键点:
1、把属性分解成U1、U2、U3等
2、根据属性在F+中找对应的函数依赖 F1、F2等
3、将Un、Fn组合成Rn
模式分解存在的问题:
1、连接有损性
2、函数依赖有损性
连接有损性:
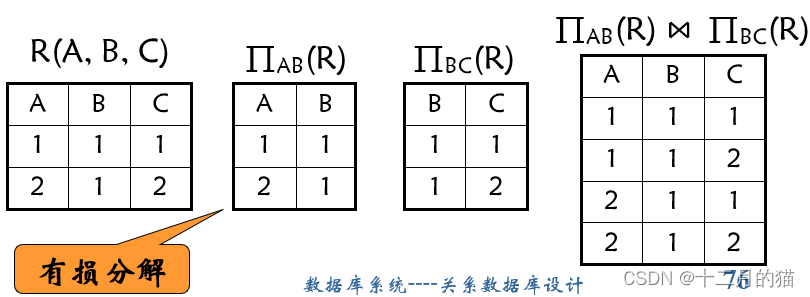
产生原关系模式中没有的关系实例
函数依赖有损性:

不含有原本关系中的函数依赖
判断无损连接分解:
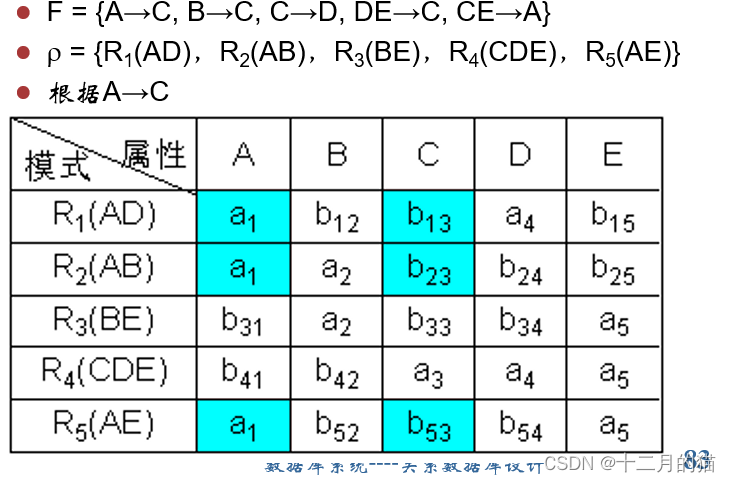
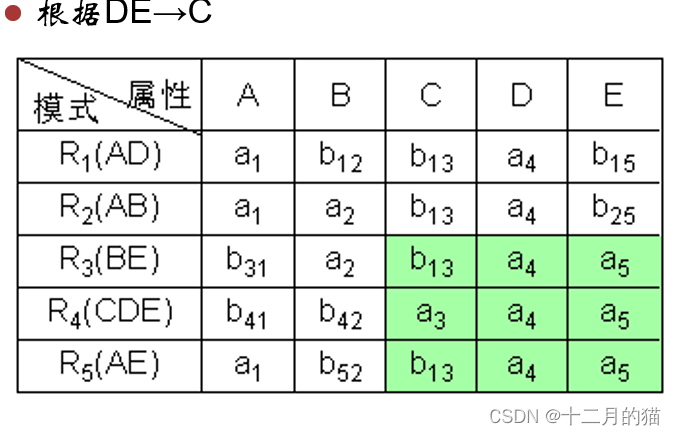
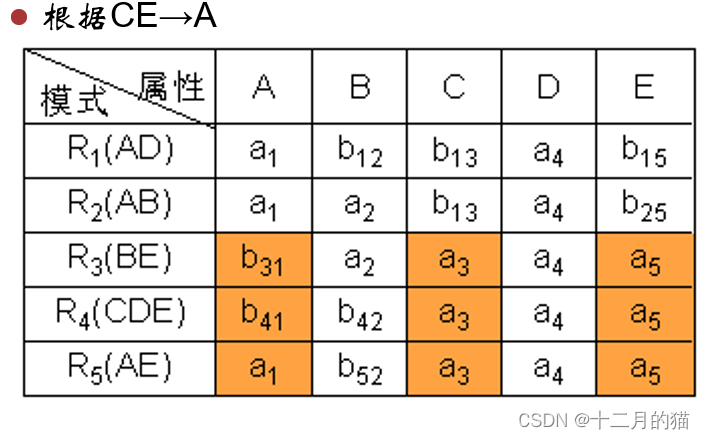
方法一:表格法
初始化:构造一张k行n列的表格,每列对应一个属性Aj(1≤j≤n),每行对应一个模式Ri(1≤i≤k)。如果Aj在Ri中,那么在表格的第i行第j列处填上符号aj,否则填上符号bij。
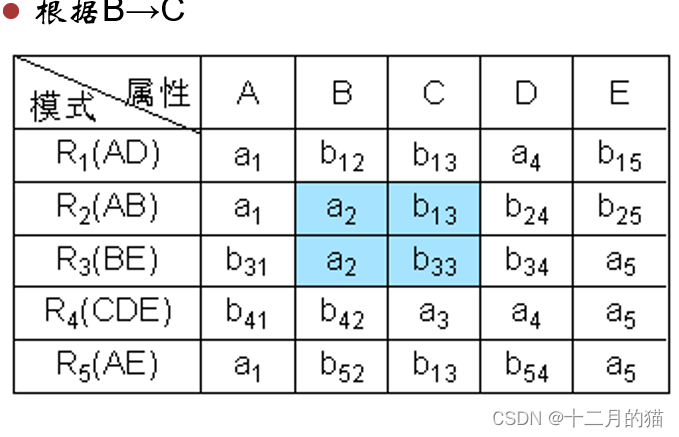
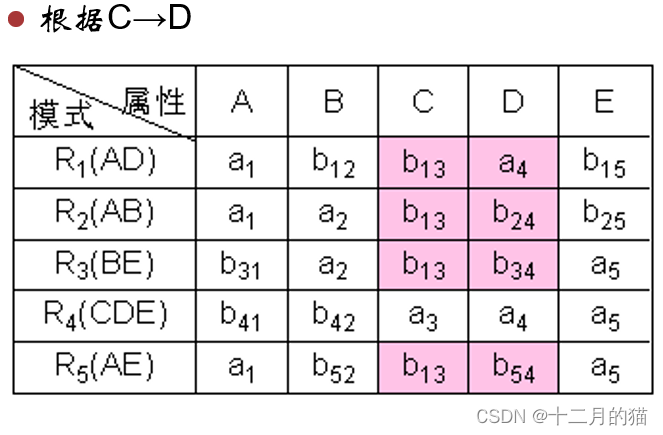
算法过程:对于F中函数依赖:a->b ,如果表格中有多行在a分量上相等,在b分量上不相等,那么把这些行在b分量上改成相等。如果b的分量中有一个是aj,那么另一个也改成aj;如果没有aj,那么用其中的一个bij替换另一个(尽量把ij改成较小的数,亦即取i值较小的那个)
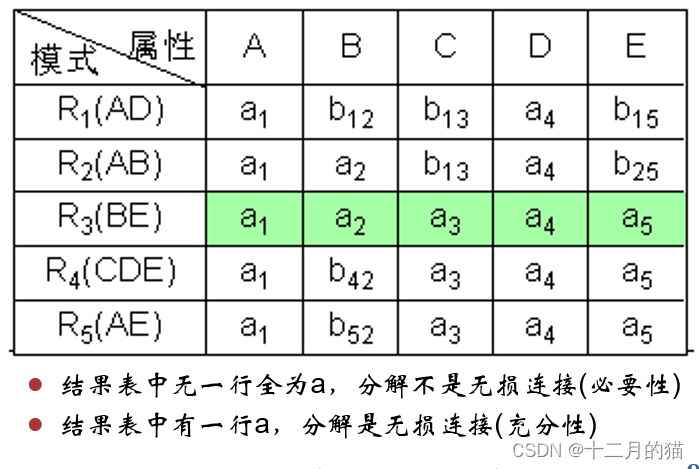
算法终止: 若在修改的过程中,发现表格中有一行全是a,即a1,a2,…,an,那么可立即断定分解r相对于F是无损连接分解,此时不必再继续修改。若经过多次修改直到表格不能修改时,发现表格中不存在有一行全是a的情况,那么分解就是有损的。
算法修改是好几轮循环进行的,不是只进行一轮
表格法流程图:
方法二:快速法
方法理论:
关系模式R(U,F)的分解r={R1,R2},则r是一个无损连接分解的充分条件是:
R1∩R2—>R1或R1∩R2—>R2 成立
R1∩R2—>R1 - R2或R1∩R2—>R2 - R1
举例:

判断保持依赖算法:
方法一:

思想:判断模式分解后的函数依赖并集F‘,求其依赖闭包F’+,判断F‘+是否=F+。来判断分解前后的函数依赖是否相同
问题:上面的方法需要计算F的闭包,也就是函数依赖的闭包。计算这个闭包是NP问题 ,所以这个算法是没有实际用处的
方法二:
方法一的问题就在于需要计算F函数依赖的闭包,这个问题是NP问题。但是我们知道如下性质
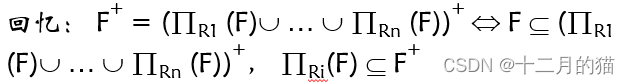
因此可以转为计算分解依赖的闭包,分解依赖的闭包的计算是可解的
如果分解前后的函数依赖完全相同,那么肯定满足保持函数依赖;否则,再看闭包是否满足
方法三:(算法)(手动算时用)
既然不能一次性通过F+的形式去判断是否保持函数依赖,那么我们就把F中的函数依赖一个个拿出来,在分解后的模式中去判断是否存在(把问题通过分解来降低复杂度)

通过把问题分解为多个小问题,从而将问题转化为求解属性闭包的问题,问题就可解了
课堂小练习:
题目一:


题目二:


题目三:

题目四:

前面的铺垫终于全部结束了,接下去,我们可以进入范式的学习!!!!!
别说大家累了,我真的也写累了,www

范式
前面我们分析了造成数据库设计质量高低差距的原因就是——数据依赖。
1、范式就是对关系模式的不同数据依赖程度的要求
2、通过模式分解将一个低级范式转换为若干个高级范式的过程称作规范化
3、 范式是衡量关系模式的标准

第一范式
定义:一个关系模式R所有属性域都是原子的,则称这个关系模式R是第一范式
原子域:域元素被认为是不可分的单元,则称域是原子的
可分性判断:没有明确的是否可分条件,而是要根据业务需求
| 学号 | 费用 | |||
| 书费 | 住宿费 | 学费 | 合计 | |
| s1 | 100 | 1200 | 8000 | 9300 |
| s2 | 125 | 1000 | 5000 | 6125 |
| s3 | 200 | 1500 | 5000 | 6700 |
(上图就是一个不符合第一范式的典型)
改造:将可分属性直接分为单一属性
第二范式
定义:若关系模式R∈1NF,并且每个非主属性都完全函数依赖于R的候选码,则R∈2NF
满足第二范式的属性:1、是主属性(候选码上的属性);2、是非主属性但是没有部分依赖于候选码
改造:将依赖不同主属性的非主属性分为不同的组
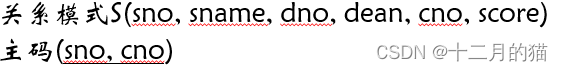
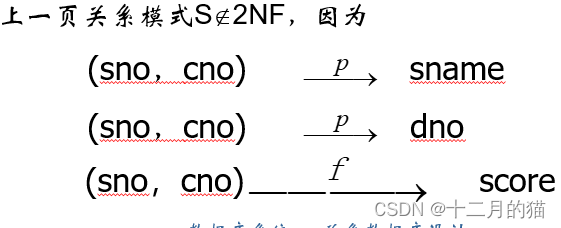
(上图为不符合2NF的典型例子)
第三范式
定义:若关系模式R∈2NF,并且非主属性没有对码的传递依赖,则R∈3NF
改造:将传递依赖的后面一个函数依赖分成另外一组关系模式
改造算法:
1、保持函数依赖3NF分解算法

总结:
- 找出正则覆盖
- 根据正则覆盖中的函数依赖将R分解(一个函数依赖分成一个关系模式R‘)
- 为每一个R’根据函数依赖分配U
例如:

分析这个算法:
1、分组一定是3NF。因为一个函数依赖在一组,所以一定不存在传递依赖
2、因为所有Fc中的函数依赖都在分组中,所以必然保持函数依赖
3、模式分解可能存在两个问题:连接有损性、不保持依赖。本分解算法便不一定是无损的
因此,算法必须要改进:能达到3NF、保持所有函数依赖、连接无损性
思考如何实现连接无损性:
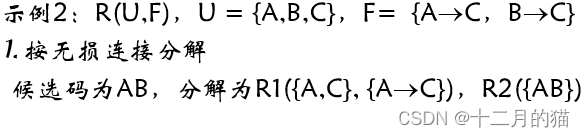
大家来思考一下上面这个分解为什么就是无损的?

关键点在于:R2({AB})
一旦我们加入了包含主码的分解,那么做自然连接后,所得结果关系实例一定和原本的关系实例一样多(因为主码决定R2的关系实例数就是原本R的个数,且主码可以决定一个关系实例)
2、3NF合成算法

总结:
- 前两步思路和前面算法相同
- 若其中一个U中有a则算法结束;否则,增加一个t,让t中的a为候选码,从而保证无损分解
正则覆盖不唯一,因此3NF合成算法结果不唯一
练习题

BCNF
定义:

无论是主属性还是非主属性,只要不是平凡依赖,左边都是完全依赖候选码
判断BCNF算法:
分解前:

分解后:

模式分解会导致部分F+中的函数依赖丢失,因此分解后BCNF的判断需要考虑F+中的关系;
关系模式分解算法——BCNF:

核心思想:将不满足BCNF的关系模式分解为满足BCNF的多个子关系模式
结束条件:检查一轮关系模式Ri都满足就退出while循环
修改条件:非平凡依赖;a∩b=空集;a不是超码
练习题

不要求数据库设计一定要达到BCNF,这有时会导致函数依赖的缺失
函数依赖综合练习题

这里不给出答案,仅仅给大家参考有哪些能考试的重点知识点:
1、属性闭包算法
2、判断候选码(候选码四种形式)
3、正则覆盖(合成、去无关)算法
4、3NF合成算法(正则覆盖+候选码无损保证)
5、BCNF无损连接分解法(找不符合的关系模式,将其分解为符合的)
总结
本文的所有知识点、图片均来自《数据库系统概念》(黑宝书)、山东大学李晖老师PPT。不可用于商业用途转发。
本篇已经码了七个多小时(这篇确实难度很大wwww)
属于是高级数据库设计,但是还是很值的大家学习的!!!
只有规范化数据库的设计,减少了数据依赖,数据库的插入、删除、更新、冗余等异常/问题才能解决。这将让我们的数据库设计水平远高于E-R模型设计
如果能帮助到大家,大家可以点点赞、收收藏呀~
















![[Mdfs] lc3067. 在带权树网络中统计可连接服务器对数目(邻接表+图操作基础+技巧+好题)](https://img-blog.csdnimg.cn/direct/fde198b18881419a8e203007e647bb0c.png)