LeetCode:48. 旋转图像

受到力扣hot100:54. 螺旋矩阵的启发,我们可以对旋转图像按层旋转,我们只需要记录四个顶点,并且本题是一个方阵,四个顶点就能完成图像的旋转操作。
1、逐层旋转
注意到,一层的四个顶点存在一定的位置关系,我们只需要记录四个值:
top_row、bottom_row、left_col、right_col,则上右下左四个顶点分别为:
(top_row,left_col)、(top_row,right_col)、(bottom_row,right_col)、(bottom_row,left_col)
当我们需要更新层时,注意矩阵的下标,只需进行如下操作:
top_row++bottom_row--left_col++right_col--
这样我们就找到了一层的四个顶点,以及更新层的操作。
现在我们只需要逐层更新即可。
时间复杂度: O ( n 2 ) O(n^2) O(n2)
空间复杂度: O ( 1 ) O(1) O(1)
class Solution {
public:void rotate(vector<vector<int>>& matrix) {int top_row = 0, left_col = 0;int bottom_row = matrix.size() - 1, right_col = matrix.size() - 1;//由于size() > 1,所以可以这样做while(top_row < bottom_row){//方阵,结束条件int step = right_col - left_col;for(int i = 0; i < step; ++ i){int temp;//上换到右temp = matrix[top_row + i][right_col];matrix[top_row + i][right_col] = matrix[top_row][left_col + i];//右换到下int temp2 = temp;temp = matrix[bottom_row][right_col - i];matrix[bottom_row][right_col - i] = temp2;//下换到左temp2 = temp;temp = matrix[bottom_row - i][left_col];matrix[bottom_row - i][left_col] = temp2;//左换到上matrix[top_row][left_col + i] = temp;}//更新层top_row++;bottom_row--;left_col++;right_col--;}return ;}
};
- 我们需要注意一个问题,判断结束条件时,由于方阵行数是
n可以是偶数也可以是奇数,奇数时,上行和下行相等则结束。但如果是偶数时,他俩会交叉,因此是下行大于上行时结束!- 为了在编程时忽略奇偶数的这个问题,我们可以编程时将判断条件更宽泛
- 如果
top_row > bottom_row也不满足条件,那不要写top_row == bottom_row,而是将两者结合起来写,这样可以避免自己的遗漏。
为了节省临时变量,我们也可以按左下转到左上,右下转到左下,右上转到右下,左上转到右上的顺序旋转,这样只需要存储左上的值即可。
class Solution {
public:void rotate(vector<vector<int>>& matrix) {int top_row = 0, left_col = 0;int bottom_row = matrix.size() - 1, right_col = matrix.size() - 1;//由于size() > 1,所以可以这样做while(top_row < bottom_row){//方阵,结束条件int step = right_col - left_col;for(int i = 0; i < step; ++ i){int temp = matrix[top_row][left_col + i];matrix[top_row][left_col + i] = matrix[bottom_row - i][left_col];左换到上matrix[bottom_row - i][left_col] = matrix[bottom_row][right_col - i];//下换到左matrix[bottom_row][right_col - i] = matrix[top_row + i][right_col];//右换到下matrix[top_row + i][right_col] = temp;//上换到右}//更新层top_row++;bottom_row--;left_col++;right_col--;}return ;}
};
和官解的方法二类似。
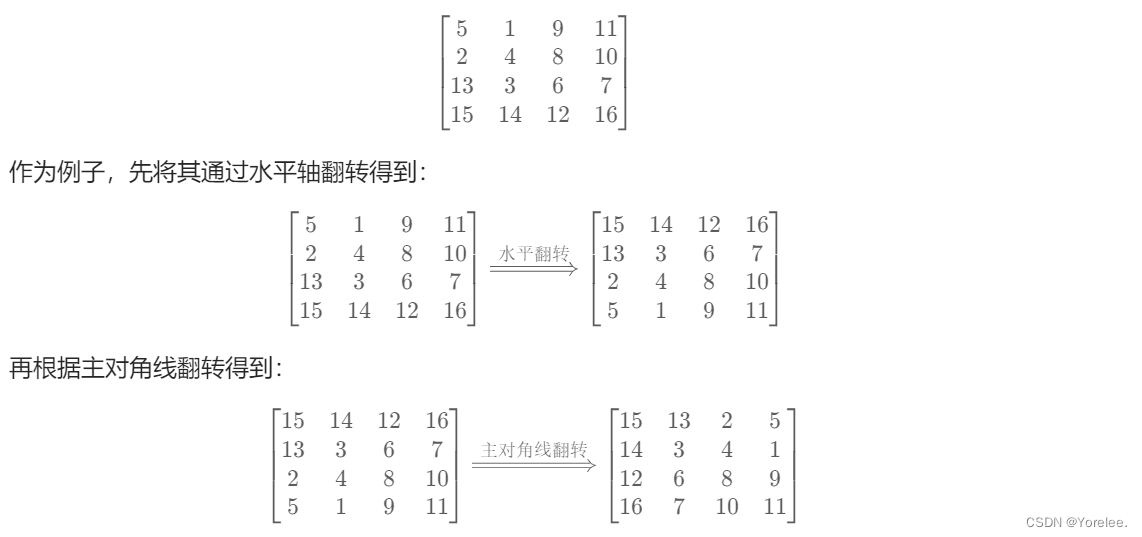
2、两次翻转等于旋转
class Solution {
public:void rotate(vector<vector<int>>& matrix) {int n = matrix.size();// 水平翻转for (int i = 0; i < n / 2; ++i) {for (int j = 0; j < n; ++j) {swap(matrix[i][j], matrix[n - i - 1][j]);}}// 主对角线翻转for (int i = 0; i < n; ++i) {for (int j = 0; j < i; ++j) {swap(matrix[i][j], matrix[j][i]);}}}
};