LogicFlow 实例
创建实例
每一个流程设计界面,就是一个 LogicFlow 的实例。
<template><div id="container"></div><!-- 用于显示 LogicFlow 图表的容器 -->
</template>
<script>// 创建 LogicFlow 实例const lf = new LogicFlow({container: document.getElementById('container')!, // 指定容器元素grid: true // 启用网格})
</script>
当创建一个实例的时候,我们需要传递初始化LogicFlow实例的配置项。LogicFlow支持非常丰富的初始化配置项,但是只有LogicFlow画布初始化时挂载的DOM节点container参数是必填的。完整的配置项参见LogicFlow API
图数据
在 LogicFlow 里面,我们把流程图看做是由节点和连线组成的图。所以我们采用如下数据结构来表示 LogicFlow 的图数据。
// 定义图形编辑器的初始数据
const data = {// 节点数组nodes: [{id: 'node_id_1', // 节点标识type: 'rect', // 节点形状类型:矩形x: 100, // 节点在画布上的 x 坐标y: 100, // 节点在画布上的 y 坐标text: { x: 100, y: 100, value: '节点1' }, // 节点的文本及其位置properties: {} // 节点的自定义属性},{id: 'node_id_2', // 另一个节点标识type: 'circle', // 节点形状类型:圆形x: 200, // 节点在画布上的 x 坐标y: 300, // 节点在画布上的 y 坐标text: { x: 300, y: 300, value: '节点2' }, // 节点的文本及其位置properties: {} // 节点的自定义属性}],// 边数组edges: [{id: 'edge_id', // 边的标识type: 'polyline', // 边的类型:多段线sourceNodeId: 'node_id_1', // 起始节点targetNodeId: 'node_id_2', // 目标节点text: { x: 139, y: 200, value: '连线' }, // 边上的文本及其位置startPoint: { x: 100, y: 140 }, // 起始点坐标endPoint: { x: 200, y: 250 }, // 结束点坐标pointsList: [{ x: 100, y: 140 },{ x: 100, y: 200 },{ x: 200, y: 200 },{ x: 200, y: 250 }], // 折点的列表,定义折线的形状properties: {} // 边的自定义属性}]
}
-
text可以直接使用字符串,这个时候,如果是节点的文本,LogicFlow 会自动采用节点坐标作为节点文本坐标,如果是连接文本,LogicFlow 会基于不同的连线类型计算一个合适的坐标作为节点坐标。在有些应用场景下,我们文本是可以拖动的,为了保持一致,LogicFlow导出的文本数据都会带上坐标。 -
目前,在 LogicFlow 内部内置了
line,polyline,bezier三种基础连线,这三种连线都有startPoint、endPoint数据。但是其中line导出的数据是不会带上pointsList。对于polyLine,pointsList表示折线所有的点。对于bezier,pointsList表示['起点', '第一个控制点', '第二个控制点', '终点']。效果如下所示:
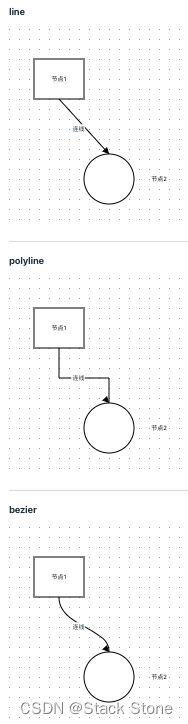
代码:Example04.vue -
properties是LogicFlow保留给具体业务场景使用的数据。例如:在审批流场景,我们定义某个节点,这个节点通过了,节点为绿色,不通过节点为红色。那么节点的数据描述可以为:{type: 'apply',properties: {isPass: true} } -
type表示节点或者连线的类型,这里的类型不仅可以是rect,polyline这种 LogicFlow 内置的基础类型,也可以是用户基于基础类型自定义的类型。如:
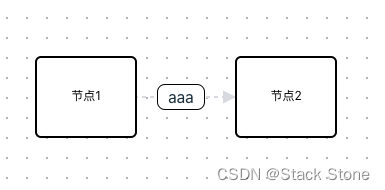
代码:Example03
图渲染
数据直接放入render方法中执行就可以渲染出图了。
lf.render(graphData)
上一篇:初步使用 LogicFlow
下一篇:LogicFlow 基础 节点 Node











![[Qt的学习日常]--常用控件3](https://img-blog.csdnimg.cn/direct/ea9bc34104da484dbfc5cc28f22be9db.png)
