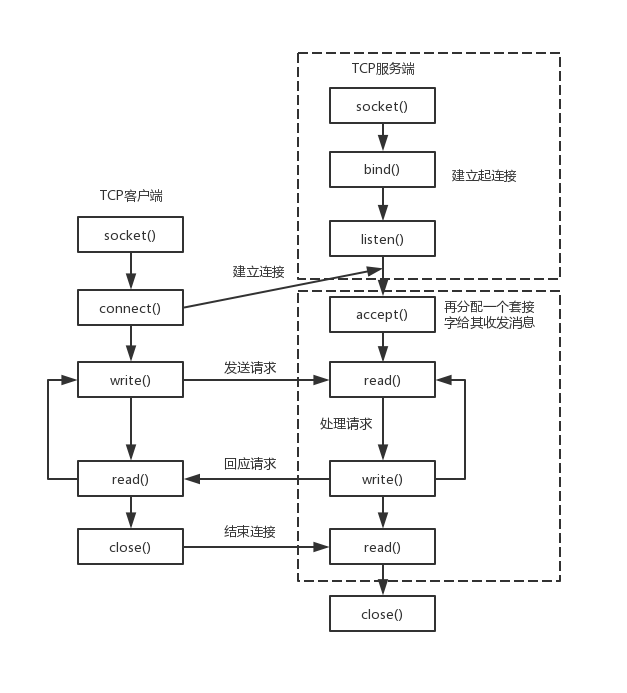
商用密码算法种类

商用密码算法
密码学概念、协议与算法之间的依赖关系
数字签名、证书-公钥密码、散列类算法
消息验证码-对称密码 ,散列类
安全目标与算法之间的关系
机密性--对称密码、公钥密码
完整性--散列类算法
可用性--散列类、公钥密码
真实性--公钥密码
不可否认--公钥密码
SM2椭圆曲线公钥加密
公钥密码体制
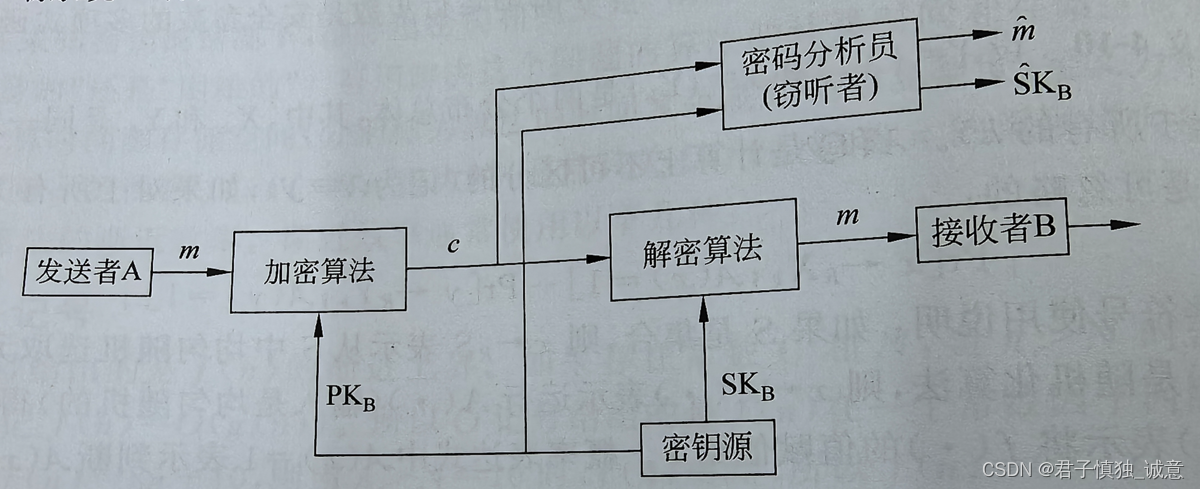
公钥体制加密
- 接收者B产生一对密钥:私钥--
,公钥--
- A想向B发消息m,则使用B的公钥加密m,表示为
, c是加密后的密文,
是加密算法
- B收到密文c后,用自己的私钥
解密,表示为
,D是解密算法
只能由B进行解密
公钥体制认证
用户A用自己的私钥对m进行加密,,将c发给B,B用A的公钥解密
从m得到c的过程是经过A的私钥加密的,只能A才能做到,因此c可以当作A对m的数字签名。

双重加密、解密
为了同时具有保密功能和认证功能,可以使用双重加、解密
发送方先用自己的私钥对消息加密,用于提供数字签名。再用接收方的公钥加密,表示为
接收者收到后,x先用自己的私钥,再用发送方的公钥进行两次解密,解密过程为

椭圆曲线密码体制
椭圆曲线密码 Elliptic CurveCryptography ECC:利用椭圆曲线实现密码技术
椭圆曲线上的离散对数问题
本质:已知xG求数x的问题
椭圆曲线密码中,先确定一条椭圆曲线,然后对椭圆曲线上的某一些点之间的“运算”进行定义,利用这些“运算”来进行密码技术相关的计算。
已知
椭圆曲线E
椭圆曲线E上的一点G(基点)
椭圆曲线上的一点xG(G的x倍)
求解
数x
椭圆曲线Diffie-Hellman密钥交换
AB需要共享一个对称密码的密钥,用椭圆曲线Diffie-Hellman密钥交换,生成共享密钥
- A向B发送点G。G被窃听无影响
- A生成随机数a,将a作为A的私钥
- B生成随机数b,将b最为B的私钥
- A向B发送点aG
- B向A发送bG
- A对收到的bG计算其在椭圆曲线上a倍的点,a(bG)=abG==共享密钥
- B对收到的aG计算其在椭圆曲线上b倍的点,b(aG)=baG=abG==共享密钥
每次通信使用不同的随机数,共享密钥也会随之改变==保证了前向安全性forward secrecy
SM2
SM2是国家密码管理局颁布的中国商用公钥密码标准算法,是一组椭圆曲线密码算法,包含加解密算法、数字签名算法。
SM2与国际ECC比较
ECC算法采用国际机构建议的曲线和参数,SM2算法的参数需要利用一定的算法产生,算法中加入了用户特异性的曲线参数、基点、用户的公钥点信息,安全性更高
ECC中,用户可以选择MD5或SHA-1等国际通用的哈希算法,SM2使用SM3哈希算法,SM3哈希算法输出为256比特,与SHA-256算法安全性相当
SM2椭圆曲线公钥密码加密算法
基本参数
基于素数域的SM2算法参数如下:
的特征p为m比特长的素数,p要尽可能大;
长度不小于192比特的比特串SEED;
上的2个元素a,b,满足
,定义曲线
基点;
G的阶n为m比特长的素数,满足;
余因子,其中
是曲线
的点数。
SEED,a,b产生的算法:
- 任意选取长度不小于192比特的比特串SEED;
- 计算
,记
,其中
表示256比特输出的SM3哈希算法
- 取
;
- 取
;
- 在
上任意选择2个元素a,b,满足
;
- 若
,则返回1;
- 所选择的
上的曲线是
- 输出(SEED,a,b)
密钥产生
假设接收方为B,B的秘密钥取{1,2,...,n-1}中的一个随机数,记为
,其中G的阶n
B的公开钥取为椭圆曲线上的点:,其中,
是基点
加密算法
假设发送方是A,A要发送的消息表示为M比特串,M的长度为klen.算法如下:
- 选择随机数
- 计算椭圆曲线点
,将x1,y1表示为比特串;
- 计算椭圆曲线点
,若S为无穷远点,则报错退出;
- 计算椭圆曲线
,将x2,y2表示为比特串;
- 计算
,若t为全0的比特串,则返回1;
- 计算
----(mod 2 加法)
- 计算
- 输出密文C=(C1,C2,C3)
KDF(*)是密钥派生函数,本质为一个伪随机数产生函数,用来产生密钥,这里KDF为SM3,第(3)步的H也是SM3
解密算法
B收到密文C后,进行解密,过程如下:
- 从C中取出C1,将C1表示为椭圆曲线上的点,验证C1是否满足椭圆曲线方程。不满足就报错退出;
- 计算椭圆曲线点
,若S为无穷远点,则报错退出;
- 计算
,将x2,y2表示为比特串;
- 计算
,若t为全0的比特串,则报错退出;
- 从C中取出C2,计算
;
- 计算
,从C中取出C3,若
则报错退出;
- 输出明文
SM2椭圆曲线公钥密码签名算法
基本参数
与前面加密算法的参数设置相同
密钥产生
与与前面加密算法产生方法一样,记为
设是A的长度为
比特的标识,
由
转换而成的两个字节,A计算
,其中a,b是椭圆曲线方程的参数,
是基点G的坐标,
是
的坐标。将这些值转换为比特串后,在进行
。验证方B验证签名时,也需要计算
签名算法
设待签名的消息为M,操作如下:
- 取
- 计算
,将e转换为整数,Hv是输出为v比特长的哈希函数
- 用随机数产生器生成随机数
- 计算椭圆曲线点
;
- 计算
,若r=0或者r+k=n,则返回3
- 计算
,若s=0,则返回3
- 消息M的签名为(r,s)
验证算法
B收到消息以及其签名
,进行验证操作:
检验是否成立,若不成立,验证失败;
检验是否成立,若不成立,验证失败;
置
计算,并将其转换为整数;
计算,若t=0,验证失败
计算椭圆曲线点
计算,检查
是否成立,若成立则验证通过,否则,验证失败