---

🌈个人主页: 鑫宝Code
🔥热门专栏: 闲话杂谈｜ 炫酷HTML | JavaScript基础
​💫个人格言: "如无必要，勿增实体"

---

Lasso回归：稀疏建模与特征选择的艺术

引言

在高维数据的海洋中，如何有效识别并利用关键特征成为数据分析和机器学习中的重要挑战。Lasso回归（Least Absolute Shrinkage and Selection Operator），作为一种引入了L1正则化的线性模型，不仅能够实现特征的自动选择，还能有效处理多重共线性问题，为复杂数据分析提供了强有力的工具。本文将深入探讨Lasso回归的理论基础、算法实现、优势特点及其在实际应用中的策略和技巧，旨在为读者提供一个全面而深入的理解。

一、Lasso回归简介

1.1 基本概念

Lasso回归由Robert Tibshirani于1996年提出，是线性回归的一种正则化形式。它在标准线性回归损失函数的基础上，加入了L1范数惩罚项，旨在约束模型参数的绝对值大小，从而促使某些参数直接被“压缩”至零，实现特征的选择性稀疏化。

1.2 数学表达式

Lasso回归的目标函数可表述为：
$$\underset{{\beta }_0,\beta }{\min }\left(\frac{1}{2n}\sum _{i=1}^n(y_i-({\beta }_0+{\beta }_1{x}_{i1}+...+{\beta }_p{x}_{ip}){)}^2+\lambda \sum _{j=1}^p|{\beta }_j|\right)$$
其中，第一部分是标准的平方损失函数，用于衡量模型预测值与真实值之间的差距；第二部分是L1正则化项，$\lambda$是正则化强度参数，控制正则化的强度。

二、算法与实现

2.1 解决方案

Lasso回归的求解通常不具有闭式解，常见的求解方法包括：

• 坐标下降法（Coordinate Descent）：逐个更新每个参数，直到收敛。
  

• 最小角回归（LARS, Least Angle Regression）：一种迭代算法，能同时处理Lasso和Ridge回归问题。
  

• 梯度下降法配合软阈值操作也可以实现Lasso回归的求解。
  

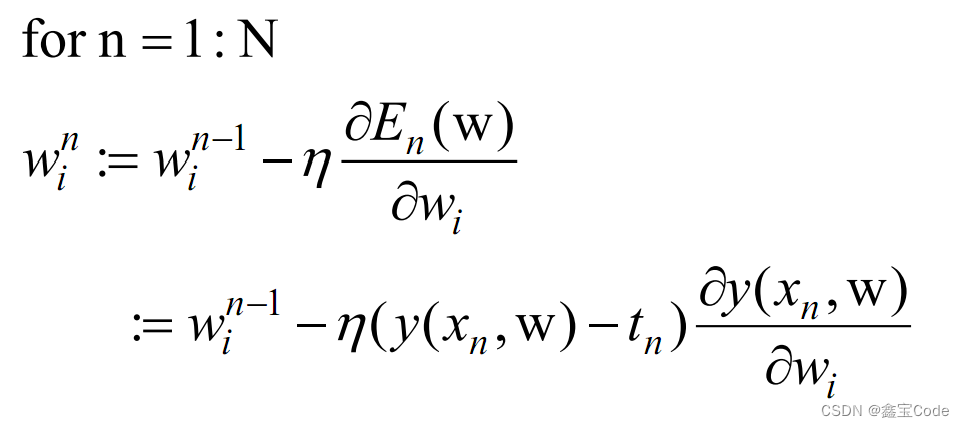
2.2 Python实现示例

使用scikit-learn库中的Lasso类可以轻松实现Lasso回归：

from sklearn.linear_model import Lasso
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split# 生成模拟数据
X, y = make_regression(n_samples=100, n_features=10, noise=0.1)# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 初始化Lasso回归模型
lasso = Lasso(alpha=0.1)# 训练模型
lasso.fit(X_train, y_train)# 预测
predictions = lasso.predict(X_test)

三、Lasso回归的优势与特性

3.1 特征选择

Lasso回归最显著的优势在于其自然地实现了特征选择。通过强制某些系数为零，模型能够识别出对预测最重要的特征子集，这对于理解和解释模型特别有用，尤其是在高维数据场景下。

3.2 处理多重共线性

Lasso回归对于高度相关的特征具有较好的鲁棒性，能够在一定程度上缓解多重共线性问题，因为L1正则化倾向于选择一个特征而将其他相关特征的系数压低至零。

3.3 收缩效应

即使参数没有被完全压缩至零，Lasso也会对所有参数进行某种程度的“收缩”，这有助于防止过拟合，提高模型的泛化能力。

四、超参数调整与模型选择

4.1 $\lambda$的选择

• 交叉验证：是最常用的方法，通过在不同子集上评估模型性能，找到最优的(\lambda)。
• 信息准则（如AIC、BIC）：在某些情况下也可作为选择正则化强度的依据。

4.2 与Ridge回归的对比

虽然Ridge回归也采用正则化，但它使用的是L2范数，倾向于保留所有特征但减小它们的系数。选择Lasso还是Ridge取决于是否需要进行特征选择，以及数据的特性。

五、实际应用策略与注意事项

5.1 数据预处理

• 标准化/归一化：Lasso回归对特征尺度敏感，预处理是必要的。
• 缺失值处理：应合理填充或删除含有大量缺失值的特征。

5.2 解释与可解释性

Lasso回归模型的稀疏性使其更易于解释，但需要注意的是，特征选择结果可能依赖于(\lambda)的选择，解释时需谨慎。

5.3 高维数据处理

在极高维度的情况下，Lasso可能遇到计算挑战，考虑使用迭代算法或分布式计算资源。

六、结论与展望

Lasso回归以其独特的特征选择能力和对多重共线性的良好处理，在众多领域展现出广泛的应用价值。随着计算技术的进步和数据科学的深入发展，Lasso回归及其变体（如Elastic Net回归）将持续优化，为复杂数据分析和决策支持提供更为强大的工具。对于研究人员和实践者来说，深入理解Lasso回归的工作原理及其在特定情境下的适用性和限制，将是提升数据挖掘和预测能力的关键。