切线
要求与曲线 C C C相切于 P ( a , f ( a ) ) P(a, f(a)) P(a,f(a))点的切线,我们可以在曲线上找到与之相近的一点 Q ( x , f ( x ) ) Q(x, f(x)) Q(x,f(x)),然后求出割线 P Q PQ PQ的斜率:
m P Q = f ( x ) − f ( a ) x − a m_{PQ} = \frac{f(x) - f(a)}{x - a} mPQ=x−af(x)−f(a)
当 Q Q Q沿着曲线向 P P P逐渐靠近, m P Q m_{PQ} mPQ会越来越接近切线的斜率 m m m。
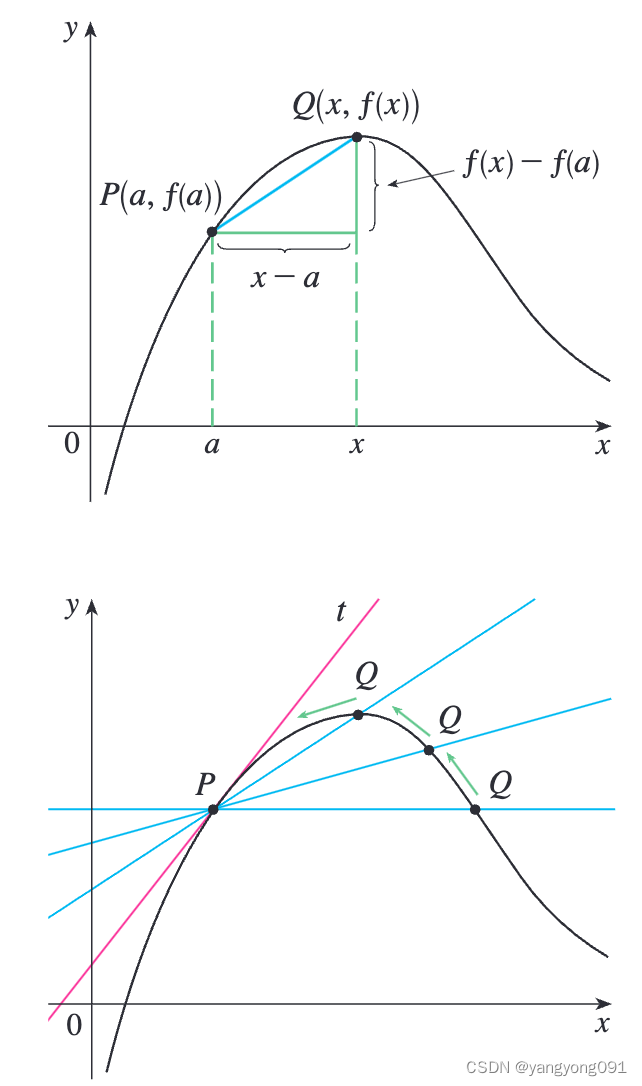
定义 1:与曲线 f ( x ) f(x) f(x)切于点 P ( a , f ( a ) ) P(a, f(a)) P(a,f(a))的切线是一条穿过 P P P的直线,其斜率为:
m = lim x → a f ( x ) − f ( a ) x − a m = \lim_{x \to a} \frac{f(x) - f(a)}{x - a} m=x→alimx−af(x)−f(a)
例一
求抛物线 y = x 2 y = x^2 y=x2在点 P ( 1 , 1 ) P(1, 1) P(1,1)的切线公式。
解:
已知 a = 1 a = 1 a=1和 f ( x ) = x 2 f(x) = x^2 f(x)=x2,因此切线的斜率为:
m = lim x → 1 f ( x ) − f ( 1 ) x − 1 = lim x → 1 x 2 − 1 x − 1 = lim x → 1 ( x − 1 ) ( x + 1 ) x − 1 = lim x → 1 ( x + 1 ) = 1 + 1 = 2 \begin{align*} m &= \lim_{x \to 1} \frac{f(x) - f(1)}{x - 1} \\ &= \lim_{x \to 1} \frac{x^2 - 1}{x - 1} \\ &= \lim_{x \to 1} \frac{(x - 1)(x + 1)}{x - 1} \\ &= \lim_{x \to 1} (x + 1) \\ &= 1 + 1 = 2 \end{align*} m=x→1limx−1f(x)−f(1)=x→1limx−1x2−1=x→1limx−1(x−1)(x+1)=x→1lim(x+1)=1+1=2
再使用切点式,有
y − 1 = 2 ( x − 1 ) y = 2 x − 1 \begin{align*} y - 1 &= 2(x - 1) \\ y &= 2x - 1 \end{align*} y−1y=2(x−1)=2x−1
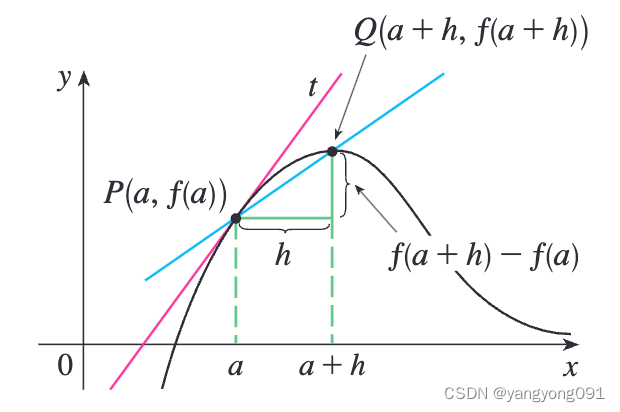
除定义中给出的求切线斜率的表达式之外,还有用下面的表达式 2求切线斜率:
m = lim h → 0 f ( a + h ) − f ( a ) h m = \lim_{{h \to 0}} \frac{{f(a + h) - f(a)}}{h} m=h→0limhf(a+h)−f(a)
例二
求双曲线 y = 3 / x y = 3/x y=3/x在点 ( 3 , 1 ) (3, 1) (3,1)的切线方程。
根据表达式2有
m = lim h → 0 f ( 3 + h ) − f ( 3 ) h = lim h → 0 ( 3 3 + h − 1 h ) = lim h → 0 ( 3 − ( 3 + h ) 3 + h h ) = lim h → 0 ( − h h ( 3 + h ) ) = lim h → 0 ( − 1 3 + h ) = − 1 3 \begin{align*} m &= \lim_{{h \to 0}} \frac{f(3 + h) - f(3)}{h} \\ &= \lim_{{h \to 0}} \left( \frac{\frac{3}{3 + h} - 1}{h} \right) \\ &= \lim_{{h \to 0}} \left( \frac{\frac{3 - (3 + h)}{3 + h}}{h} \right) \\ &= \lim_{{h \to 0}} \left( \frac{-h}{h(3 + h)} \right) \\ &= \lim_{{h \to 0}} \left( \frac{-1}{3 + h} \right) \\ &= -\frac{1}{3} \end{align*} m=h→0limhf(3+h)−f(3)=h→0lim(h3+h3−1)=h→0lim(h3+h3−(3+h))=h→0lim(h(3+h)−h)=h→0lim(3+h−1)=−31
速度
已知路程和时间的关系式 f ( x ) f(x) f(x),可以通过下面的表达式求位置 P P P和 Q Q Q之间移动的平均速度:
f ( a + h ) − f ( a ) h \frac{f(a+h) - f(a)}{h} hf(a+h)−f(a)
现在假设我们计算越来越短的时间间隔 ([a, a+h]) 上的平均速度。换句话说,我们让 (h) 趋近于 0。就像在下落的球的例子中一样,我们定义在时间 (t=a) 时的速度(或瞬时速度)(v(a)) 为这些平均速度的极限:
v ( a ) = lim h → 0 f ( a + h ) − f ( a ) h v(a) = \lim_{h \to 0} \frac{f(a+h) - f(a)}{h} v(a)=h→0limhf(a+h)−f(a)
例三
假设一个球从CN塔上层观景台(距地面450米)掉下。
(a) 球在5秒钟后的速度是多少?
(b) 球撞到地面时的速度是多少?
提示:自由落体运动的公式为 s ( t ) = 1 2 g t 2 s(t) = \frac{1}{2} g t^2 s(t)=21gt2。
导数
导数定义:一个函数 f f f在某个数 a a a处的导数,记作 f ’ ( a ) f’(a) f’(a),定义为:
f ′ ( a ) = lim h → 0 f ( a + h ) − f ( a ) h f{\prime}(a) = \lim_{h \to 0} \frac{f(a+h) - f(a)}{h} f′(a)=h→0limhf(a+h)−f(a)
这个极限,如果存在,就被称为函数 f f f在点 a a a处的导数,它表示函数 f f f在 a a a处的瞬时变化率或斜率。也可以用下面的方程表示:
f ′ ( a ) = lim x → a f ( x ) − f ( a ) x − a f{\prime}(a) = \lim_{x \to a} \frac{f(x) - f(a)}{x - a} f′(a)=x→alimx−af(x)−f(a)
例四
找到函数 f ( x ) = x 2 + 8 x + 19 f(x) = x^2 + 8x + 19 f(x)=x2+8x+19在数 a a a处的导数。
根据切线和导数的定义,我们可以得出一个结论:切线在点 ( a , f ( a ) ) (a, f(a)) (a,f(a))的斜率等于导数 f ′ ( a ) f{\prime}(a) f′(a)。
如果我们使用直线的点斜式方程,我们可以写出曲线 y = f ( x ) y = f(x) y=f(x)在点 ( a , f ( a ) ) (a, f(a)) (a,f(a))处的切线方程: y − f ( a ) = f ′ ( a ) ( x − a ) y - f(a) = f'(a)(x - a) y−f(a)=f′(a)(x−a)
例五
找到抛物线 y = x 2 + 8 x + 19 y = x^2 + 8x + 19 y=x2+8x+19在点 ( 3 , − 6 ) (3, -6) (3,−6)处的切线方程。
变化率
假设 y y y是 x x x的函数,我们写作 y = f ( x ) y = f(x) y=f(x)。如果 x x x从 x 1 x_1 x1变化到 x 2 x_2 x2,那么 x x x的变化量(也称为 x x x的增量)是
Δ x = x 2 − x 1 \Delta x = x_2 - x_1 Δx=x2−x1
相应地 y y y的变化量是
Δ y = f ( x 2 ) − f ( x 1 ) \Delta y = f(x_2) - f(x_1) Δy=f(x2)−f(x1)
商
Δ y Δ x = f ( x 2 ) − f ( x 1 ) x 2 − x 1 \frac{\Delta y}{\Delta x} = \frac{f(x_2) - f(x_1)}{x_2 - x_1} ΔxΔy=x2−x1f(x2)−f(x1)
被称为 y y y相对于 x x x在区间 [ x 1 , x 2 ] [x_1, x_2] [x1,x2]上的平均变化率,可以解释为图中割线 P Q PQ PQ的斜率。
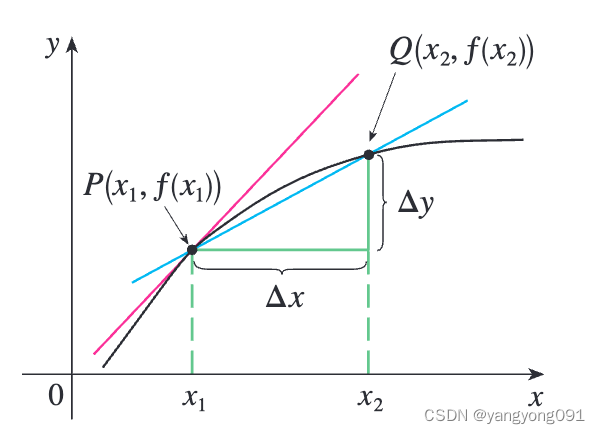
通过与速度类比,我们通过让 x 2 x_2 x2趋近 x 1 x_1 x1,从而让 Δ x \Delta x Δx趋近0,来考虑在越来越小的区间上的平均变化率。这些平均变化率的极限称为 y y y相对于 x x x在 x = x 1 x = x_1 x=x1处的瞬时变化率,它(与速度的情况一样)被解释为曲线 y = f ( x ) y = f(x) y=f(x)在点 P ( x 1 , f ( x 1 ) ) P(x_1, f(x_1)) P(x1,f(x1))处的切线的斜率:
lim Δ x → 0 Δ y Δ x = lim x 2 → x 1 f ( x 2 ) − f ( x 1 ) x 2 − x 1 \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = \lim_{x_2 \to x_1} \frac{f(x_2) - f(x_1)}{x_2 - x_1} Δx→0limΔxΔy=x2→x1limx2−x1f(x2)−f(x1)
前面我们已经知道,导数 f ′ ( a ) f'(a) f′(a)是曲线 y = f ( x ) y = f(x) y=f(x)在 x = a x = a x=a处的切线的斜率。现在我们知道切线的斜率就是瞬时变化率,因此可以说:导数 f ′ ( a ) f'(a) f′(a)是 y = f ( x ) y = f(x) y=f(x)在 x = a x = a x=a处的瞬时变化率。
如果我们绘制曲线 y = f ( x ) y = f(x) y=f(x),那么瞬时变化率就是该曲线在 x = a x = a x=a处的切线的斜率。这意味着,当导数很大时(因此曲线很陡,如图中的点P), y y y值变化很快。当导数很小时,曲线相对平缓(如点Q), y y y值变化缓慢。
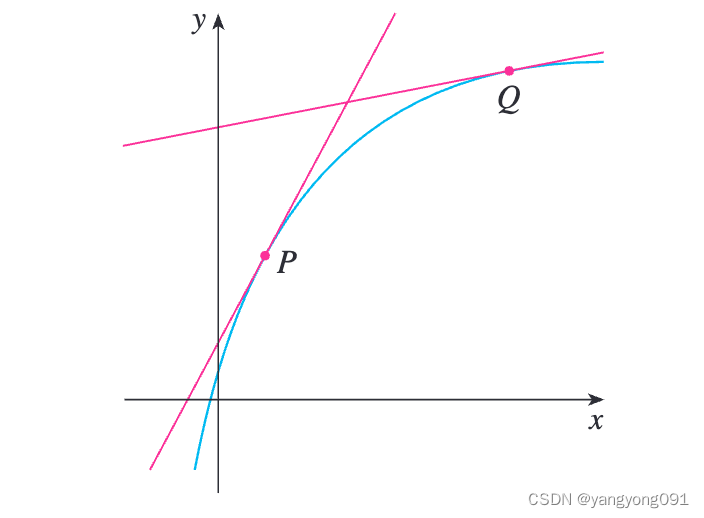
例六
制造商生产固定宽度的织物卷,生产 x x x 码织物的成本是 C ( x ) C(x) C(x) 美元。
(a) 导数 f ’ ( x ) f’(x) f’(x) 的含义是什么?它的单位是什么?
(b) 在实际中,说 f ’ ( 1000 ) = 9 f’(1000) = 9 f’(1000)=9 是什么意思?
(c) 你认为哪个大, f ’ ( 50 ) f’(50) f’(50) 还是 f ’ ( 500 ) f’(500) f’(500)或 f ’ ( 5000 ) f’(5000) f’(5000) 呢?
例七
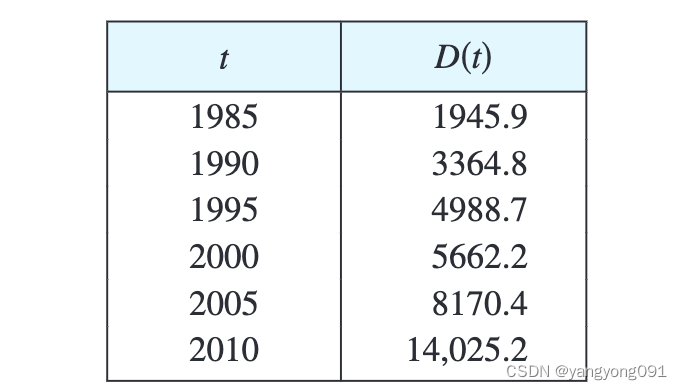
让 D ( t ) D(t) D(t)表示时间 t t t时的美国国债。表格提供了从1985年到2010年每年底的估算值,单位为十亿美元。解释并估算 D ′ ( 2000 ) D\prime(2000) D′(2000)的值。
解:
导数 D ’ ( 2000 ) D’(2000) D’(2000) 表示国债 D D D 相对于时间 t t t 在 t = 2000 t = 2000 t=2000 时的变化率,即2000年国债的增长率。根据变化率方程有
D ′ ( 2000 ) = lim t → 2000 D ( t ) − D ( 2000 ) t − 2000 D{\prime}(2000) = \lim_{t \to 2000} \frac{D(t) - D(2000)}{t - 2000} D′(2000)=t→2000limt−2000D(t)−D(2000)
因此,我们计算并列出差商(平均变化率)的数值如下。
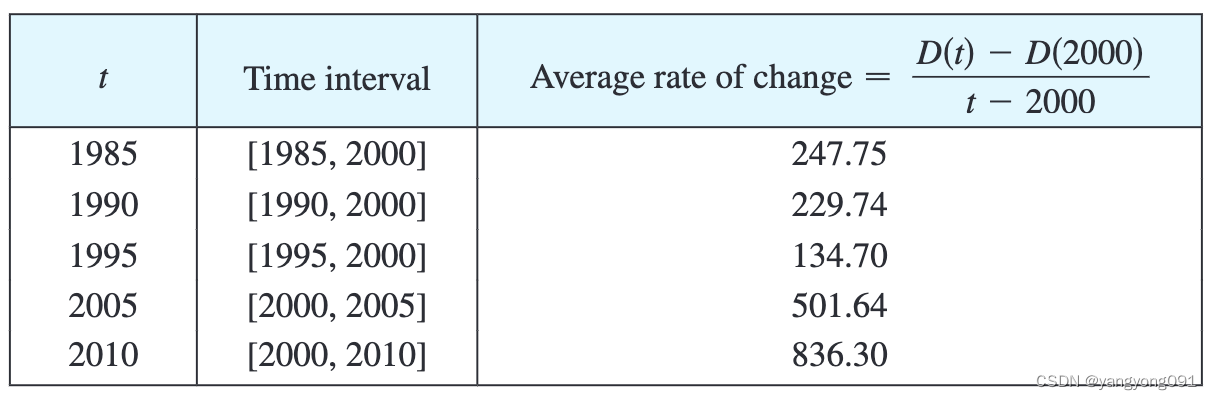
从这张表格中我们可以看出, D ′ ( 2000 ) D{\prime}(2000) D′(2000)大约在每年 134.7 134.7 134.7亿到 501.64 501.64 501.64亿美元之间。【在这里,我们做出一个合理的假设,即债务在1995年到2005年之间没有剧烈波动。】我们估计美国国债在2000年的增长率大约是这两个数字的平均值,即 D ′ ( 2000 ) ≈ 318 亿美元每年 D'(2000) \approx 318亿美元每年 D′(2000)≈318亿美元每年








![[吃瓜教程]概览西瓜书+南瓜书第3章线性回归](https://img-blog.csdnimg.cn/direct/a260a63b8b094733969cd8f353f394e3.png)





![[巨详细]使用HBuilder-X新建uniapp项目教程](https://img-blog.csdnimg.cn/direct/a661158f25d145909719097e881d1327.png)
