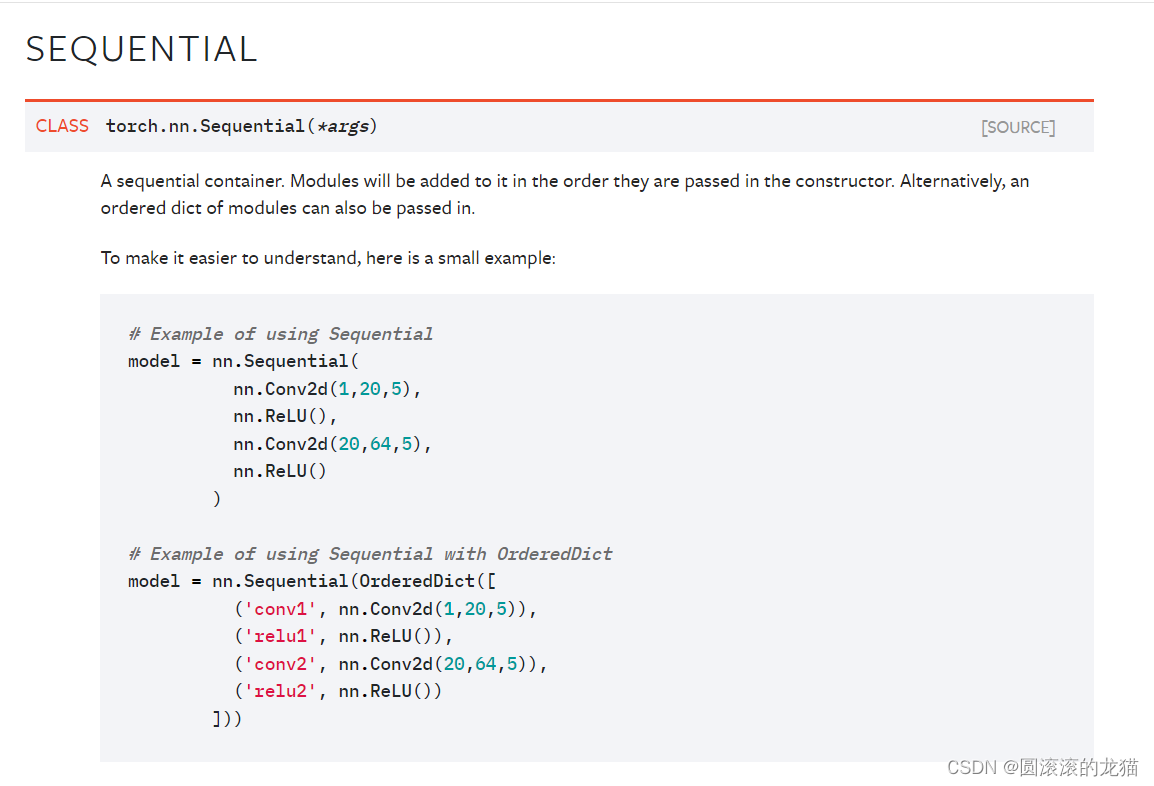
链接:https://pytorch.org/docs/1.8.1/generated/torch.nn.Sequential.html#torch.nn.Sequential
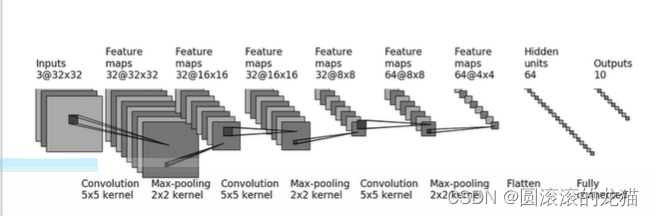
完成这样一个网络模型
第一步新建一个卷积层
self.conv1=Conv2d(3,32,5)#第一步将33232输出为32通道,卷积核5*5
注意一下:输出通道数等于卷积核个数,与输入通道数无关

注意shape式子中的dilation,代表内核元素之间的间距。默认值:1,dilation参数用于指定卷积核内部元素之间的间距。当dilation参数为0时,表示普通的卷积操作,即卷积核内部的元素是相邻的,没有间隔。区别主要体现在dilation参数大于1时,即空洞卷积(dilated convolution)的情况下,此时卷积核内的元素之间会有间隔,从而扩大了卷积核的感受野。。
当dilation参数为1时,也表示普通的卷积操作,即卷积核内部的元素是相邻的,没有间隔。
空洞卷积(dilated convolution)是一种卷积操作,通过在卷积核中插入间隔(洞)来增加感受野(receptive field),而不增加参数数量。相比于普通卷积,空洞卷积在保持参数量相对较小的情况下可以有效地扩大网络感受野。这种操作在处理具有大尺寸输入和大跨度特征的情况下特别有用。
奇数卷积核 直接用kernel_size // 2计算
在卷积神经网络中,卷积核的大小通常是一个正整数,例如3x3、5x5等。当卷积核的大小是奇数时,意味着卷积核的中心位置是准确地位于核的中心的一个单元的位置上。
使用奇数大小的卷积核有一些优点,其中之一是因为有一个确切的中心位置,可以更容易地确定卷积核是如何应用于输入图像的。此外,奇数大小的卷积核也有助于确保输出的特征图中的像素位置是对称分布的。
在一些情况下,为了方便地计算卷积核的填充(padding),可以利用奇数卷积核的特点直接使用 kernel_size // 2 这样的计算来确定卷积核中心相对于卷积核边缘的偏移量。这种方式常用于对称地填充卷积操作,以保持输入和输出的大小一致。
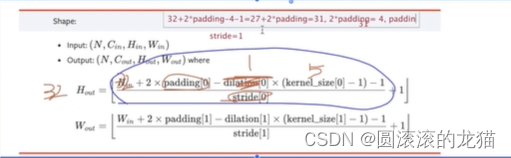
可以这样估算
也可以
奇数卷积核把中心格子对准图片第一个格子,卷积核在格子外有两层就padding=2,设置padding是为了提高边缘利用率
然后依次按图进行构造
构建一个网络
import torch
from torch import nn
from torch.nn import Conv2d, MaxPool2d, Flatten, Linearclass Tudui(nn.Module):def __init__(self) -> None:super().__init__()self.conv1=Conv2d(3,32,5,padding=2)#第一步将3*32*32输出为32通道,卷积核5*5self.maxpool1=MaxPool2d(2)#池化核2x2self.conv2=Conv2d(32,32,5,padding=2)self.maxpool2=MaxPool2d(2)self.conv3=Conv2d(32,64,5,padding=2)self.maxpool3=MaxPool2d(2)self.flatten=Flatten()self.linear=Linear(1024,64)self.linear2=Linear(64,10)def forward(self, x):x = self.conv1(x)x = self.maxpool1(x)x = self.conv2(x)x = self.maxpool2(x)x = self.conv3(x)x = self.maxpool3(x)x = self.flatten(x)x = self.linear(x)x = self.linear2(x)return xtudui=Tudui()
print(tudui)#检验网络是否搭建成功了
input=torch.ones((64,3,32,32))
output=tudui(input)
print(output.shape)Linear时自己算出来的,算不出的话
import torch
from torch import nn
from torch.nn import Conv2d, MaxPool2d, Flatten, Linearclass Tudui(nn.Module):def __init__(self) -> None:super().__init__()self.conv1=Conv2d(3,32,5,padding=2)#第一步将3*32*32输出为32通道,卷积核5*5self.maxpool1=MaxPool2d(2)#池化核2x2self.conv2=Conv2d(32,32,5,padding=2)self.maxpool2=MaxPool2d(2)self.conv3=Conv2d(32,64,5,padding=2)self.maxpool3=MaxPool2d(2)self.flatten=Flatten()def forward(self, x):x = self.conv1(x)x = self.maxpool1(x)x = self.conv2(x)x = self.maxpool2(x)x = self.conv3(x)x = self.maxpool3(x)x = self.flatten(x)# x = self.linear(x)# x = self.linear2(x)return xtudui=Tudui()
print(tudui)#检验网络是否搭建成功了
input=torch.ones((64,3,32,32))
output=tudui(input)
print(output.shape)看一下output,在flatten后的输出是1024个
import torch
from torch import nn
from torch.nn import Conv2d, MaxPool2d, Flatten, Linear, Sequentialclass Tudui(nn.Module):def __init__(self) -> None:super().__init__()self.sequential=Sequential(Conv2d(3,32,5,padding=2),MaxPool2d(2),Conv2d(32,32,5,padding=2),MaxPool2d(2),Conv2d(32, 64, 5, padding=2),MaxPool2d(2),Flatten(),Linear(1024,64),Linear(64,10))def forward(self, x):x = self.sequential(x)return xtudui=Tudui()
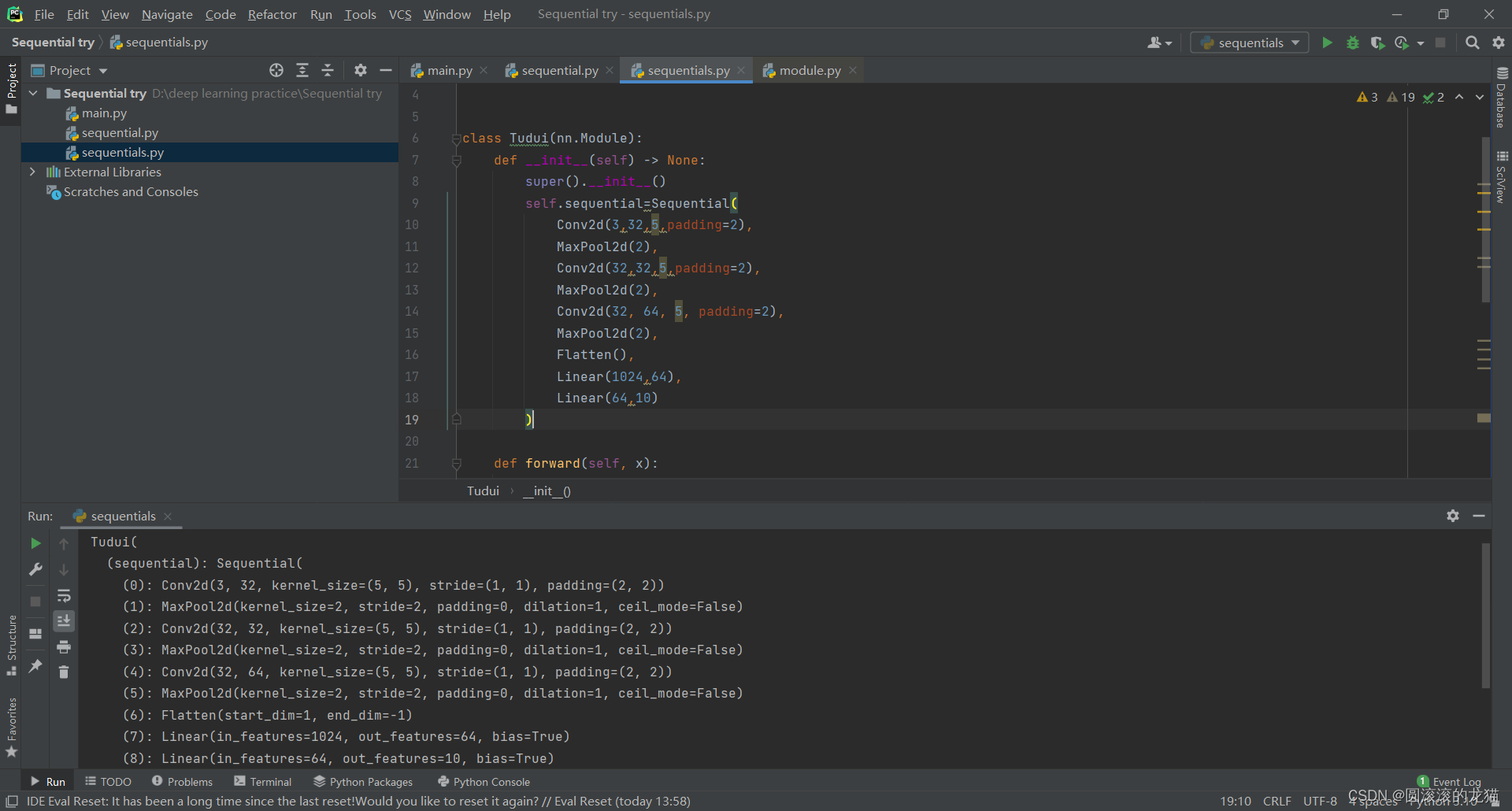
print(tudui)#检验网络是否搭建成功了
input=torch.ones((64,3,32,32))
output=tudui(input)
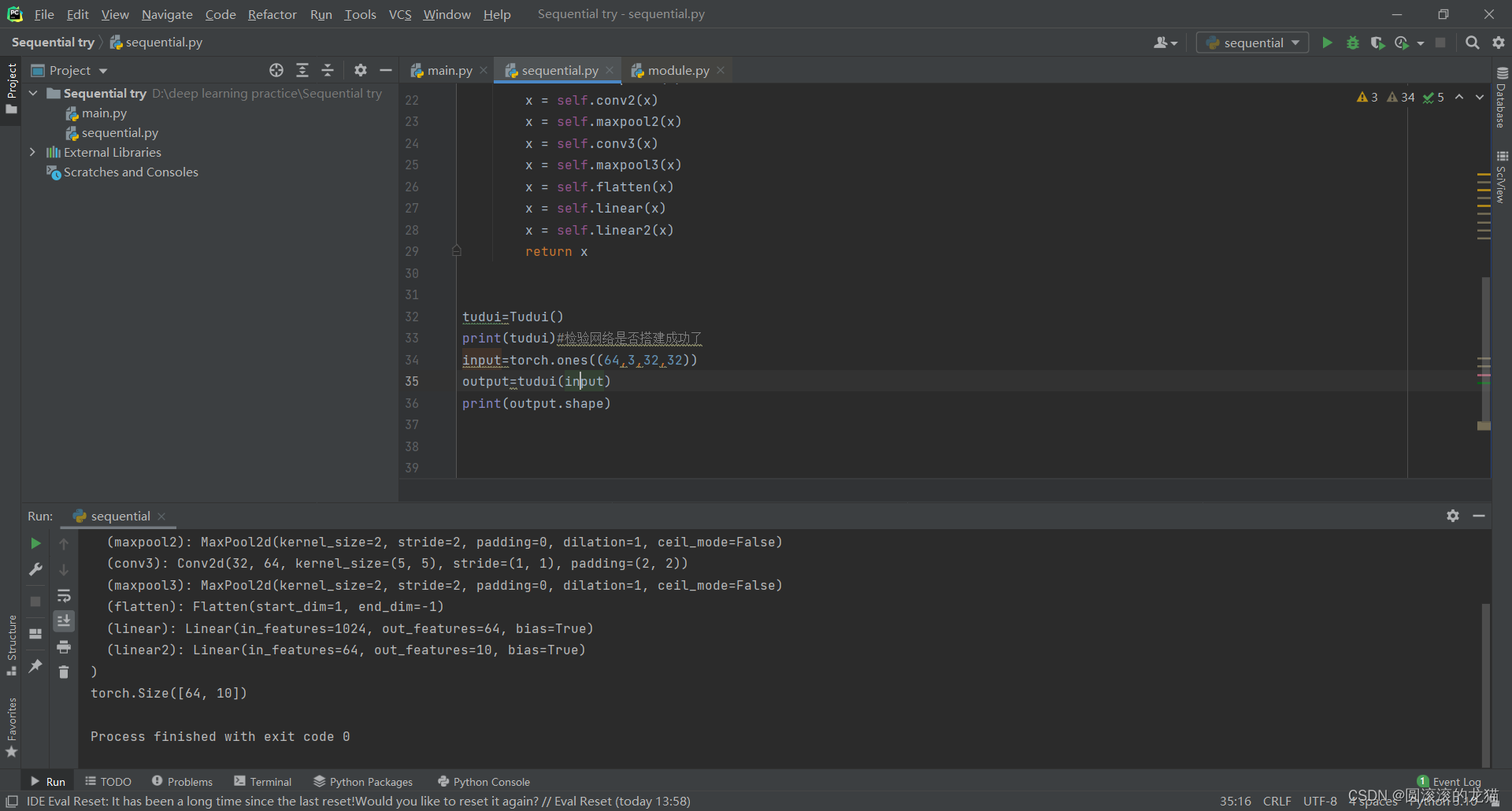
print(output.shape)这是另一个写法可以看到这个 写法比上面优雅的多,输出也会更整齐
添加入tensorboard
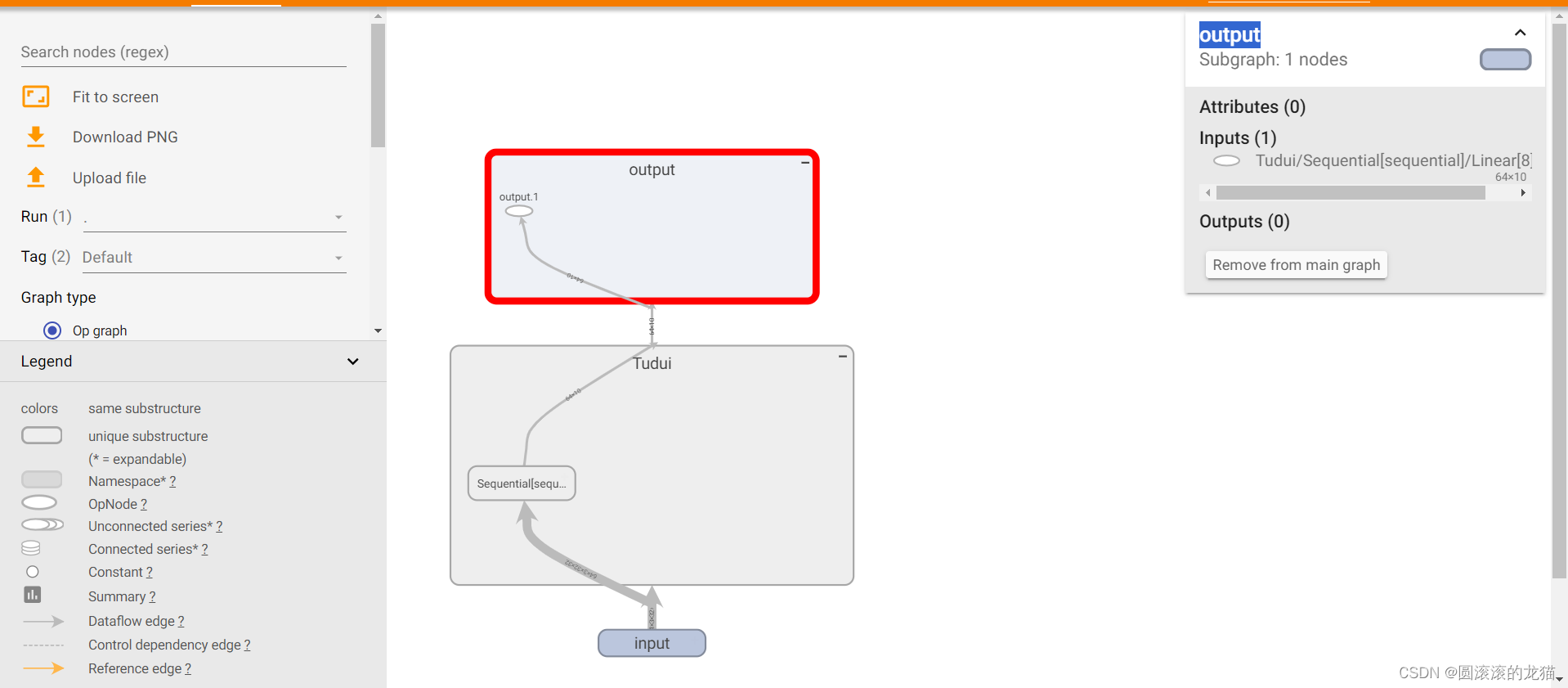
可以看到网络结构
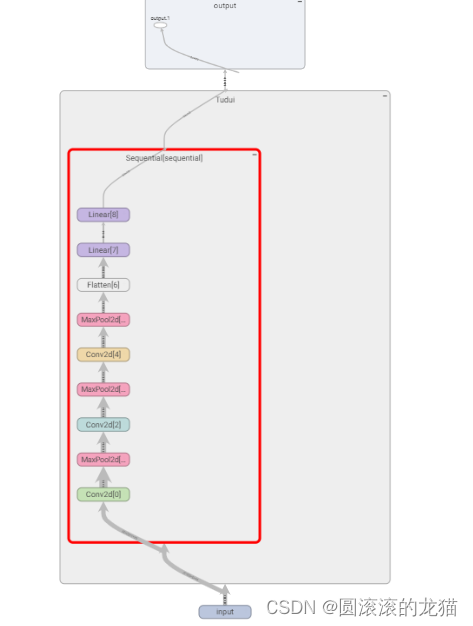
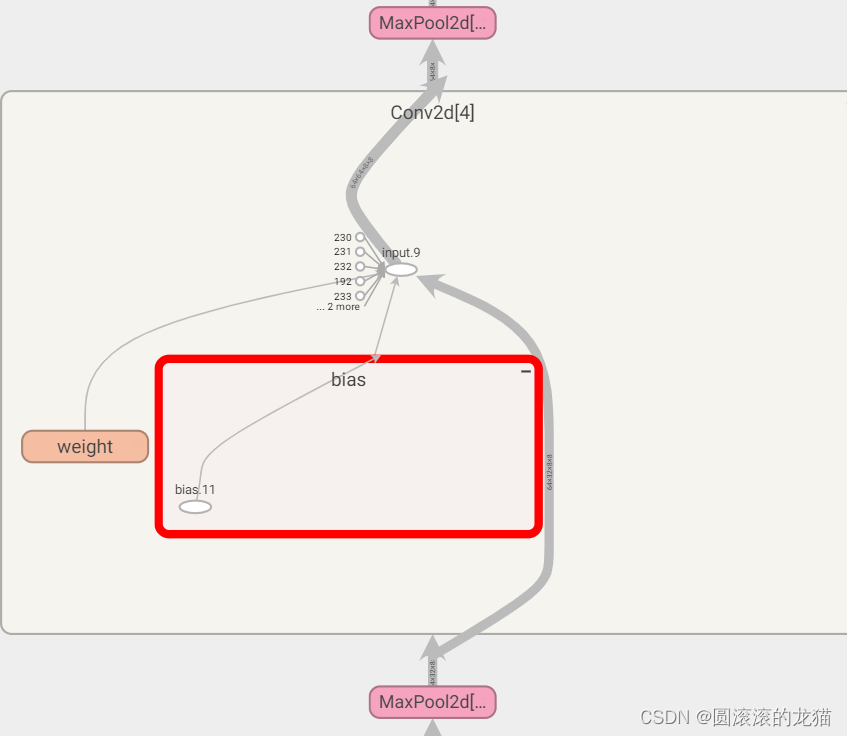
如此可以看到一些需要的参数