算法基础精选题单动态规划（dp）（递推+线性dp）（个人题解）

前言：

一些简单的dp问题。

正文：

题单：237题】算法基础精选题单_ACM竞赛_ACM/CSP/ICPC/CCPC/比赛经验/题解/资讯_牛客竞赛OJ_牛客网 (nowcoder.com)

递推：

NC235911 走楼梯：

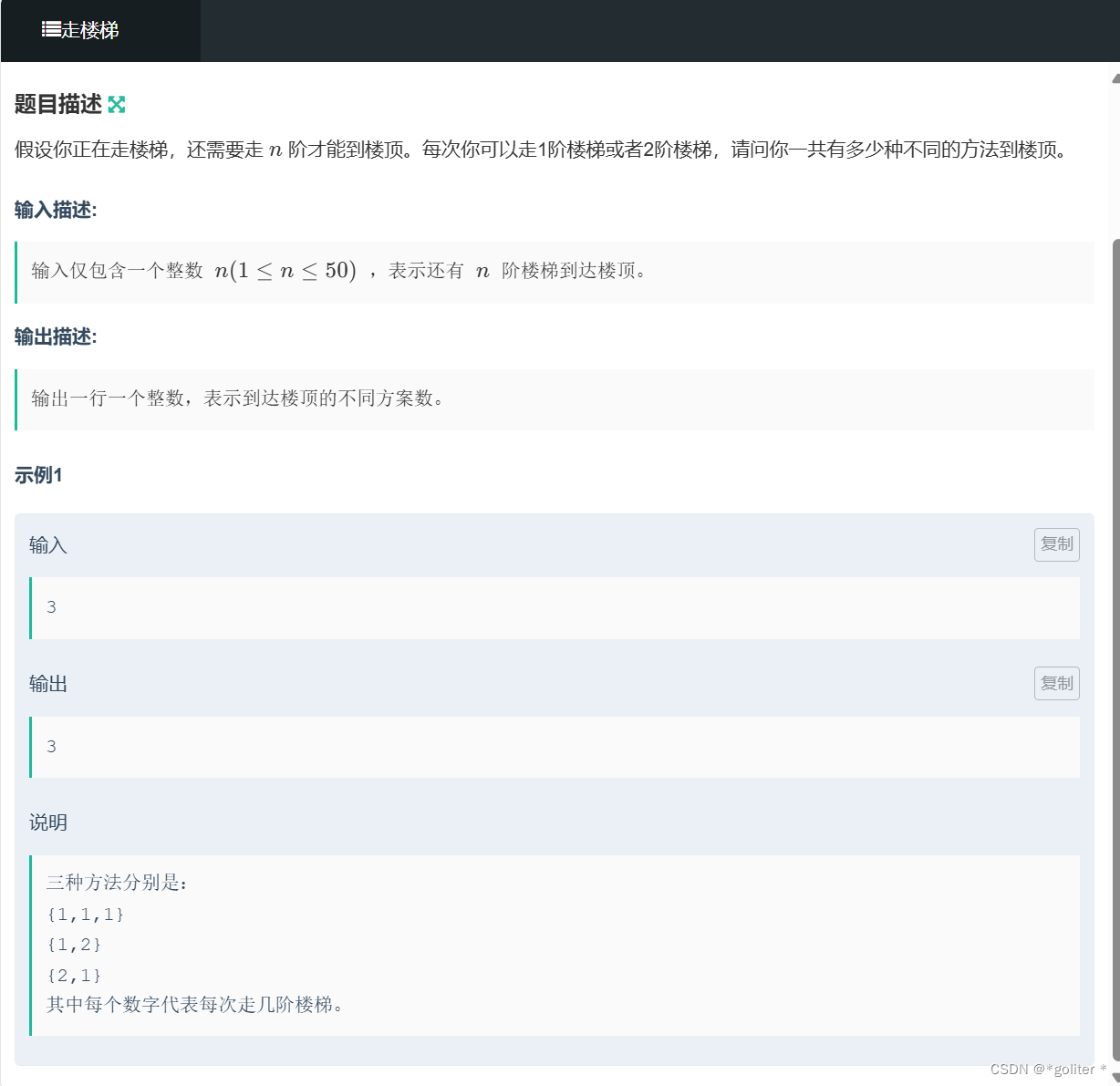
#include<bits/stdc++.h>
using namespace std;
long long dp[150];
int main(){int n;cin>>n;dp[1]=1;dp[0]=1;for(int i=2;i<=n;i++){dp[i]=dp[i-1]+dp[i-2];}cout<<dp[n];return 0;
}

dp中最经典的问题，就不展开说了。

线性dp：

NC22096 数字三角形：

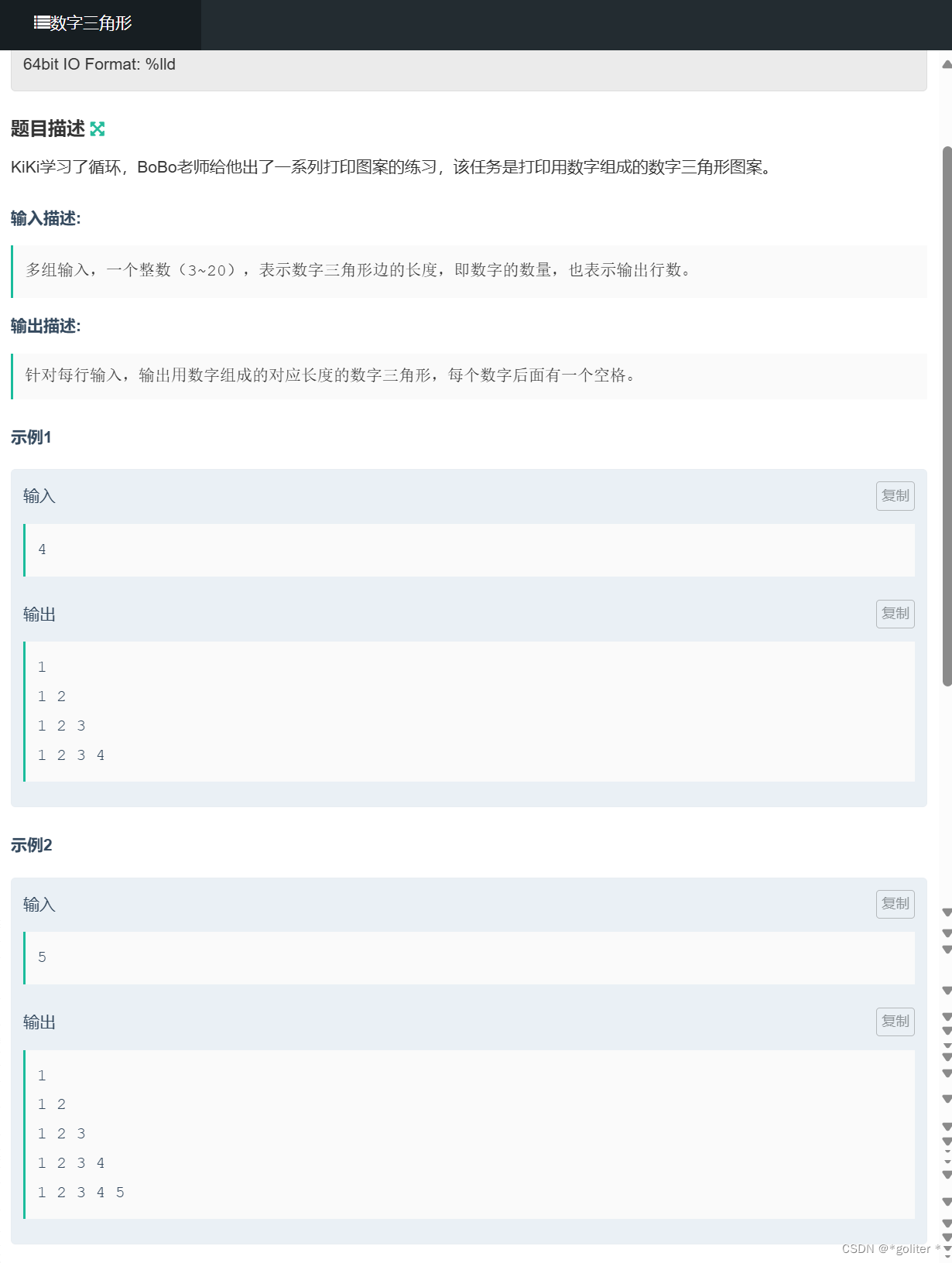
#include<bits/stdc++.h>
using namespace std;
int main(){int n;while(cin>>n){for(int i=1;i<=n;i++){for(int j=1;j<=i;j++){cout<<j<<" ";}cout<<endl;}}return 0;
}

这题不知道和dp有什么关系，直接两层循环输出就行了。

NC16708 过河卒：

#include<bits/stdc++.h>
using namespace std;
long long dp[55][55];
void con(int x,int y){dp[x][y]=-1;if(x+1>=0&&y+2>=0)dp[x+2][y+1]=-1;if(x+2>=0&&y+1>=0)dp[x+1][y+2]=-1;if(x+2>=0&&y+1>=0)dp[x-1][y+2]=-1;if(x-2>=0&&y+1>=0)dp[x-2][y+1]=-1;if(x-2>=0&&y-1>=0)dp[x-2][y-1]=-1;if(x-1>=0&&y-2>=0)dp[x-1][y-2]=-1;if(x+1>=0&&y-2>=0)dp[x+1][y-2]=-1;if(x+2>=0&&y-1>=0)dp[x+2][y-1]=-1;
}
int main(){int n,m,x,y;cin>>n>>m>>x>>y;con(x+1,y+1);dp[1][1]=1;for(int i=1;i<=21;i++){for(int j=1;j<=21;j++){if(dp[i][j]!=-1){if(dp[i-1][j]!=-1)dp[i][j]+=dp[i-1][j];if(dp[i][j-1]!=-1)dp[i][j]+=dp[i][j-1];}}}cout<<dp[n+1][m+1];return 0;
}

在地图上标记好马的位置与马能走到的另外八个位置，在状态转移的时候记得注意该点状态永远为0。最后输出终点的状态。

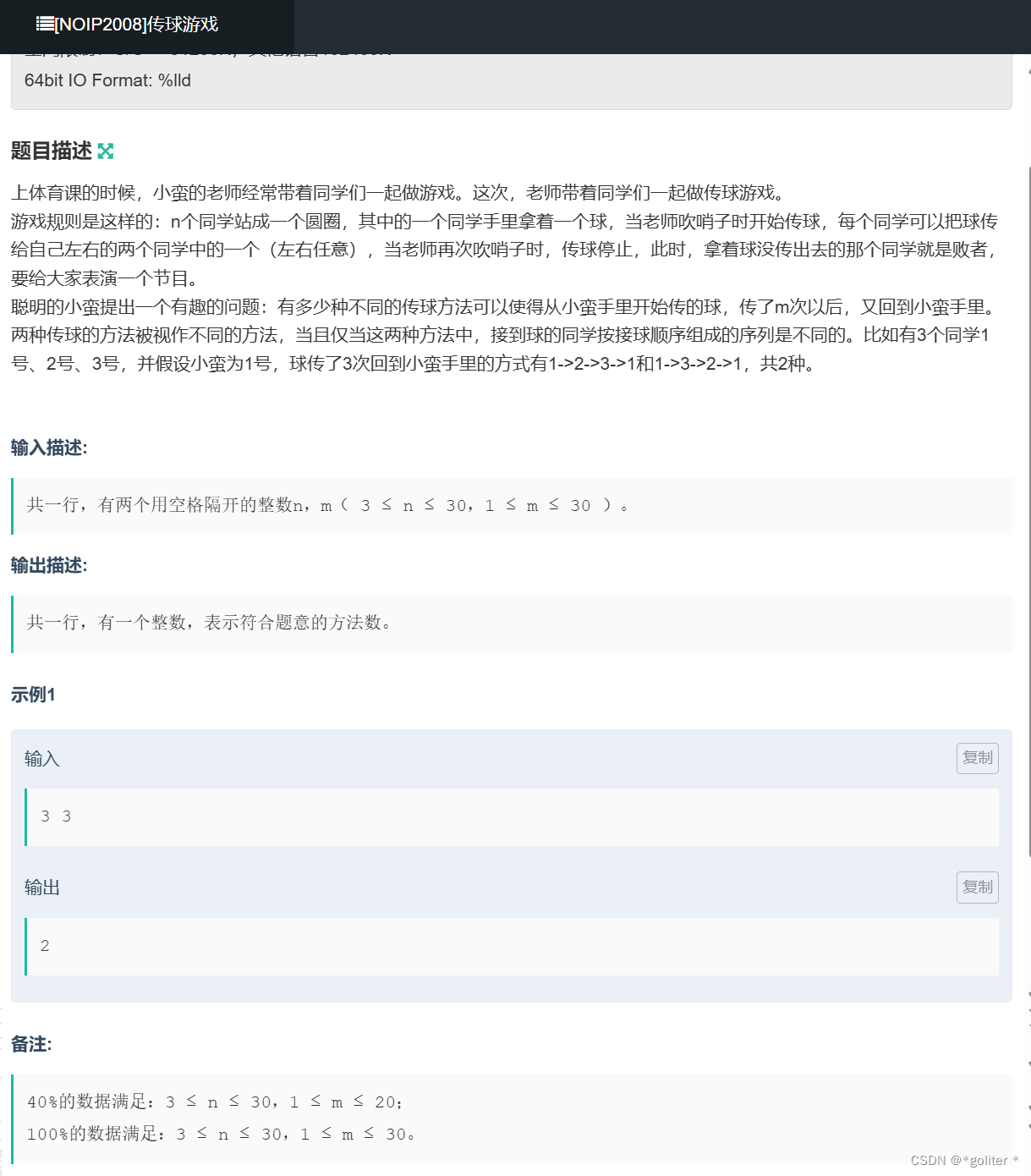
NC16619 传球游戏：

#include<bits/stdc++.h>
using namespace std;
int n,m;
long long dp[105][105];
int main(){cin>>n>>m;dp[0][1]=1;for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){if(j==1){dp[i][j]=dp[i-1][n]+dp[i-1][j+1];}else if(j==n){dp[i][j]=dp[i-1][1]+dp[i-1][j-1];}else{dp[i][j]=dp[i-1][j-1]+dp[i-1][j+1];}}}cout<<dp[m][1];return 0;
}

dp[i][j]表示在传球次数达到i次时球到达j手上的方法数，状态转移方程我们可以由球只能从左右两侧传来，所以知方程dp[i][j]=dp[i-1][j-1]+dp[i-1][j+1]，注意特判j=1和n的情况。

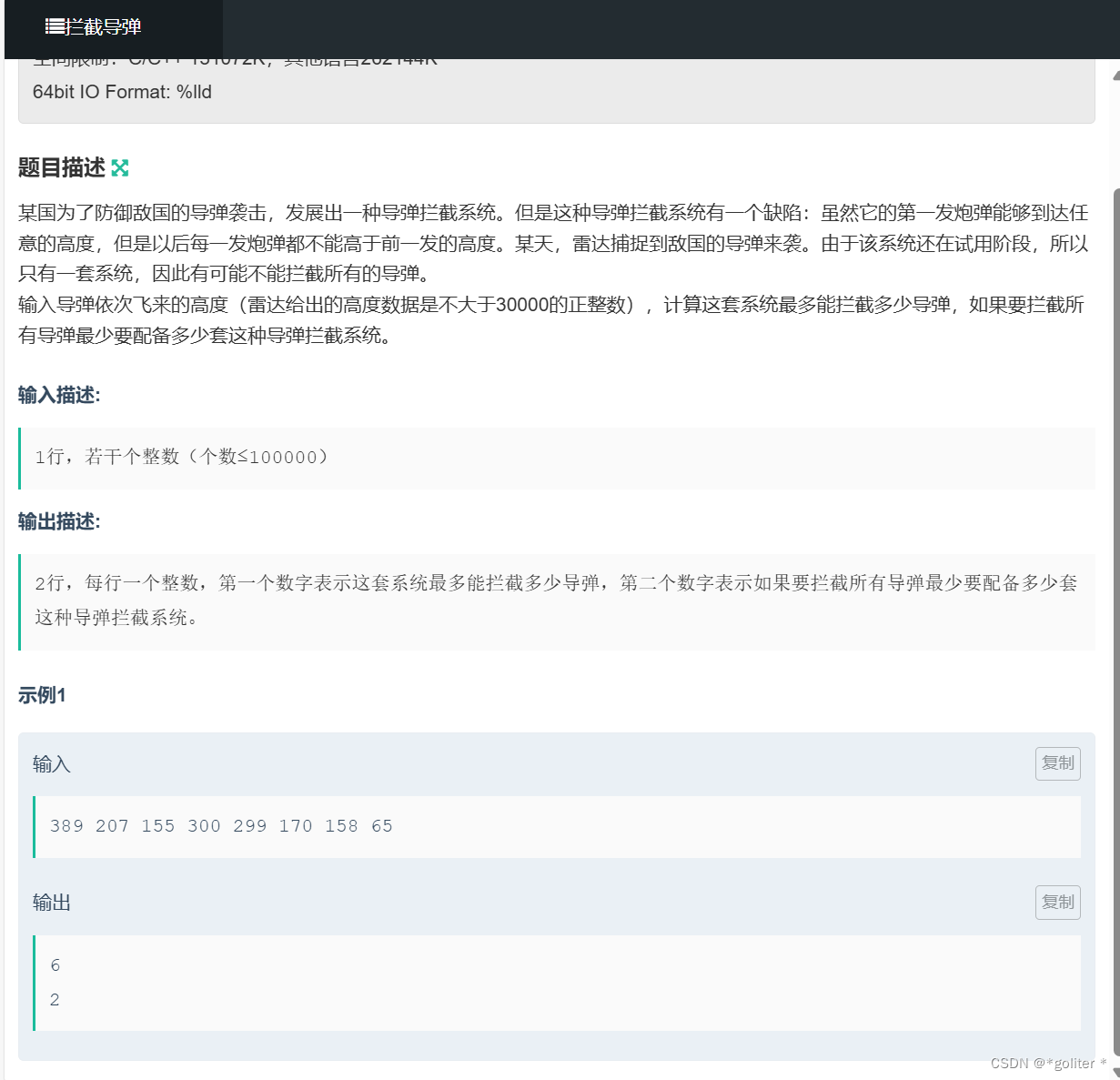
NC16810 [NOIP1999]拦截导弹：

#include <bits/stdc++.h>
using namespace std;
int a[1001],dp[1001];
int main()
{int p=0,flag=0;while(cin>>a[++p]){}p--;int ans=0;for(int i=1;i<=p;i++){ flag=0;for(int j=i-1;j>=1;j--)if (a[i]<=a[j]) flag=max(flag,dp[j]);if (flag==0) dp[i]=1;else dp[i]=flag+1;ans=max(ans,dp[i]);//cout<<dp[i]<<endl;}cout<<ans<<endl;memset(dp,0,sizeof(dp));ans=0;for(int i=1;i<=p;i++){ flag=0;for(int j=i-1;j>=1;j--)if (a[i]>a[j]) flag=max(flag,dp[j]);if (flag==0) dp[i]=1;else dp[i]=flag+1;ans=max(ans,dp[i]);//cout<<dp[i]<<endl;}cout<<ans<<endl;return 0;
}

Dilworth定理：最小链覆盖=最长反链长度，所以需要的系统就为这个序列的最长上升列长度，而一个系统最多能拦截的值就为反转的数列的最长上升子序列长度。求两个最长上升子序列即可。

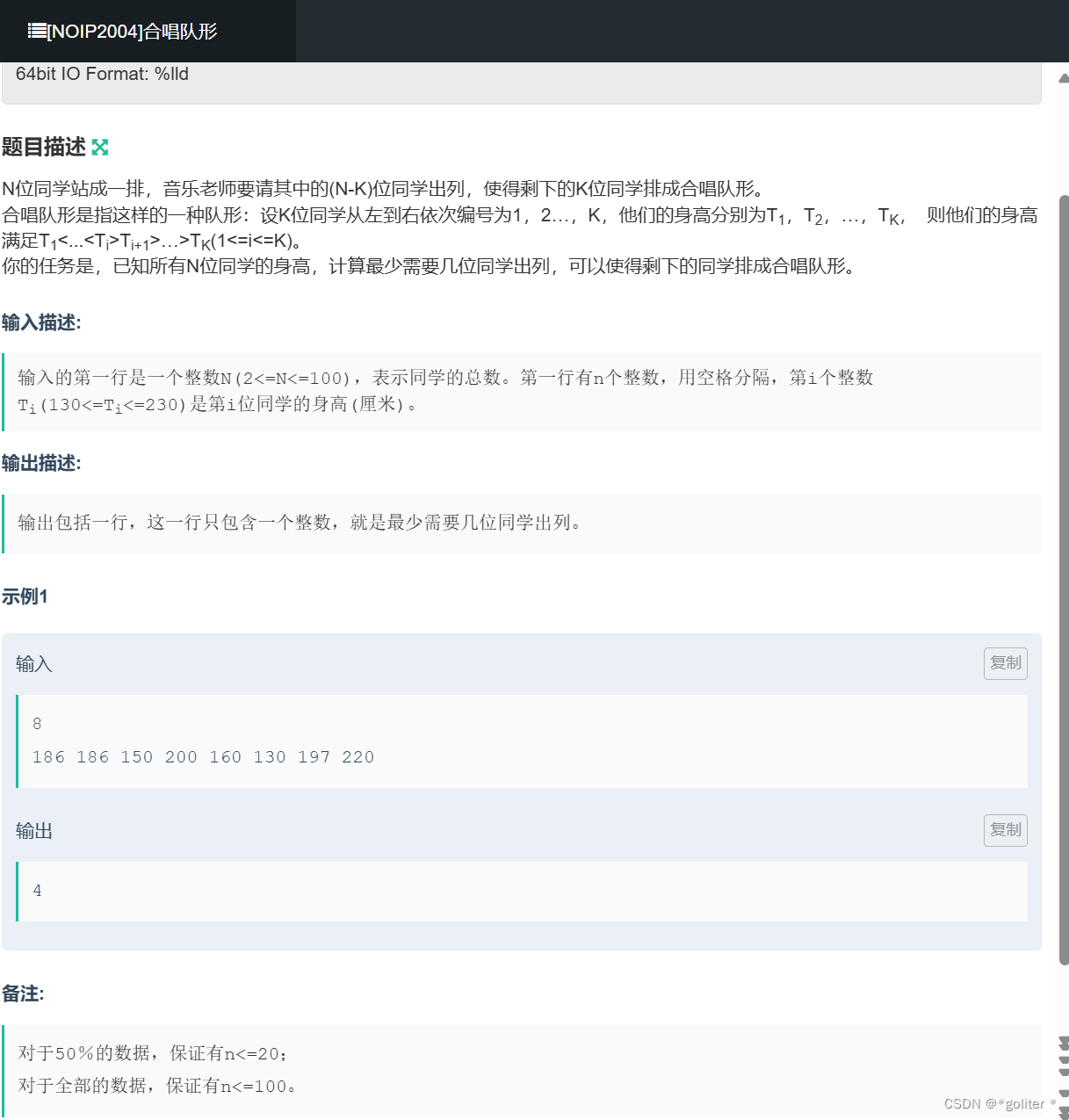
NC16664 [NOIP2004]合唱队形：

#include<bits/stdc++.h>
using namespace std;
int a[1005];int dp1[1005],dp2[1005];
int main(){int n,ans=0;cin>>n;for(int i=1;i<=n;i++){cin>>a[i];}dp1[1]=1;for(int i=1;i<=n;i++){int m=0;for(int j=1;j<i;j++){if(a[i]>a[j]&&dp1[j]>m)m=dp1[j];//cout<<dp1[i]<<endl;}dp1[i]=m+1;}dp2[n]=1;for(int i=n;i;i--){int m=0;for(int j=n;j>i;j--){if(a[i]>a[j]&&dp2[j]>m)m=dp2[j];}dp2[i]=m+1;}for(int i=1;i<=n;i++){ans=max(ans,dp1[i]+dp2[i]-1);}//cout<<n<<" "<<ans<<endl;cout<<n-ans<<endl;return 0;
}

最长上升子序列的变式。先从左往右求一遍最长上升子序列(dp1)，再从右往左求一遍(dp2)。
结果遍历一遍从左和从右的dp值和(dp1[i]+dp2[i])，找出和为最大的即为最大正常先递增再递减的子序列长度。

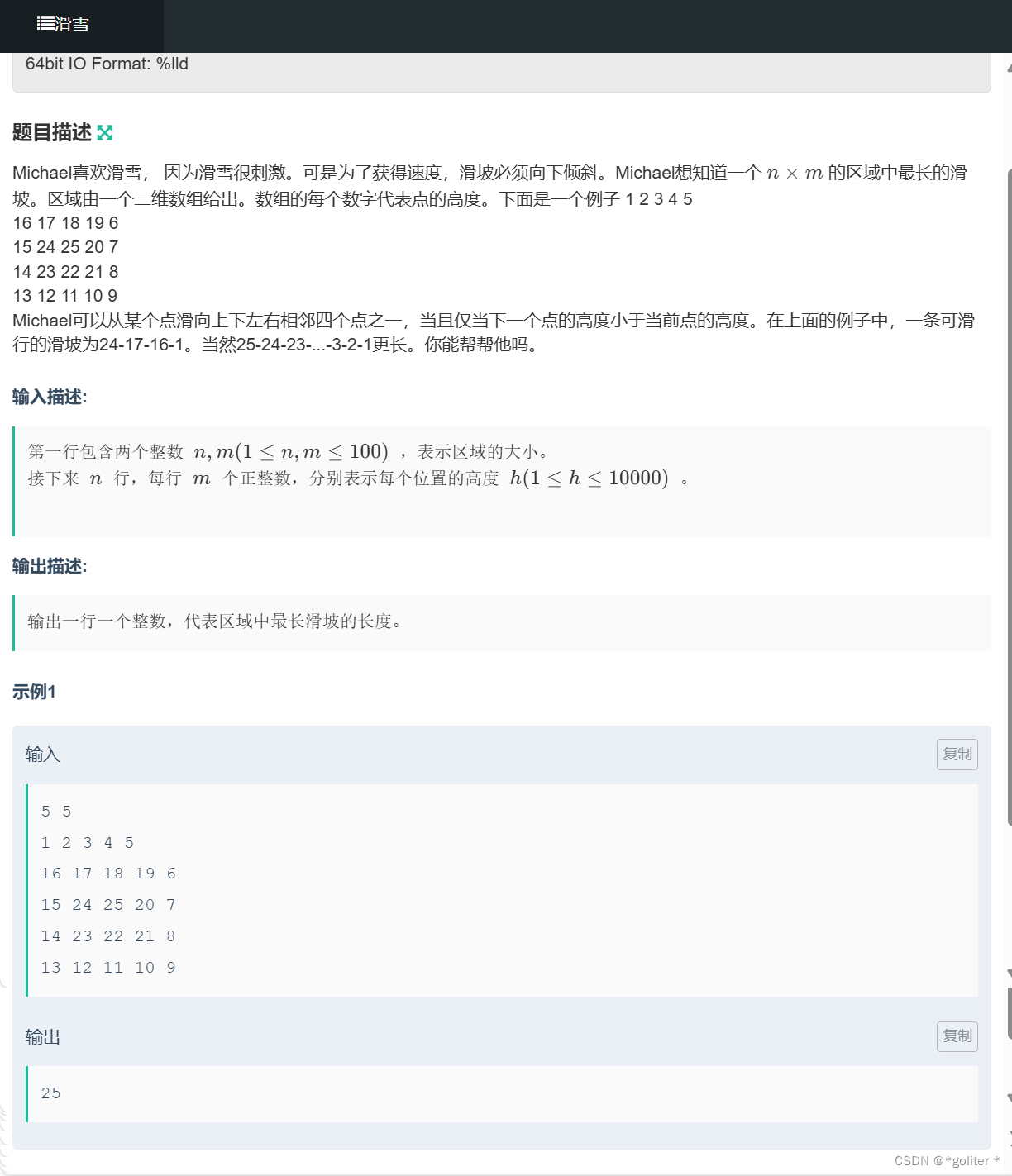
NC235954 滑雪：

#include<bits/stdc++.h>
using namespace std;
const int N = 310;
int n, m;
int g[N][N];
int f[N][N];
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
int dp(int x, int y){int &v = f[x][y];if (v != -1) return v;v = 1;for (int i = 0; i < 4; i ++ ){int a = x + dx[i], b = y + dy[i];if (a >= 1 && a <= n && b >= 1 && b <= m && g[x][y] > g[a][b])v = max(v, dp(a, b) + 1);}return v;
}int main(){cin>>n>>m;for (int i = 1; i <= n; i ++ )for (int j = 1; j <= m; j ++ )scanf("%d", &g[i][j]);memset(f, -1, sizeof f);int res = 0;for (int i = 1; i <= n; i ++ )for (int j = 1; j <= m; j ++ )res = max(res, dp(i, j));printf("%d\n", res);return 0;
}

经典的记忆化搜索的题，我觉得比起dp更像搜索。从最高点开始向四周搜索，结束时一定是最长的路径在dp中，因为搜索结束了就表示最长的那条线已经走完了。

NC235948 最大子串和：

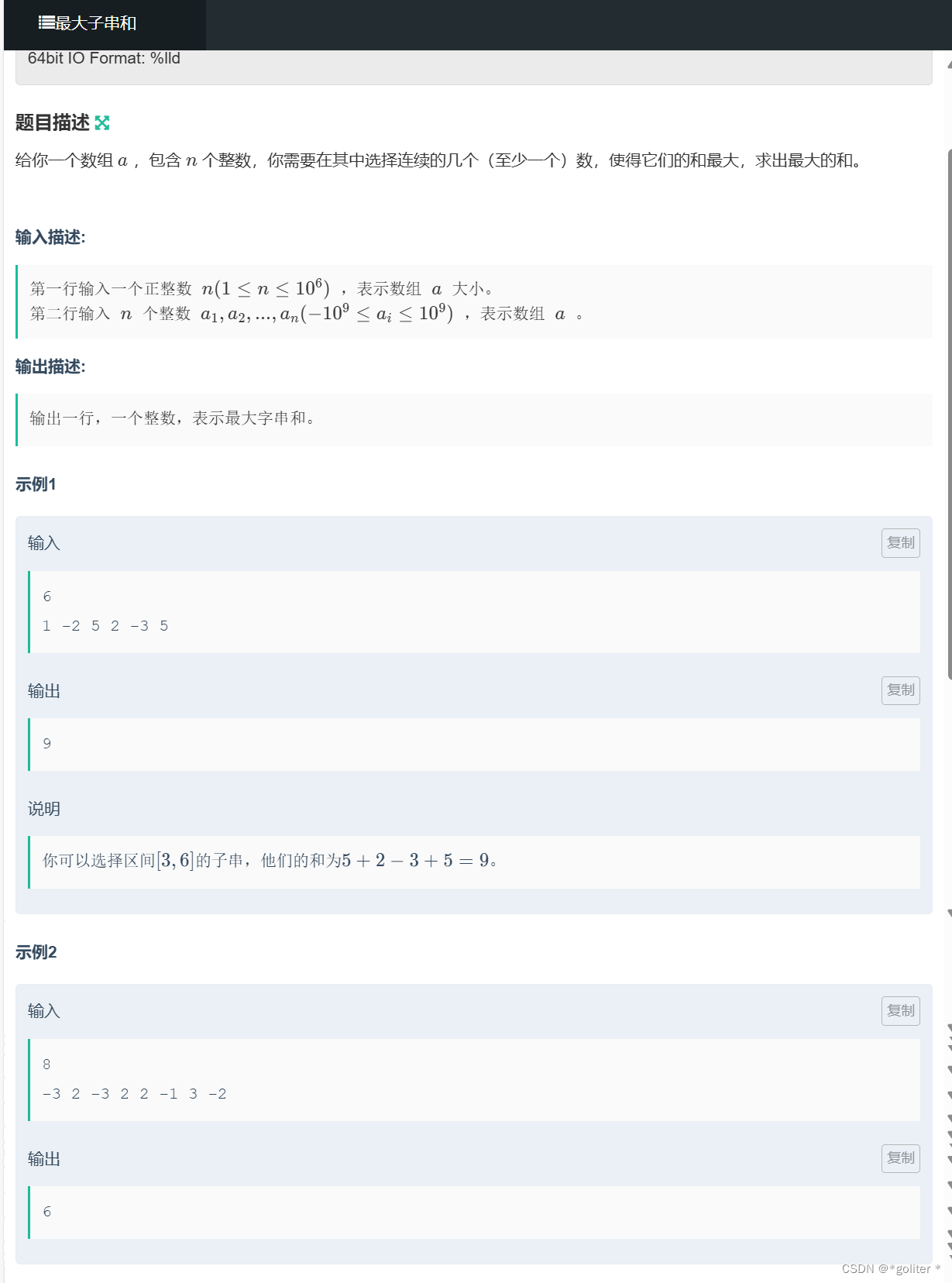
#include<bits/stdc++.h>
using namespace std;
long long a[1000005],dp[1000005];
int main(){long long n,ans=0;cin>>n;for(int i=1;i<=n;i++){cin>>a[i];dp[i]=max(dp[i-1]+a[i],dp[i]);ans=max(ans,dp[i]);}cout<<ans;return 0;
}

从某一个数字来看，它的最大连续子串和是前面一个数字的最大连续子串和加上它本身，和他本身取较大的那一个。当位于第一个的时候自然就是他自身所以可以实现一个动态规划。故递推式：dp[i] = max(dp[i-1]+dp[i], dp[i])。

NC235624 牛可乐和最长公共子序列：

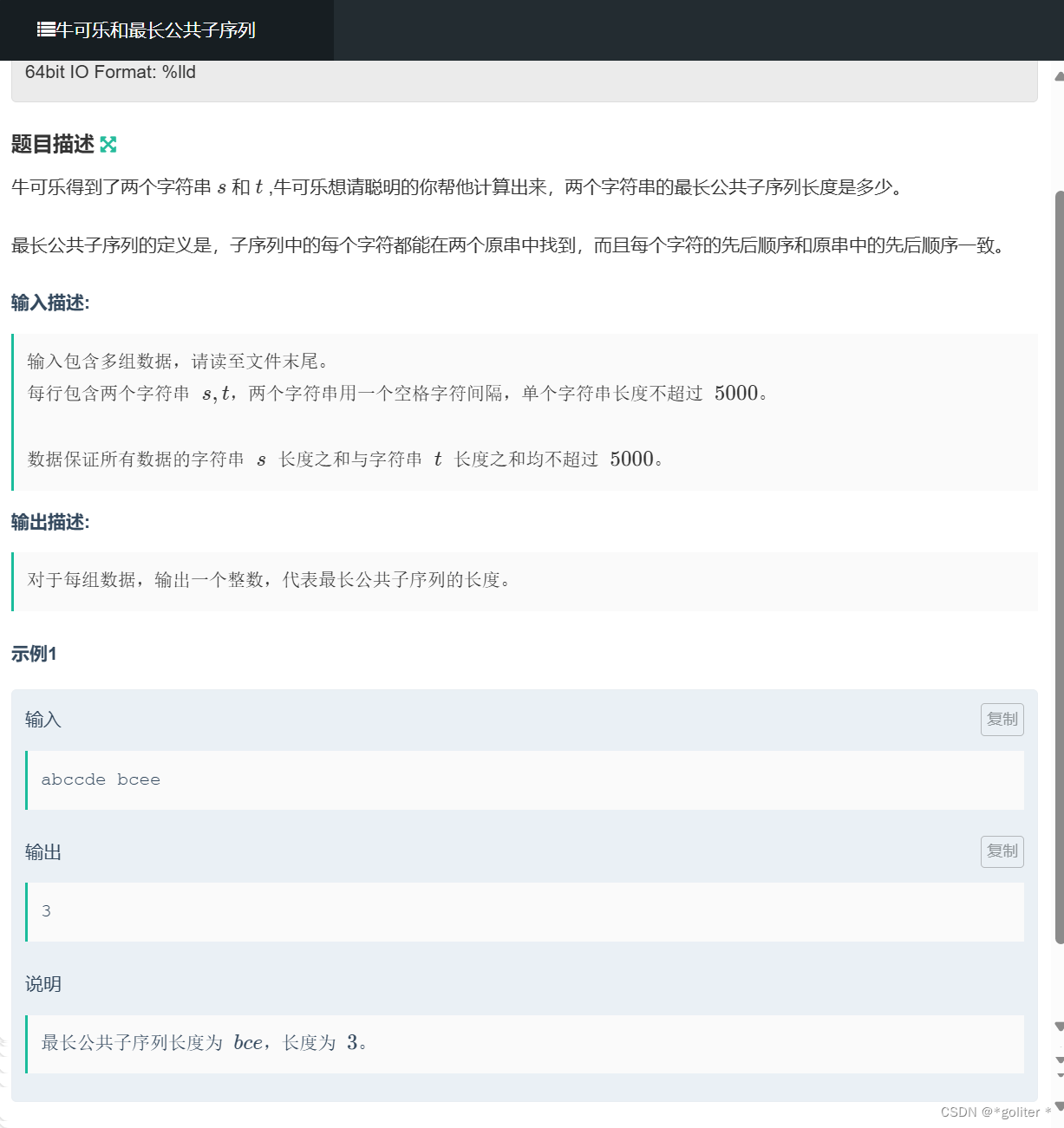
#include<bits/stdc++.h>
using namespace std;
int dp[5005][5005];
int main(){string s,t;while(cin>>s>>t){if(s[0]==t[0])dp[1][1]=1;int ans=0;//memset(dp,0,sizeof(dp));int n=s.size(),m=t.size();for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(s[i-1]==t[j-1])dp[i][j]=dp[i-1][j-1]+1;else dp[i][j]=max(dp[i][j-1],dp[i-1][j]);ans=max(dp[i][j],ans);}}cout<<ans<<endl;}return 0;
}

最长上升子序列的模板题。