【Leetcode每日一题】 01背包 - DP41 【模板】01背包（难度⭐⭐）（80）

1. 题目解析

题目链接：DP41 【模板】01背包

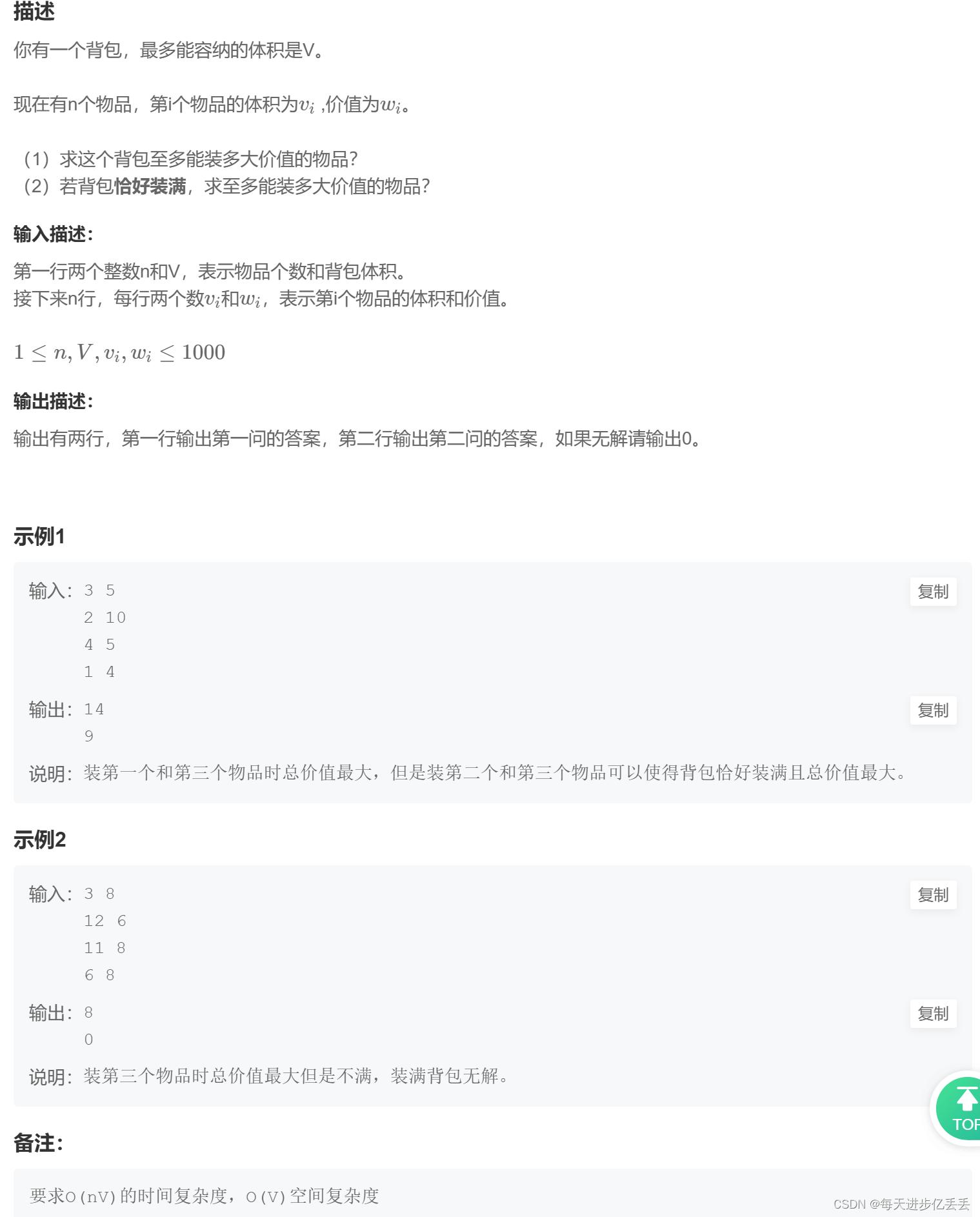
这个问题的理解其实相当简单，只需看一下示例，基本就能明白其含义了。

2.算法原理

第一问：不超过总体积的背包问题

1. 状态表示

dp[i][j] 表示：从前 i 个物品中挑选，总体积不超过 j 的所有选法中，能挑选出来的最大价值。

2. 状态转移方程

不选第 i 个物品：此时 dp[i][j] 等于从前 i-1 个物品中挑选，并且总体积不超过 j 的最大价值，即 dp[i][j] = dp[i - 1][j]。
选择第 i 个物品：需要确保选择该物品后总体积不超过 j，即 j >= v[i]。此时 dp[i][j] 等于从前 i-1 个物品中挑选，总体积不超过 j - v[i] 的最大价值加上第 i 个物品的价值，即 dp[i][j] = dp[i - 1][j - v[i]] + w[i]。

综合两种情况，状态转移方程为：

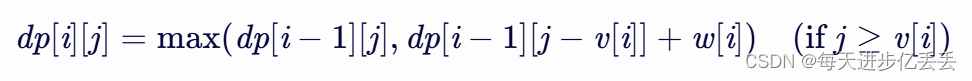
3. 初始化

为了简化边界条件，我们在数组顶部额外增加一行，并将这一行初始化为 0。因为不选择任何物品时，无论背包体积如何，价值都是 0。

4. 填表顺序

根据状态转移方程，我们从上到下、从左到右填表即可。

5. 返回值

最终返回 dp[n][V]，即从 n 个物品中选择，总体积不超过 V 的最大价值。

第二问：正好总体积的背包问题

1. 状态表示

dp[i][j] 表示：从前 i 个物品中挑选，总体积正好等于 j 的所有选法中，能挑选出来的最大价值。

2. 状态转移方程

类似地，我们有不选和选第 i 个物品两种情况。但这里需要注意的是，当选择第 i 个物品时，除了需要判断 j >= v[i]，还需要确保 dp[i - 1][j - v[i]] 是有效的（即不是初始化的无效值）。

状态转移方程为：

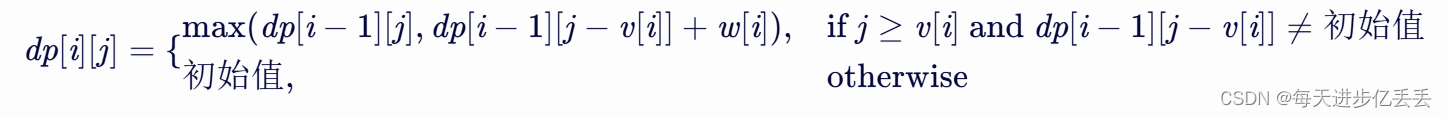
3. 初始化

同样，我们在数组顶部增加一行。第一行除了第一个元素（对应体积为 0 的情况）为 0 外，其余元素都设置为一个表示无效的初始值（如 -1）。

4. 填表顺序

依然是从上到下、从左到右填表。

5. 返回值

在返回最终答案前，需要判断 dp[n][V] 是否为初始值。如果是，则表示无法凑齐体积为 V 的背包；否则，返回 dp[n][V]。

3.代码编写

#include <iostream>
#include <cstring>
using namespace std;const int N = 1010;
int n, V, v[N], w[N];
int dp[N][N];int main() {cin >> n >> V;for (int i = 1; i <= n; i++)cin >> v[i] >> w[i];//第一问for (int i = 1; i <= n; i++) {for (int j = 0; j <= V; j++) {//以i结尾不选idp[i][j] = dp[i - 1][j];if (j >= v[i]) { //剩余空间足够//在前i-1个取出背包剩余j-v[i]最大值，dp[i][j]就代表前i个剩余J时的最大值dp[i][j] = max(dp[i][j], dp[i - 1][j - v[i]] + w[i]);}}}cout << dp[n][V] << endl;//第二问memset(dp, 0, sizeof dp);for (int j = 1; j <= V;j++) dp[0][j] = -1;//我们约定当前面凑不出刚好为j容量的物品是价值为-1，这里初始化表示取前0个物品，使得容量恰好为j，当j>0这不可能，所以初始化为-1for (int i = 1; i <= n; i++) {for (int j = 0; j <= V; j++) {//以i结尾不选idp[i][j] = dp[i - 1][j];if (j >= v[i] && dp[i - 1][j - v[i]] != -1) { //剩余空间足够//在前i-1个取出背包剩余j-v[i]最大值，dp[i][j]就代表前i个剩余J时的最大值dp[i][j] = max(dp[i][j], dp[i - 1][j - v[i]] + w[i]);}}}cout << (dp[n][V] == -1 ? 0 : dp[n][V]) << endl;return 0;
}