目录
最大坐标值
题目描述
输入描述
输出描述
示例1
输入
输出
说明
解析
答案
寻找最富裕的小家庭
题目描述
输入描述
输出描述
示例1
输入
输出
说明
解析
答案
两个字符串间的最短路径问题
题目描述
编辑
输入描述
输出描述
示例1
输入
输出
示例2
输入
输出
解析
答案
最大坐标值
考察参数校验,简单循环。
题目描述
小明在玩一个游戏,游戏规则如下:
在游戏开始前,小明站在坐标轴原点处(坐标值为0)。给定一组指令和一个幸运数,每个指令都是一个整数,小明按照指定的要求前进或者后退指定的步数。前进代表朝坐标轴的正方向走,后退代表朝坐标轴的负方向走。
幸运数为一个整数,如果某个指令正好和幸运数相等,则小明行进步数加1。
例如
幸运数为3,指令为[2,3,0,-5]
指令为2,表示前进2步;
指令为3,正好和幸运数相等,前进3+1=4步;
指令为0,表示原地不懂,既不前进,也不后退;
指令为-5,表示后退5步;
请你计算小明在整个游戏过程中,小明所处的最大坐标值。
输入描述
第一行输入一个数字,代表指定的总个数n(1<=n<=100)。
第二行输入一个数字,代表幸运数m(-100<=m<=100)。
第三行输入n个指定,每个指令值的取值范围为:-100<=指令值<=100.
输出描述
在整个游戏过程中,小明所处的最大坐标值。异常情况下输出:12345
示例1
输入
2
1
-5 1
输出
0
说明
总共 2 个指令,幸运数为 1 ,依照指令行进,依次如下:
游戏开始前,站在坐标轴原点,此时坐标值为 0 ;
指令为 −5 ,后退 5 步 ,此时坐标值为 −5 ;
指令为 1 ,正好等于幸运数,前进 1+1=2 步,此时坐标值为 −3;
整个游戏过程中,小明所处的坐标值依次为[0,−5,−3],最大坐标值为 0 。
解析
首先对每个参数m、n、n个指令进行一一校验。再通过for循环记录每次的位置,从中选出最大的位置。
答案
function getMaxCoordinate(str) {let arr = str.split('\n')let [n, m, instructs] = arrinstructs = instructs.split(' ').map(Number);// 参数校验if (n > 100 || n < 1 || 100 < m || m < -100 || instructs.length != n || instructs.some(v => !Number.isInteger(v))) {return 12345}let max = 0let cur = 0for (let i = 0; i < n; i++) {cur = instructs[i] == m ? cur + instructs[i] + 1 : cur + instructs[i]if (cur > max) {max = cur}}return max
}
console.log(getMaxCoordinate(`2
1
-5 1`))寻找最富裕的小家庭
考察深度优先、递归、hash
题目描述
在一棵树中,每个节点代表一个家庭成员,节点的数字表示其个人的财富值,
一个节点及其直接相连的子节点被定义为一个小家庭现给你一棵树,请计算出最富裕的小家庭的财富和。
输入描述
第一行为一个数N,表示成员总数,成员编号1-N,1<=N<=1000
第二行为N个空格分隔的数,表示编号1- N 的成员的财富值。 0 <= 财富值 <= 1000000
接下来 N-1 行,每行两个空格分隔的整数(N1,N2), 表示 N1 是 N2 的父节点
输出描述
最富裕的小家庭的财富和
示例1
输入
4
100 200 300 500
1 2
1 3
2 4
输出
700
说明

解析
首先通过哈希的key-value建立每个节点的联系,value代表当前节点的财富值,next表示他的直接子节点,pre表示父节点。
然后通过判断节点是否存在父节点来选出根节点,再从根节点开始通过深度优先遍历每个节点,计算每个节点当前的财富和,取出最大的财富和。
注意叶节点的财富和不可能大于父节点的财富和,所以可以过滤掉。
答案
function getMaxNum(str) {let arr = str.split('\n')let len = arr.shift()let nodes = arr.shift().split(' ').map(Number)let hash = {}arr.forEach(v => {v = v.split(' ')if (!hash[v[0]]) {hash[v[0]] = { value: nodes[v[0] - 1], next: [] }}if (!hash[v[1]]) {hash[v[1]] = { value: nodes[v[1] - 1], next: [] }}hash[v[0]].next.push(hash[v[1]])hash[v[1]].pre = hash[v[0]]})// 通过判断节点是否存在父节点来选出根节点let root = Object.values(hash).find(v => !v.pre)return bfs(root)}
function bfs(root, max = 0) {if (!root.next.length) {// 叶节点的财富和不可能大于父节点的财富和,所以可以过滤调return}// 计算当前节点的财富和let cur = root.value + root.next.reduce((t, v) => t + v.value, 0)if (cur > max) {max = cur}// 遍历子节点的财富和root.next.forEach(v => {let tmp = bfs(v, max)if (tmp > max) {max = tmp}})return max
}
console.log(getMaxNum(`4
100 200 300 500
1 2
1 3
2 4`))两个字符串间的最短路径问题
考察深度遍历、递归或动态规划。
题目描述
给定两个字符串,分别为字符串A与字符串B。例如A字符串为ABCABBA,B字符串为CBABAC。可以得到m*n的二维数组,
定义原点为(0,0),终点为(m,n),水平与垂直的每一条边距离为1,
从原点(0,0)到(0,A)为水平边,距离为1,从(0,A)到(A,C)为垂直边,距离为1;
假设两个字符串同一位置的两个字符相同则可以作一个斜边、如(A,C)到(B,B)最短距离为斜边,距离同样为1。
作出所有的斜边,则有(0,0)到(B,B)的距离为 1个水平边+1个垂直边+1个斜边=3。
根据定义可知,原点到终点的最短距离路径如下图红线标记,最短距离为9;
路径为(0,0)->(A,0)->(A,C)->(B,B)->(C,B)->(A,A)->(B,A)->(B,B)->(A,A)->(A,C)
输入描述
空格分割的两个字符串A与字符串B,字符串不为”空串”。
字符格式满足正则规则:[A-Z] 字符串长度<= 10000
输出描述
原点到终点的最短距离
示例1
输入
ABC ABC
输出
3
示例2
输入
ABCABBA CBABAC
输出
9
解析
方法一
使用深度遍历(递归)来查找最短路径。
我们用f(x,y)表示表示当前点x,y到终点的最短路径,首先需要找到f(x,y)和下一次的关系。每次走只能向右或者向下或者45度斜线,所以f(x,y)=Math.min(f(x+1,y),f(x,y+1),f(x+1,y+1))+1
需要判断什么情况下可以向右(x轴未到边界),向下(y轴未到边界),45度斜线(x+1,y+1对应的字母相同)。
找终点。
1.当x,y等于对应的终点点。
2.当当前步数已经超过了已经成功的最小步数。
方法二
使用动态规划来查找最短路径。
用二维数组arr[y][x]表示到0,0点的最短路径。
1.首先赋默认值当y等于0时,arr[0][x]=x,当x等于0时,arr[y][0]=y。
2.找到arr[y][x]和下一级的联系,即arr[y][x]=Math.min(arr[y-1][x],arr[y][x-1],arr[y-1][x-1])+1。其中arr[y-1][x-1]只有在x,y对应
的字母相同时出现。
答案
// 方法一深度遍历(递归)
function getMinPath(str){let [x,y] = str.split(' ')x = x.split('')y = y.split('')let endx = x.lengthlet endy = y.lengthreturn bfs(0,0,endx,endy,x,y)
}
function bfs(curx,cury,endx,endy,x,y,min=Infinity,step=0){if(curx===endx&&cury===endy){// 到达终点return step}if(step>=min){// 已走步数大于已经成功的最小值return}let tmpif(x[curx]===y[cury]){// 45度向下走tmp = bfs(curx+1,cury+1,endx,endy,x,y,min,step+1)if(tmp<min){min = tmp}}if(curx<endx){// 向右走一步tmp = bfs(curx+1,cury,endx,endy,x,y,min,step+1)if(tmp<min){min = tmp}}if(cury<endy){// 向下走一步tmp = bfs(curx,cury+1,endx,endy,x,y,min,step+1)if(tmp<min){min = tmp}}return min
}
// 方法二动态规划
function getMinPath(str){let [x,y] = str.split(' ')x = x.split('')y = y.split('')let endx = x.lengthlet endy = y.lengthlet pathArr = new Array(endy+1).fill(0).map(v=>new Array(endx+1).fill(0))pathArr[0]=pathArr[0].map((v,i)=>i)for(let i = 0;i<=endy;i++){pathArr[i][0]=i}for(let i=1;i<=endy;i++){for(let j=1;j<=endx;j++){if(y[i-1]===x[j-1]){pathArr[i][j]=Math.min(pathArr[i-1][j],pathArr[i][j-1],pathArr[i-1][j-1])+1}else{pathArr[i][j]=Math.min(pathArr[i-1][j],pathArr[i][j-1])+1}}}return pathArr[endy][endx]
}
console.log(getMinPath(`ABC ABC`))
console.log(getMinPath(`ABCABBA CBABAC`))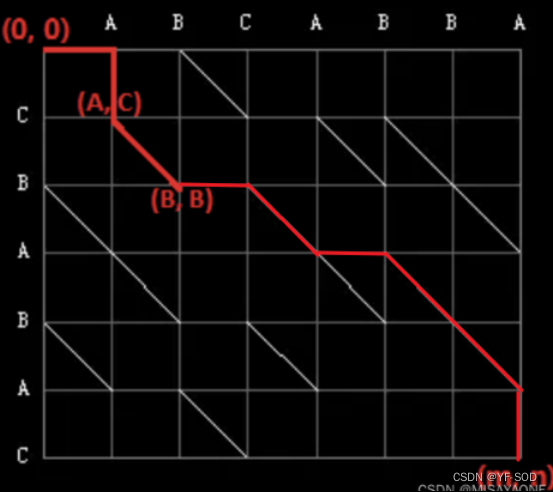



![CLion2024 for Mac[po] C和C++的跨平台解代码编辑器](https://img-blog.csdnimg.cn/direct/17479a8bf98348d98d9d82f478edba5a.png)