个人主页:C++忠实粉丝
欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 C++忠实粉丝 原创排序之插入排序----直接插入排序和希尔排序(1)
收录于专栏【数据结构初阶】
本专栏旨在分享学习数据结构学习的一点学习笔记,欢迎大家在评论区交流讨论💌
目录
1.排序的概念及其运用
1.1排序的概念
1.2排序运用
1.2.1 购物和电商
1.2.2 图书馆和书店
1.2.3 教育
1.2.4 交通和物流
1.2.5 餐饮业
1.3 常见的排序算法
2.插入排序
2.1基本思想
2.2直接插入排序
2.2.1直接插入排序的概念:
2.2.2直接插入排序示例:
2.2.3动图演示:
2.2.4代码实现:
2.2.5测试代码:
2.2.6时间复杂度分析
2.3希尔排序 ( 缩小增量排序 )
2.3.1希尔排序的概念
2.3.2希尔排序图解分析:
2.3.3代码展示:
2.3.4测试代码:
2.3.5希尔排序时间复杂分析:
2.3.6 希尔排序的特性总结:
2.4希尔排序与直接插入排序的关系和比较
3总结
1.排序的概念及其运用
1.1排序的概念
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次 序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排 序算法是稳定的;否则称为不稳定的。
内部排序:数据元素全部放在内存中的排序。
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不断地在内外存之间移动数据的排序。
1.2排序运用
排序算法在生活中有着广泛的应用,无论是日常活动还是专业领域,都能看到排序算法的身影。以下是一些具体的例子:
1.2.1 购物和电商
- 产品排列:在线购物平台会根据价格、销量、评价等对商品进行排序,方便用户查找和比较。
- 推荐系统:根据用户的浏览和购买历史,推荐系统会对可能感兴趣的商品进行排序。
1.2.2 图书馆和书店
- 分类与索引:图书按字母顺序、类别、作者或者出版日期排序,方便读者查找。
- 借阅记录:按时间顺序记录借还书信息,便于管理和统计。
1.2.3 教育
- 成绩排名:考试成绩会按照分数排序,以便评估学生的表现。
- 学籍管理:按学号或姓名排序学生信息,便于查询和管理。
1.2.4 交通和物流
- 航班和列车时刻表:按出发时间、目的地等排序,方便乘客查询和安排行程。
- 快递分拣:按目的地、优先级等对包裹进行排序,提高运送效率。
1.2.5 餐饮业
- 菜单排序:餐厅菜单按菜品类型、受欢迎程度等排序,方便顾客选择。
- 订单处理:按下单时间、优先级等排序订单,确保及时准确地完成服务。
这些例子展示了排序算法在各种场景中的重要性和广泛应用,从而提高了效率和用户体验。无论是简单的字母排序还是复杂的多条件排序,排序算法在现代生活中都是不可或缺的工具。
1.3 常见的排序算法
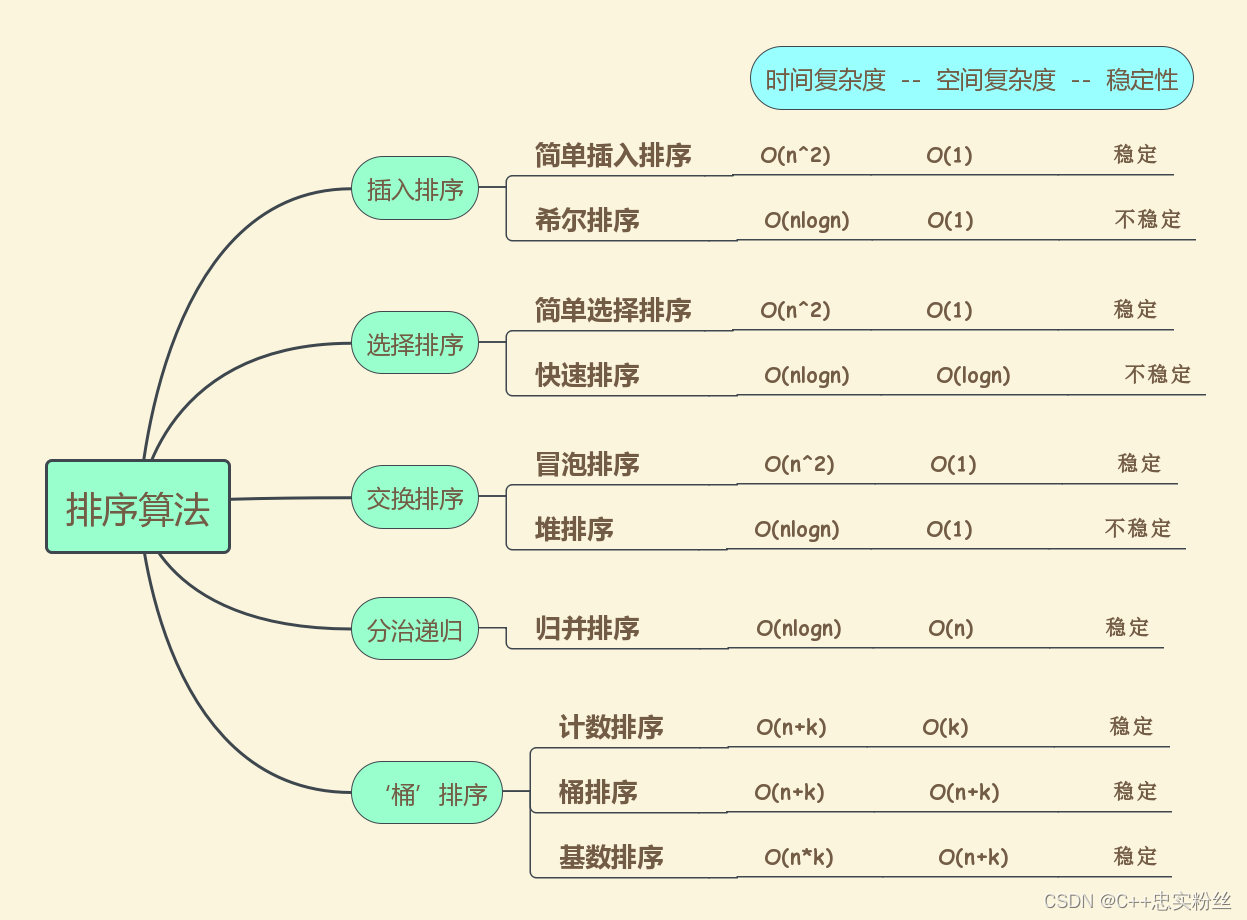
大家可以去下面链接查看各个排序算法的动态演示效果
--Comparison Sorting Visualization (usfca.edu)
2.插入排序
2.1基本思想
直接插入排序是一种简单的插入排序法,其基本思想是: 把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。
实际中我们玩扑克牌时,就用了插入排序的思想
2.2直接插入排序
2.2.1直接插入排序的概念:
直接插入排序(Insertion Sort)是一种简单直观的排序算法,其基本思想是逐步构建有序序列。具体操作如下:
初始状态:将序列分为两部分,一部分是有序序列,初始时只包含第一个元素;另一部分是无序序列,包含剩余的元素。
排序过程:
- 从第二个元素开始,依次将该元素插入到前面已经排好序的序列中的合适位置。
- 假设当前要插入的元素为
current_value,将current_value与已排序序列中的元素从后向前逐个比较。- 如果发现已排序元素比
current_value大,则将该元素后移一位,直到找到比current_value小的位置,或者到达序列的开头。- 将
current_value插入到找到的位置后,此时已排序序列长度增加一。重复:重复以上步骤,直到所有元素都插入到有序序列中。
结束:当所有元素都插入到有序序列后,排序完成。
2.2.2直接插入排序示例:
假设要对数组 [5, 2, 4, 6, 1, 3] 进行直接插入排序:
- 初始时,有序序列为
[5],无序序列为[2, 4, 6, 1, 3]。 - 将
2插入到[5]中,得到[2, 5],无序序列变为[4, 6, 1, 3]。 - 将
4插入到[2, 5]中,得到[2, 4, 5],无序序列变为[6, 1, 3]。 - 依此类推,直到所有元素都插入到有序序列中,最终得到排序后的数组
[1, 2, 3, 4, 5, 6]。
直接插入排序虽然简单,但在某些特定情况下仍然可以提供不错的性能,特别是在处理部分有序的数据或者数据量较小时。
2.2.3动图演示:
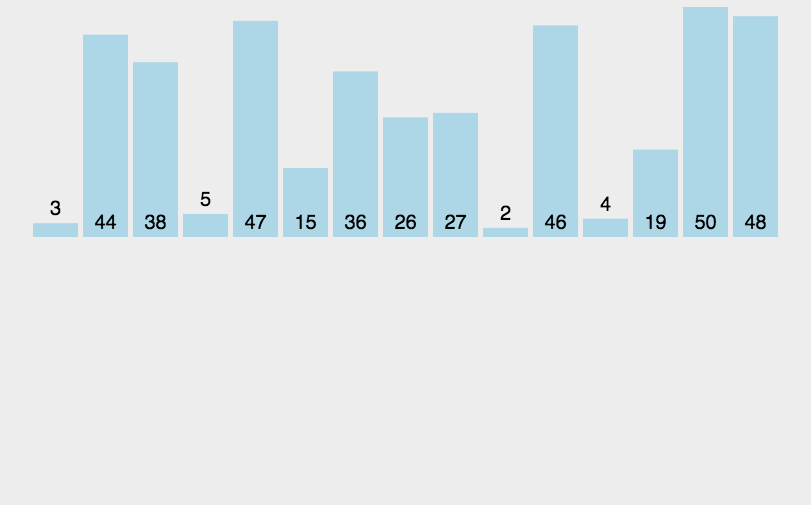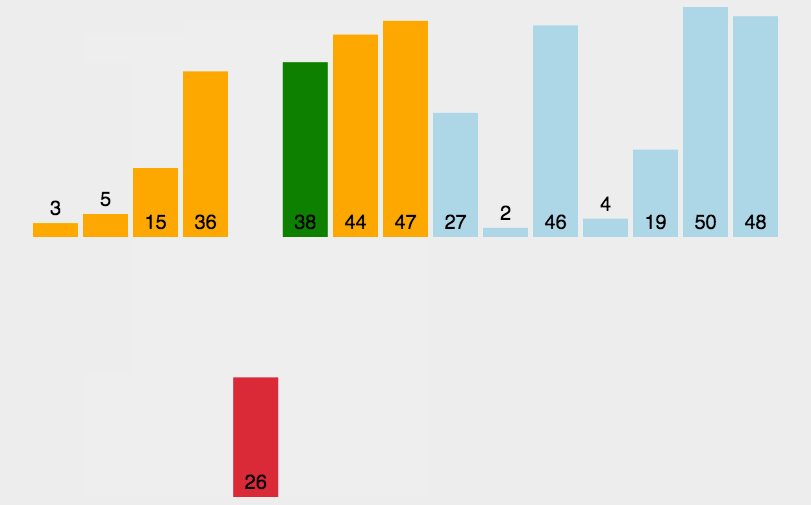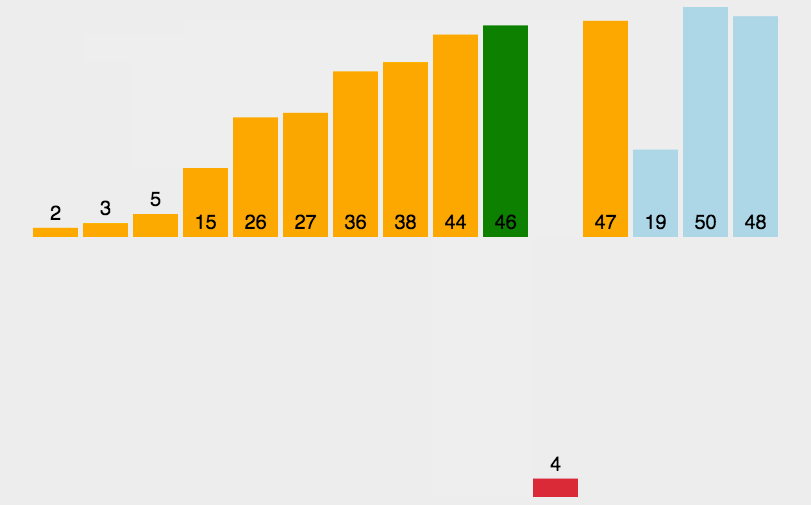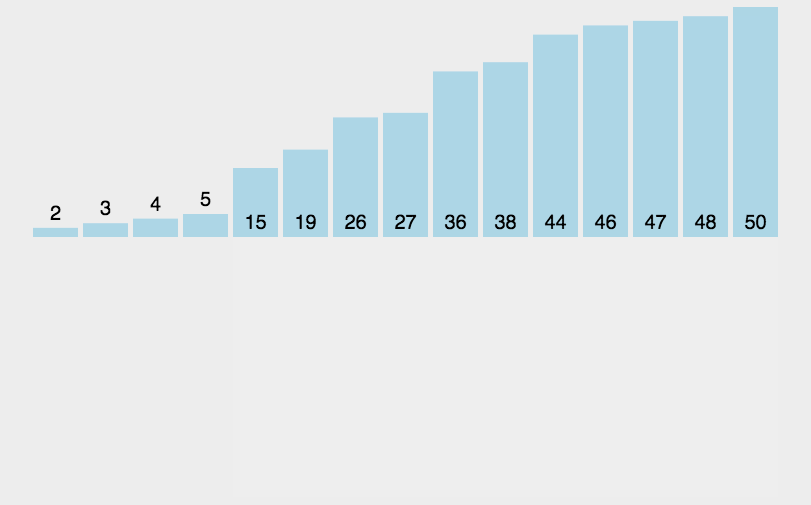
2.2.4代码实现:
void InsertSort(int* a, int n)
{// [0, n-1]for (int i = 0; i < n - 1; i++){// [0, n-2]是最后一组// [0,end]有序 end+1位置的值插入[0,end],保持有序int end = i;int tmp = a[end + 1];while (end >= 0){if (tmp < a[end]){a[end + 1] = a[end];--end;}else{break;}}a[end + 1] = tmp;}
}分析:
外层循环(i 循环):
for (int i = 0; i < n - 1; i++)循环遍历数组,从第一个元素到倒数第二个元素。每次迭代开始时,数组从a[0]到a[i]是已经排好序的部分。内层循环(end 循环):
int end = i;将当前元素a[i+1]视为待插入的元素。int tmp = a[end + 1];记录待插入元素的值。插入过程:
while (end >= 0)内层循环用于找到待插入元素tmp的正确位置。if (tmp < a[end])如果待插入元素比当前位置a[end]的元素小,则将a[end]向后移动一位,即a[end + 1] = a[end];,同时end--继续向前比较。- 当找到合适的位置(即
tmp >= a[end]),退出内层循环。插入操作:
a[end + 1] = tmp;将tmp插入到找到的合适位置end + 1处,此时数组从a[0]到a[i+1]又变成有序状态。注意:我们的外层循环
for (int i = 0; i < n - 1; i++)是遍历的是我们已经排好序的数组,我们需要排的数为a[end+1],也就是a[i+1],所以这里i<n-1,不能等于n-1
2.2.5测试代码:
测试链接:912. 排序数组 - 力扣(LeetCode)
题目描述:
给你一个整数数组 nums,请你将该数组升序排列。
示例 1:
输入:nums = [5,2,3,1] 输出:[1,2,3,5]
示例 2:
输入:nums = [5,1,1,2,0,0] 输出:[0,0,1,1,2,5]
提示:
1 <= nums.length <= 5 * 104-5 * 104 <= nums[i] <= 5 * 104
代码展示:
void InsertSort(int* a, int n)
{for(int i = 0; i < n-1; i++){int end = i;int tmp = a[end + 1];while(end >= 0){if(a[end] > tmp){a[end + 1] = a[end];end--;}else{break;}}a[end + 1] = tmp;}
}int* sortArray(int* nums, int numsSize, int* returnSize) {(*returnSize) = numsSize;int* array = (int*)malloc(sizeof(int)*(*returnSize));for(int i = 0; i < numsSize; i++){array[i] = nums[i];}InsertSort(array, numsSize);return array;
}2.2.6时间复杂度分析
插入排序可以说是排序的最底层,它最好的情况是有序,时间复杂度为O(n),很显然这种情况很少见,最坏的情况是逆序,时间复杂度为O(n^2).在平均情况下,直接插入排序的时间复杂度也是 O(n^2)。虽然有时候可能会比较少于最坏情况下的比较次数,但是对于大规模的随机数组,其平均时间复杂度仍然是二次阶的。
在力扣这道题目中只通过了12个例子就超时了.....
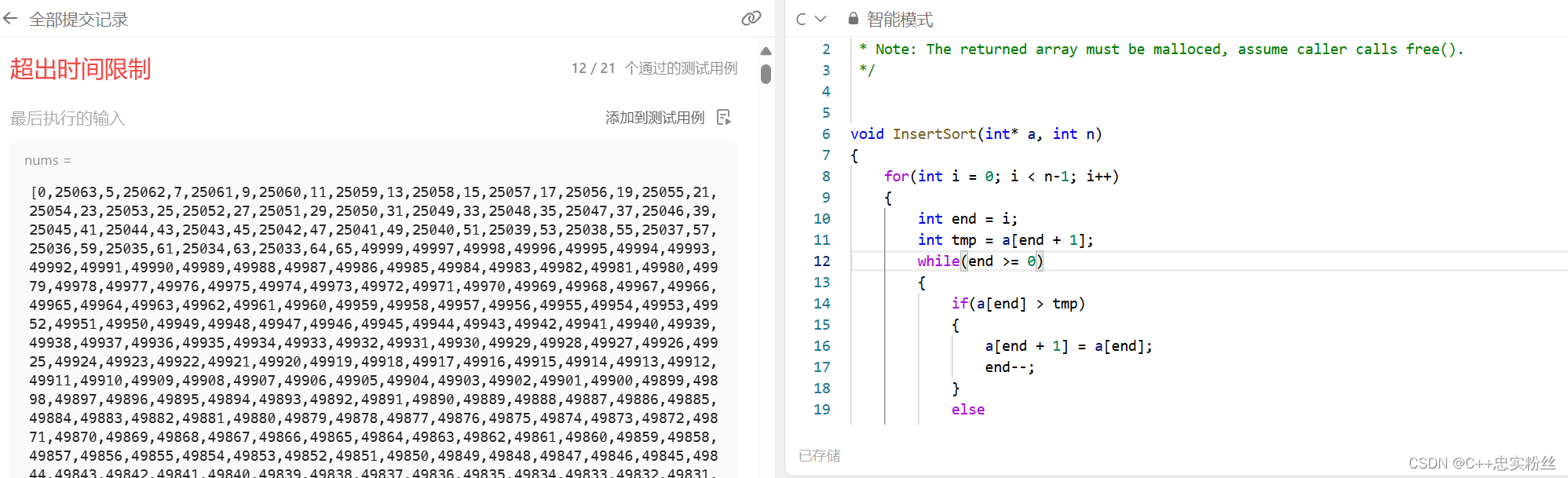
直接插入排序的特性总结:
1. 元素集合越接近有序,直接插入排序算法的时间效率越高
2. 时间复杂度:O(N^2)
3. 空间复杂度:O(1),它是一种稳定的排序算法
4. 稳定性:稳定
2.3希尔排序 ( 缩小增量排序 )
2.3.1希尔排序的概念
希尔排序(Shell Sort)是一种改进的插入排序算法,也称作缩小增量排序。希尔排序通过将原始序列分割成若干个子序列来改善插入排序的性能,每个子序列分别进行插入排序,最后再对整体进行一次插入排序。其基本思想可以描述如下:
步骤:
- 选择一个增量序列,通常是使用 Knuth 序列(例如 ( n / 2, n / 4, ..., 1 ))或者 Hibbard 序列(( 2^k - 1 ))来作为增量。
- 根据选定的增量序列,将待排序的序列分割成若干个子序列。
- 对每个子序列分别进行插入排序。
- 逐渐缩小增量,重复以上步骤,直到增量为 1。
排序过程:
- 假设待排序数组为
[5, 2, 4, 6, 1, 3]。- 如果选取增量序列为 ( n / 2, n / 4, ..., 1 ),则初始增量 ( n / 2 = 3 )。
- 分别对
[5, 6]、[2, 1]、[4, 3]这三个子序列进行插入排序。- 第一次插入排序后,可能得到
[1, 2, 3, 5, 4, 6]。- 接下来使用更小的增量进行插入排序,直到最终使用增量为 1 的插入排序完成整体排序。
2.3.2希尔排序图解分析:
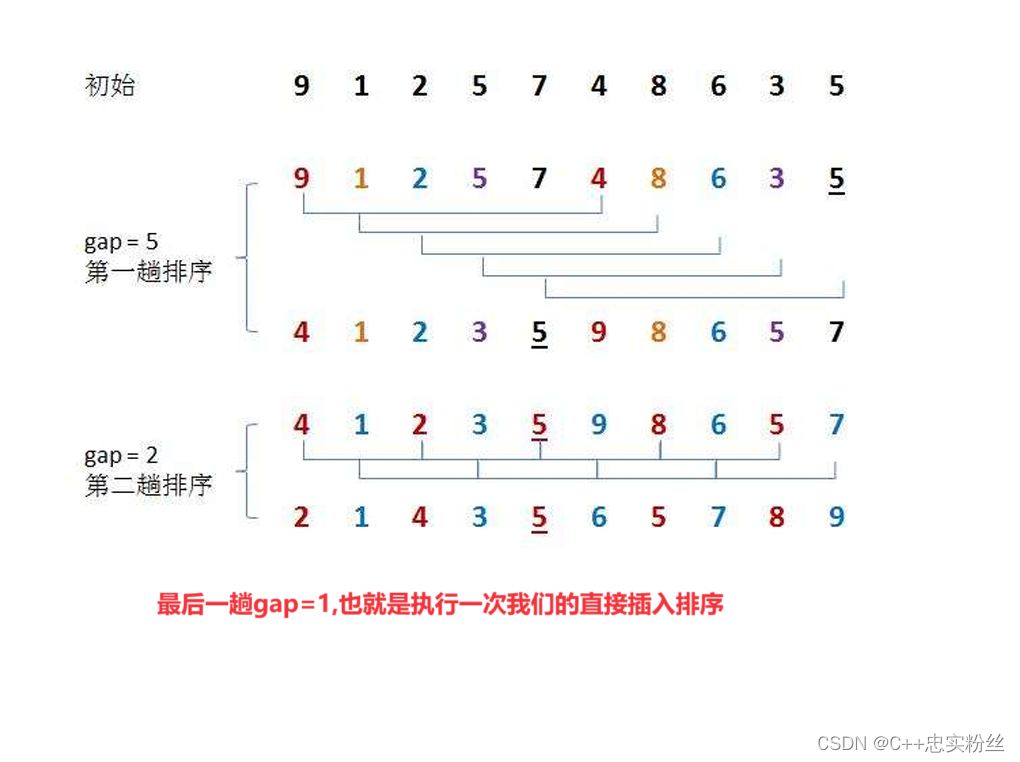
2.3.3代码展示:
void ShellSort(int* a, int n)
{int gap = n;while (gap > 1){// +1保证最后一个gap一定是1// gap > 1时是预排序// gap == 1时是插入排序gap = gap / 3 + 1;for (size_t i = 0; i < n - gap; ++i){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}
}
代码逻辑:
初始设置 gap:
- 初始时,将 gap 设置为数组长度 n。在每一轮迭代中,通过
gap = gap / 3 + 1逐渐减小 gap 的值,直到最后一次迭代时 gap 等于 1,变成普通的插入排序。主循环(while 循环):
- 当 gap 大于 1 时,进行希尔排序的预处理阶段,即根据当前的 gap 进行分组预排序。
- 当 gap 等于 1 时,执行最后一轮,此时相当于执行普通的插入排序。
预排序阶段:
- 对于每个 gap 值,通过一个 for 循环遍历数组,对每个分组进行插入排序。这里的
for (size_t i = 0; i < n - gap; ++i)控制每个分组的起始位置。插入排序:
- 对于当前的分组起始位置 i,使用插入排序的方式将该分组内的元素排序。
- 内部的 while 循环用于找到合适的插入位置,确保当前位置的元素插入到正确的位置。
交换和移动:
- 如果当前位置的元素比 tmp(待插入元素)大,则将当前位置的元素向后移动 gap 个位置,直到找到合适的插入位置。
- 插入位置确定后,将 tmp 插入到该位置。
最终结果:
- 经过多次循环和逐步缩小的 gap 值处理后,数组 a 将被排序完成。
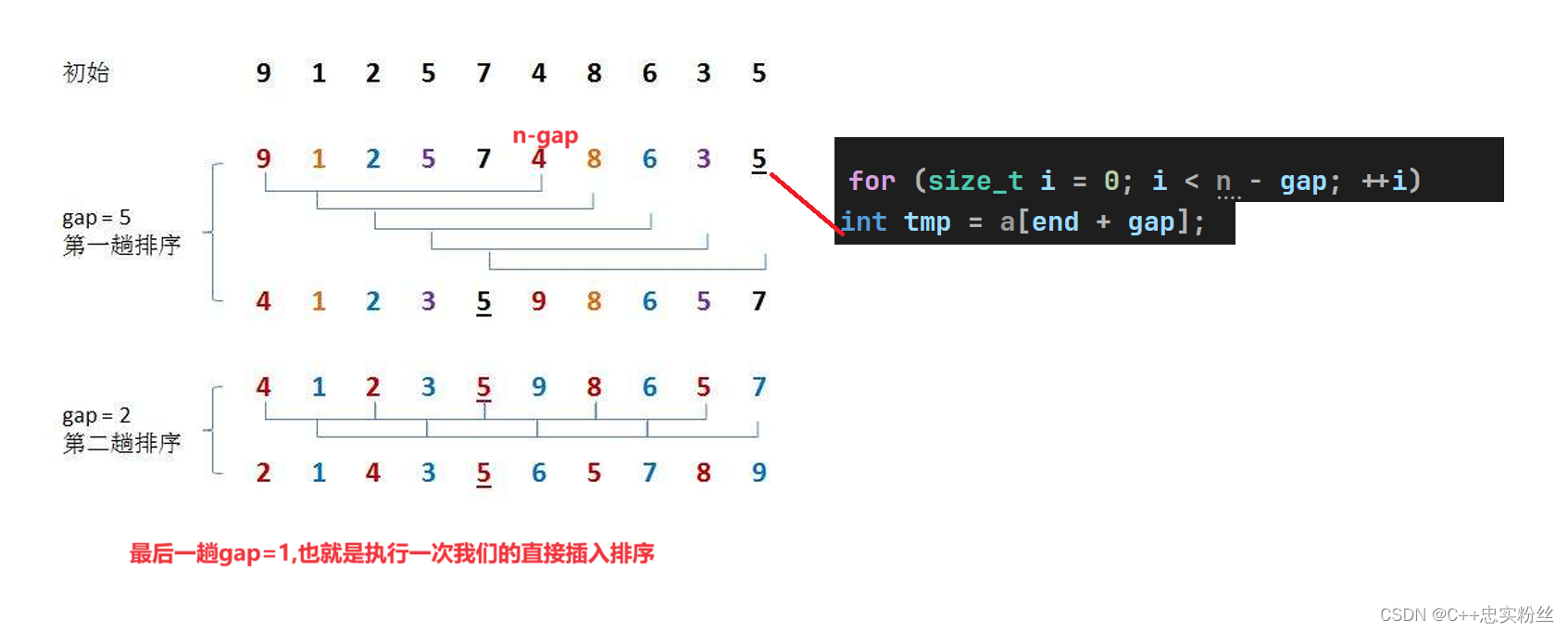
2.3.4测试代码:
测试链接:912. 排序数组 - 力扣(LeetCode)
代码展示:
void ShellSort(int* a, int n)
{int gap = n;while(gap > 1){gap = gap/3 + 1;for(int i = 0; i < n - gap; i++){int end = i;int tmp = a[end + gap];while(end >= 0){if(tmp < a[end]){a[end + gap] = a[end];end-=gap;}else{break;}}a[end + gap] = tmp;}}
}int* sortArray(int* nums, int numsSize, int* returnSize) {(*returnSize) = numsSize;int* array = (int*)malloc(sizeof(int)*(*returnSize));for(int i = 0; i < numsSize; i++){array[i] = nums[i];}ShellSort(array, numsSize);return array;
}结果展示:
居然过了!!!!!!!!!!
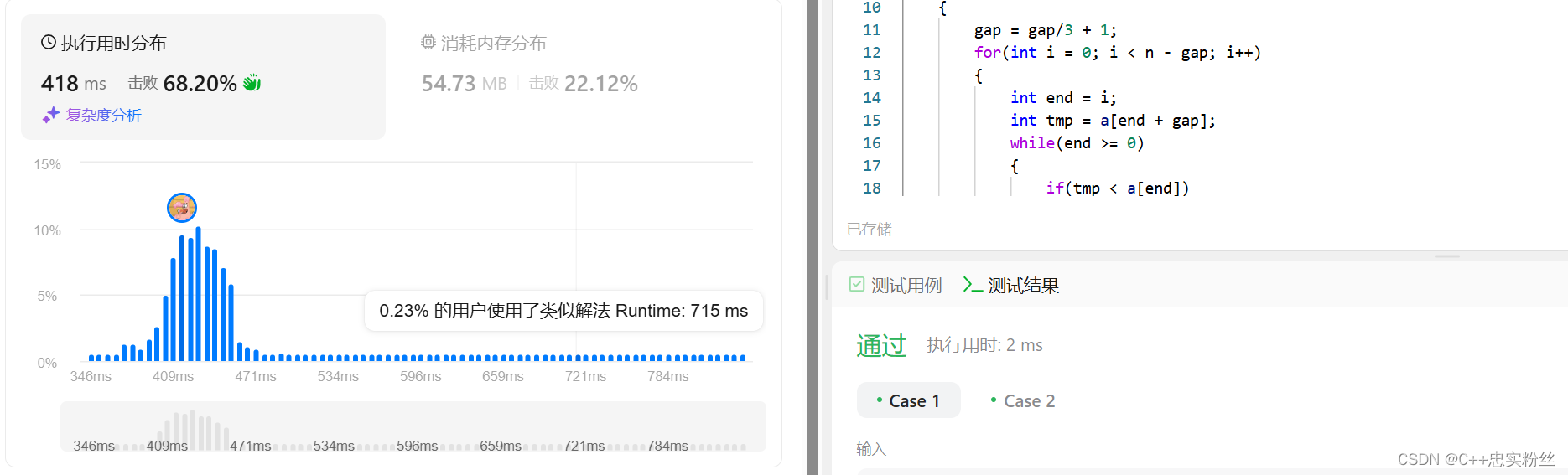
希尔排序虽然有点难理解,看起来很复杂,但是它的效率真的很高.
2.3.5希尔排序时间复杂分析:
有关希尔排序的时间复杂度至今都没有定论.

《数据结构(C语言版)》--- 严蔚敏

《数据结构-用面相对象方法与C++描述》--- 殷人昆
因为我的gap是按照Knuth提出的方式取值的,而且Knuth进行了大量的试验统计,我们暂时就按照:O(n^1.3)来算
那为什么希尔排序的时间复杂难算呢?
第一次预排序 gap = n/3(这里我们将-1省略方便计算),一组有3个数据(n=10),最坏的情况需要排3次,也就是3*3/n=n,也就是说,希尔第一次预排序接近于O(n)
最后一次排序:数组接近有序,可以看成O(n)
第二次预排序:gap=n/9,每组九个数据,最坏的情况(1+2.....+8)*n/9=4n
注意:这里我们第二次预排序取得是最坏的情况,而经过我们第一次得预排序,我们第二次往往不会是最坏的情况,希尔排序难就难在除第一次和最后一次,其他情况是变化的
2.3.6 希尔排序的特性总结:
1. 希尔排序是对直接插入排序的优化。
2. 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就 会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。
3. 希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算,因此在好些树中给出的 希尔排序的时间复杂度都不固定:
2.4希尔排序与直接插入排序的关系和比较
关系与比较:
基础原理: 希尔排序可以看作是对直接插入排序的改进,通过预处理数据,使其更接近最终排序后的位置,从而减少了直接插入排序中的元素比较和移动次数。
性能比较: 在数据量较小时,直接插入排序可能会比希尔排序更快,因为希尔排序的预处理阶段可能带来一定的额外开销。但是在大规模数据和随机数据排序时,希尔排序通常能够明显优于直接插入排序。
稳定性: 直接插入排序是稳定的,而希尔排序一般来说是不稳定的,这是因为希尔排序涉及多个子序列的插入排序,子序列之间的相对顺序可能发生变化。
综上所述,希尔排序和直接插入排序虽然在实现上有所区别,但它们的基本思想都是通过逐步将元素移动到正确位置来完成排序,希尔排序通过增量序列的方式优化了插入排序的性能,特别是在处理大规模数据时表现更为优越。
3总结
直接插入排序和希尔排序虽然在我们排序中使用较少,但它们具有可使用性,尤其是希尔排序(从它AC力扣的数组排序就可以看出)
我马上会更选择排序--(选择排序和推排序)
宝子们记得点赞关注支持一下
我将会在数据结构初阶这个专栏持续更新

![NSSCTF中的[WUSTCTF 2020]朴实无华、[FSCTF 2023]源码!启动! 、[LitCTF 2023]Flag点击就送! 以及相关知识点](https://img-blog.csdnimg.cn/direct/8380c8c294a04b508433106b944e5411.png)