什么是布隆过滤器
它实际上是一个很长的二进制向量和一系列随机映射函数。布隆过滤器可以用于检索一个元素是否在一个集合中。它的优点是空间效率和查询时间都比一般的算法要好的多,缺点是有一定的误识别率和删除困难。主要用于判断一个元素是否在一个集合中。
布隆过滤器的优点:
- 支持海量数据场景下高效判断元素是否存在
- 布隆过滤器存储空间小,并且节省空间,不存储数据本身,仅存储hash结果取模运算后的位标记
- 不存储数据本身,比较适合某些保密场景
布隆过滤器的缺点:
- 不存储数据本身,所以只能添加但不可删除,因为删掉元素会导致误判率增加。
- 由于存在hash碰撞,匹配结果如果是“存在于过滤器中”,实际不一定存在
- 当容量快满时,hash碰撞的概率变大,插入、查询的错误率也就随之增加了
布隆过滤器中一个元素如果判断结果为存在的时候元素不一定存在,但是判断结果为不存在的时候则一定不存在。因此,布隆过滤器不适合那些对结果必须精准的应用场景。
布隆过滤器适合的场景
- 预防缓存穿透:布隆过滤器快速判断数据是否存在,避免通过查询数据库来判断数据是否存在。
- 网络爬虫:布隆过滤器可以用来去重已经爬取过的URL。
- 邮箱的垃圾邮件过滤。
- 黑白名单。
布隆过滤器原理
数据结构
布隆过滤器是由一个固定大小的二进制向量或者位图(bitmap)和一系列映射函数组成的。
对于长度为 m 的位数组,在初始状态时,它所有位置都被置为0,如下图所示:
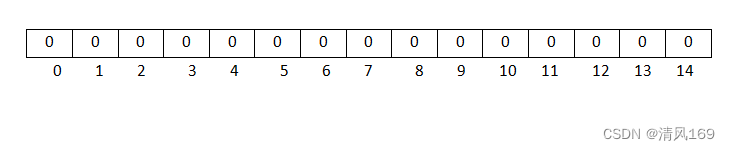
位数组中的每个元素都只占用 1 bit ,并且数组中元素只能是 0 或者 1。这样申请一个 100w 个元素的位数组只占用 1000000Bit / 8 = 125000 Byte = 125000/1024 KB ≈ 122KB 的空间。
增加元素
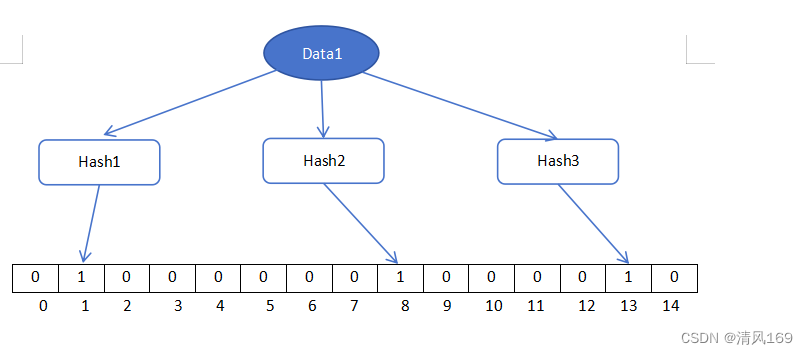
将要添加的元素分别通过k个哈希函数计算得到k个哈希值,这k个hash值对应位数组上的k个位置,然后将这k个位置设置为1。这里的k为3,分别为Hash1、Hash2、Hash1。
我们添加一个data1和data2两个元素,两个元素根据三个hash算法函数计算出的值,需要说明一点三个值可能会存在相同的值。
其中data1计算出1、8、13三值,我们把数组中对应的位置设置为1。
Hash1(data1)=1
Hash2(data1)=8
Hash3(data1)=13
data2计算出2、5、13三值,我们把数组中对应的位置设置为1
Hash1(data2)=2
Hash2(data2)=5
Hash3(data2)=13

我们发现data1和data2经过hash函数后,出现了一个相同值(13),这种是正常的,也正是因为这种情况的存在,需要多个函数来保证每个元素尽可能对应数组位置的唯一性。
查询元素
将要查询的元素分别通过k个哈希函数计算得到k个哈希值,这k个hash值对应位数组上的k个位置。如果这k个位置中有一个位置为0,则此元素一定不存在集合中。如果这k个位置全部为1,则这个元素可能存在。
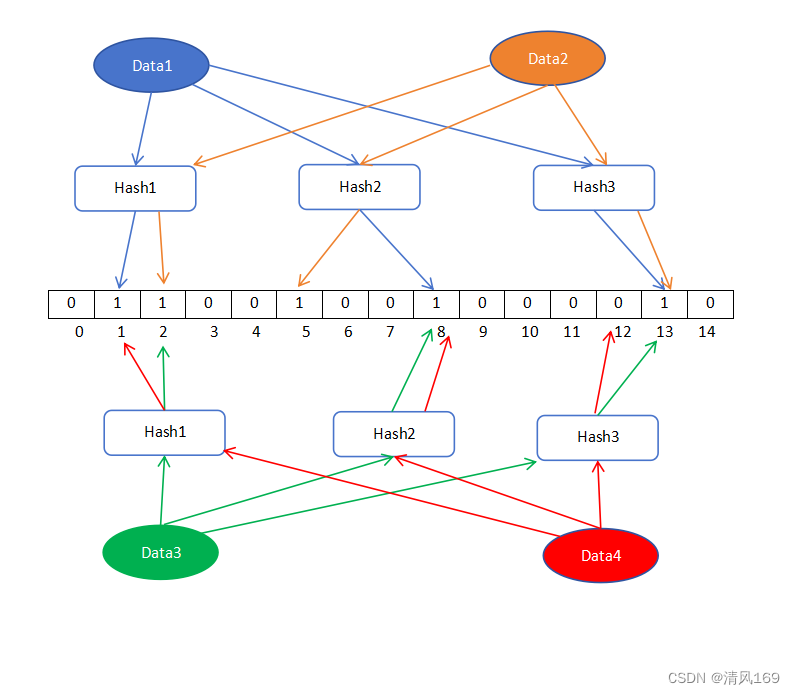
刚才添加过data1和data2两个元素,而data3和data4都是未添加到布隆过滤器的元素。
查询data1先根据添加时的三个hash函数计算分别对应值,值分别是1、8、13,这三个位置都是1,data1可能存在于该布隆过滤器。我们从添加的角度来看,我们知道data1是一定存在于该布隆过滤器的,为什么还要是说可能呢,是因为查询出来三个位置都为1不能代表这个三个1都是同一个元素添加的,下面我们看下元素data3的查询。
查询data3先根据添加时的三个hash函数计算分别对应值,值分别是2、8、13,然后查询数组中这三个位置的值是否为1。
Hash1(data3)=2
Hash2(data3)=8
Hash3(data3)=13
我们已知的该布隆过滤器我们没有添加给data3,为什么data3查询出来三个位置的值都为1呢。我们可以看到data3所命中的位置分别是data2添加时把位置2赋值的1,data1添加时把位置8和位置13赋值的1,都是由其他元素改变的位置对应的值,所以命中位置全部为1。
我们查询一下data4,
Hash1(data4)=1
Hash2(data4)=8
Hash3(data4)=12
我们可以看到data4元素的hash函数3计算之后的值是12,数组位置12的值是0,没有元素在位置12赋值过1。如果data4存在于该布隆过滤器,则一定在添加data4时会把位置12赋值1,此时位置12还是0,则说明该布隆过滤器未添加过data4元素,所有位置中有一个位置为0。则此元素一定不存在布隆过滤器中。
布隆过滤器误判率
m:布隆过滤器的bit长度。
n:插入过滤器的元素个数。
k:哈希函数的个数。
p:误差率
推导过程(可忽略)


误判率公式
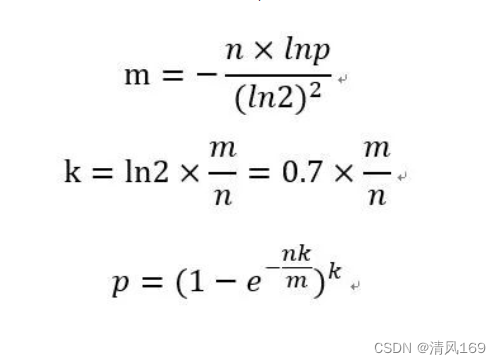
实用参考网址:
https://hur.st/bloomfilter/
https://pages.cs.wisc.edu/~cao/papers/summary-cache/node8.html
实际案例
现在有个100亿个黑名单网页数据,每个网页的URL占用64字节。现在想要实现一种网页过滤系统,可以根据网页的URL判断该网站是否在黑名单上,请设计该系统。
要求:可以允许有0.01%以下的判断失误率,并且使用的总空间不要超过30G。
要将100亿个64字节的数据转换为GB(gigabytes),我们需要进行以下计算:1. 首先,将100亿个64字节的数据转换为字节:100亿 * 64字节 = 6400亿字节2. 然后,将字节转换为GB:1 GB = 1024 MB = 1024 * 1024 KB = 1024 * 1024 * 1024 字节因此,6400亿字节 = 6400亿 ÷ (1024 * 1024 * 1024) GB3. 进行计算:6400亿 ÷ 1073741824 ≈ 596.05 GB因此,100亿个64字节的数据约等于596.05 GB。
以下是详细的设计方案:
- 布隆过滤器设计:
a. 确定位数组大小(m):
假设我们希望误判率为0.01%(即0.0001)
使用公式:
其中 n=10000000000(100亿),p=0.0001(0.01%的误判率)m = -(n * ln(p)) / (ln(2)^2)
计算得: m ≈ 191702989335 bits ≈ 22.31 GB
b. 确定哈希函数数量(k):
使用公式: k = (m/n) * ln(2)
计算得: k ≈ 14
通过布隆过滤器公式也可以看出:
单个数据的大小不影响布隆过滤器大小,因为样本会通过哈希函数得到输出值。
就好比上面的 每个网页的URL占用64字节 这个数据大小 跟布隆过滤器大小没啥关系。