概率论论文(关于“到课率”的贝叶斯推理应用)
全条件概率公式和贝叶斯公式趣味识
思考1: (引自贝叶斯公式及朴素贝叶斯分类算法应用初探)
“狼来了”的故事想必大家都知道,小孩子第三次对村民说狼来了的时候,村民们没有相信他的话,从而酿成小孩子被狼吃掉的结局,这个故事告诉我们做人要诚信。小时候,我们都能感性地认识到随着小孩子撒谎次数增加,村民对小孩子越来越不信任了,但村民对小孩子的信任度如何用理性的数学来刻画,让我们从更深层次理解小孩子的结局呢?
解答:设事件A表示小孩子说谎,事件B1表示小孩子可信,B2表示小孩子不可信。
由于本问题是实际问题,我们做如下假设:假设开始村民对小孩子的信任度为0.8,即P(B)=0.8,假设可信的小孩子说谎的概率为0.1,即P(A|B1)=0.1,不可信的小孩子说谎的概率为0.5,即P(A|B2)=0.5
要使用贝叶斯公式计算村民对小孩子的信任度,我们需要知道几个条件概率和先验概率。贝叶斯公式如下:
P(B|A) = P(A|B) * P(B) / P(A)
其中:
P(B|A) 是在已知小孩子说谎(事件A)的情况下,小孩子是可信的(事件B1)后验概率。
P(A|B) 是在已知小孩子可信的情况下,他说谎的条件概率。
P(B) 是小孩子可信的先验概率。
P(A) 是小孩子说谎的总概率,可以通过全概率公式计算得出。
首先,我们假设开始时村民对小孩子的信任度为0.8,即P(B1) = 0.8,那么小孩子不可信的概率P(B2) = 1 - P(B1) = 0.2。第一次小孩子说谎后,我们使用贝叶斯公式计算村民对小孩子的信任度:
P(B1|A) = P(A|B1) * P(B1) / P(A)
我们需要计算P(A),即小孩子说谎的总概率,可以使用全概率公式:
P(A) = P(A|B1) * P(B1) + P(A|B2) * P(B2)
= 0.1 * 0.8 + 0.5 * 0.2
= 0.08 + 0.1
= 0.18现在我们可以计算P(B1|A):
P(B1|A) = P(A|B1) * P(B1) / P(A)
= 0.1 * 0.8 / 0.18
= 0.08 / 0.18
≈ 0.44这意味着在第一次小孩子说谎后,村民对小孩子的信任度下降到了大约0.44。
第二次小孩子又说了谎,我们再次使用贝叶斯公式计算村民对小孩子的信任度:
P(B1|A) = P(A|B1) * P(B1|A) / P(A)
我们已经知道P(B1|A) ≈ 0.44,所以P(B1) = P(B1|A),因为这是新的先验概率。我们需要重新计算P(A):
P(A) = P(A|B1) * P(B1|A) + P(A|B2) * P(B2|A)
= 0.1 * 0.44 + 0.5 * (1 - 0.44)
= 0.044 + 0.5 * 0.56
= 0.044 + 0.28
≈ 0.324现在我们可以计算P(B1|A):
P(B1|A) = P(A|B1) * P(B1|A) / P(A)
= 0.1 * 0.44 / 0.324
≈ 0.1358这意味着在第二次小孩子说谎后,村民对小孩子的信任度进一步下降到了大约0.1358。
这个结果表明,经过两次说谎之后,村民对小孩子的信任度显著下降,他们更不可能相信小孩子第三次说狼来了的话。这就是为什么小孩子最终没有得到帮助的原因。
思考二:
假设在电子科技大学某学期体检中,男生在一个体检室,女生在一个体检室,由于效率有限,你作为一个男生排在浩浩荡荡的男生体检室门口的队伍里。突然,你眼前一亮,前方有一个长发“小姐姐”?不,实际上你并不知道是他还是她,但是排队实在无聊,如果是长发小姐姐的话,你正在预谋这一场搭讪,虽然她极有可能是正在等待她男朋友。那么,你将应用概率论的知识进行一场贝叶斯推理(靠常识和背景知识判断之外的数学实现方式,以实现更精准的预测)来决定是否要去搭讪。
解答:由于是在男生体检室门前,我们假设有100人正在门口等候,其中98个男生,2个是女生,正在等待其男朋友。假设女生中长发、短发人数之比为1:1,男生中短发与长发之比为24:1,记男生体检室门口,女生出现的事件为A1,男生出现的事件为A2,某个人是长发的事件为B,根据假设,则有P(B|A1)=0.5,P(B|A2)=0.04,P(A1)=0.02,P(A2)=0.98.
首先,我们需要计算在男生体检室门口遇到长发小姐姐的概率。根据题目中给出的信息,我们可以使用贝叶斯定理来进行计算。
贝叶斯定理的公式是:
P ( A ∣ B ) = P ( B ∣ A ) ⋅ P ( A ) P ( B ) P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)} P(A∣B)=P(B)P(B∣A)⋅P(A)
其中:
- P(A|B) 是在已知某人是长发的情况下,这个人是女生的条件概率。
- P(B|A) 是在已知某人是女生的情况下,这个人是长发的条件概率。
- P(A) 是随机选中的人是女生的先验概率。
- P(B) 是随机选中的人是长发的总概率。
根据题目中的信息,我们有:
- P(B|A1) = 0.5 (女生中长发的比例)
- P(B|A2) = 0.04 (男生中长发的比例)
- P(A1) = 0.02 (女生在队伍中的比例)
- P(A2) = 0.98 (男生在队伍中的比例)
我们可以计算出长发的人是女生的概率 P(A1|B) :
P ( A 1 ∣ B ) = P ( B ∣ A 1 ) ⋅ P ( A 1 ) P ( B ) P(A1|B) = \frac{P(B|A1) \cdot P(A1)}{P(B)} P(A1∣B)=P(B)P(B∣A1)⋅P(A1)
首先计算 P(B) ,即随机选中的人是长发的总概率:
P ( B ) = P ( A 1 ) ⋅ P ( B ∣ A 1 ) + P ( A 2 ) ⋅ P ( B ∣ A 2 ) P(B) = P(A1) \cdot P(B|A1) + P(A2) \cdot P(B|A2) P(B)=P(A1)⋅P(B∣A1)+P(A2)⋅P(B∣A2)
P ( B ) = 0.02 ⋅ 0.5 + 0.98 ⋅ 0.04 P(B) = 0.02 \cdot 0.5 + 0.98 \cdot 0.04 P(B)=0.02⋅0.5+0.98⋅0.04
P ( B ) = 0.01 + 0.0392 P(B) = 0.01 + 0.0392 P(B)=0.01+0.0392
P ( B ) = 0.0492 P(B) = 0.0492 P(B)=0.0492现在我们可以计算 $ P(A1|B) $:
P ( A 1 ∣ B ) = P ( B ∣ A 1 ) ⋅ P ( A 1 ) P ( B ) P(A1|B) = \frac{P(B|A1) \cdot P(A1)}{P(B)} P(A1∣B)=P(B)P(B∣A1)⋅P(A1)
P ( A 1 ∣ B ) = 0.5 ⋅ 0.02 0.0492 P(A1|B) = \frac{0.5 \cdot 0.02}{0.0492} P(A1∣B)=0.04920.5⋅0.02
P ( A 1 ∣ B ) = 0.01 0.0492 P(A1|B) = \frac{0.01}{0.0492} P(A1∣B)=0.04920.01
P ( A 1 ∣ B ) ≈ 0.2032 P(A1|B) \approx 0.2032 P(A1∣B)≈0.2032所以,长发的人是女生的概率大约是 20.32%。这个概率小于一般的女男比例(例如在某些高校可能是 25%),因此不建议前去搭讪。此外,考虑到在男生体检室门口等待的女生可能有男朋友的可能性,实际搭讪成功的概率可能会更低。因此,最好是利用这段时间学习概率论。
背景:根据临近期末统计每节课的到课率,分析期末月学生出勤概率
思考三:
假设某天概率论课老师已经提前通知了要考勤,根据相同情形下(即22级物联网同学课表排课一致的前提下,不受其他因素影响),一名物联网人决定旷课的概率是多少(课业压力相同的情况下)。
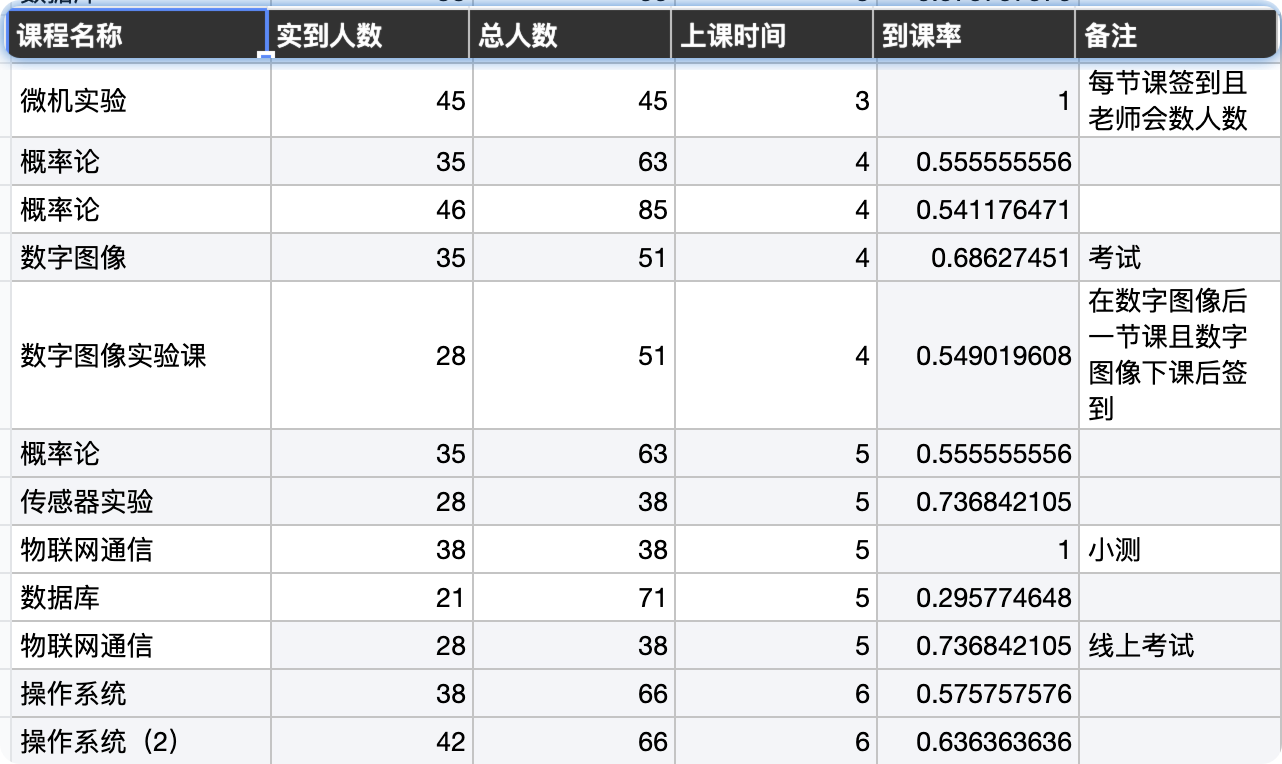
解答:由于深圳技术大学物联网学生的特殊性——根据近三周的数据统计,我们假设平均一周有15节课,根据收集数据记,一名学生在不知道老师会不会点名的情况下随机旷掉一节课的概率是0.5,而知道老师会点名的情况下旷课的概率是0.3,由于临近期末,老师的点名概率也稳定在(以概率论为例,平均三周下来的签到率为2/4=0.5)。如果一个学生决定下星期旷掉一节概率论,但是他担心老师会点名,所以他想知道值不值得为了大作业冒旷课的风险。
为了解决这个问题,我们可以使用概率论的知识来计算学生旷课时老师点名的概率以及学生因此可能面临的后果。
首先,我们知道学生随机旷掉一节课的概率是 P(旷课) = 0.5 ,而老师点名的概率是 P(点名) = 0.5 。
学生想知道在决定旷课的情况下,老师实际点名的概率。这是一个条件概率问题,可以用贝叶斯定理来解决。我们想要计算的是在学生旷课的情况下,老师点名的概率 P(点名|旷课) 。
根据贝叶斯定理:
P ( 点名 ∣ 旷课 ) = P ( 旷课 ∣ 点名 ) ⋅ P ( 点名 ) P ( 旷课 ) P(\text{点名}|\text{旷课}) = \frac{P(\text{旷课}|\text{点名}) \cdot P(\text{点名})}{P(\text{旷课})} P(点名∣旷课)=P(旷课)P(旷课∣点名)⋅P(点名)
其中:
- P(旷课|点名) 是在老师点名的情况下学生旷课的概率,根据题目是 0.3。
- P(点名) 是老师点名的概率,根据题目是 0.5。
- P(旷课) 是学生旷课的概率,根据题目是 0.5。
将这些值代入上述公式中:
P ( 点名 ∣ 旷课 ) = 0.3 × 0.5 0.5 P(\text{点名}|\text{旷课}) = \frac{0.3 \times 0.5}{0.5} P(点名∣旷课)=0.50.3×0.5
P ( 点名 ∣ 旷课 ) = 0.3 P(\text{点名}|\text{旷课}) = 0.3 P(点名∣旷课)=0.3这意味着如果学生决定旷课,那么老师实际点名的概率是 30%。这个概率相对于不考虑任何信息时的点名概率(50%)有所下降,但仍然是一个相对较高的概率。
因此,如果学生的大作业非常重要,且对成绩影响较大,那么他可能需要考虑这个风险是否值得冒。如果他能够承受因旷课可能带来的后果(如扣分或其他惩罚),那么他可能会选择旷课。如果后果严重,他可能需要考虑其他选项,比如请求补交作业或与老师沟通。



![[火灾警报系统]yolov5_7.0-pyside6火焰烟雾识别源码](https://img-blog.csdnimg.cn/img_convert/246ade3c09797e47af69d416f0b27504.jpeg)