零知识证明基础：数字签名

数字签名(Digital Signature)，也称电子签名，是指附加在某一电子文档中的一组特定的符号或代码。它利用密码技术对该电子文档进行关信息提取并进行认证形成，用于标识签发者的身份以及签发者对电子文档的认可，并能被接收者用来验证该电子文档在传输过程中是否被篡改或伪造。

数字签名是非对称密钥加密技术与数字摘要技术的应用。

数字签名技术一般分为带仲裁和不带仲裁的两类。如果使用对称密钥进行数字签名，则必须使用仲裁者，非对称可以不带仲裁。

为了满足身份认证、数据完整性和不可否认性等需求，数字签名具有以下特点：

数字签名流程简要介绍如下：

发送方用一个哈希函数 $H a s h ()$ 将要发送的消息生摘要（一串数字），然后用发送方的私钥对这个摘要进行加密，这个加密后的摘要将作为消息的数字签名和消息一起发送给接收方；
接收方首先用与发送方一样的哈希函数从接收到的原始消息中计算出消息摘要，接着用公钥对消息附加的数字签名进行解密，如果这两个摘要相同、那么接收方就能确认该消息是发送方的。

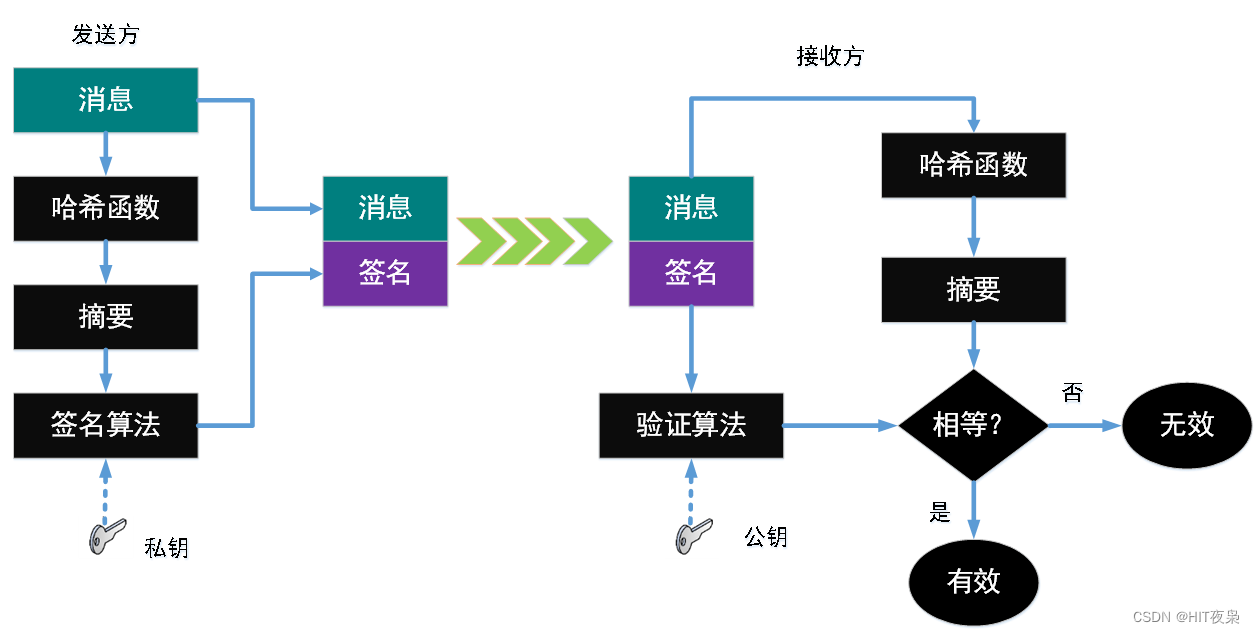
使用数字签名的好处在于：

一次数字签名涉及到一个哈希函数 $H a s h ()$ 、接收方的公钥、发送方的私钥。

RSA的签名方案流程如下：

1）生成公私密钥对
①选取两个大素数 $p$ 、 $p$ ，计算 $n = pq$ 及 $n$ 的欧拉函数 $\varphi(n) = (p-1)(q-1)$ ;
②随机选取整数 $e(1<e<\varphi(n))$ 作为公钥，满足 $\gcd(e,\varphi(n))=1$ ，即 $e$ 与 $\varphi(n)$ 互素;
③使用Euclid扩展算法计算私钥： $\equiv e^{-1} \mod \varphi(n)$ ，即 $e$ 的逆元(先选择 $e$ 再确定 $d$ 的原因是：加密的重要性大于解密的重要性)。
2）签名过程
设待签名的消息为 $m$ ，签名者利用安全的 $H a s h$ 函数产生消息摘要 $h = H a s h (m)$ ，然后计算签名： $\equiv h^d\mod n$ 。
3）验证过程
签名接收者收到消息 $m$ 和签名 $s$ ，计算消息摘要 $h = H a s h (m)$ ，然后，检验等式 $\mod n \equiv s^e \mod n$ 。若成立，则签名有效；否则签名无效。

签名时使用 $H a s h$ 函数可以防止利用同态的伪造攻击，有很好的抗攻击性。
RSA签名方案存在签名可重用的问题，同一消息在不同时刻签名不应是相同的。

RSA签名方案还存在签名可重用的问题，同一消息在不同时刻签名不应是相同的。这个问题可以通过在签名中引人随机数来解决。

基于椭圆曲线（Elliptic Curve）的签名是基于椭圆曲线的非对称密码体制在数字签名中的一个实现方案，即在椭圆曲线有限域上实现签名算法，其安全性依赖于椭圆曲线的有限域上的离散对数难题。

与RSA数字签名相比，在相同的安全强度条件下，基于椭圆曲线的签名方案签名长度短、存储空间小、计算速度快，特别适用于计算能力和存储空间有限、带宽受限、要求高速实现的场合。

基于椭圆曲线的签名方案流程如下：

1）生成公私密钥对
选择椭圆曲线 $E$ 一点 $G\in E$ ， $G$ 的阶为满足安全要求的素数 $n$ ，即 $n G = O$ 。
选取一个随机数 $d \in [1, n - 1]$ ，计算 $P_B$ 使得 $P_B=dG$ ，那么公钥为 $E,n,G,P_B)$ ，私钥为 $d$ 。
2）签名过程
用户随机选取整数 $k \in [1, n - 1]$ ，计算 $k G = (x, y)$ , $r≡x\mod n$ ；
待签名的消息为 $m$ ，计算 $e ＝ H a s h (m)$ ；
计算 $s≡(e+rd)k^{-1} \mod n$ ，如果 $r = 0$ 或 $s = 0$ ，则另选随机数 $k$ ，重新执行上面的过程，消息 $m$ 的签名为 $(r, s)$ 。
3）验证过程
签名接收者收到消息 $m$ 和签名 $(r, s)$ ;
计算 $e = H a s h (m)$ ；
计算 $u≡s^{-1}e\mod n$ , $v≡s^{-1}r\mod n$ ， $x_1,y_1)=uG+vQ,r_1≡x_1\mod n$ ；
判断 $r$ 和 $r_1$ 的关系，相等则签名有效，否则无效。