题意：为什么即使返回了相同的文本块，曼哈顿距离（Manhattan Distance）和余弦距离（Cosine Distance）之间还是存在差异？

问题背景：

I am using the qdrant DB and client for embedding a document as part of a PoC that I am working on in building a RAG.

I see that when I use a Manhattan distance to build the vector collection I get a high score than when I use the Cosine distance. However, the text chunk returned is the same. I am not able to understand why and how? I am learning my ropes here at RAG still. Thanks in advance.

我注意到，当我使用曼哈顿距离来构建向量集合时，得到的分数比使用余弦距离时要高。然而，返回的文本块是相同的。我无法理解为什么会这样以及是如何发生的。我还在RAG这里学习相关知识。提前感谢。

USER QUERY        使用查询

What is DoS?

COSINE DISTANCE        余弦距离

response: [
ScoredPoint(id=0, 
version=10, 
score=0.17464592, 
payload={
'chunk': "It also includes overhead bytes for operations, 
administration, and maintenance (OAM) purposes.\nOptical Network Unit 
(ONU)\nONU is a device used in Passive Optical Networks (PONs). It converts 
optical signals transmitted via fiber optic cables into electrical signals that 
can be used by end-user devices, such as computers and telephones. The ONU is 
located at the end user's premises and serves as the interface between the optical 
network and the user's local network."
}, 
vector=None, shard_key=None)
]

MANHATTAN DISTANCE                曼哈顿距离

response: [
ScoredPoint(id=0, 
version=10, 
score=103.86209, 
payload={
'chunk': "It also includes overhead bytes for operations, administration, 
and maintenance (OAM) purposes.\nOptical Network Unit 
(ONU)\nONU is a device used in Passive Optical Networks (PONs). It converts 
optical signals transmitted via fiber optic cables into electrical signals that 
can be used by end-user devices, such as computers and telephones. The ONU is 
located at the end user's premises and serves as the interface between the optical 
network and the user's local network."
}, 
vector=None, shard_key=None)
]

问题解决：

There are many different math functions that can be used to calculate similarity between two embedding vectors:

• Cosine distance,                                余弦距离
• Manhattan distance (L1 norm),         曼哈顿距离（Manhattan Distance，也称为L1范数）
• Euclidean distance (L2 norm),          欧氏距离（Euclidean Distance，也称为L2范数）
• Dot product,                                       点积（Dot Product）
• etc.

Each calculates similarity in a different way, where:

每种方法都以不同的方式计算相似度，其中：

余弦距离测量两个非零向量之间夹角的余弦值。余弦距离对向量的方向敏感，而对向量的大小（模长）不那么敏感。

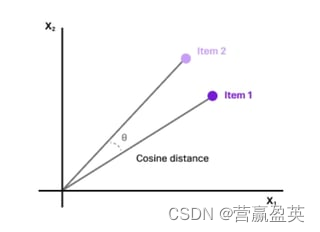
• The Cosine distance measures the cosine of the angle between two non-zero vectors. The Cosine distance is sensitive to the direction of the vectors and is less sensitive to the magnitude.
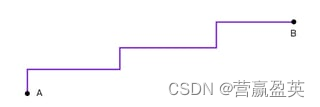
• The Manhattan distance measures the absolute difference between the corresponding elements of two vectors. The Manhattan distance is sensitive to the magnitude of the vectors.

曼哈顿距离测量两个向量对应元素之间的绝对差值。曼哈顿距离对向量的大小（模长）敏感。

• The Euclidean distance measures the straight-line distance between two vectors.

欧氏距离测量两个向量之间的直线距离。

• The Dot product measures the angle between two vectors multiplied by the product of their magnitudes.

点积测量两个向量之间的角度，并乘以这两个向量模长的乘积。

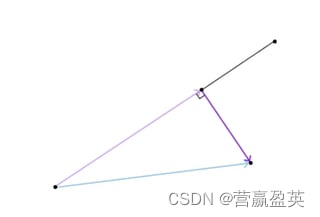
Consequently, the results of similarity calculations are different, where:

因此，相似度计算的结果是不同的，其中：

• The Cosine distance is always in the range [0, 2]. 

余弦距离（实际上是1减去余弦相似度得到的值）总是在[0, 2]的范围内。

• The Manhattan distance is always in the range [0, ∞).

曼哈顿距离总是在[0, ∞)的范围内。

• The Euclidean distance is always in the range [0, ∞).

欧氏距离总是在[0, ∞)的范围内。

• The Dot product is always in the range (-∞, ∞).

See the table below.

Measure 试题	Range 范围	Interpretation  解释
Cosine distance 余弦距离	[0, 2]	0 if vectors are the same, 2 if they are diametrically opposite. 如果向量相同则为0，如果它们完全相反则为2。
Manhattan distance 曼哈顿距离	[0, ∞)	0 if vectors are the same, increases with the sum of absolute differences. 如果向量相同则为0，随着绝对差值的和的增加而增加。
Euclidean distance 欧氏距离	[0, ∞)	0 if vectors are the same, increases with the sum of squared differences. 如果向量相同则为0，随着平方差的和的增加而增加。
Dot product 点积	(-∞, ∞)	Measures alignment, can be positive, negative, or zero based on vector direction. 测量对齐性，可以根据向量的方向为正、负或零。