数据结构-顺序表的插入排序

顺序表的排序可以看作数组排序的拓展。基本逻辑和数组排序的逻辑大同小异。

由于顺序表中可以存放不同种的数据类型，进而和结构体排序又有相似之处。其中要注意的是（->）和（.）的区别。

-> 符号是针对指针进行的操作，而 . 则是针对结构体的数据进行操作。

顺序表的初始化

const int M = 505;typedef struct{int key;            //关键元素int others;         //其他元素
}info;typedef struct{info r[M+1];        int length();       //表长
}SeqList,*PSeqList;

直接插入排序

分析：

直接插入排序是最简单的排序。本质是将顺序表中的数据依次插入新的序列并使之有序的过程。

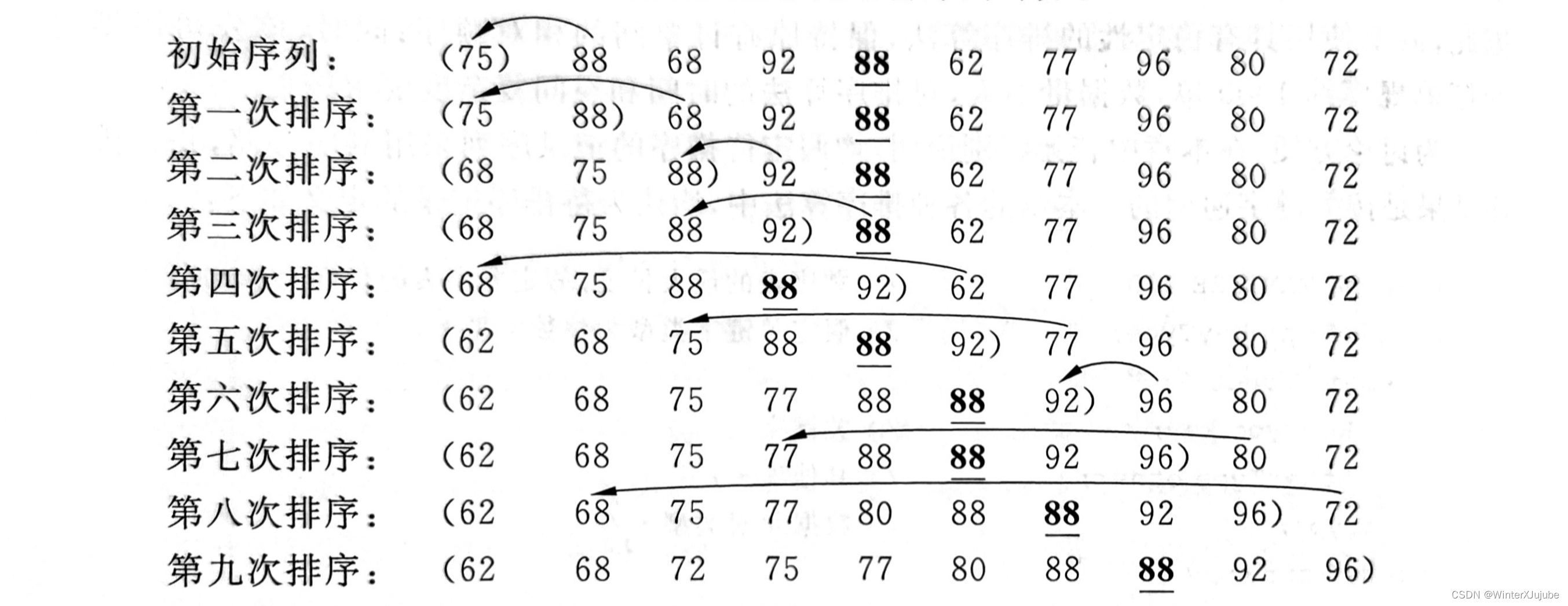
在这个过程中，数字88的和88的相对位置没有发生改变，所以这个排序是稳定的。

void Insert_Sort(PSeqList PL)
{int p;for(int i = 2;i <= PL->length;i++){p = PL->r[i];            //标记int j = i-1;while(PL->r[0].key < PL->r[j].key;{PL->r[j+1] = PL->r[j];j--;}PL->r[j+1] = p;         //插入}
}

复杂度：

空间复杂度

在空间上只使用了一个变量 p 进行转存操作。所以空间复杂度是 $O(1)$ 。

时间复杂度

最好的情况是所有的数据已经有序，每次操作只需要把顺序表中的数据依次放入新序列即可。总的比较次数为 $n-1$ 次，总的移动次数为 $2(n-1)$ 次。因此时间复杂度是 $O(n)$ 。

最坏的情况是所有的数据逆序排列，每次操作都需要把这次操作的数据与新序列中每一个数据进行比较。第 $i$ 趟的比较次数为 $i+1$ ，移动次数为 $i+2$ 。

总的比较次数 $\sum_{i = 2}^{n}i\approx \frac{n^{2}}{2}$ ，总的移动次数 $\sum_{i = 2}^{n}(i+2)\approx \frac{n^{2}}{2}$ 。因此时间复杂度是 $O(n^{2})$

一般情况下当处理第 $i$ 个元素 $s_{i}$ 时，有 $i$ 个可能的插入位置。假设每个位置的可能性相同。均为 $1/i$ ，比较次数为 $j$ ，则平均的比较次数为 $\sum_{j=1}^{i}\frac{1}{i}\times j=\frac{i+1}{2}$ 。而直接插入排序的总比较次数为 $\sum_{n}^{i=2}(\frac{i+1}{2})=\frac{n-1}{2}+\frac{(n-1)\times (n+2)}{2}\approx \frac{n^{2}}{4}$ 。一般情况下平均比较次数和平均移动次数为同一数量级，所以直接插入排序的时间复杂度为 $O(n^{2})$

二分插入排序

分析：

使用二分查找的思路和插入排序相结合，可以大幅度减少时间复杂度，并且是稳定的排序。

二分查找：

设顺序表中的结点按关键字递增，首先将待查值 $k$ 和表中间位置上的结点关键字 $mid$ 进行比较。若二者相等，则查找成功。否则，如果 $k<mid$ ，则在表的前半部分继续利用二分查找，反之，则在表的后半部分二分查找，如此进行下去直至查找结束。

二分查找的时间复杂度为 $O(\log_{2} n)$ 。

二分插入排序代码：

void BinInsert_Sort(PSeqList PL)
{int l,h,mid;int p;for(int i = 2;i <= PL->length;i++){p = PL->r[i];                    //标记l = 1;                           //设置区间h = i-1;while(l <= h)                    //循环查找{mid = (l+h) >> 1;if(PL->r[0].key >= PL->r[mid].key)l = mid+1;               //查找右半部分else    h = mid - 1;         //查找左半部分}for(int j = i-1;j >= h+1;j--)    //顺序表插入操作PL->r[j+1] = PL->r[j];        PL->r[h+1] = p;                  //插入}
}

复杂度：

空间复杂度

与直接插入排序相同为 $O(1)$ 。

时间复杂度

与直接插入排序相比，二分插入排序的比较次数与待排序的初始状态无关，只与记录的个数有关。

插入第 $i$ 个记录时，比较次数最多为 $\left \lfloor log_{2}i \right \rfloor +1=\left \lceil log_{2}i \right \rceil$ 。所以 $n$ 个记录排序的总比较次数为 $\sum_{i=1}^{n}\left \lceil log_{2}i \right \rceil \approx n \times log_{2}n$ 。