trie[讲课留档]

字典树

1.字典树简介

字典树 ( Trie 树 ) 又称单词查找树，
是一种用于在字符串集合中高效地存储和查找字符串的树形数据结构。

我们首先通过一张图来理解字典树的结构：

在这里插入图片描述

我们假定结点的顺序按照图中给定的顺序进行编号，容易发现，在一棵给定的树上，每一条树边代表一个字母。那么我们可以知道：从根节点出发，到达某个指定的结点的路径可以构成一个字符串。

一个例子： 1 → 4 → 8 → 13 ⟹ c a a 1\to4\to 8\to 13 \Longrightarrow caa 1→4→8→13⟹caa

在这里插入图片描述

2.应用场景

维护一个 字符串集合 ，支持两种操作：

向集合中插入一个字符串 xx；
询问一个字符串 xx 及其作为前缀在集合中出现了多少次。
例如：有字符串集合 { “abc” , “acwing” , “hhhh”}

  1. 插入字符串 “abc” ==> 集合 { “abc” , “abc” , “acwing” , “hhhh”}
  2. 查询字符串 “abc” 出现的次数：2 次。

Trie 的结构非常好懂，我们用 δ ( u , c ) \delta(u,c) δ(u,c)表示结点 u u u 的 c c c 字符指向的下一个结点，或着说是结点 u u u 代表的字符串后面添加一个字符 c c c 形成的字符串的结点。

有时需要标记插入进 Trie 的是哪些字符串，每次插入完成时在这个字符串所代表的节点处打上标记即可。

3.具体操作
(1) 插入

基本思路：将字符串逐个拆分成单个字符，从第一个字符开始与Trie 树的根结点开始的子结点比对，若有结点具有相同的字符，则以同样的方式对比下一个字符与该结点的子结点 。

那么插入操作就应该分为以下的步骤：

  1. 首先我们需要记录根结点的编号，初始化为0；
  2. 从左到右扫描这个单词，每次计算关系编号 i d id id ；
  3. 如果之前没有从 r o o t root root 到 i d id id 的前缀，则插入该编号(需要预先在声明计数变量，对一种编号进行记录)；
  4. 执行 r o o t = t r e e [ r o o t ] [ i d ] r o o t = t r e e [ r o o t ] [ i d ] root=tree[root][id] ，表示顺着字典树继续向下走。

注意：在插入完字符串之后，要给（末尾的）结点加上结束标记。

在这里插入图片描述

(2) 查找

与插入操作的原理基本相同，将需要查询的字符串逐个拆分成单个字符，逐个与 Trie 树中的结点比较，直至发现 Trie 树中不存在的字符，或要查询的字符串的各个字符都比较完成 。

  • 对于发现 Trie 树中不存在的字符，一旦发现，就能确定要查询的字符串不属于原集合。

  • 对于要查询的字符串的各个字符都比较完成，则存在两种情况：

    ① 要查询的字符的确属于集合；

    ② 要查询的字符是集合中某个字符串的前缀。

    此时就需要用到刚刚打上的结束标记来判断了。

4.代码实现

P8306 【模板】字典树 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

初始化：
int son[N][70]; // 存储每个结点的所有儿子结点
int cnt[N]; // 记录以这个结点结尾的单词有多少个, 作为字符串结束标记
int idx; // 存储当前已经使用到的结点的下标 
// 下标是 0 的结点，既是根节点，又是空结点
map<char,int>mp;//处理字符
char str[N]; // 存储输入的字符串void init_char() {for (char i = 'a'; i <= 'z'; ++i) mp[i] = ++idx;for (char i = 'A'; i <= 'Z'; ++i) mp[i] = ++idx;for (char i = '0'; i <= '9'; ++i) mp[i] = ++idx;
}void init_son() {for (int i = 0; i <= tot; ++i) {cnt[i] = 0;for (int j = 0; j <= 62; ++j) {son[i][j]=0;}}
}
插入
void insert(string t) {int p = 0;for (auto x: t) {if (!son[p][mp[x]]) son[p][mp[x]] = ++idx;p = son[p][mp[x]];cnt[p] ++;}
}
查找
int query(string t) {int p = 0;for (auto x: t) {if (!son[p][mp[x]]) return 0;p = son[p][mp[x]];}return cnt[p];
}

AC代码:

#include <bits/stdc++.h>
using namespace std;
#define io ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
typedef long long ll;
//#define int ll
#define pb push_back
#define eb emplace_back
#define m_p make_pair
const int mod = 998244353;
#define mem(a,b) memset(a,b,sizeof a)
#define pii pair<int,int>
#define fi first
#define se second
const int inf = 0x3f3f3f3f;
const int N = 3e6 + 50;
//__builtin_ctzll(x);后导0的个数
//__builtin_popcount计算二进制中1的个数int son[N][70]; // 存储每个结点的所有儿子结点
int cnt[N]; // 记录以这个结点结尾的单词有多少个, 作为字符串结束标记
int idx; // 存储当前已经使用到的结点的下标 
// 下标是 0 的结点，既是根节点，又是空结点
map<char,int>mp;//处理字符
char str[N]; // 存储输入的字符串void init_char() {for (char i = 'a'; i <= 'z'; ++i) mp[i] = ++idx;for (char i = 'A'; i <= 'Z'; ++i) mp[i] = ++idx;for (char i = '0'; i <= '9'; ++i) mp[i] = ++idx;
}void init_son() {for (int i = 0; i <= idx; ++i) {cnt[i] = 0;for (int j = 0; j <= 62; ++j) {son[i][j] = 0;}}
}void insert(string t) {int p = 0;for (auto x: t) {if (!son[p][mp[x]]) son[p][mp[x]] = ++idx;p = son[p][mp[x]];cnt[p] ++;}
}int query(string t) {int p = 0;for (auto x: t) {if (!son[p][mp[x]]) return 0;p = son[p][mp[x]];}return cnt[p];
}void work() {int n, q; cin >> n >> q;init_son();idx = 0;for (int i = 1; i <= n; ++i) {string s; cin >> s;insert(s);}for (int i = 1; i <= q; ++i) {string t; cin >> t; cout << query(t) << '\n';} 
}signed main() {io;int t = 1;init_char();cin >> t;while (t--) {work();}return 0;
}

课后练习：P2580 于是他错误的点名开始了 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

5.算法分析

Trie的核心思想是空间换时间，利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。

假设字符的种数有m个，有若干个长度为n的字符串构成了一个Trie树，则每个节点的出度为m（即每个节点的可能子节点数量为m），Trie树的高度为n。很明显我们浪费了大量的空间来存储字符，此时Trie树的最坏空间复杂度为 O ( m n ) O(m^n) O(mn)。

也正由于每个节点的出度为m，所以我们能够沿着树的一个个分支高效的向下逐个字符的查询，而不是遍历所有的字符串来查询，此时Trie树的最坏时间复杂度为O(n)。这正是空间换时间的体现，也是利用公共前缀降低查询时间开销的体现。

6.拓展

01trie

简化版trie，树边不再是一个字符，而是0或1作为二进制的一个位，可以理解为：每一个数写成二进制都是一个字符串，我们存数的时候把这个01字符串存下去，由高位到低位 = 由树根到叶节点。

[U109895 HDU4825]Xor Sum - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

对于每一个数字都可以二进制拆位，从高位到低位加入字典树。分析数组大小，最多有N个数，每个数最多不超过 2 32 2^{32} 232，拆位出来每个数最多是一个长度为32的链，最多有N*32个节点，每一个节点的子节点最多有2种状态即01。

查找异或时，贪心地去找，从高位到低位，如果该位上有异或为1的数选择该类一定是更优的，依次找到即可。

AC代码:

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 5e5;
int tree[N*32+10][3];
int cnt[N];
int idx;void insert_tr(int t){int p = 0;for(int bit = 32; bit >= 0;bit--){int u = (t >> bit) & 1ll;if(!tree[p][u]) tree[p][u] = ++idx;p = tree[p][u];}
}int querry_tr(int t){int ans = 0;int p = 0;for(int bit = 32; bit >= 0;bit--){int u = (t >> bit) & 1ll;if(tree[p][!u]){ans += (1ll << bit) * (!u);p = tree[p][!u];} else{ans += (1ll << bit) * (u);p = tree[p][u];} }return ans;
}
signed main(){ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);int n,m;cin >> n >> m;int t;for(int i=0;i<n;i++){cin >> t;insert_tr(t);}for(int i=0;i<m;i++){cin >> t;cout << querry_tr(t) << '\n';}return 0;
}

可以尝试带删01trieProblem - 706D - Codeforces

第一周周赛团队赛Problem - 6955 (hdu.edu.cn)

*7.提提提提提高

P4735 最大异或和 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

每一次增加一个x，对所有后缀异或和都要修改一次，时间复杂度过大，考虑优化，把后缀和变成前缀和：
s [ 1 ] = a [ 1 ] s [ 2 ] = a [ 1 ] ⊕ a [ 2 ] s [ 3 ] = a [ 1 ] ⊕ a [ 2 ] ⊕ a [ 3 ] ⋯ s [ p − 1 ] ⊕ s [ n ] = a [ p ] ⊕ a [ p + 1 ] ⊕ ⋯ ⊕ a [ n ] \begin{align} s[1]& = a[1]\\ s[2]& = a[1] \oplus a[2]\\ s[3]& = a[1] \oplus a[2] \oplus a[3]\\ &\cdots \\ s[p - 1] \oplus s[n] & = a[p]\oplus a[p + 1] \oplus \cdots \oplus a[n] \end{align} s[1]s[2]s[3]s[p−1]⊕s[n]​=a[1]=a[1]⊕a[2]=a[1]⊕a[2]⊕a[3]⋯=a[p]⊕a[p+1]⊕⋯⊕a[n]​​
此时查询变成了，在[l - 1, r - 1]内找一个p，使得 s [ p ] ⊕ s [ n ] ⊕ x s[p] \oplus s[n] \oplus x s[p]⊕s[n]⊕x 最大，而 s [ n ] ⊕ x s[n] \oplus x s[n]⊕x已经是一个定值。

如果我们不设置p在[l - 1, r - 1]的范围，就是一个简单的01trie，但是我们现在需要记录每一个数的位置版本，就需要让这个树可持久化。

可持久化字典树！！！
可持久化：

是一个重要的算法思想，结合备份与函数式编程的思想。

部分可持久化 (Partially Persistent)：所有版本都可以访问，但是只有最新版本可以修改。

既然我们现在要记录所有历史版本，最直观的想法就是将每一个版本的 trie 都存储下来，当需要一个新的结点时，我们完全复制一个历史版本，然后再它上面完成操作。这样的做法，正确性是显然的，但是空间开销非常大。要减少存储空间，我们考虑将 trie 树上的一些“枝条”共用来减少空间上的浪费。

我们在每一个新的数字插入的时候创建一个新版本来做，而不是插入原来的版本，同时要记录新建的树的每个节点的版本号，然后完全复制历史版本上同等地位点的其他儿子信息。

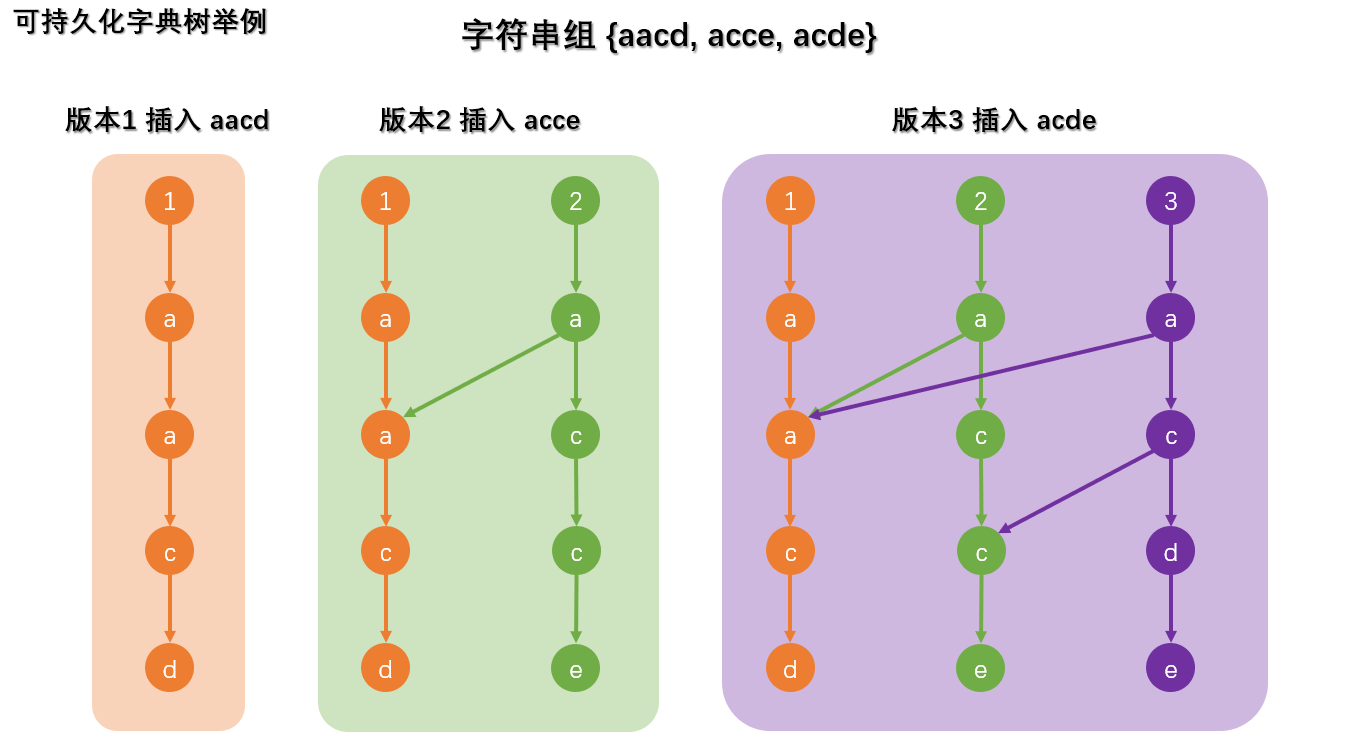
在这里插入图片描述

在上图中，从一个版本起点开始，遍历整棵树，一定能获得该版本及之前的所有串，并且空间大大减少。

大部分的可持久化 Trie 题中，Trie 都是以01-Trie的形式出现的，所以我们在这里只学习可持久化01trie的写法。

回到题目！

需要开的变量：
int son[N * 25][2];//trie
int root[N * 25];//根节点编号,root[x] 表示第x版本的根节点编号
int maxid[N * 25];//节点的版本号,maxid[x] 表示编号为x的节点的版本
int s[N], a[N];//前缀和，原数组
int idx = 0;//节点编号
插入：
void insert(int i, int k, int pre, int now) { //当前版本号，当前位数，上一个版本在当前状态的节点编号，当前版本在当前状态的节点编号if (k < 0) {maxid[now] = i; return;}int t = (s[i] >> k) & 1;if (pre) son[now][t ^ 1] = son[pre][t ^ 1];son[now][t] = ++idx;insert(i, k - 1, son[pre][t], son[now][t]);maxid[now] = i;
}
查找：

查找的时候为了保证p在[l - 1, r - 1]范围内，我们从第r - 1个版的根节点开始找，该版本包含了之前的所有数，而且不含后面版本的东西，贪心地去找，如果找到的节点版本大于等于l - 1就可以跳过去，否则就不能跳过去，一直找到叶子节点会得到最终的版本号x = maxid[p]，我们会发现从r - 1一路跳过来得到的01序列正是在r - 1版本中的x枝，代表了贪心选择后的最大值是属于第x个版本，答案就是s[x]^num。

ll query(int rt, int l, int num) {int p = rt;for (int i = 23; i >= 0; --i) {int t = (num >> i) & 1;if (son[p][t ^ 1] && maxid[son[p][t ^ 1]] >= l) p = son[p][t ^ 1];else p = son[p][t];}return num ^ s[maxid[p]];
}
注意点：

  1. 需要开一个第0版本。

    为什么？

    当l = 1时，我们有可能会选择到s[l - 1]即s[0]，所以第0版应该加入一个0。

  2. maxid[0] = -1.

    如果maxid[0] = 0则表示了编号为0的节点版本号是0，但事实上，0号节点代表空节点，没有任何有意义的节点编号为0，而版本号为0的树也有自己的节点，不能随便加一个无意义的空点。

AC代码:

#include <bits/stdc++.h>
using namespace std;
#define io ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
typedef long long ll;
#define int ll
#define pb push_back
#define eb emplace_back
#define m_p make_pair
const int mod = 998244353;
#define mem(a,b) memset(a,b,sizeof a)
#define pii pair<int,int>
#define fi first
#define se second
const int inf = 0x3f3f3f3f;
const int N = 6e5 + 50;
//__builtin_ctzll(x);后导0的个数
//__builtin_popcount计算二进制中1的个数
int son[N * 25][2];
int root[N * 25];//根节点编号,root[x] 表示第x版本的根节点编号
int maxid[N * 25];//节点的版本号,maxid[x] 表示编号为x的节点的版本
int s[N], a[N];//前缀和，原数组
int idx = 0;void insert(int i, int k, int pre, int now) {if (k < 0) {maxid[now] = i; return;}int t = (s[i] >> k) & 1;if (pre) son[now][t ^ 1] = son[pre][t ^ 1];son[now][t] = ++idx;insert(i, k - 1, son[pre][t], son[now][t]);maxid[now] = i;
}ll query(int rt, int l, int num) {int p = rt;for (int i = 23; i >= 0; --i) {int t = (num >> i) & 1;if (son[p][t ^ 1] && maxid[son[p][t ^ 1]] >= l) p = son[p][t ^ 1];else p = son[p][t];}return num ^ s[maxid[p]];
}void work() {int n, m; cin >> n >> m;root[0] = ++idx;maxid[0] = -1;insert(0, 23, 0, root[0]);for (int i = 1; i <= n; ++i) {cin >> a[i];s[i] = s[i - 1] ^ a[i];root[i] = ++idx;insert(i, 23, root[i - 1], root[i]);}while (m--) {char ch; cin >> ch; if (ch == 'A') {int x; cin >> x; n++;s[n] = s[n - 1] ^ x;root[n] = ++idx;insert(n, 23, root[n - 1], root[n]);} else {int l, r, x; cin >> l >> r >> x;cout << query(root[r - 1], l - 1, x ^ s[n]) << '\n';}}
}signed main() {io;int t = 1;// cin >> t;while (t--) {work();}return 0;
}

谢谢大家！

参考及引用：
Trie 字典树 详解
trie 树及其可持久化

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/365570.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

Golang-slice理解

Golang-slice理解

slice golang-slice语雀笔记整理 slicego为何设计slice&#xff1f;引用传递实现扩容机制 go为何设计slice&#xff1f; 切片对标其他语言的动态数组&#xff0c;底层通过数组实现&#xff0c;可以说是对数组的抽象&#xff0c;底层的内存是连续分配的所以效率高&#xff0c;可…
阅读更多...
Spring Boot项目的两种发布方式

Spring Boot项目的两种发布方式

一、通过jar包发布 1、在pom中添加一个SpringBoot的构建的插件 <build><plugins><plugin><groupId>org.springframework.boot</groupId><!--自动检测项目中的 main 函数--><artifactId>spring-boot-maven-plugin</artifactId>…
阅读更多...
一文get懂kwai短视频助力巴西博弈slots游戏广告优势

一文get懂kwai短视频助力巴西博弈slots游戏广告优势

一文get懂kwai短视频助力巴西博弈slots游戏广告优势 在数字化时代&#xff0c;短视频广告凭借其独特的魅力和高效的传播方式&#xff0c;成为了各大品牌进行营销推广的重要手段。特别是在巴西这个充满活力的国家&#xff0c;kwai短视频广告以其独特的方式&#xff0c;为博弈游…
阅读更多...
2024企业数据资产化及数据资产入表方案梳理

2024企业数据资产化及数据资产入表方案梳理

01 数据资产入表&#xff1a;是一个将组织的各类数据资产进行登记、分类、评估和管理的流程。 数据资产包括&#xff1a;客户信息、交易记录、产品数据、财务数据等。 做个比喻吧&#xff1a;数据资产入表就像是给公司的数据资产做“人口普查”—— ①找出公司有哪些数据找…
阅读更多...
Pytorch课程论文设计参考

Pytorch课程论文设计参考

Pytorch下基于卷积神经网络的手写数字识别 论文格式 利用wps初步美化论文格式教程 wps论文格式变的的原因 格式变的根本原因是word为流式文件&#xff0c;就算同是word同一个版本不同电脑也会有可能变&#xff0c;字体变是因为没有嵌入字体然后观看的那台没有这个字体。 一、…
阅读更多...
机器学习环境搭建

机器学习环境搭建

前言 个人笔记&#xff0c;记录框架和小问题&#xff0c;没有太详细记载。。 1、Anaconda安装 下载地址&#xff1a; Free Download | Anaconda &#xff08;慢&#xff09; ​ 国内镜像&#xff1a;https://link.csdn.net/?targethttp%3A%2F%2Fitcxy.xyz%2F241.html 下载…
阅读更多...
【硬件开发】安规电容X电容和Y电容

【硬件开发】安规电容X电容和Y电容

为什么有安规电容 国家为了保护人民的安全要求&#xff0c;电容器失效后&#xff0c;不会导致电击&#xff0c;不危及人身安全的安全电容器 安规电容的作用 滤除雷电冲击波&#xff0c;以及插拔插座的高频噪声 X电容 聚酯电容 位置 X电容位于火线和零线之间 作用 滤除…
阅读更多...
Bunny的PT+SFT训练

Bunny的PT+SFT训练

GitHub - BAAI-DCAI/Bunny: A family of lightweight multimodal models.A family of lightweight multimodal models. . Contribute to BAAI-DCAI/Bunny development by creating an account on GitHub.https://github.com/BAAI-DCAI/Bunny1.环境安装 conda create -n bunny …
阅读更多...
观测云产品更新 | Pipelines、智能监控、日志数据访问等

观测云产品更新 | Pipelines、智能监控、日志数据访问等

观测云更新 Pipelines 1、Pipelines&#xff1a;支持选择中心 Pipeline 执行脚本。 2、付费计划与账单&#xff1a;新增中心 Pipeline 计费项&#xff0c;统计所有命中中心 Pipeline 处理的原始日志的数据大小。 监控 1、通知对象管理&#xff1a;新增权限控制。配置操作权…
阅读更多...
经典小游戏（一）C实现——三子棋

经典小游戏（一）C实现——三子棋

switch(input){case 1:printf("三子棋\n");//这里先测试是否会执行成功break;case 0:printf("退出游戏\n");break;default :printf("选择错误&#xff0c;请重新选择!\n");break;}}while(input);//直到输入的结果为假&#xff0c;循环才会结束} …
阅读更多...
springboot是否可以代替spring

springboot是否可以代替spring

Spring Boot不能直接代替Spring&#xff0c;但它是Spring框架的一个扩展和增强&#xff0c;提供了更加便捷和高效的开发体验。以下是关于Spring Boot和Spring关系的详细解释&#xff1a; Spring框架&#xff1a; Spring是一个广泛应用的开源Java框架&#xff0c;提供了一系列模…
阅读更多...
什么是有效的电子签名？PDF电子签名怎样具备法律效力？

什么是有效的电子签名？PDF电子签名怎样具备法律效力？

电子签名逐渐成为商务文书和法律文件中不可或缺的一部分。《电子签名法》自2005年4月1日起施行&#xff0c;这一立法是中国信息化法律的重要里程碑&#xff0c;为电子签名应用奠定了法律基础。电子签名不仅仅是一种技术手段&#xff0c;更是一种法律认可的签名形式。那么究竟什…
阅读更多...
跨模型知识融合：大模型的知识融合

跨模型知识融合：大模型的知识融合

大模型&#xff08;LLMs&#xff09;在多个领域的应用日益广泛&#xff0c;但确保它们的行为与人类价值观和意图一致却充满挑战。传统对齐方法&#xff0c;例如基于人类反馈的强化学习&#xff08;RLHF&#xff09;&#xff0c;虽取得一定进展&#xff0c;仍面临诸多难题&#…
阅读更多...
百刀神书！从0搭建神经网络！我服！

百刀神书！从0搭建神经网络！我服！

《Neural Networks from Scratch in Python》是一本深入浅出的书籍&#xff0c;旨在帮助读者从零开始理解和实现神经网络模型。作者使用Python语言&#xff0c;从基本的数学概念和神经网络的基本原理开始&#xff0c;逐步引导读者探索神经网络的各个组成部分。 该书介绍了神经…
阅读更多...
AI数字人直播系统源码解析:教你如何高效搭建直播系统！

AI数字人直播系统源码解析:教你如何高效搭建直播系统！

在人工智能技术飞速发展的今天&#xff0c;以AI数字人直播为代表的数字人应用开始为各大企业引进&#xff0c;并引发了一场“AI数字人直播浪潮”。在此背景下&#xff0c;许多创业者都感受到了所蕴含着的巨大前景和收益空间&#xff0c;从而有了搭建AI数字人直播系统的想法&…
阅读更多...
BGE M3-Embedding 模型介绍

BGE M3-Embedding 模型介绍

BGE M3-Embedding来自BAAI和中国科学技术大学&#xff0c;是BAAI开源的模型。相关论文在https://arxiv.org/abs/2402.03216&#xff0c;论文提出了一种新的embedding模型&#xff0c;称为M3-Embedding&#xff0c;它在多语言性&#xff08;Multi-Linguality&#xff09;、多功能…
阅读更多...
Ollama中文版部署

Ollama中文版部署

M1部署Ollama Ollama中文网站: Featured - 精选 - Ollama中文网 下载网址: Download Ollama on macOS 安装后运行llma3模型: ollama run llama3:8b 界面使用: GitHub - open-webui/open-webui: User-friendly WebUI for LLMs (Formerly Ollama WebUI) 部署open-webui: do…
阅读更多...
FT232串口win11打不开，重新安装驱动问题解决。

FT232串口win11打不开，重新安装驱动问题解决。

问题现象&#xff1a;FT232 WIN11打不开&#xff0c;串口识别正在被占用。更改串口号问题无法解决。 解决办法&#xff1a; 卸载驱动&#xff0c; 重启电脑&#xff0c; 去官网下驱动安装问题解决。Drivers - FTDI
阅读更多...
原神最大数据泄露事件！

原神最大数据泄露事件！

你知道吗&#xff1f; 一位黑客公开了原神的内部资料&#xff0c;并对米哈油的网络安全表示失望。那么他为什么要这样做呢&#xff1f; 前段时间&#xff0c;由于单方面对原神游戏设计的不满&#xff0c;黑客对米哈游进行了入侵。未被公开的新角色、新地图&#xff0c;甚至是…
阅读更多...
简易深度学习（1）深入分析神经元及多层感知机

简易深度学习（1）深入分析神经元及多层感知机

一、神经元 单个神经元结构其实可以认为是一个线性回归模型。例如下图中 该神经元输入为三个特征&#xff08;x1&#xff0c;x2&#xff0c;x3&#xff09;&#xff0c;为了方便理解&#xff0c;大家可以认为每条线上都有一个权重和特征对应&#xff08;w1&#xff0c;w2&…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023