引自代码随想录
一、[77]组合
给定两个整数 n 和 k,返回 1 ... n 中所有可能的 k 个数的组合。
示例: 输入: n = 4, k = 2 输出: [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4]]
1、大致逻辑
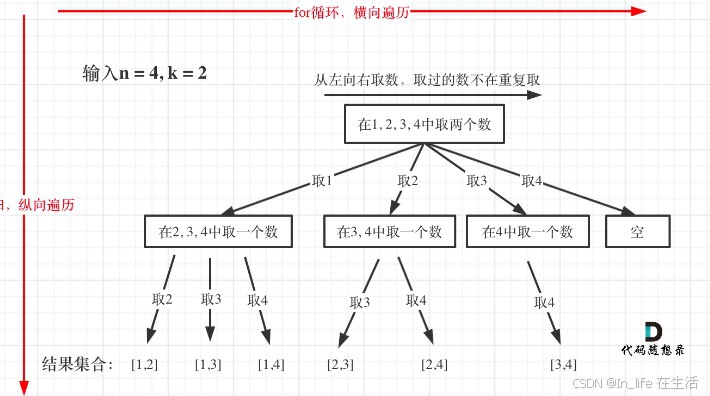
k为树的深度,到叶子节点的路径即为一个结果
开始索引保证不重复取数(从当前位置往后取值)
每一个节点为一个for循环
2、剪枝(优化)
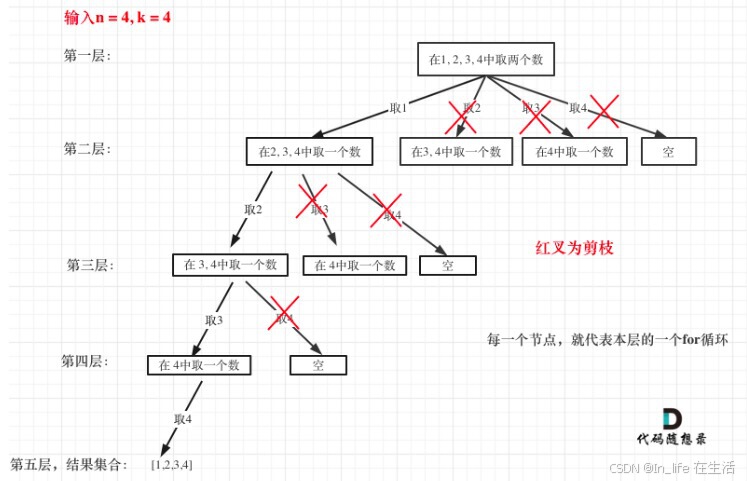
(1)和大于n,结束递归。
(2)剩余元素不足以满足k(k个元素)
剩下所需元素:k-path.size()
至多从该起始位置开始遍历(否则元素个数不够):n - (k - path.size()) + 1
为什么有个+1呢,因为包括起始位置(从起始位置开始遍历)
我们要是一个左闭的集合(重要!!!!)
path.size() : 已经找的个数
k-path.size() :还需找的个数
[x, n]的数组长度起码应该是k-path.size()才有继续搜索的可能
那么 n-x+1 = k-path.size()
解方程得 x = n+1 - (k-path.size()),
而且这个x是可以作为起点往下搜的
也就是for(i = s; i<=x; i++) 这里的x是可以取到的
类似题目[216]、[17](有点难度)、[39]、[40](需要对开始索引做处理)






![[每周一更]-(第103期):GIT初始化子模块](https://img-blog.csdnimg.cn/direct/9c71a0fe979140c29433620914d491af.jpeg#pic_center)