---

期刊: IEEE Trans. Vis. Comput. Graph.（发表日期: 2019）
作者: Johanna Schmidt; Dominik Fleischmann; Bernhard Preim; Norbert Brändle; Gabriel Mistelbauer

摘要

时间数据可视化用于分析随时间变化的因变量，其中时间是一个独立变量。由于需要向用户传达许多方面的信息（例如，时间和变量的变化），可视化时间数据本质上是困难的。这是可视化中的一个重要主题，已经设计了许多处理不同任务的可视化技术。在本文中，我们提出了一种新颖的概念——弹出图（popup-plots），其中利用常见的3D旋转交互来浏览数据。这使用户能够从不同的角度查看数据，而无需学习和适应新的交互概念。因此，弹出图是一种新颖的可视化和与时间相关的因变量交互方法。我们通过根据时间弯曲空间来扩展2D图来加入时间信息。弯曲是基于球坐标系方法计算的，其受到朝向图的视角的持续影响。因此，可以从不同的角度观察图，之间无缝切换，提供了分析所表示数据不同方面的可能性。由于当前视角是通过数据的形状来表示的，用户可以推断出当前查看的数据的哪一部分。时间信息被编码到可视化本身中，类似于树的年轮。我们通过将其应用于来自两个不同领域的数据（包括随时间的空间位置上的测量），以及评估我们解决方案的可用性来演示我们的方法。

关键词：时态数据、时间相关可视化、3D 绘图、椭球坐标系。

1 引言

时空数据集的可视化本质上是一项具有挑战性的任务[1]，因为必须以视觉方式传达时间背景、随时间的变化以及因变量之间的关系。因此，时间相关数据可视化 [2] 是一个新兴主题，应用于许多不同领域。

在许多情况下，时间数据集由在连续时间点获取的测量值组成。此类测量值可以是温度 [3]、交通量 [4]、医疗参数 [5] 或可能随时间变化的其他测量值。我们将此类测量称为属性。为了保持一致性，并且为了能够比较随时间变化的值，测量结果经常记录在固定的空间位置。我们将这些位置称为地标。作为此类数据集的一个示例，我们可以想象一份温度值记录，该记录是在一个月内每天使用固定温度计在特定空间位置测量的。地标、属性和时间的组合类似于 3D 数据集，包含两个因变量（属性和地标）和自变量时间。不同的时间点可以定义为时间戳。

已经提出了几种可视化技术来直观地分析这种特定类型的数据。传统的二维图是一种广泛使用且众所周知的视觉表示形式，可用于可视化地标位置处的属性。可以通过投影来包含时间信息（例如，使用颜色或线宽）。另一种方法是将二维表示扩展到三维以显示时间。在这种情况下，三个数据维度被映射到三个空间维度。在这种情况下，最简单的表示是 3D 曲面图，将属性值随时间变化连接起来。三维时间数据的另一个突出且广泛采用的视觉表示是时空立方体 [6]。最初，它使用二维来显示二维空间信息（例如地图数据），使用第三维来可视化时间；基本上沿着时间轴级联几个二维图[7]。时空立方体的概念还可用于显示随时间变化的地标处的属性，其中每个数据维度由三个空间维度之一编码。

旋转、缩放和平移等交互是探索三维数据的重要概念。我们利用它们，并在此提出了一种用于分析 3D 数据的 2.5D 图的新概念，其中时间是交互的问题。从传统且众所周知的 2D 绘图开始，通过使用 3D 旋转改变观察方向，相继显示更多时间信息。这是通过使用椭球模型而不是笛卡尔坐标系来实现的。与现有技术相比，椭圆体模型允许弯曲空间以查看时间。这种弯曲直接受到观看方向的影响，而观看方向由用户控制。我们将这种新的可视化技术称为弹出图（PP），其灵感来自于著名的弹出贺卡。如果这样的卡片关闭，它是平坦的（不显示时间），但是当打开时，连续更多的结构（时间）变得可见。

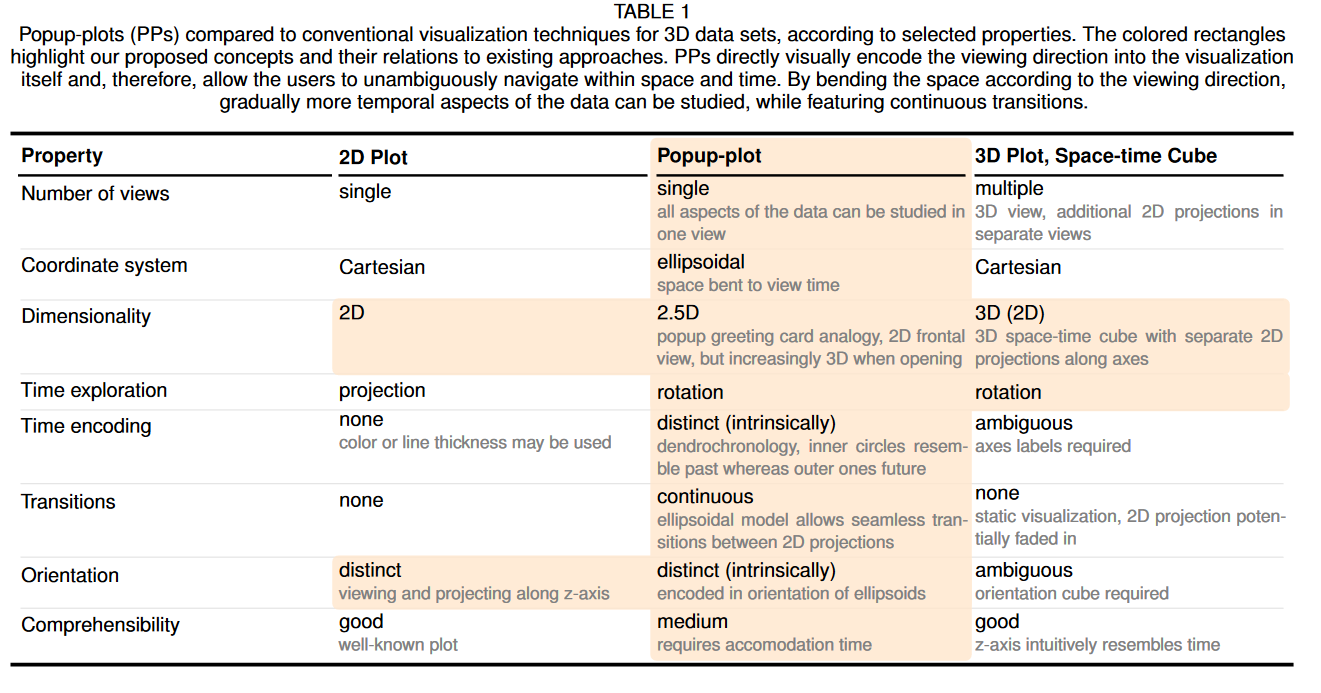
弹出图（PP）使我们能够将各个方面固有地编码到可视化中，并通过简单地改变观察方向来研究数据的不同方面。因此，PP 允许在一个视图中检查数据，而无需使用投影、多个视图或刷动和链接。由于空间弯曲，可以通过查看可视化的形状来推断数据的当前查看方向。椭球模型在视觉上对时间信息进行编码，类似于树的年轮，其中内环类似于过去。此外，解析椭球模型提供了不同观察方向之间的无缝过渡。表 1 概述了传统可视化技术与我们提出的 PP 之间的差异。

我们在第 2 节中概述了相关的最先进技术。第 3 节中描述的弹出图 (PP) 的新颖概念已作为基于 Web 的应用程序实现（参见第 4 节） 。为了证明弹出图（PP）的多功能性，我们将它们应用于两个数据集，一个来自医学，另一个来自流量分析（参见第 5 节）。这项工作在第 6 节中进行评估，并在第 7 节中进行讨论。我们在第 8 节中对未来的方面进行总结。

2 相关工作

为了涵盖我们工作的所有方面，我们必须参考有关可视化的几个领域。最突出的是时间数据可视化和时空数据可视化，其次是交互技术。由于我们的用例基于医疗数据和交通数据，因此我们随后对这些学科中的数据可视化方法进行回顾。

时态数据可视化描述了允许分析时态数据集的可视化系统和技术。现有的时态数据可视化应用程序非常异构，因为它们是为了解决不同领域内的各种任务而开发的。 Aigner 等人对时态数据可视化进行了全面的调查。 [2]。许多技术使用线性隐喻（即时间线）将时间可视化为连续变量。例如，ThemeRiver（Havre 等人[8]）和堆叠图（Byron 和 Wattenberg [9]）沿水平时间轴绘制属性值。此类应用程序对于探索属性随时间的变化以及研究单个时间戳内属性的关系非常有用。这同样适用于沿线性时间轴以成对方式连接相关信息的弧线图[10]。循环图采用时间的水平表示来描绘单变量 [11] 和多变量 [12] 时间序列数据中的循环模式。托明斯基等人。 [13]使用线性表示在时间轮中显示时间，但建议围绕时间轴以圆形布局排列属性。托明斯基等人。 [14]后来将该技术扩展到三个维度。

其他方法也使用第三维来编码可视化中的附加信息。 Timetunnel，由 Akaishi 和 Okada [15] 提出，以 3D 扇形方式围绕中央时间条定位 2D 绘图。流可视化中的隐喻可用于显示属性随时间的变化 [16]，传达故事情节的演变 [17]，或将属性解释为 3D 对象 [18] 以显示其时间进程。更复杂的结构（例如 Noirhomme-Fraiture [19] 的变焦星）可用于包含附加信息（例如直方图），以便对数据进行更详细的分析。

由于线性时间轴在较大数据集的情况下可能会消耗大量空间，因此已经研究了径向布局以有效地传达时间信息空间。通过使用颜色[20]或分层方法[21]，可以观察属性随时间的变化。韦伯等人。 [22]提出了一个图，其中属性沿着显示时间进程的螺旋可视化。最近的方法采用更复杂的几何变换来显示时间信息。巴赫等人。 [23]使用基于曲线的布局来表示可视化中的时间。其他作者利用平行坐标并找到了通过合并时间信息来增强绘图的新方法。格伦德尔等人。 [24]提出了一个小部件来探索并行坐标图中的时间并比较两个连续轴之间的时间关系。约翰逊等人。 [25]使用深度线索来整合平行坐标中的时间。通过这种方式，可视化可以在关注属性时揭示数据中的时间模式。

我们使用新颖的曲线布局来显示时间，这取决于观察方向，这意味着球形或椭球体模型。这不仅提供了以与传统和广泛采用的绘图相同的方式探索数据的可能性，而且还提供了通过改变观看方向或更一般地通过交互来探索时间。此外，不同数据视图之间的无缝转换可以评估一个视图内的时空关系。我们的方法类似于由Zhao等人提出的环图。 [26]，将时间编码为环。通过显示与 2D 视图交织在一起的 3D 视图，可以探索数据中的模式。然而，环图不会根据视角而改变，因此时空仍然是平坦的。

由于时间数据通常与空间位置相关，因此这两个术语的组合导致时空数据的可视化[27]。我们提出的可视化技术也可以应用于一维时空数据集[28]。然后，第一因变量表示空间（例如，沿路径的一维位置），第二因变量定义在这些空间位置测量的属性。时空立方体是可视化此类数据的直观且广泛的概念[29]。作者描述了沿每个轴投影和展平的方法以及提取和转换操作。与我们提出的技术相关的操作是弯曲和展开。

与我们的概念的主要区别在于，时空立方体考虑平坦时空，空间和时间之间具有不连续的过渡。然而，在时空数据的配置中[30]，例如，当将地理地图作为两个依赖属性时，我们的方法将不会类似于令人满意的视觉表示。因此，我们的方法不适用于完整分析这些数据。

交互技术支持对时空数据的理解。处理多维数据的典型方法是在多个视图中呈现数据的不同方面[31]。我们专门设计了我们的方法，使用户可以在一个视图中直接与三维图进行交互，以研究数据的不同方面。这是通过隐含时空椭球模型来实现的。空间折叠已经被其他方法所应用。埃尔姆奎斯特等人。 [32]提出了一种折叠空间以在探索过程中保留上下文和概览的技术。当空间弯曲将二维地图延伸到三维时，人们会得到折叠空间范围的印象以及两点之间距离的概念。同样，我们对空间进行变形，以实现不同观看视角之间的无缝过渡。 van Wijk 和 Nuij [33] 描述了对地图上两点之间的行进距离进行编码的另一种方法。他们在过渡过程中使用了距离与相机速度和高度的非线性映射。

由于我们的 PP 根据观察方向延伸到三维，我们还对数据点应用非线性（椭圆体）映射，以实现平滑和无缝的过渡。与 Azuma 等人类似。 [34]我们建议根据需要更改可视化的表示，但在我们的例子中取决于当前的观看方向。科尼哈等人。 [35]介绍了一种在多视图环境中研究曲线族的方法。对属性随时间的时间进展的分析也可以解释为研究一组曲线。我们提出的方法允许通过 3D 交互来研究属性值。

医疗应用程序以不同的方式利用时间和时空数据可视化。医学上的时间进展通常是指一名或多名患者的病史，以研究模式[36]或事件[37]。在这种情况下，事件带有时间戳但离散，并且通常无法随着时间的推移在特定地标处连续监控。因此，事件可视化并不直接适用于我们的时态数据类型。在其他情况下，时空可视化技术用于描述测量数据的时间变化。 De ́ anBen 等人。 [38]使用多个视图来显示心血管动力学的时间进展。他们同时使用 2D 图形和 3D 渲染图像。曹等人。 [39]关注的是测量间隔并不总是在简单的线图中显示的事实。格拉瑟等人。 [40]使用平行坐标向三维的扩展来表达纵向灌注磁共振研究中的时间。在他们的可视化中，可以清楚地识别描述肿瘤边界局部异质性的峰值。我们的方法可用于研究在局部感兴趣点进行的医学测量的时间进展。

交通数据包含多种不同的可能数据类型，包括空间中移动的物体的采样位置，以及汇总研究，例如沿特定路线的物体数量。收集这些数据用于统计评估或实时监控交通状况[41]。时间是一个重要方面，因为交通状况通常在一天或一年内变化很大。交通数据可视化的主要研究目标是通过提供合适的解决方案[28]（如交互、聚合和内存管理方法）来分析大量数据。还有其他方法专注于分析交通系统中特定路线沿线的参数。托明斯基等人。 [42]实现了时空墙，用于分析随时间变化的轨迹的属性。格罗特尔等人。 [43]采用不同可视化技术（即平行坐标和热图）的组合来分析轨迹。我们的方法可用于可视化沿着预定义轨迹（例如火车轨道或高速公路）的属性的时间进程。

3 弹出图

弹出图 (PP) 描述了一种新颖的 2.5D 类型的图，用于时态数据的可视化。我们使用 3D 椭球模型来代替笛卡尔坐标系来显示数据，这在 3.1 节中有详细解释。 PP 通过根据当前观察方向连续添加时间信息来扩展传统的 2D 绘图。 PP 的概念允许我们在单一视图中查看数据并与之交互。

PP 可应用于由三个数据维度组成或可投影到三个数据维度的数据，其中一维类似于时间。在本文中，我们处理的 3D 数据集由由两个因变量（属性、地标）和一个自变量（表示时间戳）定义的数据点组成。椭球模型为每个数据点分配一个 3D 位置。因此，PP 提供了一种在 3D 空间中绘制数据点的新颖概念，其中 3D 旋转用作交互机制，从不同角度研究数据。现有的可视化技术也适用于点图和线图，可以用于增强视觉表示（例如，通过添加 viewcube [44]）。由于 PP 的椭球模型主要描述数据点如何变换，因此它不限于任何特定的可视化技术或应用领域。 3.2 节概述了数据的视觉表示和交互概念。

3.1 椭球模型

PP 采用椭圆体模型将数据点映射到 3D 位置。随后，我们解释了数学背景并介绍了该模型的理论概念。我们用二次曲面来模拟时空，例如椭球体和双曲面。在本节中，我们使用球坐标表示法，其中几何点由三元组 (r, θ, φ) 描述。我们进一步提出 PP 的内在和外在观点。内在视图显示从用户角度使用 PP 可视化的数据，从而产生一个椭圆弯曲的坐标系，其原点从笛卡尔 xy 平面连续向外移动。相反，外部视图从固定的观察者角度展示了嵌入笛卡尔坐标系的转换后的数据。应该注意的是，所有附图都是通过在矢量图形语言 Asymptote 中实现并程来实现的 [45]。

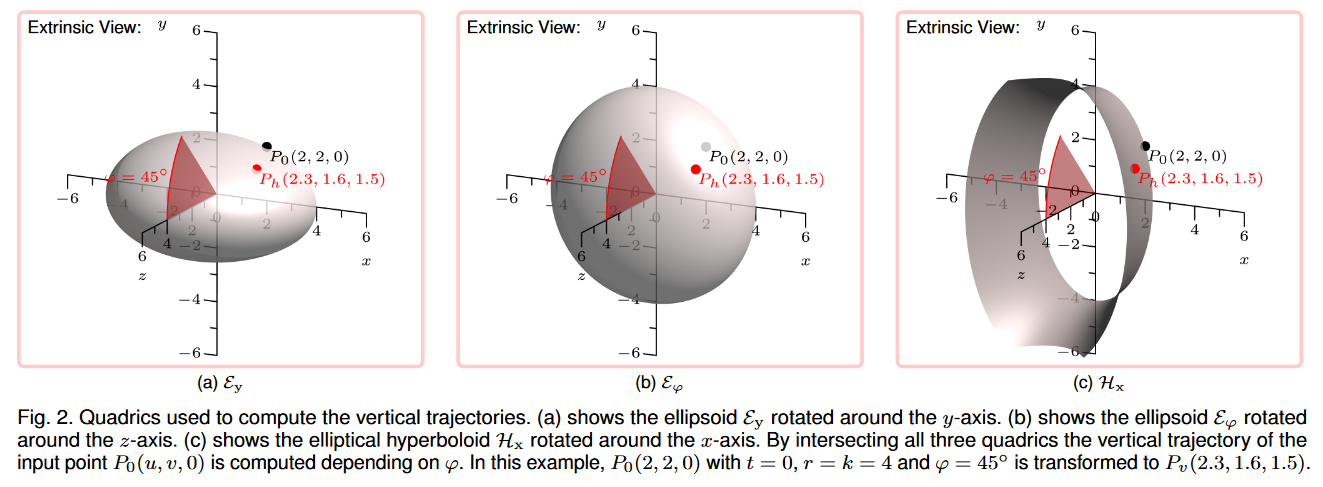
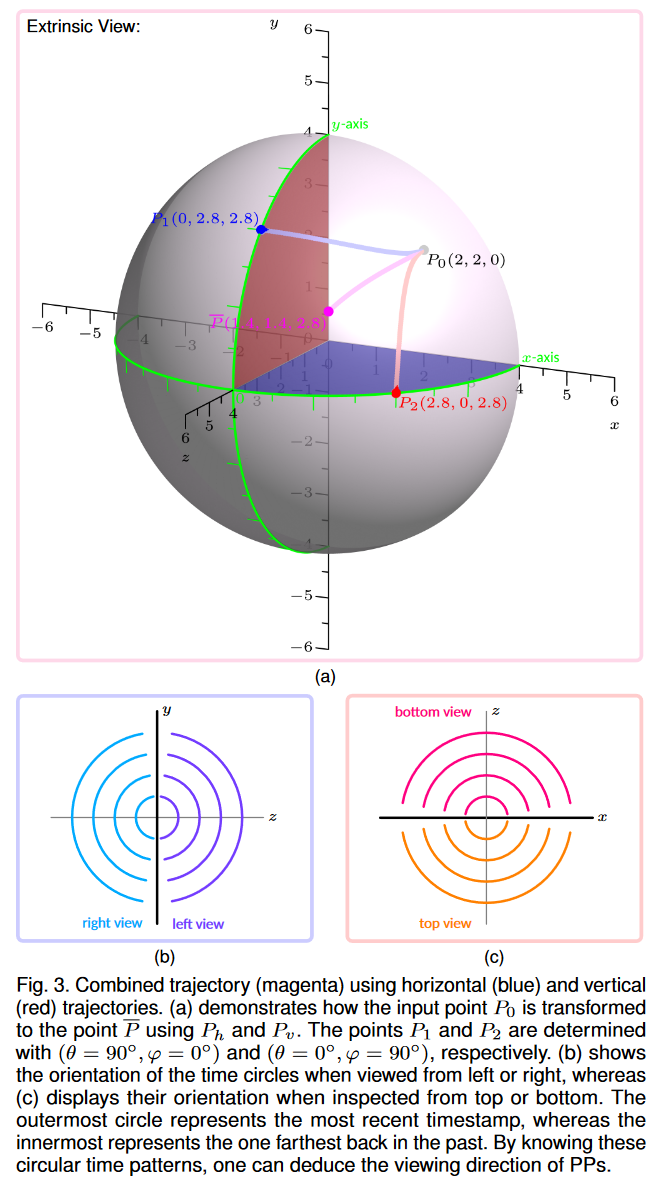
PP 中的主要交互概念是 3D 旋转。因此，为用户提供了两个自由度 θ 和 φ，分别类似于从左到右和从上到下的视角。不同的视角设置将导致数据以不同的方式可视化。同一数据点的所有可能的 3D 位置都被汇总为轨迹。水平观察方向由 θ 控制，改变 θ 时生成的数据点的 3D 位置集合称为水平轨迹（参见第 3.1.1 节）。类似地，φ 引导从上到下的观察方向，因此我们将改变 φ 时生成的一组数据点 3D 位置称为垂直轨迹（参见第 3.1.2 节）。最初，数据点的轨迹是针对两个视角分别确定的，但随后组合成单个连续轨迹（参见第 3.1.3 节）。由于时间是沿着朝向观察者的正 z 轴编码的，因此我们只考虑正半空间并使用 xy 平面剪切所有二次曲面。

3.1.1 水平轨迹

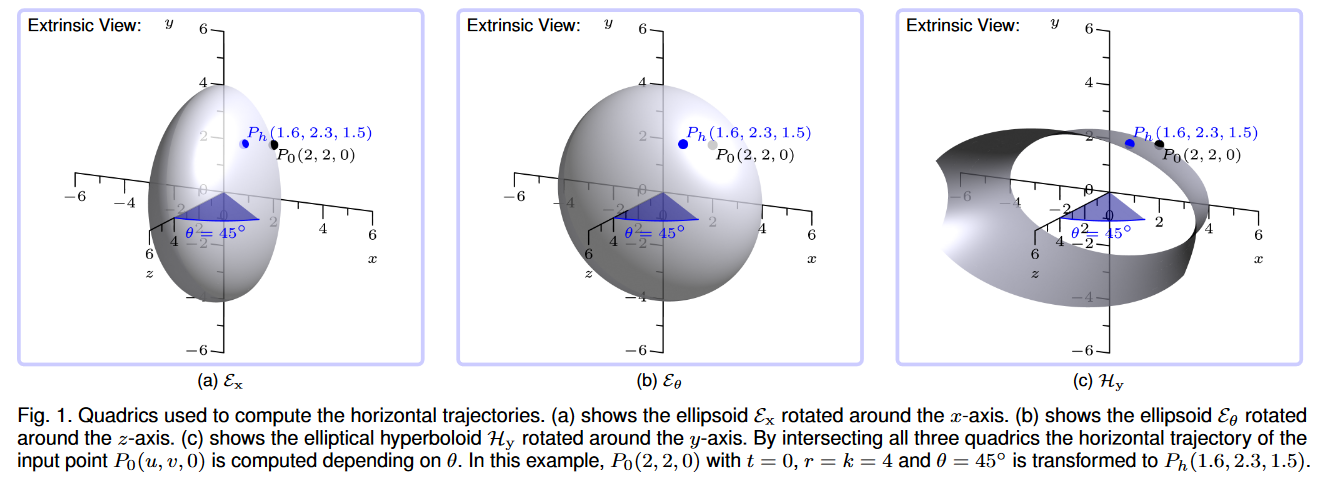
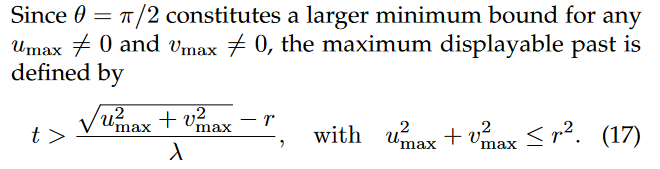
3.1.2 垂直轨迹

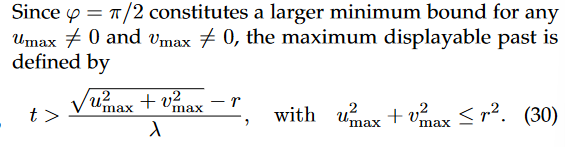
3.1.3 组合轨迹

3.2 视觉映射与交互

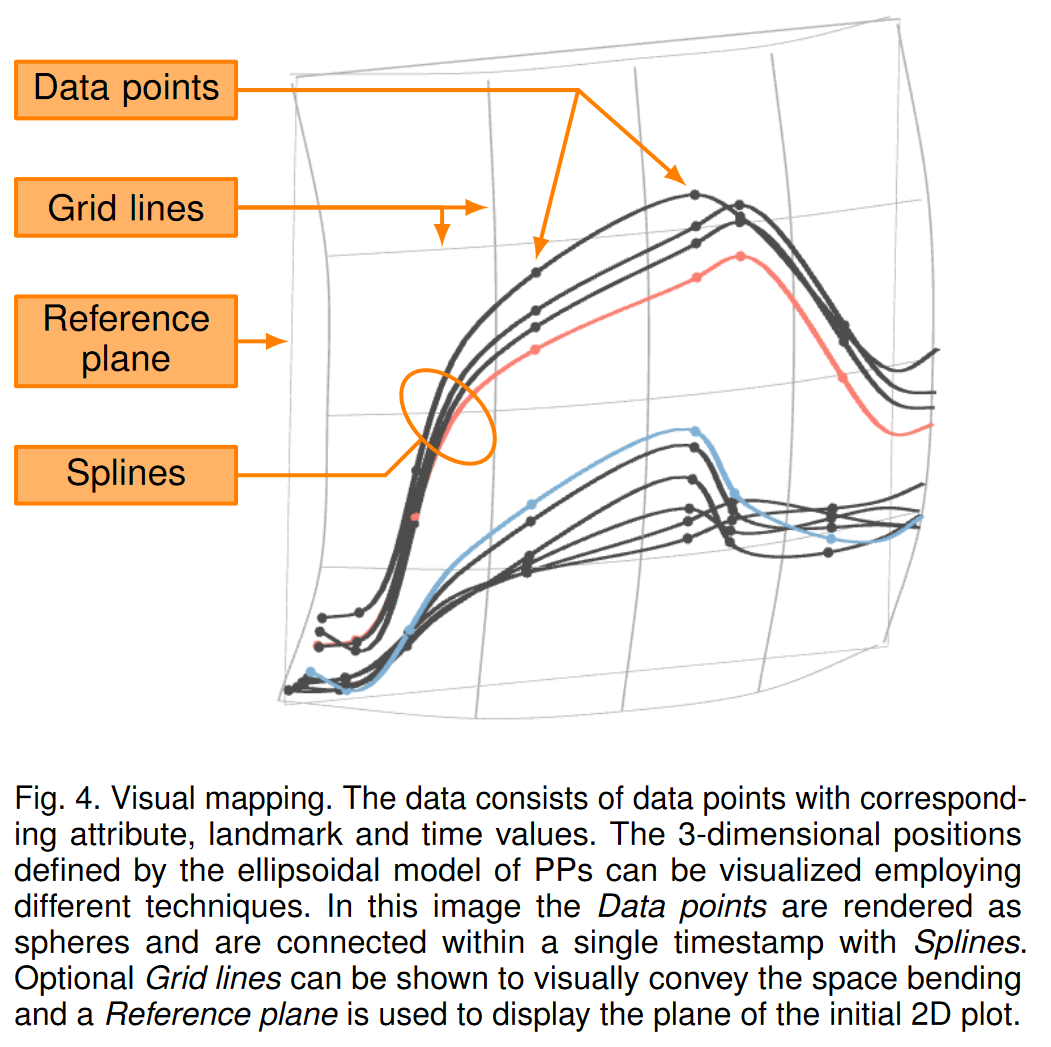
椭球模型根据观察方向定义 3D 数据点的位置。该模型确保不同观看视角之间的连续无缝过渡。因此，PP 提供了一个在三个维度上显示数据的基本框架，然后可以通过采用现有的可视化技术来丰富该框架。以最简单的形式，我们建议在可视化中将数据点呈现为球体。我们进一步建议将同一时间的转换数据点连接到连接曲线，例如，通过使用 Catmull-Rom 样条线。随后，对这些样条线进行等距采样，并将获得的位置用于渲染。图 4 概述了这些提出的视觉映射策略。

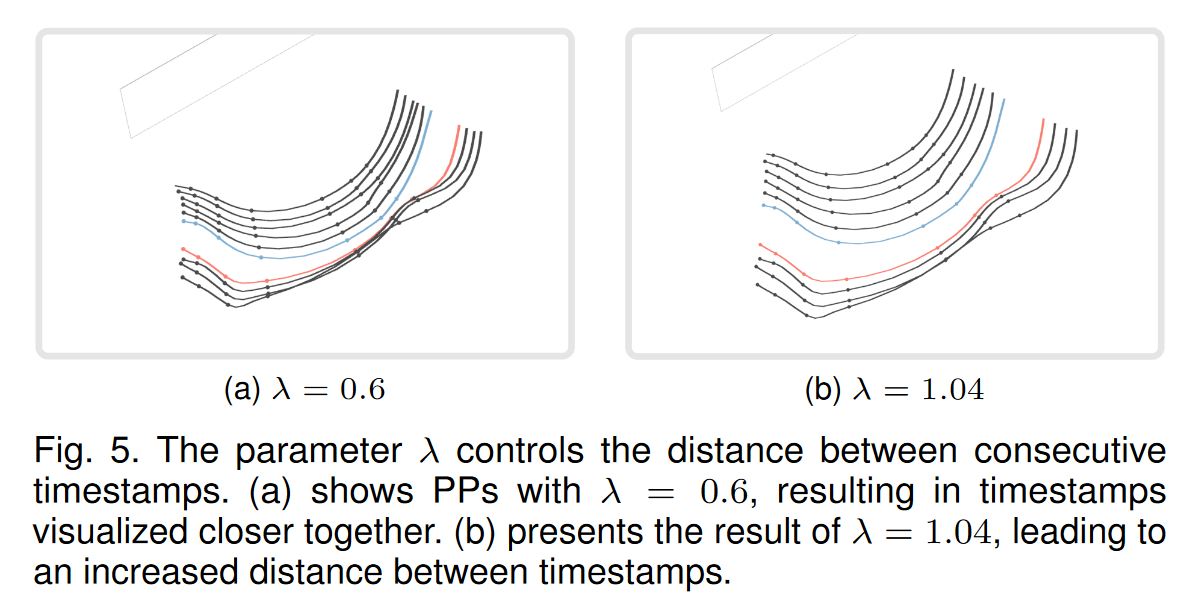
PP 可视化会受到参数 λ 和 r 的影响。时间戳之间的距离由 λ 控制（见图 5），允许用户放大和缩小 PP。不同的 λ 设置也使得 PP 能够适应各种类型的数据集，甚至是不同时间跨度的数据集。椭圆体模型的半径 r 定义了绘图的大小和可显示时间戳的数量（即最大可显示过去，请参见公式 17 和公式 30）。

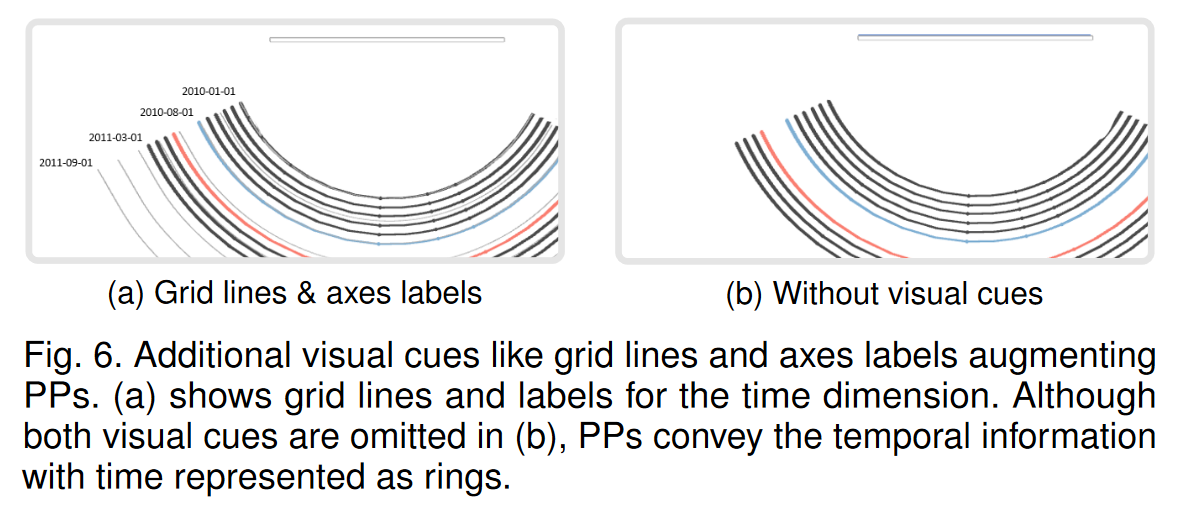
除了旋转之外，我们还测试了进一步交互的可能性来分析数据。可以在可视化中显示网格线和标签（参见图 4），以更好地传达上下文信息。网格线的形状和位置也是根据PP模型计算的。由于当前的观看方向定义了可视化的形状，因此，还可以在不阅读标签或解释网格线的情况下解释 PP（参见图 6）。相反，当使用时空立方体等传统技术时，人们总是需要参考线索才能解释可视化。我们还添加了通过单击按钮快速选择预定义数据视角的可能性。这些视角之一是传统的 2D 图，由 θ = 0°、φ = 0° 定义。另外两个视角是从顶部（θ = 0°，φ = 90°）和从侧面（θ = 90°，φ = 0°）查看数据。 PP 不限于这些预定义的设置，其他预定义的视角可能有助于强调数据中的某些模式。我们还添加了通过单击各自的 3D 样条曲线来选择各个时间戳的可能性。然后，所选时间戳的更多详细信息（即日期和最小/最大属性值）将显示在单独的窗口中。不同的时间戳可以通过其分配的类别颜色在视觉上区分。为了一般性，我们没有包含任何进一步的类别语义。类别可以映射到数据中特定领域的语义组（例如，通过聚类识别）。

PP 方法涵盖了时态数据可视化所需的许多方面（表 1 中介绍）：

观看次数。 PP 只需要一个视图即可传达数据集的所有方面。数据的不同视图并不代表在单独窗口中显示的封装状态，而是通过用户直接与数据交互来实现。
坐标系。数据点的位置根据PP椭球模型计算。可以识别属性值随时间显着变化的地标以及时间变化较小的地标。
维度。根据椭球模型，PP 采用 2.5D 数据表示。可以通过 3D 旋转来实现对数据的进一步探索（其中还包含时间）。每次旋转都会揭示数据的不同方面。
时间探索。从侧面观察（θ = 90 且 φ = 0）时，会显示属性的时间进程。可以看出随着时间的推移，属性值是否持续增加或减少。当从顶部查看 PP（θ = 0 和 φ = 90）时，会显示时间戳的数量和距离。
时间编码。时间戳根据树木的年轮进行编码，过去的时间点位于内部。这种时间的循环编码可以非常快速地识别较旧和较新的时间戳。人们可以识别时间戳是否大部分是等距的，或者它们之间是否存在较大的间隙。循环时间编码表现出固有的时间顺序。
过渡。 PP允许用户在3D空间中自由旋转。在旋转过程中，PP 椭球模型保证了变换后的数据点位置的连续转变。与数据集交互时看不到跳跃效果。
方向。这解决了 PP 的一个非常重要的方面，因为数据集的当前方向始终直接由可视化本身反映。这允许立即探索数据，而无需任何额外的视觉提示（例如，方向立方体）。
可理解性。由于 PP 会弯曲空间以显示时间，因此可能需要一个初始适应阶段来理解该概念。尽管如此，PP 提供了探索和解释数据的丰富可能性。

4 实施

PP 是使用 JavaScript 和 WebGL 进行渲染的基于 Web 的解决方案。 2D 数据集存储为 JSON 格式的文本文件。我们使用 ThreeJS (v. r84) [46] 来渲染，并使用 JQuery (v. 3.2.0) [47] 来实现用户界面元素。我们的方法在配备 Intel Core i7 2.90GHz 处理器、16 GB RAM 和 NVIDIA GeForce GTX 670M 显卡的系统上进行了测试，并在 Windows 8.1 64 位上使用网络浏览器 Firefox（v. 52.0.2）。数据集的加载只需几毫秒，并且交互是实时运行的。对于我们提出的两个用例，该应用程序消耗了大约 300 MB（参见图 7 和图 8）。

5 结果

这项工作是由来自不同领域的两个用例推动的。两个用例的数据结构都适用于我们对包含两个因变量和自变量时间的 3D 数据集的定义。随后，我们解释了如何使用 PP 来探索这些数据。

第一个用例属于医疗领域，与称为主动脉夹层 (AD) 的血管疾病有关。通常，在健康的血管中，血液在单个流动通道内流动。在 AD 的情况下，会形成几个其他流动通道，导致容器直径和压力增加。由于这些通道并不是为了承受高血压而设计的，它们最终往往会破裂，这是一种致命的事件。血管直径是预测此类事件的重要指标。因此，主动脉直径（属性）是在特定测量点（标志）处评估的。这些测量必须在多次患者检查（时间戳）中重复进行，以监测患者的健康状况[48]。在我们的用例中，检查了接受手术治疗以缩小主动脉直径的患者的数据集。 3D 数据集由十个时间戳组成，这些时间戳是在七年的时间内采集的。主动脉直径是在主动脉沿线的 11 个标志处测量的。使用两个类别来识别手术干预之前（蓝色）和之后（橙色）的时间戳（见图 7）。

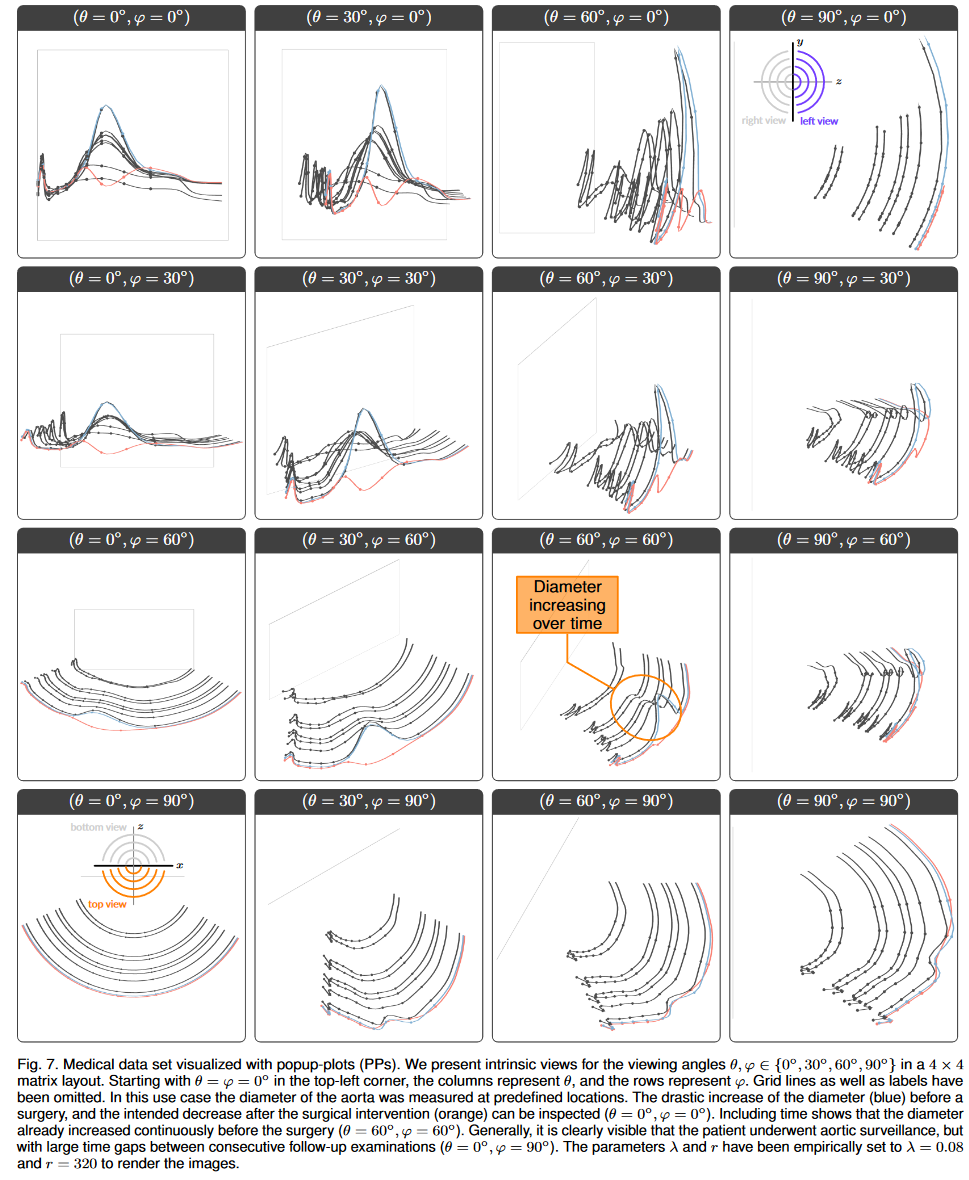
在中心标志处可以检查相当不同的直径值（θ = 0°，φ = 0°），而在外部标志处，直径随时间保持恒定。在手术干预之前可以看到最高直径值（蓝色）。当分析中包含时间时，我们可以认识到直径的急剧增加是最近发生的（θ = 60°，φ = 60°，直径随着时间的推移而增加）。手术干预后立即对患者进行监测，由非常靠近的蓝色和橙色时间戳表示。橙色时间戳还显示了中间区域直径的预期术后减小（θ = 30°，φ = 60°）。当查看时间戳（θ = 0°，φ = 90°）时，可以清楚地看到患者接受了定期医疗监测，但检查之间的距离不同。由于中心区域的直径值相当低，两个时间戳描述的直径值不同于数据集的其余部分。可以看出，这两个时间戳描述了过去发生的检查（θ = 30°，φ = 30°）。图 7 中采用的矩阵视图也可能包含在医疗报告中，以直观地传达时间和时间变化。

第二个用例与交通数据有关。在大城市的街道网络中，有所谓的主动脉路线，它们对于整体交通状况非常重要。这些路线可能是进出城市的高速公路或高速公路，或者绕开城市以引导周围的交通。该用例的 3D 数据集包含沿着主动脉路线（穿过大城市的高速公路）行驶的车辆（汽车和卡车）数量。车辆数量（属性）在计数站（地标）自动记录。我们选择了 24 个记录，代表 2014 年一天的 24 小时（时间戳）。我们的 PP 结果如图 8 所示。

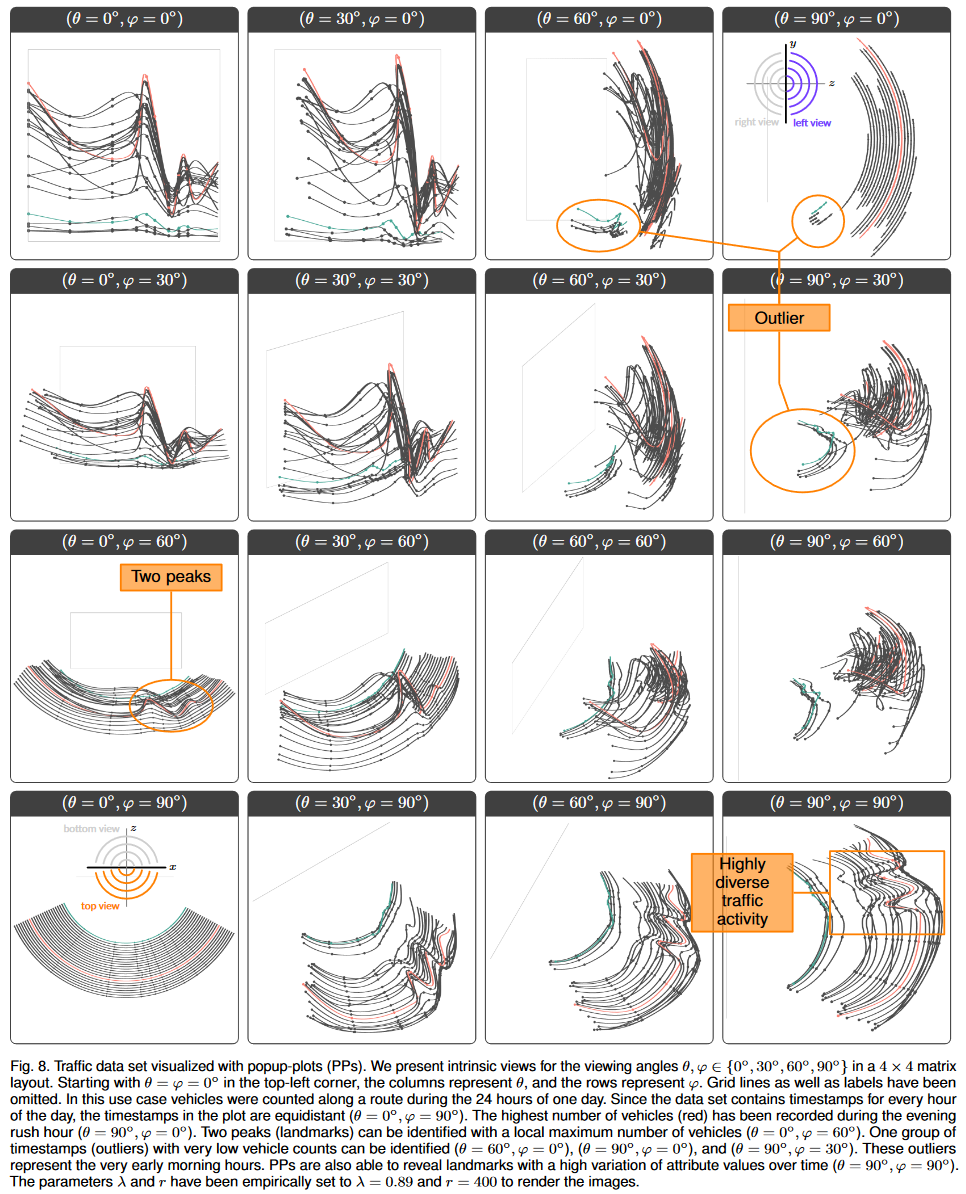
数据中可以识别出两组（θ = 0°，φ = 0°），其中一大组时间戳记录了相当高的流量计数，而一组异常值由四个时间戳组成，属性值较低。我们将车辆数量最多的时间戳标记为红色，将离群值组的一个时间戳标记为青绿色。当旋转绘图查看时间时，可以看到离群值组（Outlier）代表凌晨时段（θ = 60°，φ = 0°）、（θ = 90°，φ = 0°），并且（θ = 90°，φ = 30°）。据报告，晚高峰期间的交通量最高（θ = 90°，φ = 0°）。从侧面查看数据，早晚高峰时段清晰可见。还可以看出，车辆数量在早上（一小时内）急剧增加，但在傍晚和夜间时间缓慢减少。数据中的局部最大值表明，特别是两个地标在高峰时段报告了高车辆数量（两个峰值）（θ = 0°，φ = 60°）。该数据集包含一天中每小时的流量计数，因此时间戳都是等距的（θ = 0°，φ = 90°）。数据的中间视图（θ = 90°，φ = 90°）揭示了一些地标的交通计数随时间的变化（高度多样化的交通活动）。车辆数量在夜间保持相当恒定，但在白天发生变化。可以通过旋转 PP 来分析数据中的此类模式，而无需创建额外的孤立视图。

这些用例展示了 PP 如何允许研究数据的不同方面。从传统的二维图（θ = 0°，φ = 0°）开始，通过旋转可视化来查看时间。当从左侧或右侧观察时（例如，θ = 90°，φ = 0°），连续时间戳与最小和最大属性值之间的距离是可见的。这些视图呈现了数据的时间发展，时间按圆圈排列。在 PP 的顶部或底部视角（例如，θ = 0°，φ = 90°）中，时间再次被描绘为圆圈，并且地标的位置是可见的。这些视图中未描述属性值。 θ 和 φ 的其他值保证了不同视点之间的无缝过渡。

6 评估

我们进行了一项用户研究，以评估 PP 在分析数据时的潜力。我们的研究包括来自不同领域的 15 名参与者，如软件开发人员、放射技术专家、统计学家和计算机科学家。关于 3D 可视化参与者的专业水平，八名受访者表示拥有丰富的经验，四名受访者表示拥有一些经验，三名受访者表示几乎没有经验。用户研究已以基于网络的形式实施。单个评估表的平均完成时间在 8 至 15 分钟之间。

我们的研究将 PP 与众所周知的时空立方体概念进行了比较。由于PP提出了一种新颖且创新的概念，并不能立即与既定的接口标准相匹配，因此早期阶段的评估很难设计[49]。因此，我们特意以通用的方式设计了用户研究，以防止评估偏向特定领域。在用户研究开始时，每个参与者都会收到有关该主题的简短在线介绍，其中包括一些如何解释 PP 和时空立方体的建议。在线介绍由一页内容组成，其中包含描述 PP 主要特征的文本以及补充文本的插图，其中使用人工数据集来绘制图表。由于用户研究是在线完成的，因此用户可以花尽可能多的时间进行在线介绍。随后，他们被要求完成三项任务：

T1 从不同的观察方向识别数据。
T2 描述时间关系。
T3 识别数据中的异常值。

任务 T1 特别涉及方向和转换（回想表 1）。首先，参与者必须跟踪视频序列中的数据峰值，其中时空立方体和 PP 在三个维度上旋转。其次，他们必须在数据峰值的最后位置放置一个圆形标记。任务 T2 解决时间编码问题（回想表 1），以便推断两个不同时间戳之间的时间关系。在可视化中，两个时间戳用不同的颜色标记，参与者被要求选择较早的时间戳。在任务 T3 中，参与者被要求检测数据中的异常值。异常值之前被定义为与数据集的其余部分表现不同的数据点。参与者可以通过用鼠标绘制区域来标记异常值。只能绘制一个区域，绘制新区域会自动删除旧区域。任务 T3 旨在测试是否可以以探索性方式使用 PP 来搜索数据中的重大变化或模式。

PP和时空立方体的所有任务都必须完成。我们为每个任务交替使用时空立方体和 PP 的顺序。对于任务 T2，PP 和时空立方体使用了不同的颜色，以避免任何相关性。对于每个给定的答案，参与者必须按照 11 点李克特量表对自己的信心进行评分。该研究的实施方式是从可视化中省略参考尺度（例如轴标签），以最纯粹的形式比较两种可视化。对于 PP，仅将 2D 图的平面绘制为线框，对于时空立方体，仅将周围的立方体绘制为线框。通过这种配置，我们测试了参与者是否能够正确解释 PP 可视化的椭圆体形状，即使在没有网格线和标签支持的情况下也是如此。

我们使用不同的人工创建的 3D 数据集进行用户研究。对于任务 T1，我们生成了一个与医疗用例类似的 3D 数据集（参见第 5 节），具有非等距时间戳和九个地标。在两个地标处，属性值随着时间的推移而增加。对于任务 T2 和 T3，我们创建了一个与交通用例类似的 3D 数据集（参见第 5 节），具有等距时间戳和 10 个地标。该数据集包含两个簇，随着时间的推移，一个簇的属性值较低，另一个簇的属性值较高。

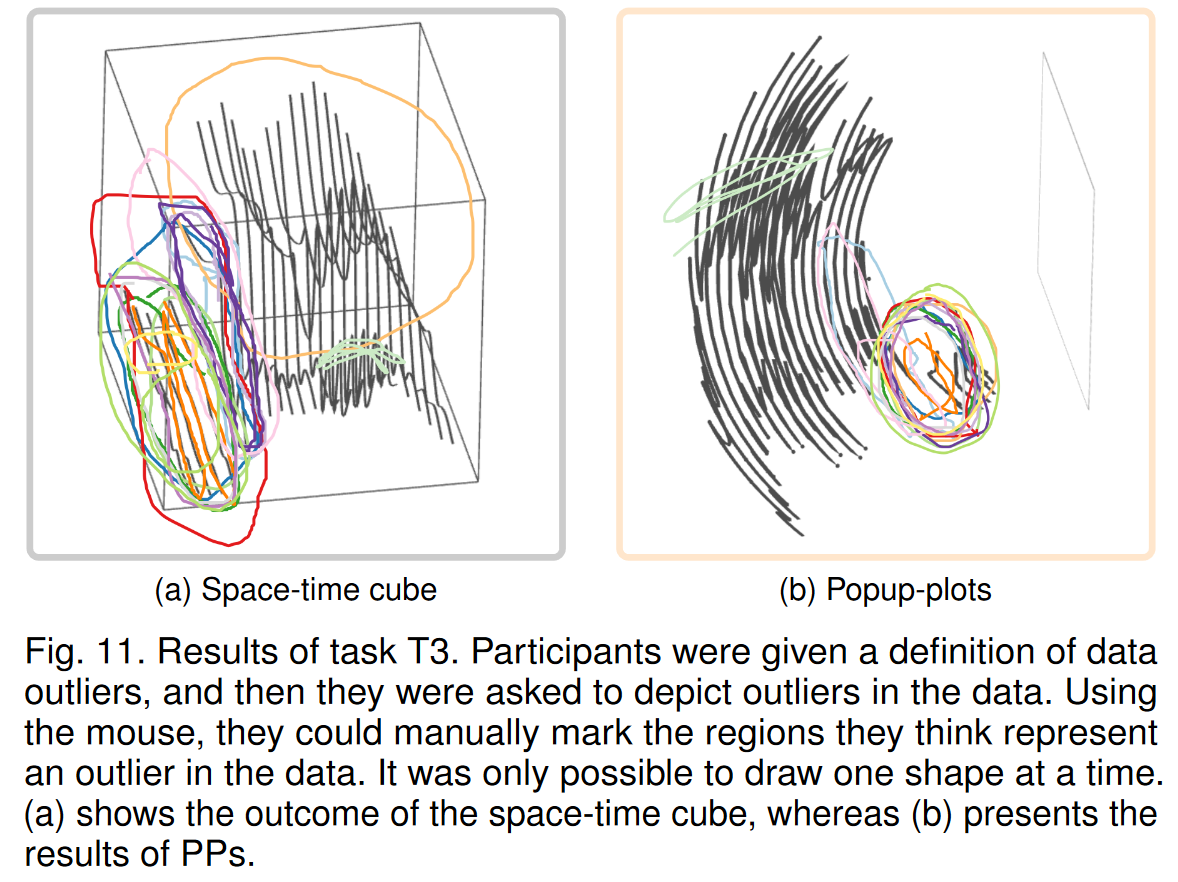
通过对覆盖数据峰值最终位置的标记进行计数来计算命中率和未命中率来评估任务 T1（参见图 9）。我们遇到的时空立方体的命中率为 9，而未命中率为 6。PP 的命中率为 14，未命中率为 1。标记位置如图 9 所示。参与者较少与 PP (9.60 ± 1.06) 相比，使用时空立方体 (8.67 ± 2.53) 时对放置标记更有信心。造成这种情况的原因之一可能是 PP 的无缝过渡，使参与者能够更好地在视觉上跟踪峰值。第一项任务的结果表明，所有参与者都能够正确解释 PP 的弯曲时空表示，并在旋转绘图时正确遵循无缝过渡。

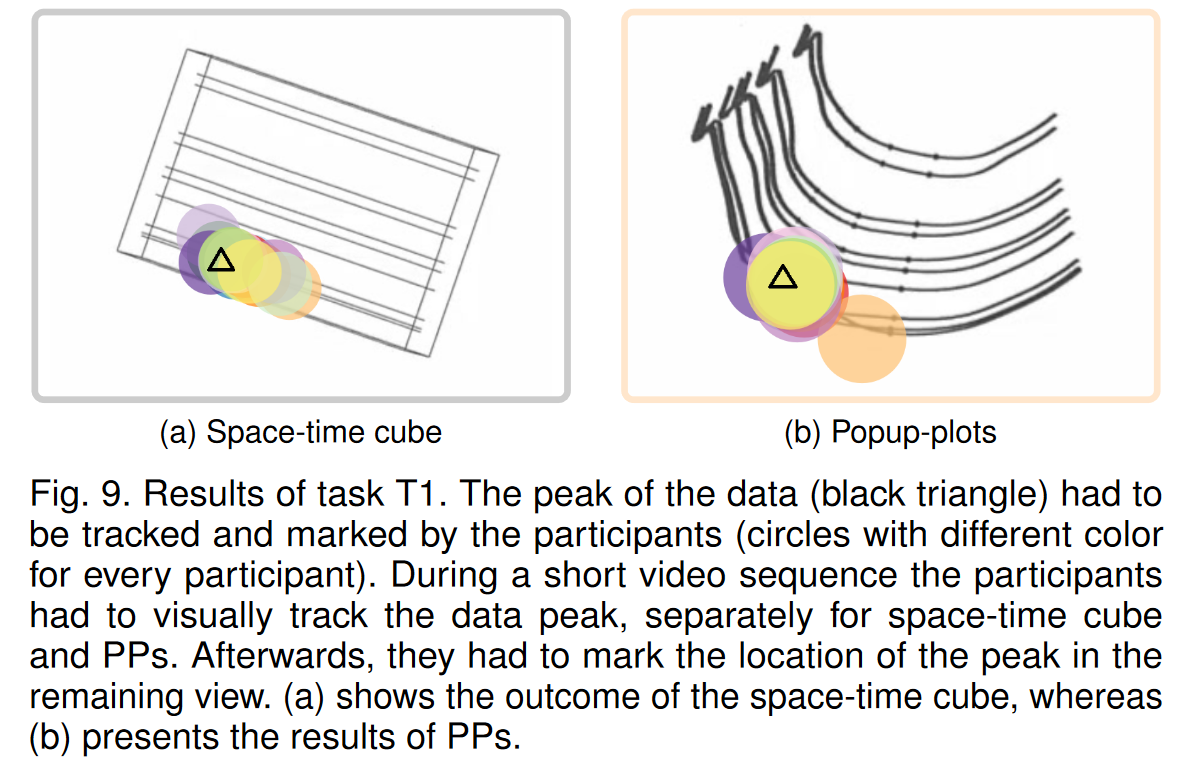
在任务 T2 中（见图 10），七名参与者进行了猜测（正确率 43%），八名参与者选择了“我不知道”时空立方体。出现这种结果的原因可能是时空立方体没有最纯粹形式的时间编码，这得到了置信率 (6.80 ± 2.83) 的支持。对于 PP 可视化，14 名参与者 (93%) 正确选择了较早的时间戳，只有 1 名参与者 (7%) 选择了错误的时间戳；参与者也非常有信心（9.73 ± 0.59）。 PP 的结果表明，即使没有标签或网格线，参与者也能够正确地将时间的视觉表示解释为环。因此，PP 的概念似乎很容易理解，即使对于还不熟悉它的用户来说也是如此。

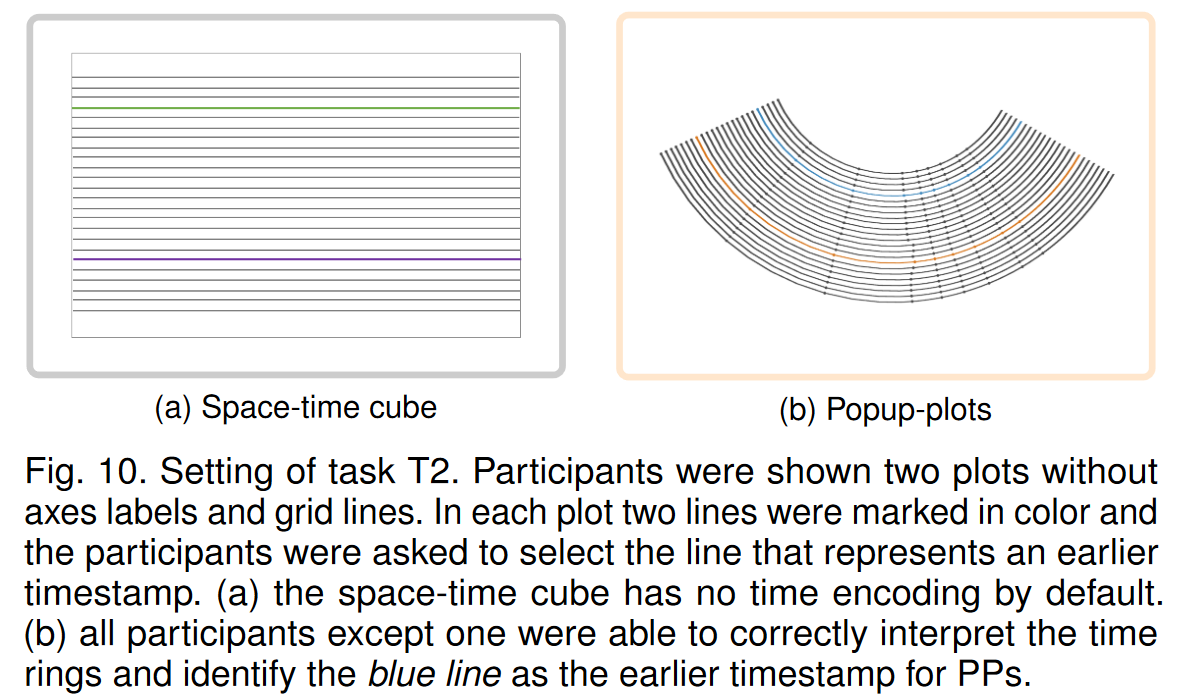
对于任务 T3（参见图 11），我们计算了标记区域的边界框和数据中簇的边界框。准确度定义为标记区域与正确离群区域相比的 Jaccard 指数 [50] 的平均值。时空立方体的结果为 (0.54 ± 0.29)，PP 的结果为 (0.66 ± 0.15)。并非所有参与者都能正确回答，并且在某些情况下，参与者选择的区域完全超出了实际异常值区域（两个用于时空立方体，一个用于 PP）。时空立方体 (6.53 ± 3.20) 和 PP (7.40 ± 3.40) 的置信率支持了这一相当平均的结果。然而，结果表明，PP 可以在探索性环境中使用，以搜索数据中有趣的模式。

我们通过将参与者分为两组来进一步评估任务 T1-3 的结果。第一组 (G1) 由已经熟悉 3D 可视化，特别是时空立方体的人员组成（8 名参与者）。相比之下，第二组 (G2) 包括没有任何 3D 可视化经验的参与者（7 名参与者）。 G1 组的参与者对所有三项任务的答案表现出稍高的信心，例如，G1 组的 PP 为 (5.33 ± 3.53)，T1 中的时空立方体为 (5.13 ± 3.44)，而 G1 组的参与者则为 (4.27 ± 3.58)。对于 PP，对于 G2 组的 T1 中的时空立方体，为 (3.53 ± 3.62)。可以看到，使用 PP 时置信度的小效应量（Cohen’s d [51]）为 0.30，而在 T1 中使用时空立方体时，置信度的效应量小为 0.45。这两组之间的结果没有显着差异。例如，任务 T3 的结果对于 G1 组来说，PP 为（0.84±0.20），时空立方体为（0.79±0.31），PP 为（0.82±0.21），时空立方体为（0.74±0.32）。 G2组的时间立方体。 PP 的 0.10 和 0.16 的非常小的效应量证实了这一点。可以推断，即使用户不熟悉 3D 可视化，也能够正确解释数据并完成简单但通用的任务。

完成任务 T1-3 后，我们要求参与者提供有关 PP 某些特性的定性反馈（回想表 1），同样按照 11 分李克特量表进行评分。 PP 的环形时间编码被评为有用 (8.07 ± 1.67) 且易于解释 (7.80 ± 1.90)。参与者认为无缝过渡是有用的 (7.47 ± 2.17) 和可解释的 (7.00 ± 2.90)。他们还表示，无缝过渡支持数据探索 (7.33 ± 1.95) 和对时间背景的理解 (7.80 ± 1.97)。参与者进一步报告说，“交互/视图转换看起来非常直观”，并且“树木年轮的隐喻让我们很容易记住时间维度”。当被问及他们喜欢的功能时，他们回答“能够旋转它们并看到无缝过渡！这可以更好地理解数据的时间维度”。他们进一步认为PP“观看起来很有趣”并提供“有趣的可能性”。当被问及其他应用场景时，与会者提到PP可以用于“行人计数、运动数据”、“心电图、脑电图、股票数据实时可视化”以及“PP可以应用于任何类型的数据测量” 。

7 讨论

PP 提供了一种以 3D 方式可视化时态数据的新技术。我们可以证明，通过 PP，我们完全能够根据自变量时间探索因变量。属性值的连续和突然变化都清晰可见。通过采用椭圆体模型进行渲染，我们可以在一个视图中显示数据，而时间就是交互的问题。

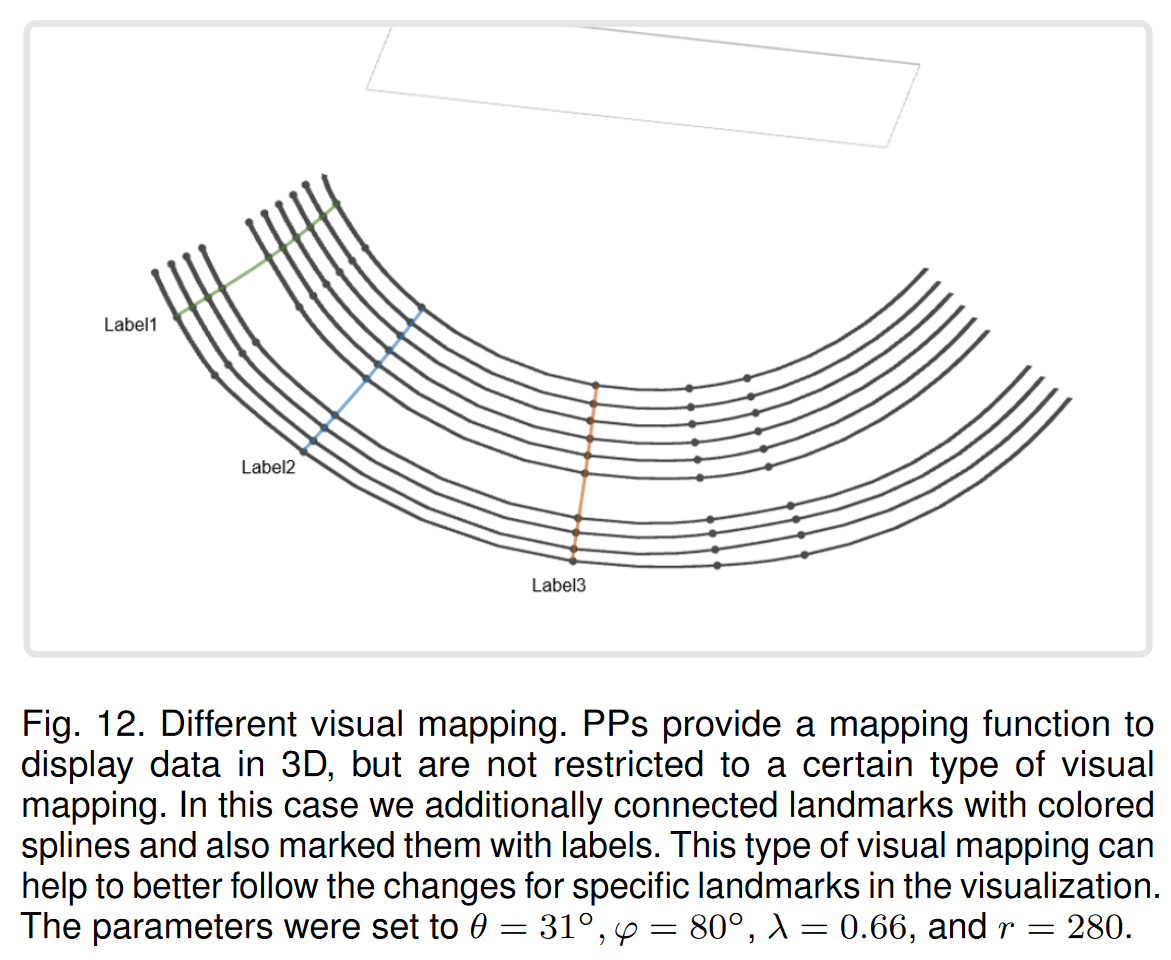
基于这种新方法，可以应用不同的现有视觉映射技术来增强视觉印象并帮助用户分析数据。在本文中，我们将数据点渲染为球体，并用样条线连接具有相同时间戳的数据点。根据应用程序领域，其他可视化技术可能更合适。为了说明这一点，我们测试了另一种类型的视觉映射，其中我们还使用样条线连接了相同地标的数据点（参见图 12）。我们还可以想象包含特定领域知识的方法，例如，在医疗用例中，可以通过 2D 切片图像来丰富 PP。特定领域的知识还可以包括突出显示时间和属性的关键阈值。

我们的方法也有一些局限性。首先，PP 仅限于 3D 数据集，其中一维类似于时间。在时空数据的某些配置中[30]，例如，当将地理地图作为两个依赖属性时，我们的方法可能不像令人满意的视觉表示。因此，我们的方法不适用于完整分析这些数据。

其次，目前并程的输入数据必须具有一定的结构。数据需要完整，具有所有时间戳中每个地标的属性值。在某些应用中，情况可能并非如此，例如，由于传感器数据丢失。这个问题可以通过在数据点之间进行插值来解决，并在可视化中直观地突出显示这些插值。还假设类似于空间（地标）的数据维度是离散的。如果空间是连续的，PP 必须以 3D 方式显示表面。我们在论文中没有遇到这样的数据集，但这是未来探索的一个有趣的方向。

第三，人类只能评估屏幕上的一定量的信息。与平行坐标 [52] 或图形 [53] 等其他可视化技术类似，如果必须显示大量数据，PP 可能会变得混乱。由于视觉混乱是可视化中的一个突出主题[54]，其解决方案可以直接转移到 PP 以增强其视觉表示。为了证明这一点，图 13 展示了使用 PP 渲染的大型数据集，其中通过根据时间更改样条线的不透明度来强调一些时间戳。我们使用具有 120 个时间戳的数据集来渲染 PP，参数设置为 λ = 0.34 和 r = 420。一个有趣的挑战是根据观看方向正确调整杂波减少技术，因为它们在观看时可能不适合沿另一个轴的数据。或者，可以使用聚类或数据降维等预处理步骤来减少要显示的数据量。

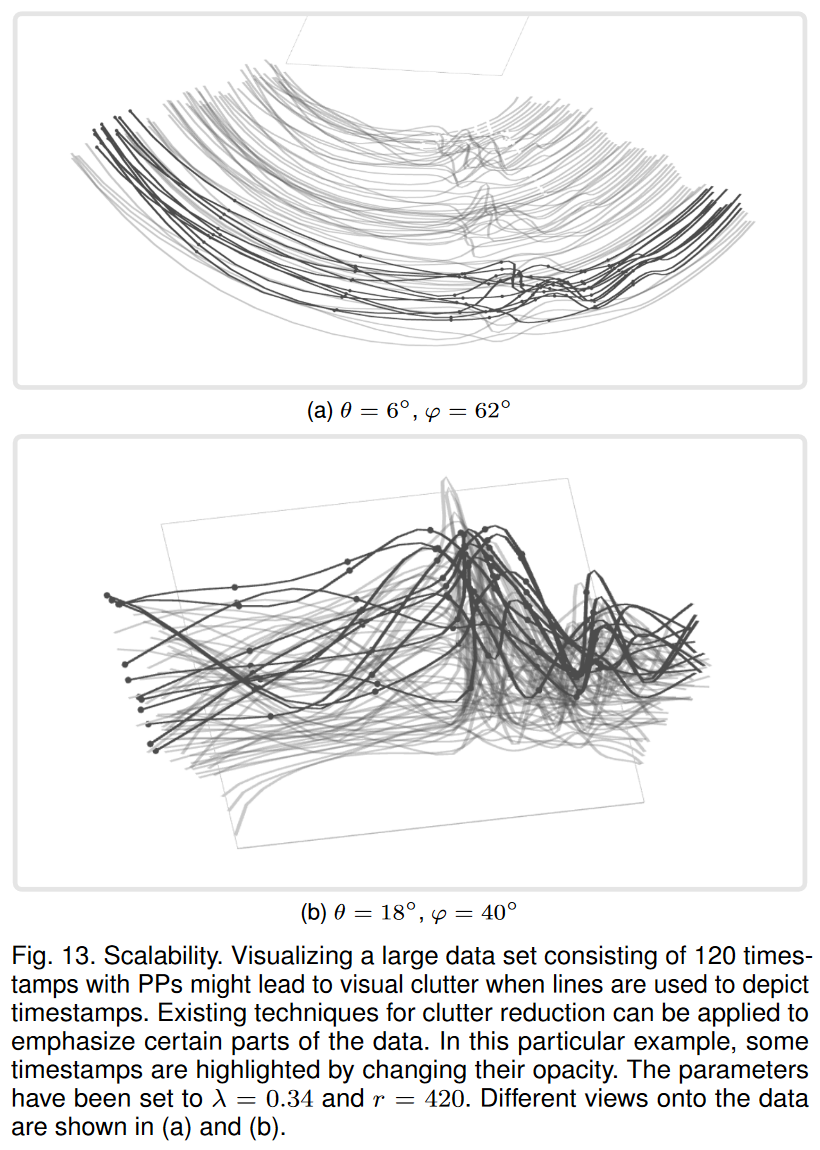
PP 提供不同数据视图之间的无缝转换。尽管这些转换可能会给熟悉新可视化技术的用户带来额外的认知负担，但用户研究中 T1 的结果表明，无缝转换很容易被用户理解。另一方面，PP 概念使用户能够在单一视图中分析数据。从这个意义上说，PP 使用户免于保留对数据的几种不同视图的概述以及正确解释刷动和链接技术的额外负担。

8 结论和未来工作

在本文中，我们提出了弹出图 (PP)，这是一种可视化包含两个因变量和自变量时间的 3D 数据集的方法。在这种情况下，两个因变量被映射到地标和属性，其中属性是特定于域的测量，而地标与空间位置相关。 PP 形成了一种新颖的映射技术，可以在三个维度上可视化数据。 PP 通过使用椭球模型弯曲空间，将传统的二维空间图和属性扩展到时间维度。时间的可视化是一个交互问题，由用户指定的 3D 旋转控制。根据 PP 的观察方向，可以研究数据的不同方面。椭球模型保证旋转过程中的平滑过渡。我们将我们的技术应用于医学和交通分析的两个数据集，以评估我们方法的多功能性。

对于未来的工作，我们希望增强我们方法的数据分析功能。不同的视角可用于研究数据的不同方面（例如，θ = 0°、φ = 0° 显示时间戳）。将来，我们希望自动从数据中提取预定义的查看方向，这可能会让用户感兴趣，因为它们显示了数据中的某些模式。这需要评估 3D 数据集的模式识别算法，并估计这些模式最可见的观看方向。模式也可以从绘图的拓扑中得出，这与 Lukasczyk 等人的工作类似。 [55]，他使用 Reeb 图的拓扑来检测轨迹数据中的热点。 PP 的可视化会受到两个参数 λ 和 r 的影响。这些参数能够可视化具有不同时间粒度的数据集。将来，研究自动查找给定数据集的最佳参数值的技术将会很有趣。

致谢

医疗数据集由斯坦福大学医学院提供，交通数据集由 AIT Austrian Institute of Technology GmbH 提供。作者感谢 Rosa Mistelbauer 对发展 PP 概念理论的支持。

参考文献